基于差分表的Blow-CAST-Fish算法的密钥恢复攻击
孙晓玲,李姗姗,杨光,杨秋格
(防灾科技学院信息工程学院,河北三河 065201)
0 引言
Feistel 密码结构是一种高效的对称结构,被广泛应用于分组密码算法的设计,对该结构的攻击方法也被广泛研究,差分分析是最经典的一种。差分分析是一种选择明文攻击,通过分析特定明文差分对相应密文差分的影响来获得最大可能的密钥。通过算法分析最终获取密钥的方法也称为密钥恢复攻击。
Blow-CAST-Fish 算法[1]是一种Feistel 结构的对称加密算法,结合了Blowfish[2]和CAST-128(C.Adams S.Tavares-128)[3]两种算法的优点,算法实现简单快速,且安全性更强。使用了基于密钥的S 盒、基于轮数的轮函数和基于子密钥的循环移位操作,使算法具有强大的抗线性分析和差分分析的能力。S 盒由密钥产生,使得算法分析更加困难,目前对该类算法的分析方法较少。研究针对该算法的攻击方法,可对算法安全性进行分析并实现密钥恢复过程,有助于精研对此类Feistel 结构密码算法的攻击方法,具有一定的理论意义和应用价值。文献[4]中分别根据单个活性S 盒和两个活性S盒的差分特征给出了Blowfish 算法的密钥恢复攻击;文献[5]中根据轮函数f1和f3的差分特性,构造了CAST-128 的6轮差分特征,并给出了8 轮算法的差分攻击方法;文献[6]中根据两个活性S 盒的差分特征,构造了Blow-CAST-Fish 算法的6 轮差分特征,并对8 轮算法进行了攻击;文献[7]中根据单个活性S 盒的差分特征,构造了Blow-CAST-Fish 算法的14轮差分特征,并对16 轮算法进行了攻击;文献[8]中提出了一种利用差分表对CAST-128 进行攻击的方法,该方法通过事先计算轮函数的差分表,根据算法输出与轮函数输入差分和输出差分的关系,计算轮密钥的值,该方法大幅降低了攻击的时间复杂度;文献[9]中基于32 轮差分特征对36 轮CAST-256 算法进行了差分攻击;文献[10]中利用积分区分器对29 轮CAST-256 算法进行了密钥恢复攻击;文献[11]中利用积分分析与零相关分析两种方法之间的联系,实现了28 轮CAST-256 算法的积分分析;文献[12]中对Type-1 广义Feistel 结构进行研究,给出了改进的多项式时间量子区分器,给出了19 轮CAST-256 的量子密钥恢复攻击。
除了经典的差分分析和线性分析,近几年出现了很多新的密码分析方法。文献[13]中提出了一种新的统计积分区分器,成功地攻击了Skipjack-BABABABA(B:Rule B,A:Rule A)的全轮密码;文献[14]中通过构建相关密钥不可能差分区分器对Deoxys 算法进行攻击;文献[15]中给出了一种在单一密钥模式下构建调柄密钥差分区分器方法对CRAFT(with effiCient pRotection Against differential Fault analysis aTtacks)算法进行密钥恢复攻击的方法。近几年,量子计算环境下的对称密码安全性研究成为热点,出现了一些针对Feistel 结构的分析成果:文献[16]中构造了一个针对4 轮Feistel 结构的量子区分器;文献[17]和文献[18]中对Feistel 结构构造了一些量子密钥恢复攻击;文献[19]中给出了广义Feistel 结构的量子区分器和密钥恢复攻击方法。
针对Blow-CAST-Fish 的攻击,文献[6-7]中采用传统的差分攻击,在构造的n轮差分特征基础上,最多只能扩充2 轮进行密钥恢复攻击,且时间复杂度和数据复杂度较高。本文利用文献[8]中查找差分表的方法,对Blow-CAST-Fish 的差分攻击进行了改进。该攻击在构造的n轮差分特征基础上,可继续扩充3 轮实现密钥恢复,与传统攻击相比,在相同差分特征下,增加了攻击轮数,且时间复杂度和数据复杂度大幅减少,提高了攻击的效率。
文献[6]中,构造6 轮差分特征,实现了8 轮算法的攻击,差分特征概率为2-61,弱密钥比例为2-12,时间复杂度为2107.9次8 轮加密,数据复杂度为264个选择明文。本文基于此6 轮差分特征,继续扩充3 轮,实现了9 轮Blow-CAST-Fish 的差分攻击,增加了1 轮攻击轮数,差分特征概率为2-61,弱密钥比例为2-12,时间复杂度降为274次9 轮加密,数据复杂度为264个选择明文。
文献[7]中,构造14 轮差分特征,实现了16 轮算法的攻击,差分特征概率为2-49,弱密钥比例为2-52.4,时间复杂度为260次16 轮加密,数据复杂度为254个选择明文。本文基于文献[7]中的2 轮差分特征,构造12 轮差分特征,在此基础上扩充3 轮,实现了15 轮Blow-CAST-Fish 的密钥恢复攻击,攻击轮数减少1 轮,差分特征概率提高至2-42,弱密钥比例增加至2-42,时间复杂度为266.1次15 轮加密,数据复杂度降为247个选择明文。
两种情况下,新的攻击与已有攻击相比,攻击效率明显提高。将本文中所使用的基于“查询差分表”的攻击与传统差分攻击对CAST 类算法的攻击结果做比较,如表1 所示。

表1 CAST类算法攻击方案对比Tab.1 Comparison of attack schemes for CAST algorithms
1 背景知识
1.1 Blow-CAST-Fish算法
Blow-CAST-Fish 算法是一种Feistel 结构的分组加密算法,输入64 bit 明文,经过16 轮迭代运算,输出64 bit 密文。初始密钥长度可变,范围为32~448 bit,由初始密钥通过密钥扩展算法生成18 个32 bit 的子密钥P1,P2,…,P18(称为P 盒)和4 个8 × 32 的S 盒S1、S2、S3、S4,S 盒的输入为8 bit,输出为32 bit,S 盒运算为查表运算。每轮运算包括P 盒的异或运算和轮函数f运算,轮函数f的核心为S 盒。算法分析过程与密钥扩展算法无关,故此处不对密钥扩展做详细介绍。
算法加密过程为:将64 bit 明文分为左、右两部分,记为(L0,R0),根据如下规则计算(Li,Ri)(1 ≤i≤16):
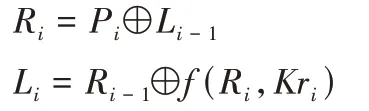
设密文C=(CL,CR),CL=R16⊕P18,CR=L16⊕P17。
函数f与轮数有关,第1、4、7、10、13、16 轮为f1,第2、5、8、11、14 轮为f2,第3、6、9、12、15 轮为f3。f1、f2和f3描述如下:

其中:“<<<”表示循环左移操作,“⊕”表示异或运算,“-”表示模232减法运算,“+”表示模232加法运算,“‖”为连接符,F为f的部分操作。I为32 bit 数据,由高位到低位分成4 个字节,分别为Ia、Ib、Ic、Id。Si[It]表示对S 盒Si进行查表运算,输入为It,输出为Si[It]。
算法加密流程如图1 所示。

图1 Blow-CAST-Fish算法的加密流程Fig.1 Encryption flow of Blow-CAST-Fish algorithm
1.2 差分分析
以下知识介绍中的S 盒和差分特征以Blow-CAST-Fish算法为例。S 盒的输入为8 bit,输出为32 bit。
S 盒的碰撞性 若S 盒存在一对输入,其差分值等于γ(γ是一个字节,γ≠0),经过S 盒变换后,输出差分值为0000(0000 是4 个字节),则称S 盒存在碰撞γ→0000。存在碰撞的S 盒称为活性S 盒。
S 盒的碰撞概率 若S 盒共有M对不相等的输入,其中m对满足输入差分为γ、输出差分为0000,则S 盒存在碰撞γ→0000 的概率为m/M。
单轮差分特征及特征概率 首先将S 盒的碰撞性扩展到整个F函数,假设只有S1存在碰撞γ→0000,概率为p,可构造F函数的输入差分为γ000、输出差分为0000 的差分特征,概率为p。继而扩展到整轮,可构造输入差分为γ000>>>Kri(Kri为本轮循环左移密钥)、输出差分为0000 的差分特征,概率为p。此时单轮差分特征概率只与输入、输出差分有关,概率为活性S 盒的碰撞概率。
n轮差分特征 选取合适的输入差分,可以在单轮差分特征的基础上扩展到n轮差分特征。选取明文输入差分为0000‖(γ000 >>>Kr2)。第1 轮左半部分输入差分为0000、输出差分一定为0000,概率为1;第2 轮左半部分输入差分为γ000 >>>Kr2,经过密钥加密和左移,F函数的输入差分为γ000,输出差分为0000,概率为p;第3 轮与第1 轮相同;第4轮左半部分输入差分为γ000 >>>Kr2,经过密钥加密和左移,F函数的输入差分为(γ000 >>>Kr2)<<<Kr4,差分特征(γ000 >>>Kr2)<<<Kr4→0000 是否存在与Kr2、Kr4有关,特征概率与活性S 盒的碰撞概率相同,只与活性S 盒的输入、输出差分有关。后续轮数与前面类似。
n轮差分特征概率 等于每轮特征概率的乘积。
弱密钥 使得碰撞存在,即使得上述构造的差分特征存在的密钥称为弱密钥。弱密钥存在,则差分特征可构造。
正确对 对于由n轮差分特征扩展而来的攻击过程,随机选择明文,满足给定输入差分和对应输出差分的明文对,称为正确对。假设n轮差分特征概率为2v,攻击选取的明文对数量为2w,则正确对的个数为2v× 2w。由正确对分析出来的密钥即为正确密钥。对于输入明文长度为64 bit 的Blow-CAST-Fish 算法,可选明文对最多有263对,故可用于攻击的差分特征概率不能低于2-63。
1.3 攻击效率
评价攻击效率,主要从攻击轮数、弱密钥比例、代价这3个方面综合分析。对于Blow-CAST-Fish 算法,首先考虑两个S 盒的碰撞性,两个S 盒的输入、输出是16 bit 到32 bit 的映射,碰撞概率较高,故弱密钥比例很高,但差分特征概率较低,最多可构造特征概率为2-61的6 轮差分特征,因为如果轮数再多,差分特征概率将低于2-63,在明文空间为264的情况下,将不存在正确对,攻击无法实现,所以基于两个S 盒的碰撞,最多构造6 轮差分特征,用本文攻击方法最多可实现9 轮攻击,比已有攻击多了1 轮,且降低了时间复杂度。为了增加攻击轮数,考虑单个S 盒的碰撞性,单个S 盒是8 bit 到32 bit 的映射,碰撞概率较低,故弱密钥比例很低,但差分特征概率较高,可构造特征概率为2-49的14 轮差分特征,但本文攻击方法可在已构造差分特征的基础上扩充3 轮,而Blow-CAST-Fish 算法共有16 轮,所以本文选择构造特征概率为2-42的12 轮差分特征,在此基础上可实现15 轮算法的攻击,与已有攻击相比,总攻击轮数减少了1 轮,但同样基于12轮差分特征,攻击轮数还是增加了1 轮,攻击的总代价相对有所降低。两种情况相比,基于的活性S 盒个数不同,导致特征概率和弱密钥比例不同,可攻击轮数也不同。9 轮攻击基于多个活性S 盒,特征概率低,可攻击轮数有限,但弱密钥比例很高;15 轮攻击基于单个活性S 盒,特征概率高,可攻击轮数多,但与9 轮攻击相比,弱密钥比例很低。两种攻击,各有优缺点,具有不同的理论意义。
2 9轮Blow-CAST-Fish的密钥恢复攻击
2.1 6轮差分特征
假设F函数已知,即4 个S 盒的值已知。文献[6]中给出了基于两个S 盒的碰撞性构造的Blow-CAST-Fish 的6 轮差分特征:
映射(Ia,Ib)→S1[Ia]-S2[Ib]是一个16 bit 到32 bit 的映射函数,以较高的概率存在碰撞,即存在输入(Ia,Ib)、(Ia',Ib'),使得(S1[Ia]-S2[Ib])⊕(S1[Ia']-S2[Ib'])=0。设δ=Ia⊕Ia'、μ=Ib⊕Ib',假设S1-S2只存在一对输入满足输入差分为δμ、输出差分为0000(δμ为16 bit 数值、0000 为32 bit 数值),则该碰撞的概率为2-15。可构造第2 轮中F函数的输入差分为δ μ00、输出差分为0000 的差分特征(δ μ00、0000 为32 bit 数据),进而可构造Blow-CAST-Fish 的2 轮差分特征,如下所示:

在此基础上,可扩展到整个6 轮差分特征为:

其中:>>>为循环右移;‖连接左、右两半部分差分值;Kr2为第2 轮循环左移密钥,取值任意;p为当前轮的差分特征概率。此6 轮差分特征概率为2-61、弱密钥比例为2-12,如图2所示。

图2 6轮差分特征Fig.2 Six-round differential characteristics
弱密钥比例测试方法参见文献[6],任选5 个随机密钥及其产生碰撞的一种情况作为示例,如表2 所示,表中初始密钥为字符形式,S 盒的输入、输出均为十六进制形式,用下标x表示。

表2 S1 - S2碰撞情况示例Tab.2 Examples of S1 - S2 collision
2.2 9轮算法的密钥恢复过程
为了提高攻击效率,为f3预先计算一个差分表,即为所有输入、输出差分组合创建一个表,用于存储具有相同输入、输出差分的输入-输出对,例如,设a、b为f3的2 个32 bit 输入,输入差分ΔIn=a⊕b,输出差分ΔOut=f3(a)⊕f3(b),则将(a,f3(a))存储在表中ΔIn→ΔOut对应的条目处。在F函数已知的情况下,考虑Kri共有25种取值,需计算32 个表,记作Tj(j=0,1,…,31)。由于f3的输入、输出均为32 bit,所以共有264种输入、输出差分组合和232× 232种输入-输出对,故对于固定的输入、输出差分组合,平均可以找到一个对应的输入-输出对。
下面利用差分表实现9 轮算法攻击。首先在6 轮差分特征的基础上,将算法轮数扩充到9 轮,如图3 所示,设第i轮的输入为(Li-1,Ri-1),输出(Li,Ri)为下一轮的输入,第9 轮中,轮函数f3的输入记为X9,输出记为Y9,对明文进行9 轮加密后的密文记为(CL,CR),“????”表示数值不确定。
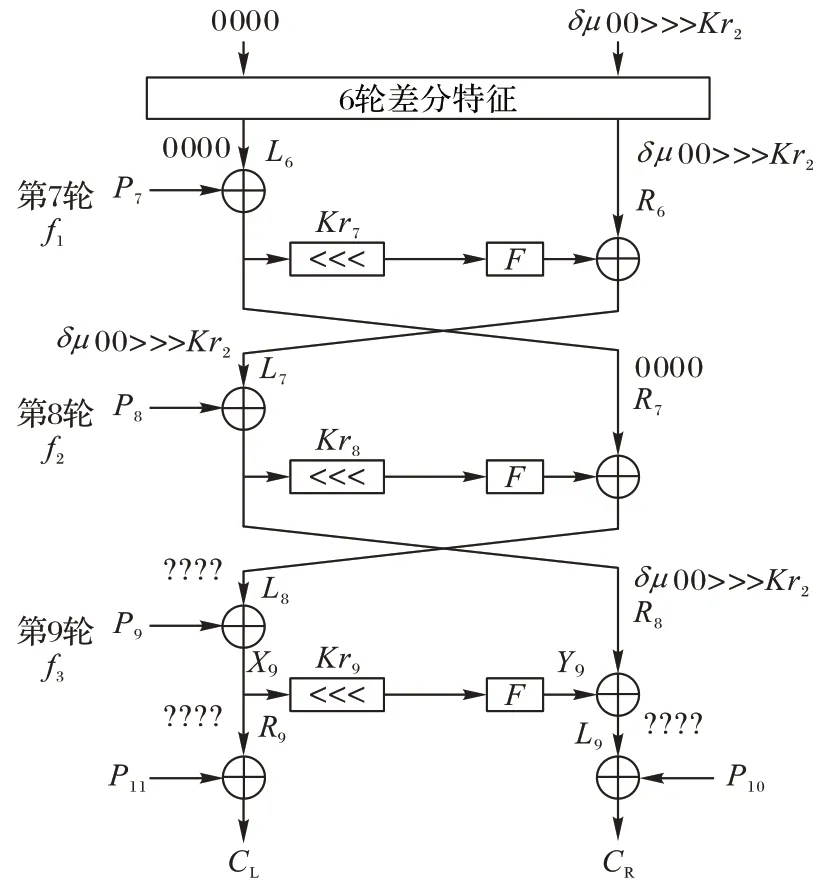
图3 9轮Blow-CAST-Fish算法的差分攻击过程Fig.3 Flow of differential attack of 9-round Blow-CAST-Fish algorithm
具体攻击过程如下:
1)循环Kr2的25个值。数据采集阶段,选取232个结构,每个结构包含232个具有相同左半部分的明文。为满足明文差分为0000‖(δμ00 >>>Kr2),每个结构可产生231个明文对,一共可得263个明文对,对这些明文进行9 轮加密,可得263个密文对。
2)循环Kr9的25个值,设置计数器数组V[232]并将其初始化为零。
3)循环263个密文对,可以计算第9 轮中轮函数f3的输入异或差分和输出异或差分:
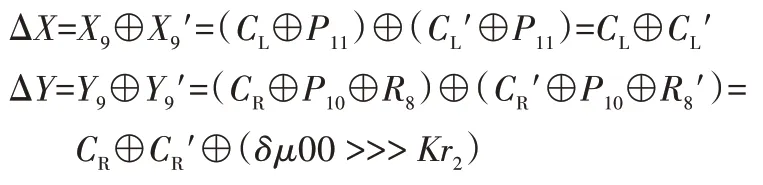
查找对应的差分表T,得到(X9,Y9)和(X9',Y9'),计算P11=CL⊕X9。将计数器V[P11]加1。
4)将数值最大的计数器所对应的(Kr2,Kr9,P11)的值保存下来,这些值即为正确密钥。
将整个密钥恢复过程更加简洁地进行归纳,如算法1所示。
算法1 9 轮Blow-CAST-Fish 算法的密钥恢复过程。

2.3 复杂度分析
首先计算此次差分分析的信噪比,信噪比的计算公式为:

其中:p为差分特征概率,k为所恢复密钥的比特数,α为分析每对消息时的密钥计数,β为分析的消息对占总消息对的比例。本次攻击中,p=2-61,所恢复密钥为Kr2、Kr9、P11,总长度为42 bit,所以k=42,分析每对消息时,Kr2、Kr9取值是遍历的,故α=210,因为用于分析的消息对要满足异或值为0000‖(δ μ00 >>>Kr2),故β=2-32。

攻击成功的概率由如下公式计算:

k=42,τ是正确对的个数,本文攻击中,τ=232×231×2-61=22,故Ps=0.999,攻击成功的概率接近于1。
数据复杂度 攻击过程中,选择了232× 232个明文,故数据复杂度为264个选择明文。
时间复杂度 首先,预生成了32 个差分表,每个表的生成过程中,需遍历所有输入-输出对,时间复杂度为32 ×232× 232× 2=270次一轮加密,等于270/9 ≈266.9次9 轮加密;其次,密钥恢复过程中,为每个Kr2的取值选取263对异或值等于0000‖(δμ00 >>>Kr2)的明文对,其时间复杂度为25×263× 2=269次9 轮加密,第9 轮密钥恢复过程中,用到了25×25× 263× 2=274次查表,假设一次查表操作等价于一次9 轮加密,则密钥恢复的时间复杂度为274次9 轮加密。故总的时间复杂度为266.9+268+274≈274次9 轮加密。
空间复杂度 差分表所占存储空间总共为32 × 264×8=272字节,密钥恢复过程的空间复杂度为计数器和密钥所占空间,约为232字节,总的存储空间为272+232≈272字节。
构造差分特征的时间和空间复杂度 构造差分特征即测试是否存在弱密钥使S 盒具有碰撞性,碰撞发生在第2、4、6 轮,每轮测试随机选取210个初始密钥。第2 轮有两个活性S 盒,总共进行210× 28× 28× 28× 28=242次S 盒查表运算,一次9 轮加密总共有4 × 9=36 ≈25次S 盒运算(其他异或运算耗时忽略不计),则总的时间复杂度约为237次9 轮加密。第4 轮和第6 轮,活性S 盒不固定,但无论密钥取何值,一定有一个S 盒是非活性的,所以要测试3 个S 盒的碰撞,因为输入差分固定且与循环密钥Kri有关,则总共进行210× 232×25× 6 ≈250次S 盒查表运算,相当于245次9 轮加密。3 轮总的时间复杂度为237+245+245≈246次9 轮加密。空间复杂度为4 个S 盒的存储空间和一个密钥(32~442 bit)的存储空间,总共为4 × 28× 4+112 ≈212字节。
3 15轮Blow-CAST-Fish的密钥恢复攻击
3.1 12轮差分特征
文献[7]中,在假设F函数已知的情况下,为提高差分特征的概率,以增加攻击轮数,只考虑单个活性S 盒的情况。以S1为研究对象,考虑映射Ia→S1[Ia](Ia为8 bit),假设S1存在碰撞,即存在两个不同的字节Ia和Ia',使得S1[Ia]=S1[Ia']。假设满足碰撞的输入只有一对,则碰撞概率为2-7。设δ=Ia⊕Ia',Kr2为第2 轮的循环左移密钥,取0~31 的任意值,构造了如下所示的2 轮差分特征,其中“0000”,“δ000 >>>kr2”分别表示明文左右两半部分的32 位异或差分值,>>>表示循环右移,p为当前轮的差分特征概率。
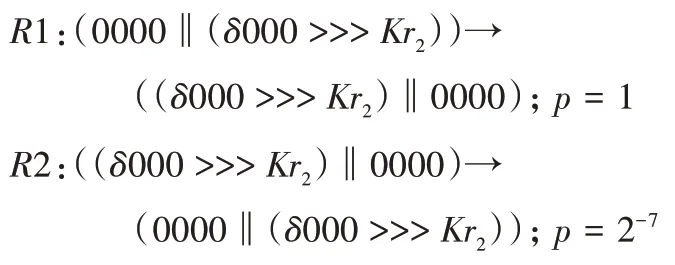
假设Kr4=Kr6=Kr8=Kr10=Kr12=Kr2,将上述2 轮差分特征重复6 次,可构造12 轮差分特征,如图4 所示。前12 轮差分特征概率为2-42,弱密钥比例为2-42。
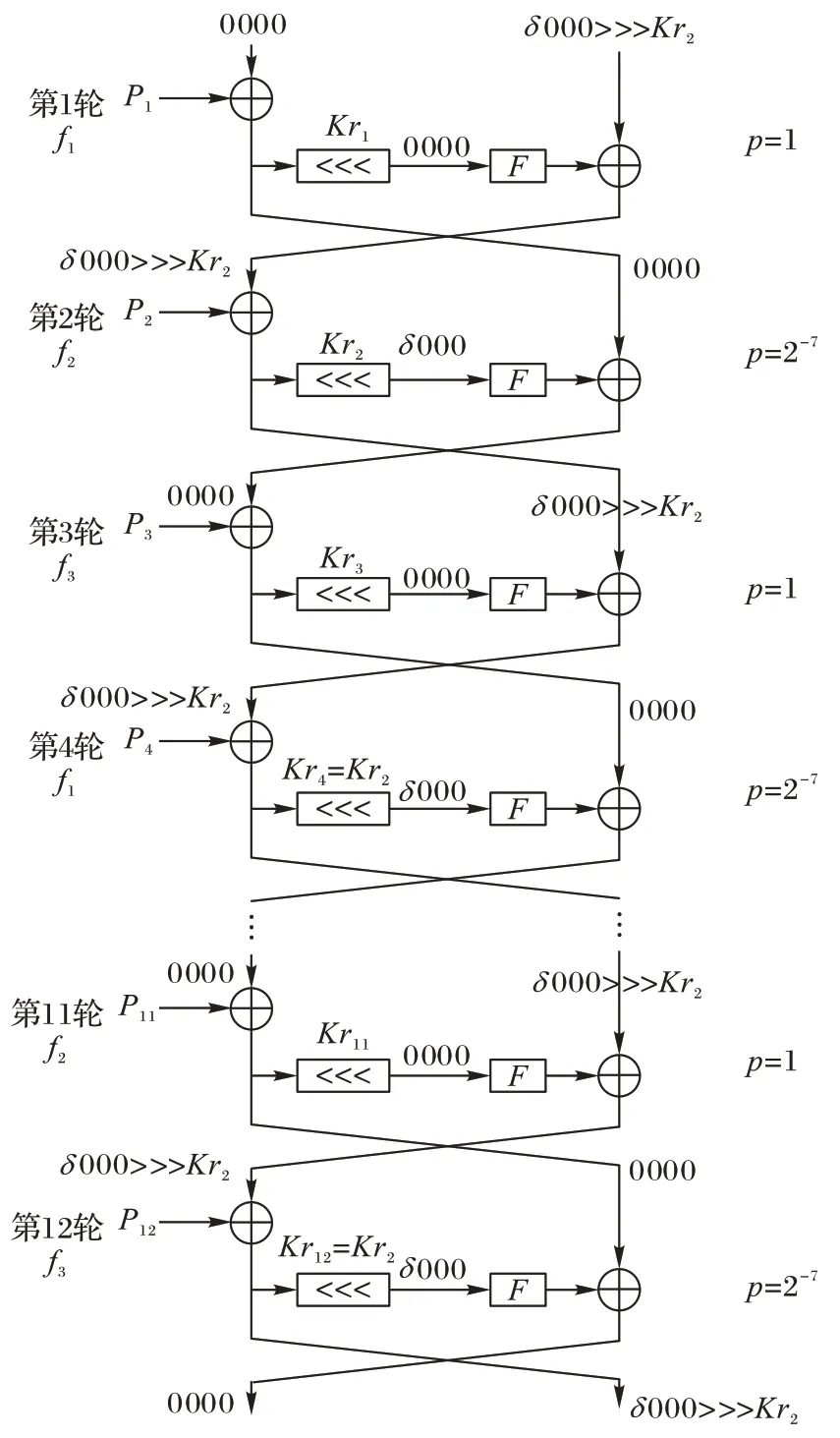
图4 十二轮差分特征Fig.4 Twelve-round differential characteristics
弱密钥比例测试方法参见文献[7],表3 为一轮测试10万个随机初始密钥中弱密钥及使S1产生碰撞的情况,表中初始密钥为字符形式,S 盒的输入、输出均为十六进制形式,用下标x表示。

表3 S1碰撞情况示例Tab.3 Examples of S1 collision
3.2 15轮算法的密钥恢复过程
用前面所述同样的方法为f3建立差分表,下面利用差分表实现15 轮算法的密钥恢复攻击。
首先在12 轮差分特征的基础上,将算法轮数扩充到15轮,如图5 所示,设第i轮的输入为(Li-1,Ri-1),输出(Li,Ri)为下一轮的输入,第15 轮中,轮函数f3的输入记为X15,输出记为Y15,对明文进行15 轮加密后的密文记为(CL,CR),“????”表示数值不确定。

图5 15轮Blow-CAST-Fish算法的差分攻击过程Fig.5 Flow of differential attack of 15-round Blow-CAST-Fish algorithm
具体攻击过程如下:
1)循环Kr2的25个值。数据采集阶段,选取215个结构,每个结构包含232个具有相同左半部分的明文。为满足明文差分为0000‖(δ000 >>>Kr2),每个结构可产生231个明文对,一共可得246个明文对,对这些明文进行15 轮加密,可得246个密文对。
2)循环Kr15的25个值,设置计数器数组V[232]并初始化为零。
3)循环246个密文对,可以计算第15 轮中轮函数f3的输入异或差分和输出异或差分:

查找对应的差分表T,得到(X15,Y15)和(X15',Y15'),计算P17=CL⊕X15。将计数器V[P17]加1。
4)将数值最大的计数器所对应的(Kr2,Kr15,P17)的值保存下来,这些值即为正确密钥。
将整个密钥恢复过程进行归纳,如算法2 所示。
算法2 15 轮Blow-CAST-Fish 的密钥恢复过程。


3.3 复杂度分析
首先计算此次差分分析的信噪比。本次攻击中,p=2-42,所恢复密钥为Kr2、Kr15、P17,总长度为42 bit,所以k=42,分析每对消息时,Kr2,Kr15取值是遍历的,故α=210,因为用于分析的消息对要满足异或值为0000‖(δ000>>>Kr2),故β=2-32。

攻击成功的概率由如下公式计算:

k=42,τ是正确对的个数,本文攻击中,τ=215×231×2-42=24,故Ps=0.999,攻击成功的概率接近于1。
数据复杂度 攻击过程中,选择了232×215个明文,故数据复杂度为247个选择明文。
时间复杂度 首先,预生成了32 个差分表,每个表的生成过程中,需遍历所有输入、输出对,时间复杂度为32 ×232× 232× 2=270次一轮加密,等于270/15 ≈266.1次15 轮加密。其次,密钥恢复过程中,为每个Kr2的取值选取246对异或值等于0000‖(δ000 >>>Kr2)的明文对,其时间复杂度为25× 246× 2=252次15 轮加密,第15 轮密钥恢复过程中,用到了25× 25× 246× 2=257次查表,假设一次查表操作等价于一次15 轮加密,则密钥恢复的时间复杂度为257次15 轮加密。故总的时间复杂度为266.1+252+257≈266.1次15 轮加密。
空间复杂度 差分表所占存储空间总共为32 × 264×8=272字节,密钥恢复过程的空间复杂度为计数器和密钥所占空间,约为232字节,总的存储空间为272+232=272字节。
构造差分特征的时间和空间复杂度 碰撞发生在第2、4、6、8、10、12 轮,每轮只有S1是活性的,只需测试S1的碰撞性即可。测试的时候随机选择106个初始密钥,总共进行106× 28× 28≈235.9次S 盒查表运算,一次15 轮加密总共有4 × 15=60 ≈26次S 盒运算(其他运算时间可忽略不计),则总的时间复杂度为229.9次15 轮加密。空间复杂度为4 个S 盒的存储空间和一个密钥(32~442 bit)的存储空间,总共为4 ×28× 4+112 ≈212字节。
4 结语
本文通过为轮函数f3构建差分表,改进了Blow-CASTFish 的差分攻击,可在固定n轮差分特征的基础上,扩充3 轮进行密钥恢复攻击,可以更高的效率实现密钥恢复过程。首先,基于多个活性S 盒,构造6 轮差分特征,实现了9 轮算法的密钥恢复攻击;其次,基于单个活性S盒,构造12 轮差分特征,实现了15 轮密钥恢复攻击。两种攻击相比:9 轮攻击轮数少,但弱密钥比例很高,攻击成功概率高;15 轮攻击轮数较多,但弱密钥比例很低,攻击成功概率低。
分析结果表明,使差分特征成立的弱密钥是以一定概率存在的,故差分特征可构造,攻击在弱密钥下可成功;且构造差分特征的时间和空间复杂度相比攻击代价要小得多,不会影响攻击效果。此攻击方法为该类CAST 型Feistel 结构分组密码算法的最优攻击方案。

