Grover算法与滑块碰撞的相似性

李开玮

(广东理工学院 智能制造学院，广东 肇庆 526100)

量子搜索中，Grover算法是一个非常重要的搜索算法，相对于经典搜索算法而言，有平方加速的效果，在量子计算中，量子态处于一些基态(基矢量)的叠加态中，在运算时会同时对整个叠加态作矩阵运算，测量时只能有一定的概率得到想要的基态，Grover算法的核心是不断增大想要的基态概率幅，减小其他基态概率幅，当目标基态的概率幅接近1时，再作测量就可以精确得到搜索结果[1].对量子态作矩阵运算，其过程非常类似于滑块碰撞中的处理方法[2-3].接下来首先分析Grover算法，再比较其与滑块碰撞的相似特点.

1 Grover算法

对于n个量子比特的非结构化数据库中，有N=2n个量子基态|i〉，i=1,2,…,N，其中有一个目标态|τ〉满足黑盒(Oracle)函数f(i)=1，量子搜索算法即是以尽可能大的概率找到目标态|τ〉，Grover算法的步骤是这样的，首先制备均匀态，使每个基态的概率幅相等

(1)

然后利用Oracle识别并给目标态|τ〉标记，使|τ〉的概率幅取反，Oracle算符为：

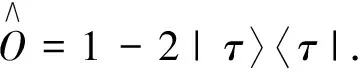
(2)

其次利用G算符将叠加态关于|φ〉翻转，使所有基态的概率幅关于概率幅均值翻转，目标态的概率幅将会增大，其他基态的概率幅减小，G算符为：

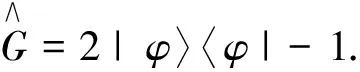
(3)

接下来重复迭代(2)、(3)若干次将会以几乎为1的概率测得目标态|τ〉.

为了方便描述，如图1所示，将非目标态加起来，将

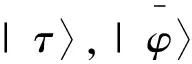
图构造的正交坐标系

(4)

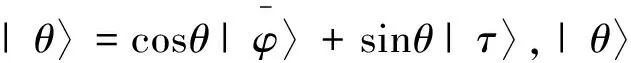
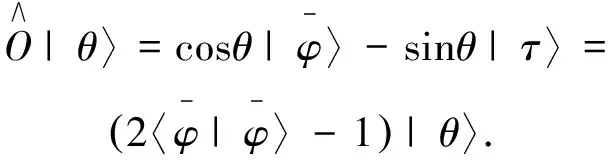
(5)

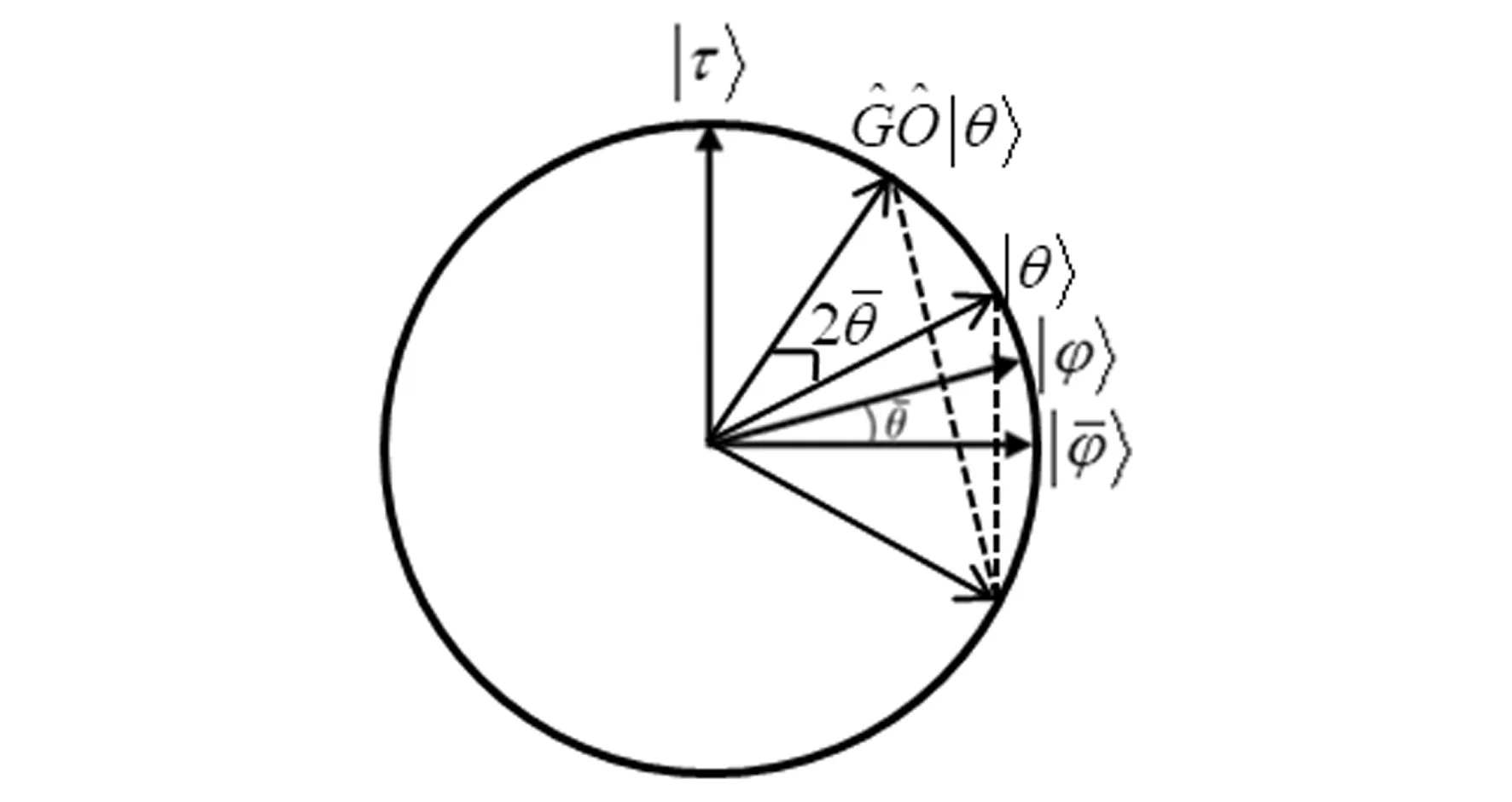
图迭代运算图像

2 与滑块碰撞的巧合

经典力学中滑块碰撞问题如如图3所示，水平光滑的地面上放置小木块m和大木块M，左端是固定的墙壁，初始时刻m静止，M以初速度v0向左运动，将与m发生碰撞，之后m获得速度向左运动，将与墙壁发生碰撞反弹，假设所有碰撞均没有能量损失，求碰撞次数.

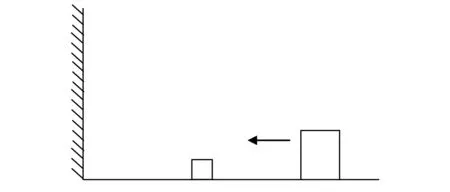
图3 滑块碰撞示意图

图4 两滑块连续碰撞速度坐标变换

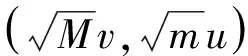
3 结语