平行度误差激光准直法测量技术研究
王红敏,罗自赢,李 蕾,彭俊玲
(1.山东理工大学 机械工程学院,淄博 255000; 2.河南科技大学 车辆与交通工程学院,洛阳 471003; 3.中国计量大学 计量测试工程学院,杭州310018; 4.燕山大学 电气工程学院,秦皇岛066004)
引 言
随着工业技术的快速发展,对几何量测量中各种几何参数的测量精度提出了越来越高的要求。其中直线度、平行度等形位误差测量是精密测量领域中关键的重要测量项目[1-2],直接影响产品质量和性能。位置敏感探测器(position sensitive device,PSD)是一种测量光点在探测器表面上连续位置的光学探测器,可将光敏面上的光点位置转化为电信号,作为非接触式传感器特别适于位置、位移、厚度等的精确动态实时检测,具有宽光谱响应范围、快响应、高分辨率、可连续检测、光敏面位置无盲区、且对光能量中心尤为敏感等优越性能,极适合动态测量[3-7],所以在激光准直、位移、角度、机器人控制等方面获得广泛应用,
激光以其亮度高、指向强、单色好、相干强、测距远、精度高等优异性能被广泛应用于多种行业领域,如激光通信、印刷、医疗、军事、工业加工等,同时激光准直技术也在精密测量领域得以深入研究[8-11],相关技术在精密测量、工程安装调试及安全监测等方面都具有重要意义和广阔前景。激光作为一种光源,离不开光波的传输,激光光学系统中的光波传输归结为高斯光束的传输,本文作者基于高斯光束的传输特性、聚焦和准直以及透镜变换规律,探讨了基于PSD的激光准直技术及其在平行度误差测量中的应用。
1 测量系统方案设计
1.1 测量基本原理
由于激光能量集中且具有较好的指向性和相干性,因此,激光束作为直线基准测量工件表面形状误差,可以消除一般传统光学方法长距离测量时像质模糊、可靠性相对较弱的缺点。激光准直法测量的基本原理如图1所示。

Fig.1 Principle of laser alignment measurement
激光器发出的光束(光束中心线作为测量的基准线)照射在PSD光靶上,当光靶沿被测表面(如机床导轨)移动时,如果被测工作表面存在形状误差,将会使光靶与激光束之间产生相对移动,激光束入射到PSD光敏面上的位置因此而发生改变,PSD将此位移量转变为电流信号,然后经信号调理,再送入单片机应用系统进行数据采集、运算、处理,即可实时显示某一点相对基准线的位置,测量结束后将数据传送给计算机,利用专用软件快速评定出被测工作表面的形状和位置误差。测量系统工作流程如图2所示,图中,I/V表电流/电压。
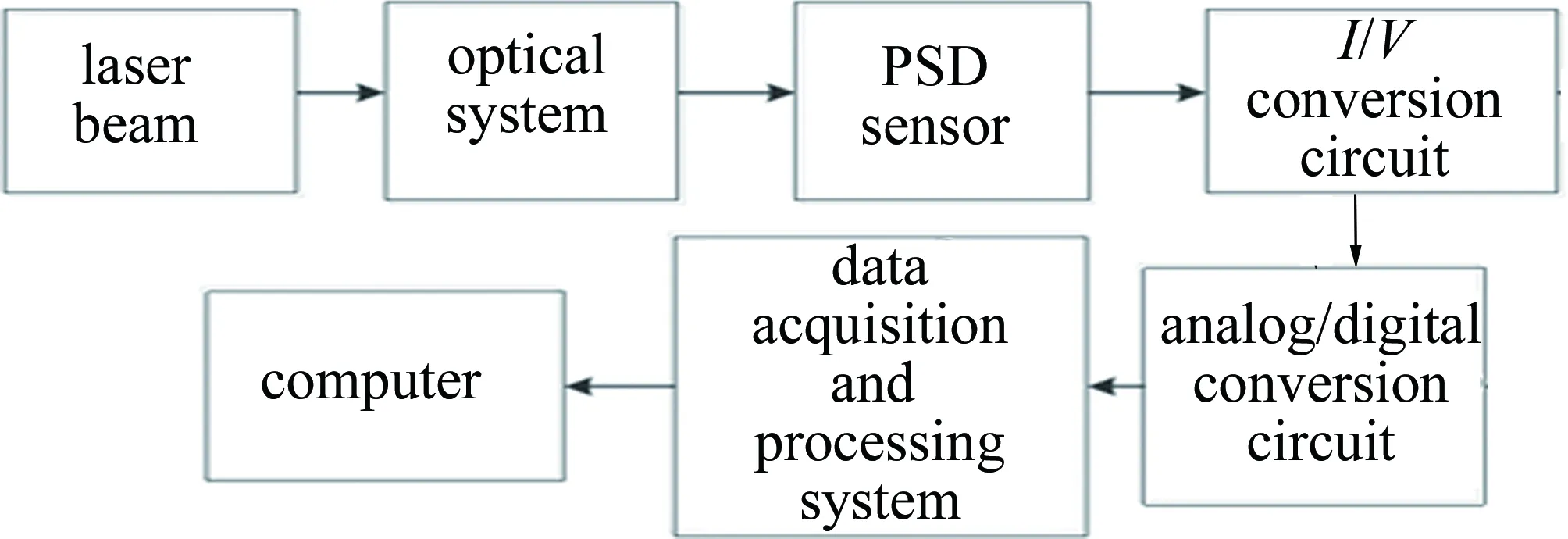
Fig.2 Flow chart of measuring system
1.2 激光准直与聚焦
根据激光衍射理论,高斯光束在匀质透明环境中沿z向传播时,其光场分布函数为[12-13]:
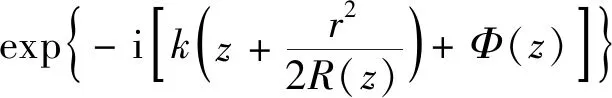
(1)
式中,c为常数因子,r2=x2+y2,w(z)、R(z)、Φ(z)分别为高斯光束在位置z处的截面半径、波面曲率半径和相位因子,它们均为高斯光束传播中的重要参数,其表达式分别为:
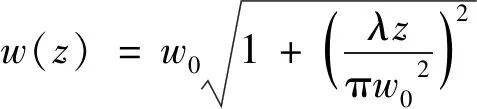
(2)

(3)

(4)
式中,w0为z=0时的截面半径,k=2π/λ为光波的波数,λ为波长。
从(1)式可以看出,高斯光束截面内的光强并非均匀分布,若位置z处的光斑截面中心振幅为A0(z),则高斯光束的振幅A(z)与参数r的函数关系可表示为:

(5)
从(5)式可知,振幅A(z)随着参数r的增加而递减,光束截面中心振幅A0(z)最大。图3所示为截面半径w(z)随传播方向z而变化的曲线。
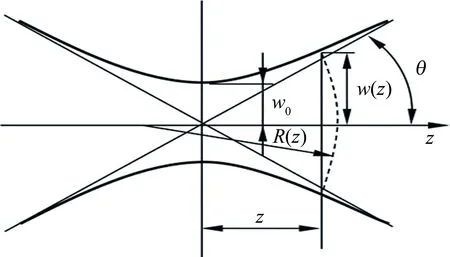
Fig.3 Propagation of Gaussian beam
图3中,w0为光束最细处的截面半径,简称高斯光束的束腰。同时还可以看出,高斯光束在传播过程中,光束的截面半径轨迹是一对双曲线,每一点的光束截面半径w(z)和波面曲率半径R(z)均不相同,其中光束发散情况用该双曲线的渐近线与z轴的夹角θ来表示,表征光束的发散情况。θ是激光光束的另一重要参量:
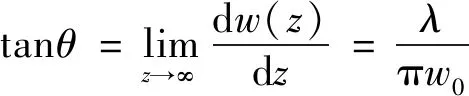
(6)
由(6)式可知,若要减小激光的发散度,则必须增大物方光束的束腰半径w0。
当高斯光束物面位于物方束腰处时,经焦距为f′的透镜变换后,像距l′和束腰半径w0′表达式分别为:
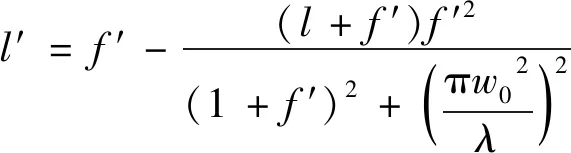
(7)

(8)
当l=-f′时,由(7)式得l′=f′,即高斯光束束腰位于透镜物方焦面时,透镜变换后束腰位于透镜像方焦面,如图4所示。此时:
w0′=f′λ/(πw0)
(9)
即l=-f′时,w0′极大,此时出射光束具有最大束腰半径。
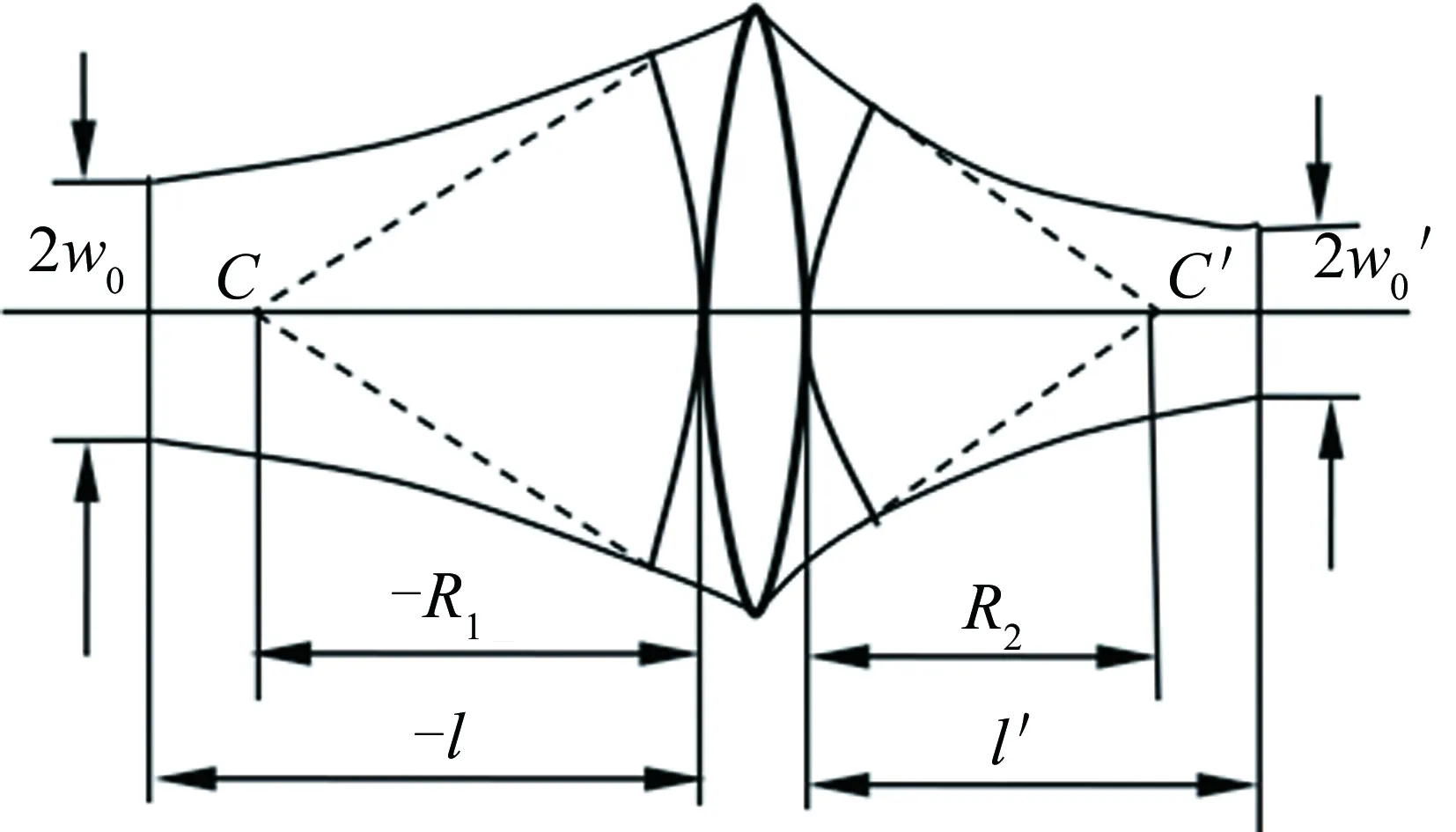
Fig.4 Lens transformation of Gaussian beam
从(9)式可知,若要求激光聚焦效果好,则需减小透镜像方焦距f′和增大物方光束的束腰半径。
高斯光束中发散角客观存在,但精密测量中为了提高其准直性,使能量不随距离增大而快速减小,就需要进一步压缩激光发散角,对高斯光束进行准直。对准直系统而言,发散角越小越好,所以准直的核心目的在于减小光束的发散角,提高方向性。因此角度很小时,由(6)式得高斯光束发散角近似为:
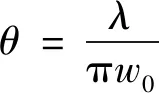
(10)
透镜变换后,

(11)
代入(8)式,可得:
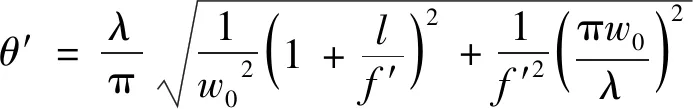
(12)
可以看出,上式中θ′≠0,即高斯光束经单透镜变换后的波面并非平面波。当l=-f′时,则得:
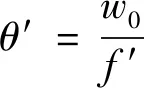
(13)
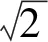
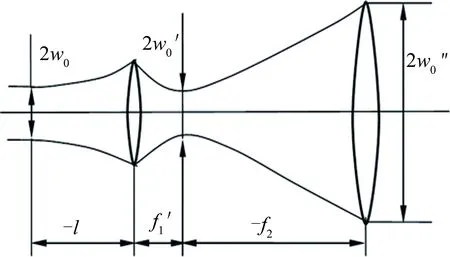
Fig.5 Collimation of Gaussian beams
1.3 PSD传感技术及应用
PSD按结构分1维和2维两种,系统选用2维PSD实时显示被测件的直角坐标x值和y值。2维PSD典型结构示意图如图6所示。

Fig.6 Schematic diagram of 2-D-PSD
当以PSD中心作为坐标原点时,电流与其位置成如下关系[4,6]:
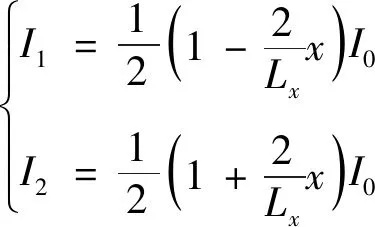
(14)
则:
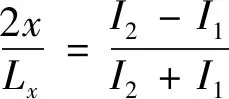
(15)
同理可得:
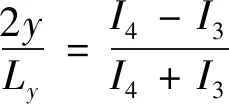
(16)
式中,x为PSD受光面上成像点水平坐标位置,y为PSD受光面上成像点垂直坐标位置;Lx、Ly分别为PSD两个方向电极之间的长度;I0为电极间总电流,I1、I2、I3、I4分别为PSD两个方向电极2维坐标位置的4路电流值。
因此,只要知道PSD的4个输出电流I1、I2、I3、I4,PSD上的成像位置坐标x值和y值可以经上述公式计算得到,从而得到PSD受光面上的成像位置。但PSD输出电流极微弱,为了便于后续处理计算,需要信号调理电路对PSD输出信号进行转换[3-7],信号处理主要是采集处理PSD所输出的代表2维坐标位置的4路电流值,将其转化为电压信号,再经模数转换变为数字信号,以便单片机进一步处理。4个采样输入端口同时采样,高速并行接口,数据传入计算机,通过专用软件对数据进行进一步评定处理。
2 实验测量系统设计
基于上述分析,设计平行度测量实验装置如图7所示。测量前先将光学五棱镜置于测量前端放正,并进行位置调整,然后将光靶沿被测表面测量方向移动,便能得到表面形状误差的原始数据。
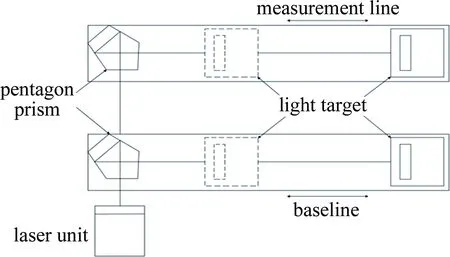
Fig.7 Design of parallelism measuring device
系统中发射装置使用650nm红光半导体激光器,激光输出1mW,匹配精密激光校准装置。接收器中的PSD位置敏感元件可以精确灵敏感应激光束,使信号处理器避免各种外界干扰,从而得到精确的测量数据。经信号处理系统得到的数据可通过接口或无线蓝牙技术传输到计算机,确保传输数据的安全和便捷。
2.1 实验技术分析
实验测量以某导轨水平方向平行度误差为例,测量时先做隔振处理和同轴调整,然后保持激光发射器位置不动,先进行基准线测量:将五角转向棱镜置于基准线前端放正,并进行位置调整,将光靶移动到转向五角棱镜近端,依次移动光靶逐段测量,直到基准线测量完成;然后重复以上步骤对被测线进行测量,测量完成后将测量数据导入软件,采用最小包容区域法评定,得出被测平行度误差。
最小包容区域法是最小条件法之一,是国家规定的误差评定的一种仲裁方法[14-15],其评定结果最小且唯一。最小包容区域法评定形状类误差如直线度误差,是先计算从目标各采样点(xi,yi)(i=1,2,…,n)到理想直线y=ax+b的纵向距离di=yi-(axi+b),据此建立目标函数F(a,b)=max{di}-min{di},当包容区最小化时,求解该二元函数的最小值,即可得到直线度误差f_。
平行度误差属位置误差范畴,采用最小包容区域法评定时,基本原理是包容实际被测要素且具有最小包容区域,并与基准要素保持平行且距离最小的两平行线或面间的距离,该两条平行线或面即为评定相关误差的包容线或面。平行度误差评定(以平行线为例)的具体方法为,通过被测要素目标各采样点(xi,yi)(i=1,2,…,n)作和理想直线y=ax+b相平行的系列平行线,然后求目标各采样点到理想直线的纵向距离li=yi-(axi+b),其中距离的最大值与最小值之差即平行度误差f∥=max{li}-min{li}。图8所示为平行度误差评定(以平行线为例)原理图。图中包含实际被测要素的最上和最下两条平行直线P1、P2之间形成定向最小包容区域,该区域间纵向距离即平行度误差f∥。为了方便直观观察,还可以将评定折线旋转至水平方向。
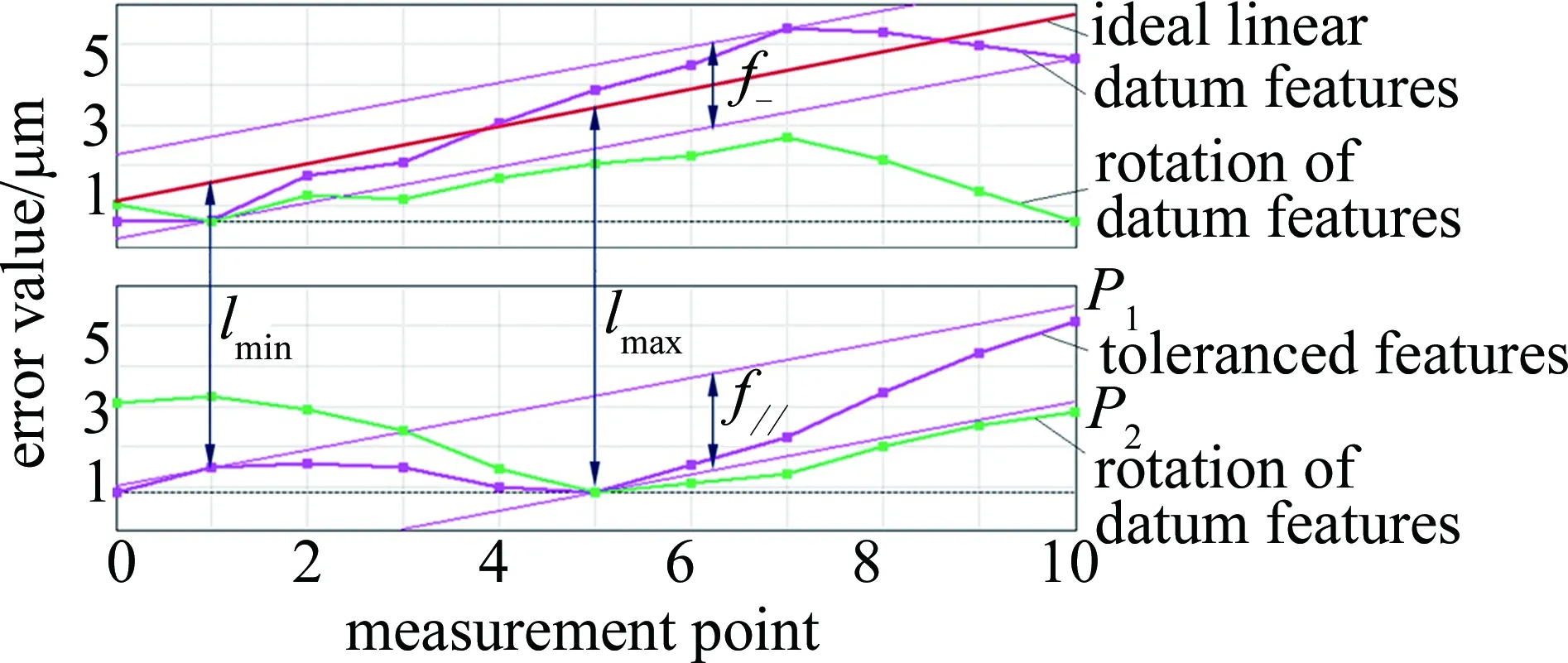
Fig.8 Schematic diagram of parallelism error evaluation(take parallel lines for example)
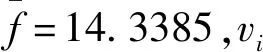

Table 1 Parallelism error evaluation results and analysis
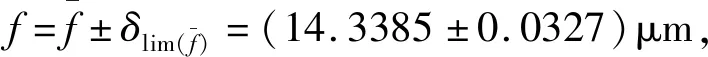
2.2 测量不确定度评定
对测量结果有影响的因素主要有:激光束的漂移、光束发散角、直角转向镜误差、光靶在被测表面的定位误差、外界杂散光及其它外界温湿度、振动噪声等干扰[17-20],其中激光发散角和直角转向镜误差,可以通过预先修正消除。另外,对PSD影响较大的因素还有背景光和暗电流,可通过调制滤波及加反向电流,两信号取差以抵消二者的影响。其它因素引起的不确定度分析如下。
(1)激光漂移等引起的不确定度urel(λ)。本系统中所选半导体激光器,波长650nm,光源稳定性小于0.05%[21],按矩形分布估计其不确定度为2.89×10-4。
(2)光靶定位引起的不确定度urel(p)。光靶在被测表面的定位误差可通过清洁表面及对中调整等精确控制,误差一般可控制在0.05%之内,按正态分布估计其不确定度为1.67×10-4。
(3)PSD引起的不确定度urel(d)。因PSD光敏面材料、电极等不均匀造成的非线性误差一般可控制在0.06%之内,按矩形分布估计其不确定度为3.46×10-4。
(4)电路及信号处理引起的不确定度urel(s)。经过采样降噪等处理,电路及信号处理产生的误差实验测量不高于0.05%,按三角分布估计其相对不确定度为2.04×10-4。
(5)环境因素引起的不确定度urel(e)。由于系统受到外界杂散光、大气抖动、温湿度、振动噪声等干扰,可通过严控室内测量环境有效抑制,综合实验验证表明该项误差总体控制不超过0.08%,按反正弦分布估计其不确定度为5.66×10-4。
因此,合成标准不确定度为:
7.701×10-4=0.077%<0.1%
(17)
由此可得系统的不确定度小于0.1%,测量准确度较高,满足系统设计要求。
3 结 论
利用激光准直法基于PSD对平行度误差测量技术进行了理论分析和测量系统设计,测量系统利用倒置望远镜结构二次透镜变换的方法,对准直激光束的发散角和光斑大小进行平衡,系统通过光学五棱镜转折光路,由PSD将测量位移经信号调理电路和数据采集及运算处理系统加以处理,从而实时显示测点相对基准线的位置,然后将数据传送到计算机,利用计算机专用软件以最小包容区域法快速评定出被测要素和基准要素两者之间的平行度位置误差,数据处理方便快捷,克服了传统平行度测量的低效稳定性重复性差等弱点,提升了系统适用性和先进性,通过激光准直和PSD传感技术的应用及信号处理,进一步提高了信噪比,测量精度高。经实验分析可知,此系统动态性好,测量结果可靠,具有较大的研究空间和应用价值。

