基于连续谱束缚态的高Q太赫兹全介质超表面

王鹏飞，贺风艳，刘建军，井绪峰，洪 治

(中国计量大学 太赫兹技术与应用研究所，杭州 310018)

引 言

近年来，由于可以实现高品质因子(quality factor,Q)谐振，连续谱束缚态(bound state in the continuum,BIC)受到了广泛的关注。BIC位于连续谱中，被系统完美地束缚且没有任何辐射[1-3]，其特点是Q无穷大或谐振的线宽为零。理论上，BIC是有无限寿命的暗模，在真实系统中无法观察，但通过有限尺寸、材料吸收损耗和其它外部扰动等，BIC会塌陷为有限Q因子的Fano谐振，即所谓的准BIC[4-5]。目前，BIC已在波导[6-7]、光栅[8-9]、光子晶体[10-11]及超材料[12-14]等结构中被广泛研究。

介质超材料中的BIC主要有两种类型：对称保护BIC[2]和弗里德希-温特根BIC(Friedrich-Wintgen BIC，F-W BIC)[15]。对称保护BIC出现在电磁波正入射(Γ=0，Γ是正方形晶格的第1个布里渊区高对称点)时，结构模式的空间对称性与外辐射波的空间对称性不匹配，造成束缚态与外辐射波之间无法耦合，即没有能量泄漏。可以通过斜入射或打破结构对称性，来构建与外界的辐射通道，这样理想BIC就转换为具有限线宽可观测光谱特征的准BIC[16-19]。而F-W BIC是通过两个模式发生相消干涉产生的，需要精确调整结构的参数[20]。若结构参数偏离理想BIC点，则变成有限Q值的准BIC[21]。此外，从多极子谐振的角度来看介质超材料中的BIC，通常有电偶(electric dipole,ED)、磁偶(magnetic dipole,MD)及环偶(toroidal dipole,TD)BIC。其中沿电磁波传播方向的纵向多极子BIC，如ED-BIC[22]、MD-BIC[23-25]及TD-BIC[17]可以归为对称保护BIC，因为纵向多极子本征模不能与正入射电磁波直接耦合,而横向多极子BIC则因易于与正入射电磁波耦合归为F-W BIC[17,21,26]。目前，BIC超材料已经应用于超低阈值激光器件[20,27]、非线性光学二次三次谐波产生[23,28]以及高灵敏度传感[29-32]等领域。

目前，利用高折射率硅圆柱体或其互补结构超材料已实现了高QTD谐振[33-36]及纵横向TD-BIC[17]，但对更具普遍意义的空心硅圆柱体结构的BIC超材料研究还较少，实际上已报道的圆柱体或圆盘结构只是对应空心圆柱体结构的特例。

本文中研究了一种由双硅空心圆柱体组成的太赫兹全介质BIC超表面。数值计算结果表明，该超表面在3.0THz左右支持一个纵向TD-BIC，即对称保护BIC。通过改变空心圆柱体的尺寸打破结构的C2v对称[17]，该超表面从理想的BIC转变成有限Q值的准BIC Fano谐振。此外，本文中还研究了该超表面几何结构参数对BIC频率的影响。

1 双空心硅圆柱体超表面结构设计

作者所研究的太赫兹波全介质超表面如图1a所示，是由沉积在环烯烃共聚物衬底上的呈周期性排列的空心高阻硅圆柱体组成。图1b是该超表面谐振单元结构的俯视图。谐振单元由两个不同尺寸空心圆柱体组成，其中谐振单元结构在x和y方向的周期Λx=Λy=Λ=62μm两个空心圆柱体具有相同的外环半径r1及不同的内环半径r2和r3，空心圆柱体中心之间的距离为Λx/2 (即空心圆柱体沿着x轴等间隔均匀分布)，空心圆柱体的高度h=24μm。用COMSOL Multiphysics软件进行了数值模拟，仿真计算中，考虑偏振沿x轴的太赫兹波正入射到该超表面上，在x和y方向上应用周期性边界条件，在z方向上采用了完美匹配层。硅的介电常数11.9，环烯烃共聚物的介电常数为2.34，采用环烯烃共聚物作为衬底是考虑到其介电常数低、吸收损耗小及器件制作方便[31]。该器件的制备方法如下：(1)将环烯烃共聚物涂覆到高阻硅表面作为衬底;(2)在高阻硅片旋涂光刻胶，并采用紫外光刻技术把掩模图案转移到光刻胶上;(3)用深反应离子刻蚀加工硅空心圆柱体[37]。此外，硅超材料结构器件也可以在石英衬底上进行制备[21]。

Fig.1 a—schematic diagram of a metasurface consisting of double hollow silicon cylinder b—top view of the unit cell

2 仿真计算结果及分析

2.1 Fano谐振

当两个空心圆柱体具有相同尺寸，即r2=r3时，该超表面具有C2v对称性，否则就是一个不对称结构，可以定义不对称度α=(|r2-r2|/r2)×100%。

首先，计算了不对称全介质超表面(r1=14μm,r2=7μm,r3=5μm)在2.6THz～3.2THz频率范围内的透射光谱，如图2a所示。从透射光谱中可以观察到，2.88THz频率处有一个很强的不对称Fano谐振，其品质因子Q值可以通过Fano拟合下式来计算[38-39]：

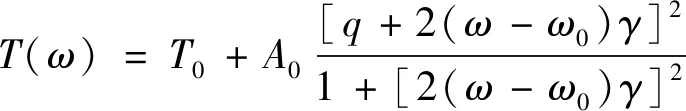
(1)

式中，q是决定谐振曲线不对称度的Fano拟合参数，ω0和γ分别代表谐振峰角频率和谐振线宽，T0是透过率基线偏移，A0是耦合系数，因此Q=ω0/γ。图2a中Fano拟合结果ω0和γ分别为2π ×2.88THz和2π×0.0084THz，所以Q=343。为了进一步定量分析这个Fano谐振的微观多极子属性，在笛卡尔坐标系下计算了该谐振的多极子散射功率[40]，包括ED，MD，TD，以及四电偶极子Qe和四磁偶极子Qm，如图2b所示。从图2b中可以明显地看出，在谐振中心处沿z轴方向的纵向TDz对谐振的贡献占主导地位，其次是沿y轴方向的MDy和Qm贡献大小基本相同，占据第2位，约为TDz散射功率的1/7，其它多极子的散射功率贡献量均小于TDz约1个数量级，说明这是一个TD谐振。同时，也给出了谐振中心在x-z平面处的电场强度E(见图2c)与x-y平面处的磁场强度H(见图2d)，进一步验证了其TD特性。从图2c中可以清晰地看出，在谐振单元结构内，电场主要集中于两个空心圆柱体之间，白色的箭头代表的是位移电流，左右的两个空心圆柱体内分别产生一个逆时针和顺时针的环形位移电流(黑色虚线箭头表示)，随之产生一个沿+y和-y方向磁场，故这样典型的成对环形位移电流会在x-y平面形成首尾相接的MD，如图2d中黑色虚线箭头所示，白色箭头代表的是MD，从而激发产生沿z轴方向的TDz。

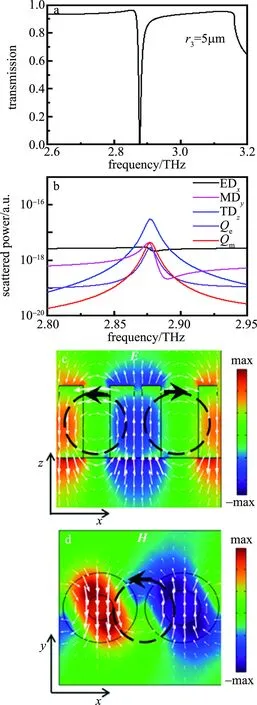
Fig.2 a—calculated transmission spectrum of the asymmetric metasurfaceb—scattered powers obtained by decomposition of the multipole in the Cartesian coordinate system c—electric field distributions d—magnetic field distributions

2.2 对称保护TD-BIC

接下来固定r1=14μm,r2=7μm,研究了TD谐振频率及Q随r3的变化曲线，如图3a所示。从图中可以明显地看出，当r3从1μm增加到13μm，谐振频率随着r3的增大而发生了380GHz蓝移，造成蓝移的原因是随着r3增大，空心圆柱体的有效折射率降低造成的[41-42]。另外，当r3从1μm增大到6μm，TD谐振的Q值从最初的55缓慢上升到1312,而当r3继续增加时,谐振的Q会急剧上升。特别是在对称结构超表面r3=7μm时，TD谐振在谐振频率2.94THz处线宽消失，谐振Q值无穷大。而当r3从7μm增加到13μm时，TD谐振Q值与r3在1μm～7μm变化时基本对称。这符合BIC的典型特征[21]。为此，作者计算了r2=r3=7μm时超表面在Χ′Γ和ΓΧ方向的色散曲线，图3b中给出了和上述TD谐振相关的一个横磁波(transvere magnetic,TM)模，记为mode 1。图3c、图3d中给出了在Γ=0.0点、mode 1在x-y平面的Ez及Hxy分布。可以看出它是一个TD谐振模。需要指出的是，在计算本征模时采用的是一个无基底的超表面结构，在Γ=0.0点，mode 1频率为3.13THz，加入基底后会导致TD本征模发生红移。按照C2v的对称性，mode 1是一个偶对称模式，而正入射电磁波则是奇对称的，两者之间是完全不耦合的[17,43]，所以该超表面在第一布里渊区，即Γ点形成的是具有无限Q值的对称保护BIC。此外，mode 1是一个纵向TD谐振模，不能与正入射电磁波直接耦合，也能说明这是一个对称保护BIC。

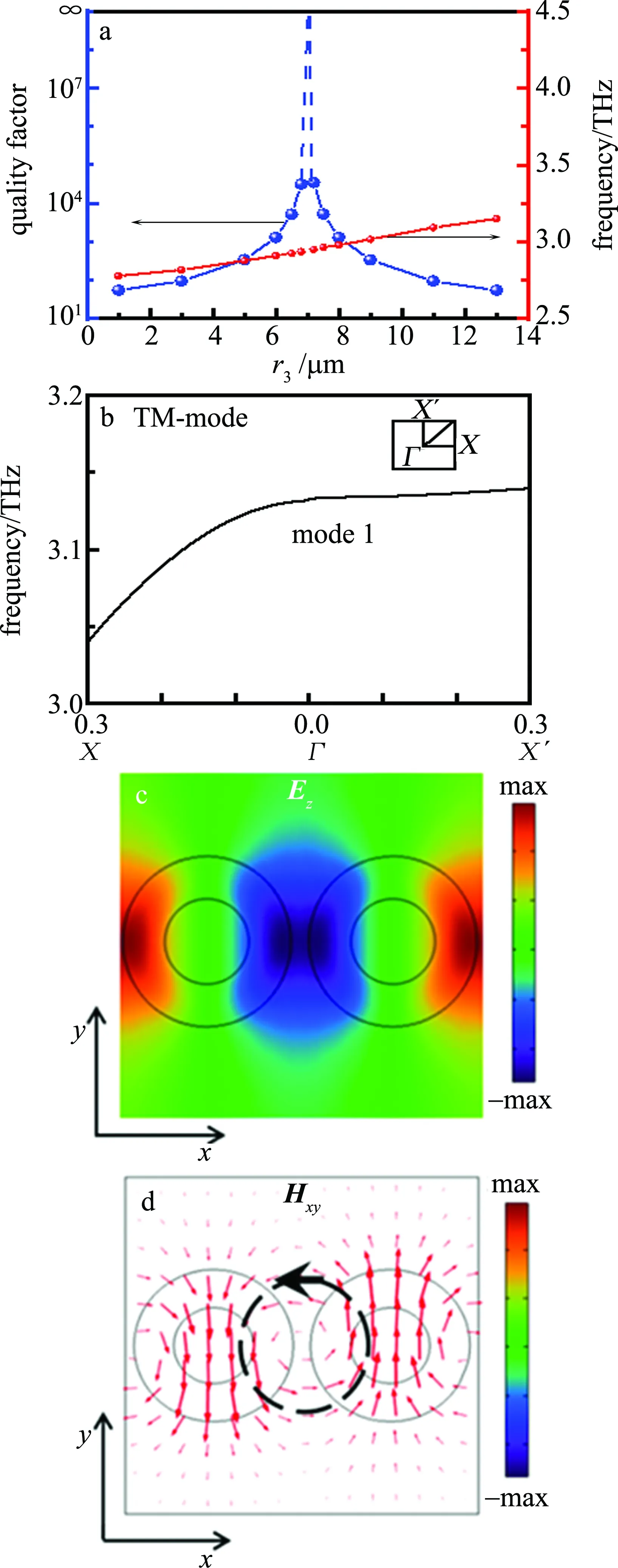
Fig.3 a—curves of Q factor and frequency of TD resonance with r3 b—dispersion curve of the related eigen mode in the Χ′Γ and ΓΧ directions when r2=r3=7μm, the upper right inset is the first Brillouin zone c—electric field distributions of mode 1 in the x-y plane d—magnetic field distributions of mode 1 in the x-y plane

对于图1a所示的对称结构超表面(r2=r3)，如果保持周期不变，只改变两个空心圆柱体之间的中心距离(即使空心圆柱体沿着x轴不等间隔分布)，则结构的C2v对称性没有被破坏，TD谐振应该仍保持理想TD-BIC特性。为了验证，当r2=r3=7μm，通过改变周期Λ=Λx=Λy(效果等同于改变空心圆柱体之间的中心距离)，计算了TD谐振的Q值跟周期Λ之间的关系，如图4a所示。可知随着周期Λ的变化，TD谐振的Q值的确始终保持在108以上。而对于参考文献[17,26,34,39]中的横向TD谐振，改变其谐振单元二聚体之间的间距或周期，其谐振Q值则会大大下降，表明这些谐振与对称保护BIC无关。

Fig.4 a—Q factor of the TD resonance with respect to the period Λ b—Q factor of the quasi-BIC with respect to the degree of asymmetry α

对于对称保护BIC，当结构的C2v对称性被破坏时(如r3≠7μm)，连续谱束缚态能量发生泄露，从理想BIC转变成有限Q值的准BIC，并且随着不对称度的增大，准BIC的Q值会越来越小，如图4b所示，准BIC的Q值和超表面结构不对称度α的负二次方成反比[44]。

2.3 结构参数对TD-BIC的影响

从以上分析可知，高QTD谐振的设计调控与TD理想BIC密切相关。为此，作者利用本征模分析方法研究了对称结构超表面几何参数对TD-BIC频率的影响。图5a是TD-BIC频率随空心圆柱体内环半径r2(=r3)的变化曲线，其它参数均与图1b保持一致。当r2从0μm增大到12μm过程中，TD-BIC频率从一开始的缓慢增加到后面的快速上升，从2.74THz变化到4.11THz。需要指出的是，当r2=0μm时，两个空心圆柱体结构超表面实际上变成了两个实心圆盘结构[17]。图5b中则是当r2=r3=7μm时TD-BIC频率随圆柱体高度h的变化曲线。从图中看出，当h从8μm增大到40μm时，TD-BIC频率从4.69THz快速减小到2.61THz；当h继续增大时，BIC频率则缓慢减小并趋于饱和。若要使TD-BIC频率往太赫兹低频段移动，则可以通过增大超表面结构周期Λ和空心圆柱体外环半径r1，如当Λ=100μm，r1=20μm时，TD-BIC频率为2.25THz；当继续增大结构尺寸到Λ=300μm,r1=60μm时，TD-BIC频率为0.72THz。

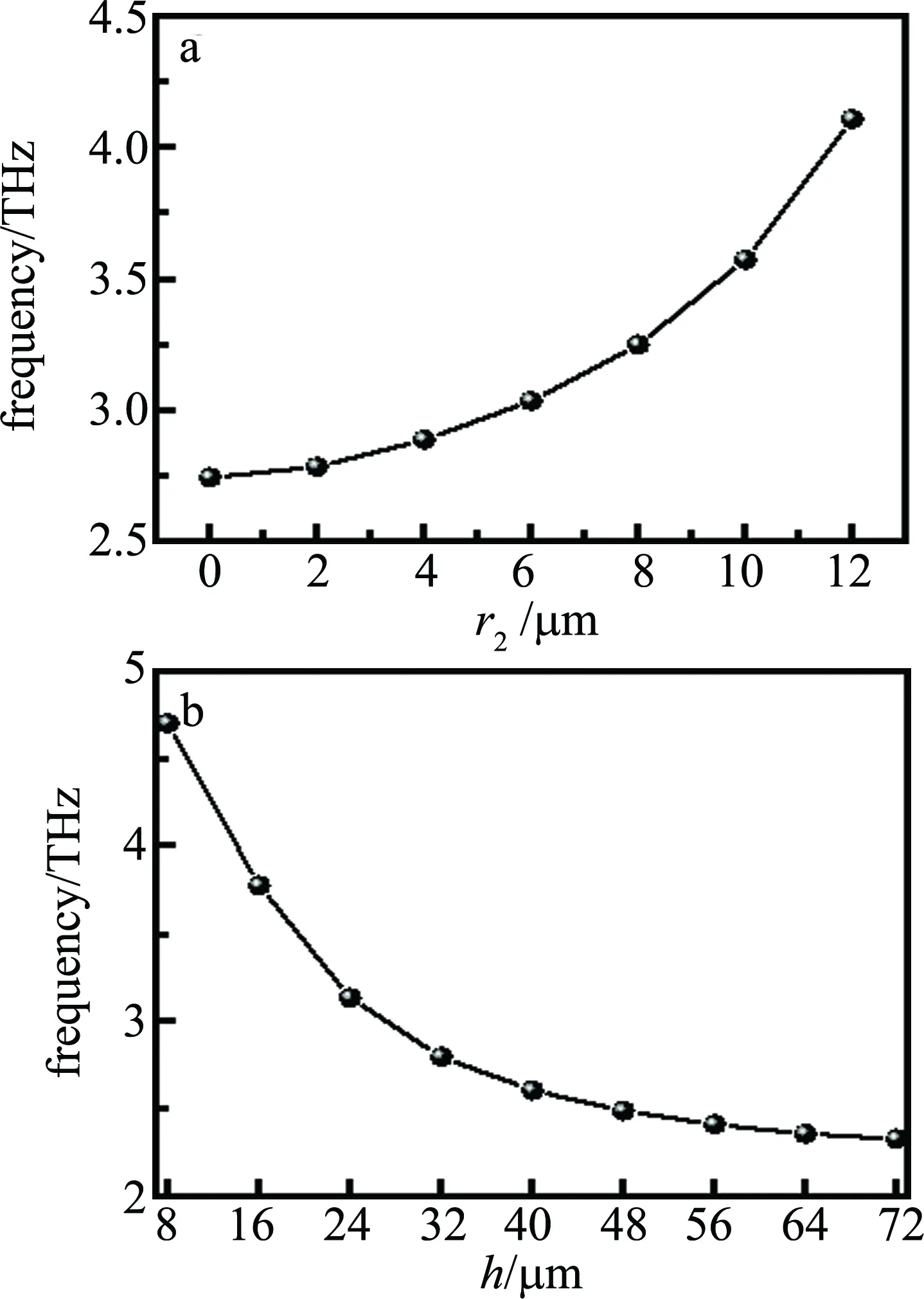
Fig.5 a—TD-BIC frequency with respect to the inner ring radius r2 b—TD-BIC frequency with respect to the height h

3 结 论

作者设计并数值研究了一种由双空心硅圆柱体组成的BIC全介质太赫兹超表面。通过计算多极子散射功率及近场电磁场分布分析，该超表面在3.0THz左右支持一个纵向TD-BIC。通过打破超表面的C2v结构对称性，获得了高Q准BIC谐振，且Q值可方便地通过空心圆柱体的内环半径，即改变结构的不对称度来调控。本征模计算结果表明，其和入射电磁波之间空间模式对称性不匹配，是一个对称保护BIC，而纵向TD谐振特性也表明，其不能与正入射电磁波直接耦合。此外，仅改变两空心圆柱体的中心距离或超表面结构周期而不破坏结构的C2v对称性情况下，计算获得的对称保护TD-BIC的Q值始终保持在108以上，进一步证实了其对称保护BIC特性。最后，利用本征模分析研究了结构几何参数对TD-BIC频率的影响，给出了该BIC超表面在太赫兹大频率范围工作的参数设计方法。双空心硅圆柱体全介质太赫兹超表面中的F-W BIC仍在研究中。