一种振荡浮子式波能发电装置的负载匹配模型的创建
何广华,汪 鹏,刘朝纲,栾政晓
(1.哈尔滨工业大学(威海) 海洋工程学院,山东 威海 264209;2.山东船舶技术研究院,山东 威海 264209)
振荡浮子式波浪能发电装置根据工作原理的不同可分为机械式[1]和液压式[2-3]。机械式是通过齿轮齿条等机械传动装置将浮子的运动转化为旋转运动,然后通过齿轮箱进行增速,最后在发电环节中通过发电机将旋转运动的机械能转化为电能。液压式则是利用液压系统进行发电。对于机械式的振荡浮子式波浪能发电装置,在其设计过程中,需要对某一确定的浮子进行负载匹配,即确定最佳的传动比和发电机的参数,以达到最佳发电功率。当使用水动力软件对浮子水动力性能进行计算时,只能在浮子上添加附加质量和负载阻尼等类型的负载,但是在实际情况中,发电机是一种较为复杂的负载,其阻尼系数难以根据产品基本参数信息查得,因此难以直接使用水动力软件计算以发电机为负载的浮子水动力响应,除此之外还需要考虑齿轮箱传动比的影响。因此本文提出了一种考虑上述影响因素的负载匹配模型,能够根据浮子快速确定最佳负载参数。
Ronald等[4-7]利用数学公式计算了漂浮圆柱体的水动力系数和无量纲波浪力振幅。张万超[8]等基于单浮体垂荡动力学模型得到了最优PTO阻尼,并分析了PTO对垂向运动RAO和俘获宽度比的影响,但是该动力学模型并没有考虑PTO的转动惯量的影响,并且PTO阻尼不能反映负载参数的影响。Felipe等[9-10]建立了双体系统的动力学模型,模型中包含了PTO的转动惯量并得到了PTO阻尼的表达式,但是该PTO阻尼是根据与发电机相连的电阻所得到的,没有充分考虑发电机自身性能参数的影响。李增亮等[11]研究了浮子式波能转换装置与发电机功率的最佳匹配,采用线性阻尼力代替直流发电机的特性,分析了波浪参数对匹配功率的影响规律以及变化负载对最大发电功率的影响。叶寅等[12-13]建立了波浪能装置液压转换系统的仿真模型,该系统包括了各液压元件与发电机,较好地模拟出了波浪输入下液压能量转换系统的发电特性曲线。张兰勇等[14]对直流力矩电机进行了理想建模,得到了直流电机的数学模型,同时也对电机的机械摩擦与内部损耗等非线性因素进行了分析。
本文利用Simulink搭建了机械式振荡浮子式波浪能发电装置的浮子垂荡运动模型,模型中考虑了传动比与发电机的影响。根据发电机的性能参数,对不同直径的浮子进行负载匹配。除此之外,本文从Simulink模型中推导出能够施加于水动力软件的附加质量和负载阻尼,并将水动力软件的计算结果与Simulink的计算结果进行了对比验证。所建模型可以应用于机械式振荡浮子式波浪能发电装置的设计、机械结构参数的确定和发电机的选型等,并对其他类型的波浪能发电装置的设计提供借鉴。
1 Simulink模型推导
1.1 浮子垂荡运动模型
采用机械传动的振荡浮子式波浪能发电装置的结构如图1所示,浮子与齿条固定在一起,齿条与齿轮啮合传动,齿轮转轴连接齿轮箱,齿轮箱连接发电机。发电机作为负载时,其具有阻尼,并且发电机转子的转动惯量J会导致转子转动时产生惯性转矩。将发电机的阻尼系数与转子的转动惯量折算到浮子上,分别得到负载阻尼CP和转子等效质量mJ,转子等效质量是添加在浮子上的附加质量,由此得到浮子动力学模型,如图2所示,其中kw为静水回复力刚度,μ33为垂荡附加质量,λ33为垂荡辐射阻尼,Fe为垂向波浪激励力。

图1 波浪能发电装置结构Fig.1 Structure diagram of wave energy converter

图2 浮子动力学模型Fig.2 Buoy dynamic model
本论文暂不考虑海流对机构垂向运动的影响,因此根据牛顿第二定律可以得到浮子在入射波作用下的动力学方程:
(1)
式中:m为浮子质量;z为浮子垂向运动位移;Fr为垂向辐射力;Fe为垂向波浪激励力;Fs为垂向静水回复力;FP为负载力。
根据势流理论,垂向辐射力Fr可分解为与浮子垂向运动加速度有关的附加质量力和与浮子垂向运动速度有关的辐射阻尼力。只考虑一阶作用力,垂向辐射力可表示为:
(2)
垂向波浪激励力Fe可用无量纲波浪力振幅表示:
(3)
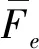
垂向静水回复力Fs可表示为:
Fs=-kwz=-ρgAwz
(4)
式中:kw为静水回复力刚度;Aw为水线面面积,对于圆柱型浮子Aw=πR2。
对于发电机系统,负载力FP可用负载阻尼CP和转子等效质量mJ表示:
(5)
将上述表达式整理可得浮子垂荡运动方程:
(6)
对式(6)两端进行拉式变换,可得浮子垂荡运动传递函数:
(7)
式中,M=m+μ33。
当无负载时,mJ=CP=0,此时浮子做自由垂荡运动,其传递函数为:
(8)
1.2 发电机负载方程
以直流电机作为发电环节中的发电机,电枢回路图如图3所示。转子转动从而在电枢回路中产生电枢电流和反电动势。

图3 电枢回路图Fig.3 Armature circuit diagram
根据电路理论,列出电枢回路的电压平衡方程:
(9)
电机感应电势方程为:
Ea=Ke·ωM
(10)
电磁转矩基本方程为:
TF=Kt·Ia
(11)
式中:Ea为反电动势;Ia为电枢电流;La为电枢电感;Ra为电枢电阻;Ke为反电动势系数,ωM为转子角速度;Kt为转矩系数,TF为电磁转矩。
将上述表达式进行拉式变换并整理可得电磁转矩传递函数:
(12)
由于机械摩擦、磁滞损耗以及涡流损耗等原因,在发电机中会产生阻转矩Tf,但是阻转矩Tf的影响较小,本论文中将此项忽略。由于转子的转动惯量J,转子转动时会产生惯性转矩TJ。因此负载转矩TP表示为:
TP=TF+TJ
(13)
1.3 传动机构方程与转子等效质量
对于采用机械传动的振荡浮子式波浪能发电装置,其传动机构为齿轮齿条和齿轮箱。齿轮轴与齿轮箱输入轴相连,齿轮箱输出轴与发电机转轴相连。此传动机构的方程为:
(14)

将转子的惯性转矩折算到浮子上,并与转子等效质量产生的惯性力相等,由此可得:
(15)
联立式(14)和式(15),可得转子等效质量为:
(16)
1.4 Simulink模型
结合1.1、1.2和1.3的内容,可以建立浮子垂荡运动的Simulink模型,如图4所示。该模型中的“lambda_33”为垂荡辐射阻尼λ33;“gamma”为等效传动系数γ。
该模型在浮子自由垂荡运动的基础上,加入发电机负载与等效传动系数。浮子运动的速度经过传动机构后,转换为发电机转子转动的角速度。发电机的负载转矩经过传动机构后,转换为负载力作用在浮子上。输入的垂向波浪激励力需要克服负载力才能驱动浮子进行运动。反电动势Ea与感应电流Ia的乘积为Simulink模型的理想瞬时发电功率。
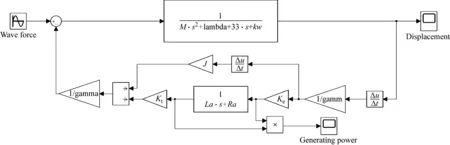
图4 仿真模型
1.5 系统传递函数的简化
为了验证图4中的Simulink模型计算结果,采用水动力软件计算相同负载下的浮子垂荡运动响应,因此需要根据Simulink模型来求解负载阻尼CP。
根据图4可得系统闭环传递函数为:
(17)
式中:X=Laγ2
Y=Raγ2
E=JLa+MLaγ2
F=JRa+(MRa+λ33La)γ2
G=KeKt+(kwLa+λ33Ra)γ2
H=kwRaγ2
由式(17)可知,Simulink模型为三阶系统,无法直接求出负载阻尼CP。式(7)为二阶系统,此二阶系统包含了负载阻尼CP。因此将三阶系统化简为二阶系统。
不妨令:
(18)
对式(18)分母中的多项式乘积进行展开,并令式(17)和式(18)分母中的各项系数对应相等,可得:
XMg=E
(19)
CgX+MgY=F
(20)
KgX+CgY=G
(21)
KgY=H
(22)
由式(19)和式(22)可得:
(23)
(24)
由式(20)可得:
(25)
由式(21)可得:
(26)
因为式(25)中只有垂荡辐射阻尼,式(26)中除了垂荡辐射阻尼,还包含有一项阻尼,所以选取式(26)为Cg的表达式,并定义:
(27)
综上,得到二阶系统表达式:
(28)
1.6 误差分析
式(17)与式(28)相减,可得三阶系统与二阶系统的误差传递函数E(s):
(29)
对式(3)进行拉式变换,得:
(30)
当输入为垂向波浪激励力Fe(s)时,输出为浮子垂向位移误差:
ΔZ(s)=E(s)·Fe(s)
(31)
对上式进行拉式逆变换,得到位移误差响应:
(32)
式中,σk为多项式Eσ3+Fσ2+Gσ+H的第k个根。
则相对位移误差为
(33)
式中,z3为三阶系统浮子垂荡位移响应。
2 结果与分析
2.1 浮子模型和仿真参数
本文中的计算模型为三种尺寸的圆柱型浮子,浮子参数如表1所示。在ANSYS AQWA中建立三种浮子的数值模型,网格最大单元尺寸分别为0.03 m、0.04 m、0.05 m,网格个数分别为15 388、23 036、27 754。2号浮子模型正视图和网格示意图如图5。

表1 圆柱型浮子参数Tab.1 Parameters of cylindrical buoys

图5 AQWA中2号浮子模型正视图(左)和网格示意图(右)Fig.5 Front view (left) and grid diagram (right) of buoy No.2 in AQWA
在AQWA中Hydrodynamic Diffraction模块计算圆柱型浮子垂荡运动的附加质量、辐射阻尼和无量纲波浪力振幅,计算频率为0.05~6.00 rad/s,频率个数为98,水深为50 m。求出三种浮子在表2所示“威海国家浅海综合试验场”海域平均海况下的水动力系数,如表3所示。

表2 海况Tab.2 Sea state
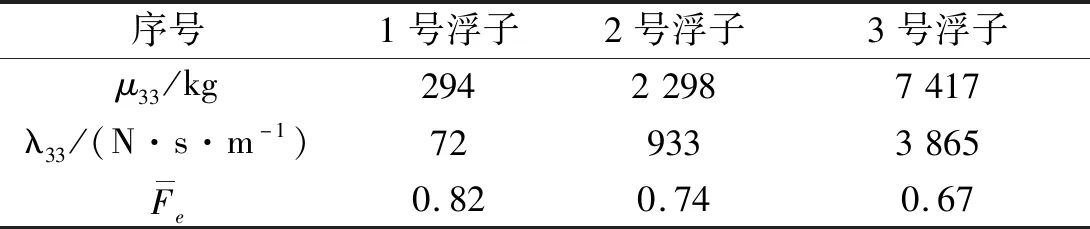
表3 浮子水动力系数Tab.3 Hydrodynamic coefficients of buoys
根据以上参数,计算得到浮子垂向波浪激励力,如表4所示。
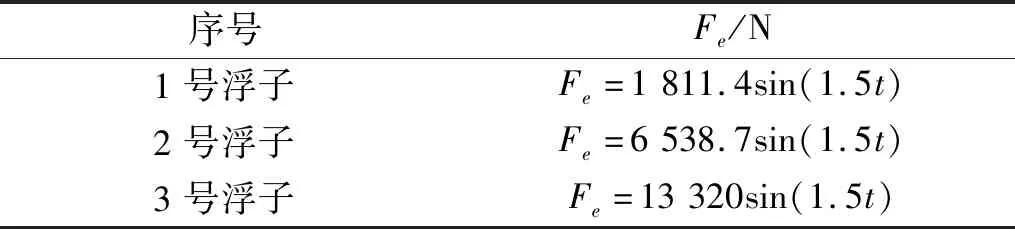
表4 浮子垂向波浪激励力Tab.4 Vertical wave excitation force of buoys
由式(16)和式(27)可知,传动机构中实际影响转子等效质量与负载阻尼的物理量是等效传动系数γ,为了便于研究与分析,取rg为0.1 m,通过改变传动比来改变等效传动系数。发电机的参数如表5所示。
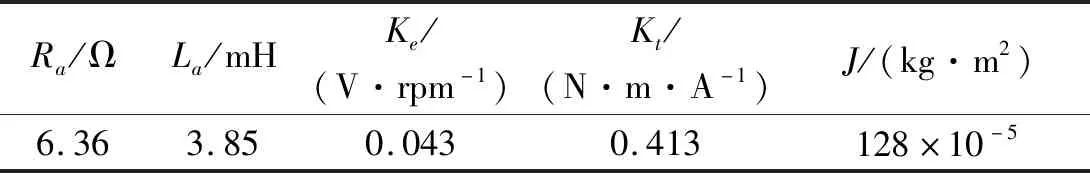
表5 130LY51型直流电机性能参数Tab.5 Performance parameters of 130LY51 DC motor
2.2 二阶系统输出响应误差
在本文的仿真参数下,计算得到不同直径浮子在不同传动比下的最大相对位移误差。由表6可知,简化后的二阶系统的最大相对位移误差均小于1%,误差很小,因此可以将二阶系统得出的负载阻尼与转子等效质量施加于AQWA中的垂荡浮子上,用AQWA的计算结果验证Simulink模型。

表6 二阶系统最大相对位移误差Tab.6 Maximum relative displacement error of second order system
2.3 负载参数
根据式(16)和式(27),计算得到不同传动比下的转子等效质量mJ与负载阻尼CP,如表7所示。在AQWA中Additional Added Mass和Additional Damping分别添加mJ和CP,只解放浮子的垂荡自由度,在表2的海况下进行时域计算,得到浮子的垂荡运动响应,并与Simulink模型浮子的运动响应做对比。
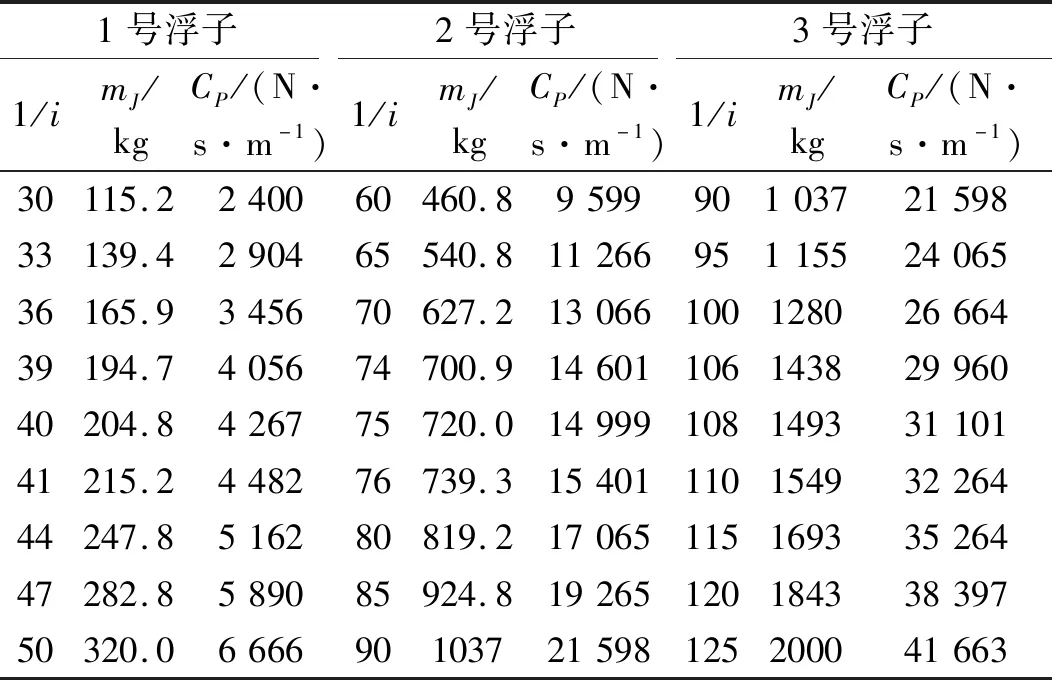
表7 转子等效质量与负载阻尼Tab.7 Equivalent mass of rotor and load damping
2.4 验证与分析
经Simulink模型计算得到三种浮子在不同传动比处的垂荡振幅AB,如表8所示。

表8 浮子在不同传动比处的垂荡振幅Tab.8 Heave amplitude of buoys at different transmission ratios
用式(34)对浮子垂荡运动的振幅进行无量纲化,用式(35)计算AQWA浮子瞬时发电功率,用式(36)计算Simulink浮子瞬时发电功率。用式(37)计算平均发电功率PB,平均发电功率为瞬时发电功率PI在一个波浪周期内的平均值。
(34)
式中,AB为浮子垂荡运动的振幅。
AQWA瞬时发电功率计算式为:
(35)
Simulink瞬时发电功率计算式为:
(36)
平均发电功率计算式为:
(37)
式中,T为入射波周期。
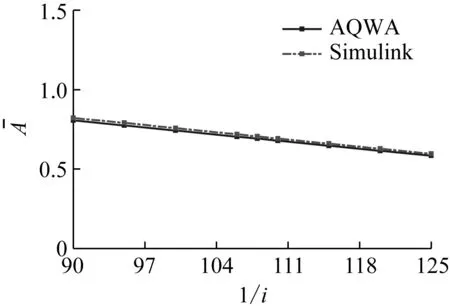
1号、2号和3号浮子在不同传动比处的无量纲垂荡振幅和平均发电功率如图6、7和8所示。从上述对比图中可以看出,Simulink模型的计算结果与AQWA的计算结果吻合很好,随着传动比倒数的增大,无量纲垂荡振幅近似呈现线性衰减,平均发电功率先增大后减小,出现了最大平均发电功率,并且同一浮子的两种计算结果在相同的传动比处达到最大平均发电功率,因此Simulink模型反映出了无量纲垂荡振幅和平均发电功率随传动比变化的趋势,并能准确预测出最佳发电功率点。
表9为Simulink模型与AQWA的计算误差。浮子垂荡振幅的计算误差不超过6 mm,对应的相对误差小于3%,平均发电功率幅值的相对误差小于4%。

(a) 浮子无量纲垂荡振幅
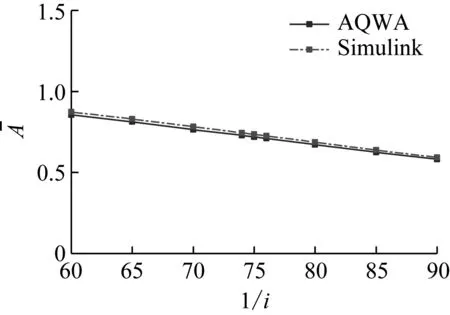
(a) 浮子无量纲垂荡振幅
(a) 浮子无量纲垂荡振幅
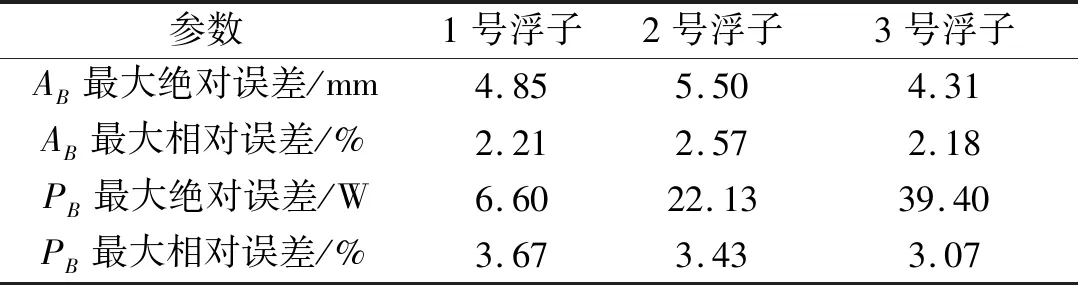
表9 计算误差Tab.9 Calculation errors
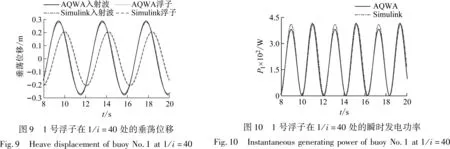
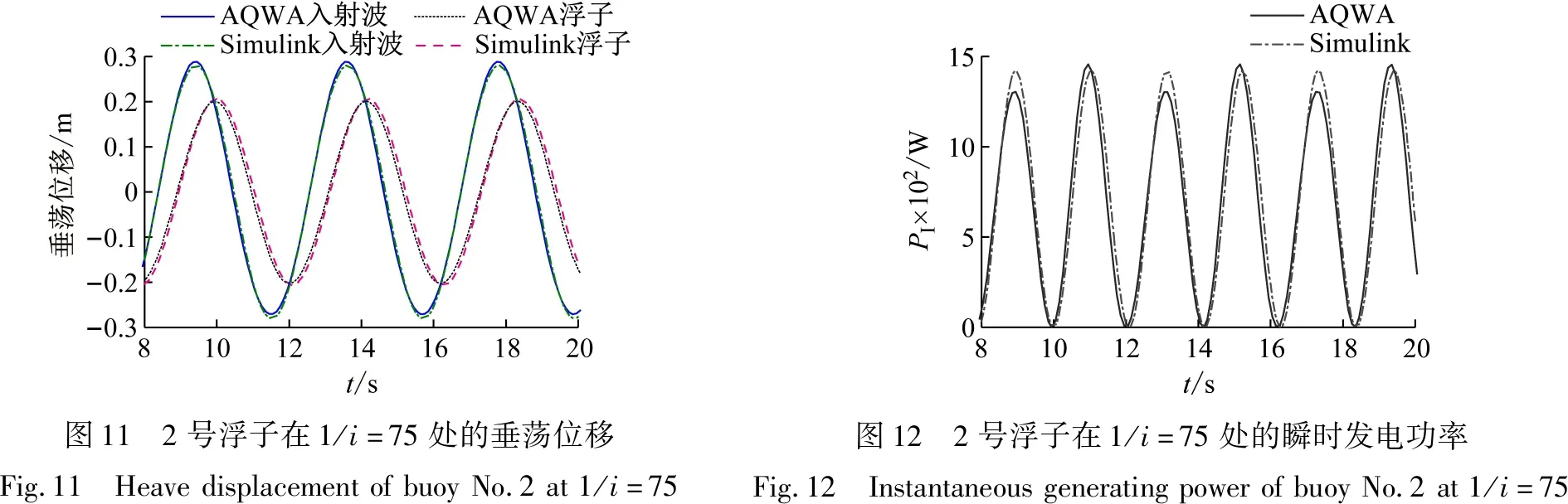
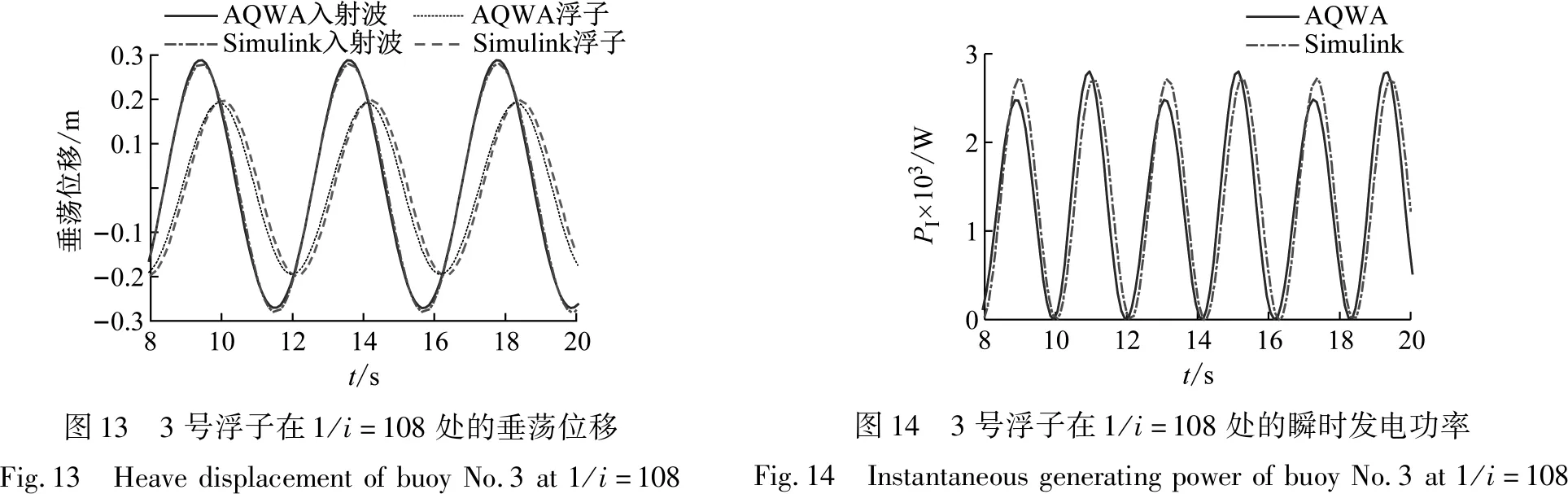
图9至图14为不同浮子在最佳传动比(最大发电功率处的传动比)处的垂荡位移和瞬时发电功率。从图中可以看出Simulink模型很好地反映出了浮子的垂荡运动。Simulink瞬时发电功率的计算结果是:在一个波浪周期内,出现两个峰值,并且两个峰值大小相等。但是AQWA瞬时发电功率的计算结果是:在一个波浪周期内出现的两个峰值大小不等,但是二者差值较小。这是因为在Simulink模型中,浮子垂荡运动的上行和下行最大垂荡速度相等;而在AQWA中浮子垂荡运动的上行和下行最大垂荡速度有微小差异,由于负载阻尼的数量级远大于浮子垂荡速度的数量级,因此这种微小差异在计算瞬时发电功率时被放大,产生了AQWA中一个波浪周期内出现的两个峰值大小不等的现象。
3 结 论
(1) Simulink与AQWA的计算结果吻合很好,充分反映了浮子垂荡运动振幅和平均发电功率幅值随负载变化的趋势,相对误差不超过4%。
(2) 本文中发电机的负载模型是根据发电机的基本性能参数和电磁理论推导计算得出,而不是单纯的阻尼参数,更贴合实际。
(3) Simulink与AQWA的计算结果均在相同的最佳负载阻尼下达到最大平均发电功率。在本文中,负载阻尼是根据传动比和发电机负载模型计算得到,能够用于确定最佳传动比。
(4) 最佳传动比与齿轮半径的乘积即为最佳等效传动系数,因此可以在保证最佳等效传动系数不变的前提下,根据设计需求灵活选择不同的齿轮半径rg,并得到对应的最佳传动比。
(5) 所建模型可以应用于振荡浮子式波浪能发电装置的设计、机械结构参数的确定和发电机的选型。

