基于NMPC的铝电解槽氧化铝浓度控制方法研究

阎 群,刘 波,路 辉,崔家瑞,黄若愚,王义轩,李 擎,曹 斌

(1.北京科技大学 自动化学院,北京 100083;2.贵阳铝镁设计研究院有限公司,贵州 贵阳 550003)

氧化铝浓度是铝电解生产过程中至关重要的参数[1]。铝电解生产时电解质中氧化铝浓度一般需要控制在1.5%～3%[2],过高容易在槽底生成氧化铝沉淀,降低铝电解的电流效率并且影响电解槽寿命;而过低则容易导致铝电解过程阳极效应频发,造成大量不必要的能源损耗和环境污染。所以,实现铝电解生产过程中氧化铝浓度精确控制对于铝电解槽的物料平衡、稳定高效运行具有十分重要的意义。

目前,国内外针对氧化铝浓度控制方法的研究已有许多,主要包括自适应控制[3]、槽电阻斜率控制[4]、模糊控制[5-6],以及多种方法的综合控制[7-8]等。文献[3]和文献[4]是利用槽电阻与氧化铝浓度的关系,通过不同下料速率的切换来实现氧化铝浓度的控制。这种控制思路能够有效估计氧化铝浓度,使电解槽处于基本稳定的工作状态,但存在控制动作相对粗犷、氧化铝浓度波动大等问题。文献[5]提出的模糊控制方法有效利用历史经验和专家知识,制定并不断修改模糊控制规则,实现较高的氧化铝浓度控制精度,但是存在模糊规则设置非常依赖专家知识和历史经验的问题。文献[7-8]结合多种控制方法的优点,进一步提高了氧化铝浓度控制的精度,但存在控制器结构复杂、计算所需时间长、控制成本高,难以在现有槽控机硬件系统上实现等问题。

为了建立能够完整描述铝电解过程非线性特性、便于与槽控机硬件系统结合,实现不依赖专家经验的氧化铝浓度的精确控制。本团队在氧化铝浓度预测[9]、氧化铝浓度软测量[10-11]、分布式阳极电流监测[12-13]、数字化铝电解槽系统框架设计[14]等方面做了大量研究工作。在前期工作基础上,本文提出了一种基于非线性模型预测控制的氧化铝浓度精确控制方法,其控制系统结构简图如图1所示。

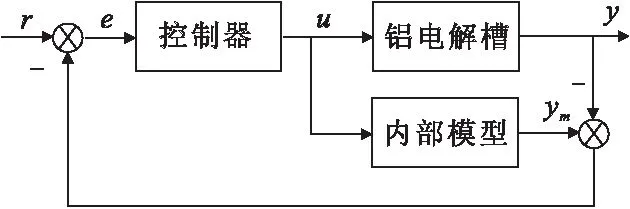
图1 模型预测控制系统结构简图

1 基于机理的内模输入输出变量选择

铝电解过程中表征铝电解槽运行状态的变量参数较多,如:下料量(下料间隔)、工作电压、分布式电流、电解温度、铝水平、电解质水平、分子比等。在铝电解稳定运行过程中,影响氧化铝浓度变化的主要有下料过程和极距调整过程。传统铝电解槽点式下料控制方式主要采用定时下料或者欠、过量切换下料[2],即固定下料量,通过改变下料间隔来实现下料控制。传统极距控制是基于槽电阻的区间控制[2],即根据工作电压与目标电压区间的比较来判断是否需要进行极距调整。

针对氧化铝浓度精确控制问题,通过综合考虑铝电解下料、极距调整等过程中下料量、工作电压、阳极分布式电流、电解温度、铝水平、电解质水平、分子比等关键性能指标变量的可控性、可测性,以及硬件装置的可实现性来选取建模变量。相关参数的特征、硬件在线检测可实现性等如表1所示。

表1 铝电解槽过程关键参数特征及选取情况

根据选取规则,最终选取了下料量和工作电压作为NMPC内模的输入变量,氧化铝浓度为输出变量。

2 基于Hammerstein结构的氧化铝浓度子空间建模

针对氧化铝浓度变化过程存在的非线性特性,采用Hammerstein模型结构作为铝电解过程氧化铝浓度控制系统的内模,如式(1)所示:

(1)

式中:t=1,…,N-1,u=[u1u2]T为内模的输入变量(下料量和工作电压);

yt——模型输出变量(氧化铝浓度);

xt——系统的状态;

f(ut)=〔f1(u1(t))f2(u2(t))〕T;

vt,wt——零均值高斯白噪声序列向量。

本文采用文献[15]提出的基于最小二乘支持向量机的非线性Hammerstein系统子空间辨识算法。该方法在子空间辨识(N4SID)算法的基础上进行了非线性扩展,使其能够实现对于Hammerstein模型结构的辨识。其辨识流程如图2所示。

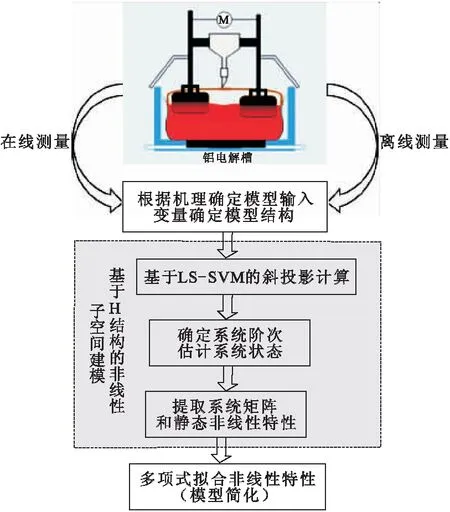
图2 建模流程

3 基于NMPC的氧化铝浓度控制系统设计

针对基于Hammerstein结构内模的特殊性,在求解控制律的时候通过逆运算移除控制系统的非线性项[16],需要考虑逆运算过程中的求根问题,设计图3所示的控制器结构。

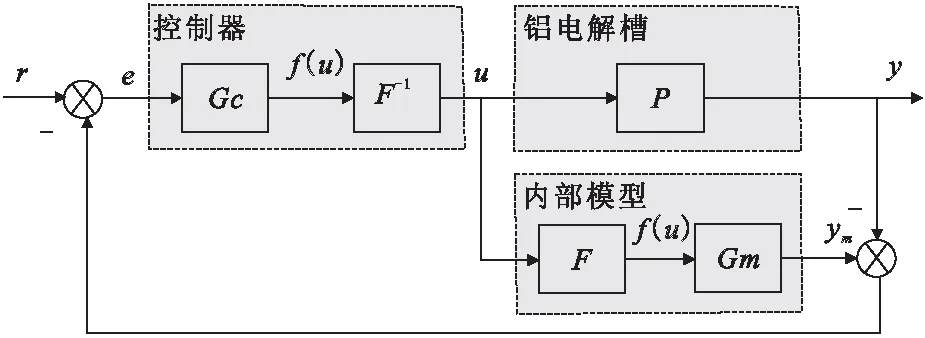
图3 非线性模型预测控制系统结构

图中,P为被控对象(铝电解槽),F和Gm串联构成Hammerstein结构的内模,Gc和F-1串联构成控制器,f(u)为中间变量。F为体现内模非线性特性的多项式函数,F-1为F的逆运算。

控制系统性能指标函数定义为:

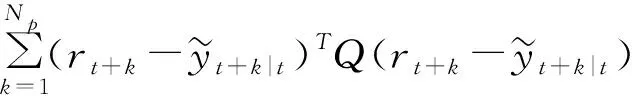
(2)

s.t.1)umin≤u≤umax

2)f(u)min≤f(u)≤f(u)max

s.t.umin≤u≤umax

3)rmin≤r≤rmax

式中:Np、Nc——分别为预测步长和控制步长;

△f(u)t+k-1——t+k-1时刻中间变量f(u)的增量(其中u=[u1u2]T);

rt+k和yt+k|t——分别为t+k时刻系统的设定输出值和预测输出值;

Q和R——分别为输出项和控制项的权重。

针对某400 kA铝电解槽,控制量u为下料量(u1)和工作电压(u2),r为氧化铝浓度设定值,需要满足物理条件约束(u1min≤u1≤u1max,u2min≤u2≤u2max,rmin≤r≤rmax)。由于非线性项为一元高次函数,存在无解和多解的情况,因此在性能指标中引入对f(u)的约束(f(u)min≤f(u)≤f(u)max),保证求逆过程获得具有实际物理意义的最优实根。

控制系统的控制策略为:在每一个采样时刻,将系统当前时刻的状态,控制系统设定值轨迹和内模代入性能指标函数中,根据两步法求解最佳控制律,将控制律的第一个分量作用于控制系统。在下一个采样时刻,重复该过程。具体求解步骤如下:

Step1:根据式(1)的状态空间方程进行递推,得到y(k+1|k)、y(k+2|k)…y(k+n|k)的递推表达式(3),其中y(k+n|k)表示k时刻预测k+n时刻系统的输出;

y(k+1|k)=Cx(k+1|k)+Df(u)(k+1|k)=CAx(k)+CBf(u)(k|k)+Df(u)(k+1|k)

y(k+2|k)=Cx(k+2|k)+Df(u)(k+2|k)=CA2x(k)+CABf(u)(k|k)+CBf(u)(k+1|k)+Df(u)(k+1|k)

y(k+n|k)=Cx(k+n-1|k)+Df(u)(k+n|k)=CAnx(k)+CAn-1Bf(u)(k|k)+

CAn-2Bf(u)(k+1|k)+…+CBf(u)(k+n-1|k)+Df(u)(k+n|k)

(3)

整理得:

Yk=Mx(k)+NUk

其中:

Yk=〔y(k+1|k)y(k+2|k)…y(k+n|k)〕T

M=〔CACA2CA3…CAn〕T

Uk=〔f(u)(k|k)f(u)(k+1|k)…f(u)(k+n|k)〕T

Step2:将递推式(3)代入式(2),可得性能指标函数的标准二次型:

(4)

式中:H=2(NTQN+R)

fT=2(Mx(k)-r)TQN

Step3:采用两步法求解最佳控制律。首先求解step2的二次型表达式(4),得到最优f(u);然后根据f(u)的反函数求解最佳控制律u。

4 仿真实验与结果分析

本文对某铝厂400 kA铝电解槽进行了数据采集,基于实际采集数据,建立了氧化铝浓度内模,并应用非线性模型预测控制实现对氧化铝浓度的控制,其中控制部分考虑了无干扰情况和存在下料量不准确、电压波动等干扰的情况。

4.1 数据采集

实验数据包括电解槽生产日报数据和现场采集数据。工作电压、下料量通过日报数据获取,下料间隔通过现场记录获取,氧化铝浓度数据通过现场采集电解质样品进行实验室化验获取。考虑到人工采集电解质样品的可操作性,将人工采样间隔设置为20 s,采样起始时刻设置为下料时刻、下料时刻+5 s、下料时刻+10 s、下料时刻+15 s。再通过插值实现下料周期内电解质样品数据的扩充。电解质现场采集过程如图4所示。

图4 电解质样品现场采集图

4.2 建模及模型误差分析

对现场采集的数据进行预处理后,令经验参数b=0.8,系统阶次k=2,多项式阶次m=2,建立的氧化铝浓度模型参数为:

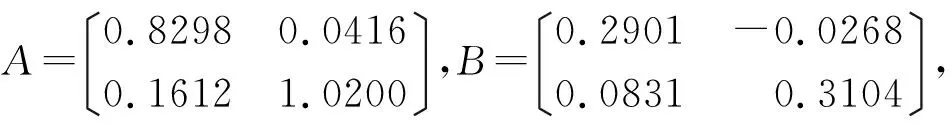
C=〔0.5421 -0.0337〕,D=〔0.2049 0.0426〕,

建立的内模的均方根误差(RMSE)为0.0930,且预测输出的变化趋势与实际值趋于一致,能够较完整描述氧化铝浓度的变化过程。

4.3 控制效果分析

某400 kA铝电解槽单次下料时间间隔为90 s左右,由于存在下料干扰等因素,考虑30 s的冗余,设置控制系统的预测时长为60 s,预测时域Np=12。同时,在综合考虑系统动态响应速度、稳态误差和计算复杂度的基础上,设置控制时域Nc=1、输出项权重Q=1和控制项权重R=0.05。

4.3.1 无干扰情况

氧化铝浓度初始值设定为1.5%,在100 s时刻和200 s时刻分别将氧化铝浓度设定值改为2%和2.5%,其控制量和输出响应分别如图5a～图5d所示。

由图5可以看出,实际的氧化铝浓度能够很快跟随设定值的变化,动态响应较快,而且稳态误差较小。

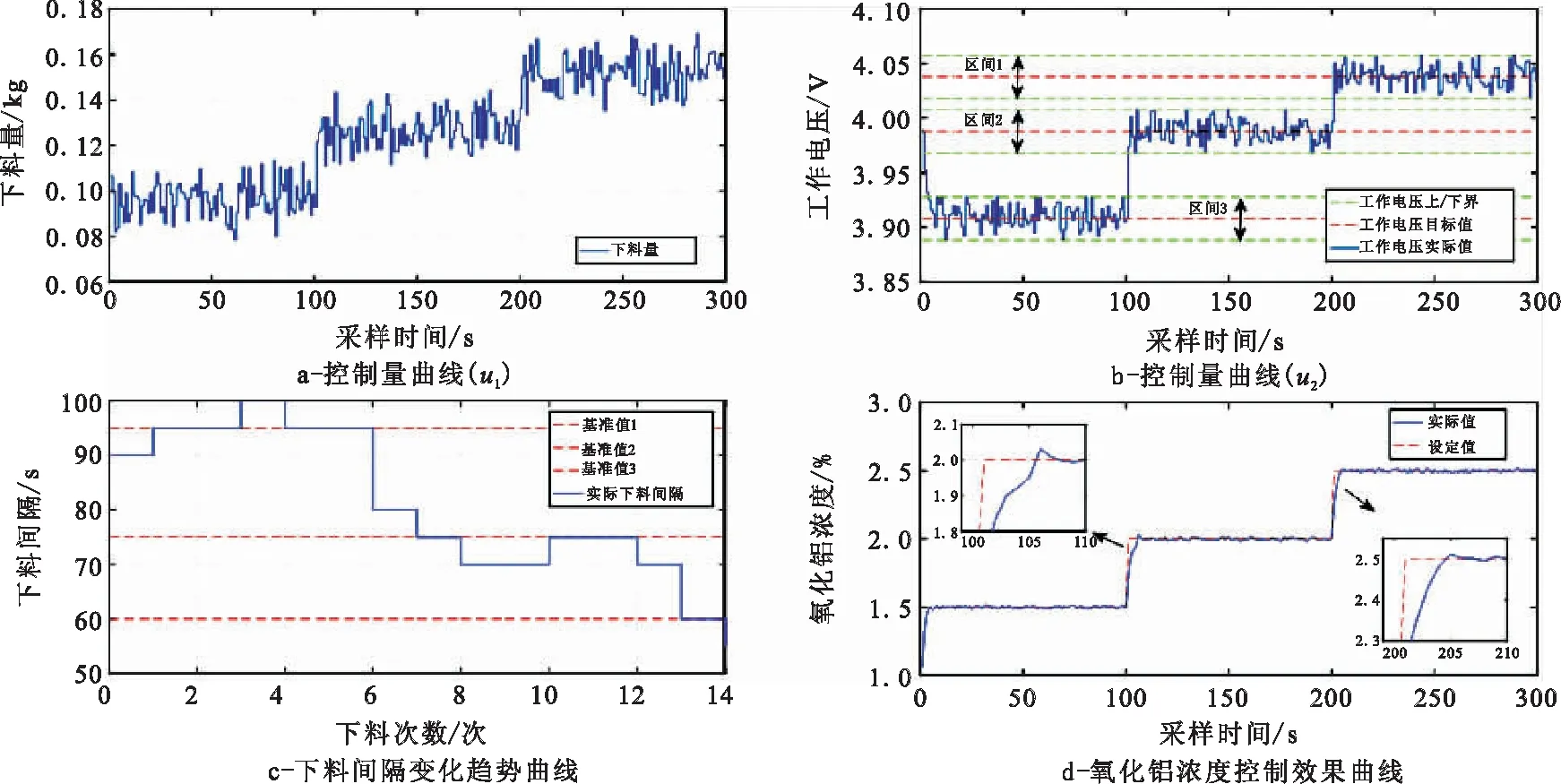
图5 无干扰情况下的模型预测控制效果

4.3.2 下料量不准确情况

考虑铝电解槽实际生产中单次下料的下料量并不一定非常准确,存在下料器堵塞以及人工与槽控机冲突导致短时内多次下料的情况。在100 s时刻将下料量分别增加和减少20%,模拟执行器故障和下料冲突的情况。以增加20%下料量为例,控制效果如图6所示。

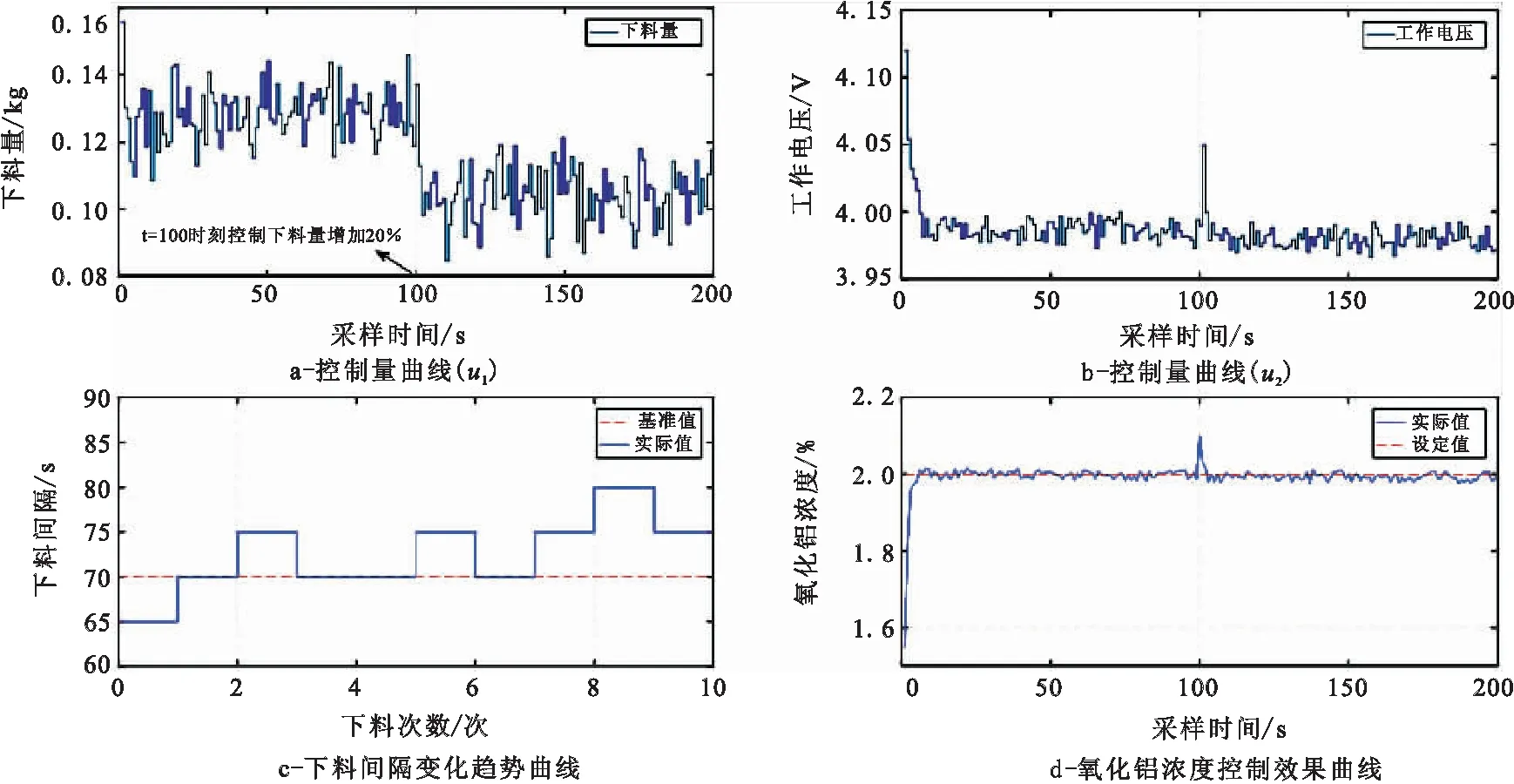
图6 t=100s时刻下料量增加20%的模型预测控制效果

从图6可以看出,在100 s时刻,控制系统会自动减小控制下料量,氧化铝浓度能够很快回到设定值,实现快速调整。此外,由图6a计算可得下料量减少的平均比例为19.5%,与引入的干扰基本一致,说明该控制系统能够有效抑制下料不准确的情况,有较强的鲁棒性。

4.3.3 电压波动情况

考虑到实际生产中,铝液、电解质波动等会引起工作电压波动,在采样时刻130～140 s和170～180 s分别引入工作电压波动,控制效果如图7所示。

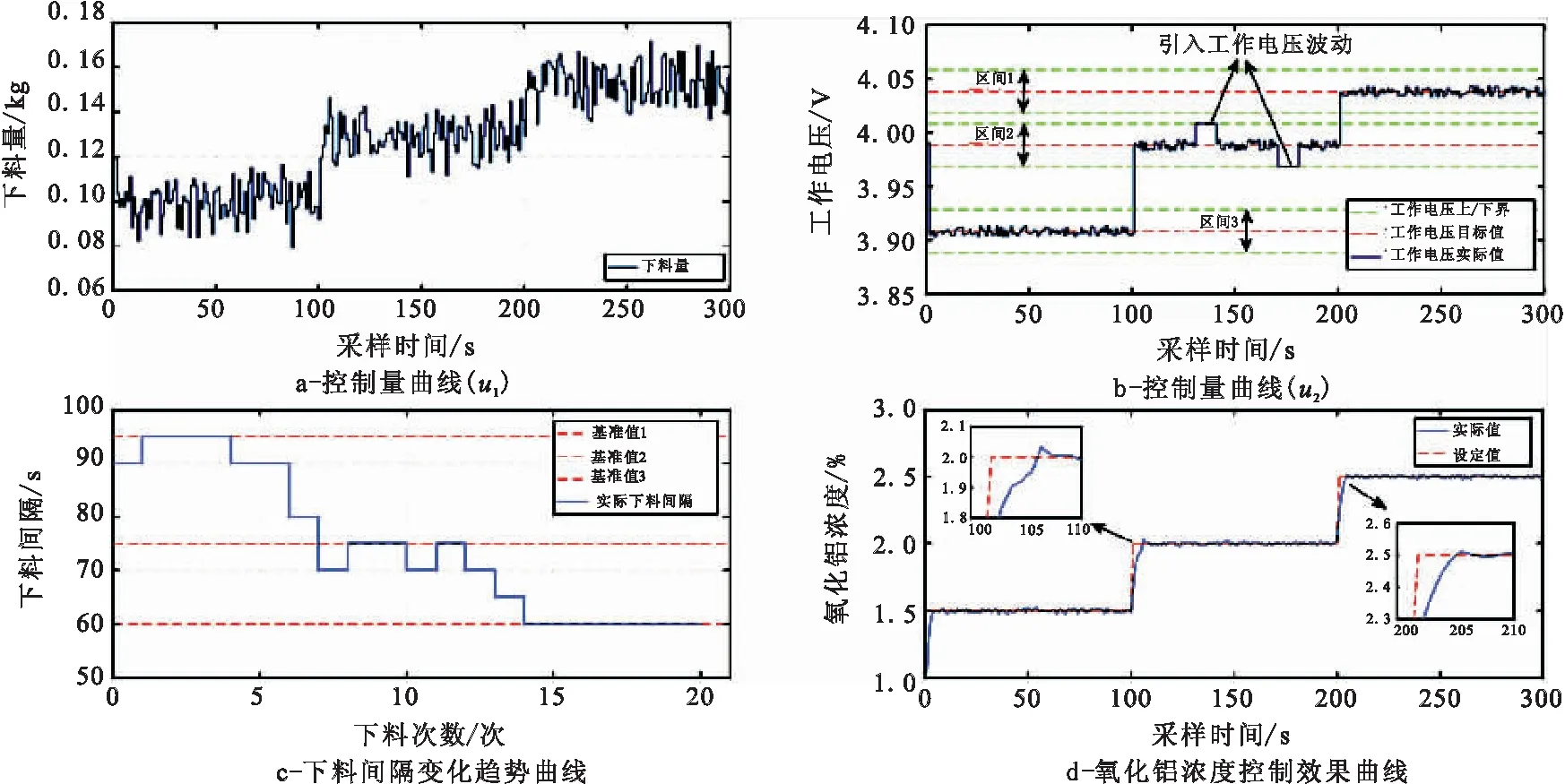
图7 考虑极距调整和电压波动的模型预测控制效果

由图7可知,相对于稳态时刻,在干扰引入时刻及持续时间内,氧化铝浓度波动较小,干扰消失后,系统能够快速恢复稳定,证明了该控制系统具有较强的抗干扰能力。

5 结 语

针对现有氧化铝浓度控制的不足,提出了一种基于非线性模型预测控制的氧化铝浓度控制方法。仿真实验表明:本文提出的控制方法能在不依赖于专家经验的基础上通过下料和极距调整实现氧化铝浓度的精确控制,为实际铝电解槽的氧化铝浓度控制提供一定的指导作用。目前只进行针对铝电解槽氧化铝浓度非线性模型预测控制的仿真研究,后续将进一步进行铝电解槽氧化铝浓度控制的实际工业实验。