Modeling of kinetic characteristics of alkaline-surfactant-polymerstrengthened foams decay under ultrasonic standing wave

Zhi-Hu Wng , Xio-Yu Liu , Hong-Qi Zhng , Yong Wng , Yun-Fei Xu ,Bo-Ling Peng , Yng Liu *

aKey Laboratory for Enhanced Oil & Gas Recovery of the Ministry of Education, Northeast Petroleum University, Daqing, Heilongjiang,163318, China

b Oil Recovery Plant No. 3, PetroChina Daqing Oilfield Company Limited, Daqing, Heilongjiang,163113, China

c Research Institute of Petroleum Exploration and Development, PetroChina, Beijing,100083, China

Keywords:Foaming performance Energy correlation model Decay kinetic Collapse mechanism ASP flooding Ultrasonic standing wave

ABSTRACT Foaming issues are encountered at the stages in crude oil production, transportation, processing, especially in chemical flooding enhanced oil recovery(EOR)oilfields.These accumulated foams would cause a lot of trouble for downstream operation.The destruction of foams under ultrasonic has been increasingly paying attention in the background of green oilfield development.This study focuses on the decay kinetic characteristics of alkaline-surfactant-polymer-strengthened foams under the ultrasonic standing wave.The performance of the diverse foams was characterized.A decay kinetic model incorporating the energy correlation was developed and validated. The factors that affect the decay kinetic characteristics were discussed. The results indicated that the collapse rate and the collapse volume fraction decreased when the foam size decreased, the gas-liquid ratio decreased and the surface tension increased. Ultrasonic standing wave parameters have a significant impact on the decay behavior of the foam. Both the ultrasonic frequency and ultrasonic amplitude were increased by 50%, the collapse volume fraction of foams increased by about 1.25 times in the identical irradiation time.The relative deviation between the measured results and the model prediction was less than 10%.The potential collapse mechanism was also explained using the principle of energy correlation of foam surface. This study is not only beneficial to provide a robust and rigorous way to defoam of produced liquid in the alkaline/surfactant/polymer(ASP)flooding EOR process but also meaningful to well understand the decay process of oil-based foams.

1. Introduction

Foams are colloidal systems comprising a gas being the dispersed phase and a liquid being the continuous phase,they can be classified into two broad groups:spherical foams and polyhedral foams.At a low gas content,the spherical foams occupy a dominant position. Transformation of spherical foams into polyhedral foams begins when the gas content in foam becomes higher than 50-75%(Weaire and Fu,1989; Platikanov and Exerowa, 2008). Foams are ubiquitous in industrial production,in some industrial cases,foams are desirable, but excessive foams can also hamper industrial processes (Okesanjo et al., 2020; Prins and Riet,1987; Gallego-Ju′arez et al., 2015). Oil-based foams may not be as familiar but have a similarly widespread, and important occurrence in the petroleum industry.Foams may be applied or encountered at all stages in the oil recovery and processing, such as oil well drilling, reservoir injection, oil well production, and oil treatment (Jiang et al., 2021;Samimi et al., 2020; Nowrouzi et al., 2020; Wang et al., 2021; Luo et al., 2022). Whereas, foaming, as well as scaling and emulsification, has a negative impact on oil-gas-water separation, metering,and transportation(Liu et al.,2018;Wang et al.,2019).In particular,alkali/surfactant/polymer (ASP) flooding process, due to the synergistic effect of alkali, surfactant, and polymer, is a promising oil displacement technology for the development of old oilfields in China (Jiang et al., 2019; Zhong et al., 2019; Wang et al., 2016).However,the breakthrough of ASP chemical agents in formation is responsible for the considerable content of alkali, surfactant, and polymer in produced liquid (Sheng, 2014; Zolfaghari et al., 2018;Huang and Zhang,2008;Zhong et al.,2022).Along with the release of dissolved gas in the crude oil and flow field disturbances in manifolds and pipelines,this is attributed to the fact that the foam formation conditions are more favorable,the foam characteristic is more complex,the foam type is more diverse,and the foam decay is more difficult in the production liquid (Shaban,1995; Liu and Rui,2022). It also causes difficulties in downstream equipment handling and process control. For such reasons, there is a great interest in the prevention,control,and destruction of foams in the promotion of the chemical enhanced oil recovery(EOR)technology.

Foam stability, as an important property of foam, has increasingly attracted attention in the application of foam.Foam films are an essential structural element to maintain foam stabilization and play a dominating role in the existence of foam.Together with the Plateau border boundaries and vertexes, the foam films form a unified capillary system(Govindu et al.,2019;Babamahmoudi and Riahi, 2018; Cox et al., 2001). The oil-water mixtures containing a certain amount of alkali, surfactant, and polymer flow in this system. These chemical agents form two adsorption layers on both film surfaces, which are responsible for the stability of the foam film and thus of the foam.A high surfactant content causes surface tension to decrease and hence the surface elasticity forces to be less negative (Yekeen et al., 2017). For this reason, Laskowski et al.(2003) and Małysa (1992) believed that the surface tension might not directly affect foam stability of polyhedral foams occurring in the petroleum industry,and that the surface elasticity forces might play a more important role. Elasticity, by definition, is the ratio of stress to strain, and represents a measure of propensity to restore the initial state following deformation (Malysa et al., 1981).Therefore,the elasticity of a foam film is sometimes considered as a“self-healing” capacity against external disturbance. The Gibbs elasticity of a film is defined as the ratio between the change in surface tension to the change in per unit area,the foam stability is stronger, the Gibbs elasticity of foam film is higher (Małysa,1992;Mysels et al.,1961; Christenson and Yaminsky,1995). For the ASP flooding produced liquid,it is difficult for the foam to collapse and decay due to the high concentration of surfactant,the surface Gibbs elasticity force is large, and the foam stability is strong, which brings great challenges to the efficient gathering and transportation of produced liquid in oilfield surface system.

There are various primary methods to prevent the foam formation or to break them after foam generated.Foaming control can be achieved by chemical or physical effects (Garrett, 2015). The most efficient conventional method for defoaming is a chemical method that is based on the use of antifoam agents, however,chemical antifoam agents can cause serious negative effects which can contaminate products and reduce mass transfer(Kougias et al.,2015; Ross and McBain, 1944). Physical methods try to rupture foams via thermal and electrical effects which nevertheless are generally expensive and energy-consuming (Dippenaar,1982; Zhu et al., 2022). The use of airborne ultrasonic energy for defoaming is based on irradiation of the foam with high-intensity ultrasonic waves. It represents a clean non-contact mechanical technique to break and suppress foam.Hence,ultrasonic waves offer a promising alternative to conventional chemical and physical defoaming techniques (Barigou, 2001). The theory of ultrasound defoaming was first proposed more than 70 years ago(Ross and McBain,1944),however, practical application of ultrasound had to begin more than 60 years ago when Gallego-Ju′arez and his group developed a piezoelectric power transducer working at 20 kHz (Gallego-Juarez et al., 1978). Sun and Lv (1995) believed that the introduction of the ultrasonic wave into liquid would remove foam in liquid, and the defoaming effect was affected by temperature,foam properties,and suspended particles. Previous studies have clearly shown that ultrasonic can both prevent foam formation and destroy foams stabilized with sodium dodecyl sulphonate surfactants and that vibrators with higher power consumption are more effective in breaking foams (Britan et al.,1992; Flores et al.,2019). In studying the effect of ultrasonic intensity at a frequency of 25.8 kHz on foaming soap solutions, a critical threshold acoustic intensity was found below which foam did not produce (Komarov et al., 2000;Rodriguez et al.,2010).Furthermore,it is also essential to consider that the foam structure controls its resistance to the effects of ultrasound. Polygonal foams with large diameters tend to collapse rapidly under low power ultrasound, while spherical foams with small diameters require higher strength.This is one of the reasons why different foams have different damage threshold strengths(Mawson et al., 2016). Wang and Blake (2011) studied the behaviour of non-spherical cavitation foams in the ultrasonic wave field.It was found that the foams remain approximately of a spherical shape when the acoustic pressure was small or was initiated at the node or antinode of the acoustic pressure field. When initiated between the node and antinode at higher acoustic pressures, the foam lost its spherical shape at the end of the collapse phase after only a few oscillations.Winterburn and Martin(2009)investigated the effect of low power ultrasound on detergent stabilized airwater foams. It was found that in the case of 40 kHz ultrasound,an increased liquid drainage rate was observed,and a pronounced increase and subsequent peak in a mean liquid hold-up, which occurred at 4 min, was observed. Zuo's group measured the foam structure rupture of CO2-flooding crude oil by a patented experimental ultrasonic de-foaming device, and proved that ultrasonic wave could accelerate the foam rupture (Zuo et al., 2017). Even though some uniform understanding about the defoaming of aqueous systems has been obtained in previous researches from theory to experiment under the action of ultrasonic, specific considerations are still needed for the produced liquid foams destruction in ultrasonic field originating from the emerging engineering problems of the oil industry.It is the fact that modeling to predict the decay of oil-based foams is a novel approach compared to previous studies in which foam bursting was verified experimentally(Zuo et al., 2017).

Even though the mechanisms of ultrasonic defoaming are known, the effect of each driving foam decay factor separately in the process, is not clear at all. This lack of knowledge shows the difficult nature of the subject. Hence, in the present study, the feasibility of ultrasonic waves as antifoam technology in destroying alkaline-surfactant-polymer-strengthened foams was investigated.The performance of the alkaline-surfactant-polymer-strengthened foams was characterized. The energy competition relationship of foam surface in the process of foam decay was established.A decay kinetic model considering the wave energy,the ultrasonic radiation energy,and the Gibbs free energy of foam surface in the ultrasonic standing wave field was developed. The effects of ultrasonic standing wave parameters and foam properties on the collapse rate and the collapse volume fraction were discussed,and validated by ultrasonic defoaming simulation experiments. Furthermore, the potential collapse mechanism was explained using the principle of energy correlation of foam surface.It can certainly provide support for the high-efficiency treatment technology of alkaline-surfactantpolymer-strengthened foam in the ASP flooding EOR process.

2. Experiments

2.1. Experimental materials

The crude oil was sampled from representative production well of theDaqing Oilfield(China).The physicalproperties of thecrude oil were determined according to the related standard test method(Wang et al.,2019;Xu et al.,2021).After considering the potential effects of water-dissolved ions on the foam structure, produced water from the same oilfield were employed as the aqueous phase.High purity methane gas was employed as dissolved gas to generate foam. The Na2CO3, petroleum sulfonate, and partially hydrolyzed polyacrylamide (HPAM), which are common oil displacement agents in the actual ASP flooding process,were employed to simulate the chemicals in the produced liquid.The detailed composition characteristics of the foaming liquid system are shown in Table 1.

2.2. Experimental setup and procedure

An experimental setup for simulating and evaluating the oilbased foam decay was improved from the one established in our previous work(Wang et al.,2021),as illustrated in Fig.1.The setup consisted of a liquid pumping system,gas injection system,speedcontrolled stirring system,controlled temperature bath,ultrasonic generator, foam height detection system, and data acquisition and control system. In the simulation experiment, the controlled temperature bath was firstly started to set temperature conditions for heating or maintaining the desired temperature. Then, the prepared liquid mixing crude oil, water, and chemicals with a certain composition characteristic was pumped into the foaming chamber.At the same time, the methane gas was injected into the foamingchamber at a certain pressure and flow. The speed-controlled stirring system was then employed to simulate the conditions of flow field disturbances. The pressure in the foaming chamber was adjusted by gas injection volume and pressure relief. When the foaming height in the foaming chamber tended to be constant,the speed-controlled stirring system was closed. The foaming height detection system and ultrasonic generator were opened at the same time. The ultrasonic generator was used with two vibrating probes, with the probe positioned at the top of the foaming chamber. The frequency of the ultrasonic generator operated at a wide range of 0-40 kHz,and the amplitude could be varied up to a maximum of 1×10-5m.The foaming height detection system was utilized to detect the foam height based on the principle that the generated foams are conductive.

Table 1 Composition characteristics of the foaming liquid system.

Fig.1. Schematic illustration of the experimental setup for ultrasonic standing wave defoaming.

As the core component of the experimental setup,the foam size and volume measurement system containing focused beam reflectance (FBRM) and particle video microscope (PVM)measuring units was immersed into the foaming chamber to test the size and number of foams in real-time, and the structural characteristics of foam would be obtained.Finally,the essential unit control, data acquisition, image display, and data processing were performed by the data acquisition and control system.

2.2.1. Surface tension test

The gas-liquid surface tension of the foaming system with different gas-liquid ratio was tested at 40°C by using the spinning drop method (Zhong et al., 2019; Xu et al.,2022).

2.2.2. Gas-liquid ratio test

In experiments,after injecting the prepared liquid and methane gas into the foaming chamber, the foams generated under the stirring condition and reached a maximum amount.This maximum amount is related to the properties and contents of crude oil,water,and chemicals. Then, the gas-liquid ratio of the foams can be determined by testing the increment of foams volume and decrement of liquid volume.

2.2.3. Foam height test

In experiments,the foaming and defoaming process progressed under a given gas-liquid ratio,temperature,stirring condition,and ultrasonic standing wave field.The foam height would be achieved by the means of the displacement of the vertical lifting motor in the foam height detection system.

2.2.4. Foam size and volume measurement

The size distribution and video microscope image of the foams would be real-time analyzed with FBRM and PVM,respectively.As mentioned above, when the FBRM probe was immersed into the foaming system in the foaming chamber, the emitted laser was reflected when it scans across the surface of the foam.The reflected signals were converted into electrical signals, and the number of foams was detected. The chord length could be obtained by the product of the reflectance time and laser scan speed. Simultaneously, three-dimensional structure imaging of the foams would be recorded by the PVM probe. The foam collapse rate in number can be calculated by collecting the variation of foam number with irradiation time in the ultrasonic standing wave field.

Furthermore,when the foam is assumed to be regular spherical,the chord length is the diameter of the foam. Assuming that these spherical foams are stacked in accordance with the Plateau rule,the foam volume during the foaming and defoaming process can be determined by the average foam diameter and foam number in the foaming chamber within the range of foaming height. And then,after reaching the maximum foaming height, the foam collapse volume fraction can be obtained when different ultrasonic standing wave field conditions are applied.

3. Mechanistic model

The decay and collapse of aqueous foams have been studied for a long time, and have formed very rich and perfect theoretical knowledge. They are however not suitable to be applied to oilbased foams analysis directly, and the collapse mechanism of oilbased foams, especially the alkaline-surfactant-polymerstrengthened oil-based foams, need to be further investigated.Foam drainage plays a pivotal role in determining its stability.Thus,various models,both theoretical and empirical,have been proposed in the literature to determine the foam drainage rate (Govindu et al., 2019; Ross and McBain, 1944; Bhakta and Ruckenstein,1997a; Fei et al., 2017). All the foam drainage models proposed so far are for the drainage in the absence of any foam breaking method i.e. for foam drainage under the natural conditions. Since under natural conditions, foam breakage starts only after a considerable time lag,all of the proposed models have concentrated on the liquid drainage rate and not on the foam collapse rate (Bhakta and Ruckenstein,1997a,1997b). As previous studies discussed, the effect of ultrasonic vibrations on the drainage rate was not as significant as it was on the foam collapse rate.Hence,here it has been attempted to correlate only the foam collapse rate in the presence of ultrasonic vibrations in terms of the various parameters studied.

According to previous studies (Rodriguez et al., 2010; Dedhia et al., 2004), it can be established that the forces caused by acoustic pressure and radiation pressure play a principal role in the destruction of foam. Such forces are counterbalanced by the internal forces of the foams due to the inside gas pressure and the surface tension and viscous forces of the liquid film. When the external perturbation is higher than the internal forces,the foam is deformed, the thickness of the liquid film edge is not uniform and the liquid flows through the capillary pressure to the thin part.The liquid film is supposed to rupture when the amplitude of the perturbation is enough to break the thickness (Pugh, 1996).Therefore, an important objective is to determine the energy competition between foam surfaces in the ultrasonic wave field.The generation of foam results in a large increase in surface area and requires an energy input into the system to overcome the counteracting force of surface tension of the bulk liquid phase.This is achieved by mechanical work in the form of induced turbulence or sparging of the gas phase into the bulk liquid.The input of energy gives the foam film a high Gibbs free energy,which keeps the foam stable(Bhakta and Ruckenstein,1997a;Dale et al.,1999).Therefore,the decay and collapse of foams require breaking this energy state.Rupture of foam films occurs when the surface waves generated by ultrasonic vibration acts on the foams,this process is thought to be achieved by ultrasonic energy breaking down the Gibbs free energy.

The decay behaviour of alkaline-surfactant-polymerstrengthened foam in the ultrasonic standing wave is shown in Fig. 2. The foam is located in the three-dimensional rectangular coordinate system with the spherical center as the origin.When the three-dimensional rectangular coordinate system is converted into a spherical coordinate system, the coordinates of any point on the foam film are(r,θ,φ).When an ultrasonic traveling wave generated by an ultrasonic source propagates in a limited space with boundary, another series of traveling wave with the same amplitude and frequency propagates along the same straight line due to the reflection characteristics, the two series of coherent waves propagating in the positive and negative directions along the x-axis synthesize an ultrasonic standing wave whose wave shape does not propagate along the traveling wave direction with time, its wave equation can be written as:

where y is the element displacement of the ultrasonic standing wave,m;A is the amplitude of ultrasonic traveling wave,m;λ is the wavelength of the ultrasonic traveling wave,m;x is the position of ultrasonic wave on x-axis, m; ω is the angular frequency of ultrasonic traveling wave,rad/s;t is the time of ultrasonic propagation,s.

The points with the largest and smallest amplitude are the antinode and node,respectively.The positions of both are fixed.The element vibrates between two adjacent nodes far away from half wavelength,and the distance between the antinode and the node is a quarter wavelength.

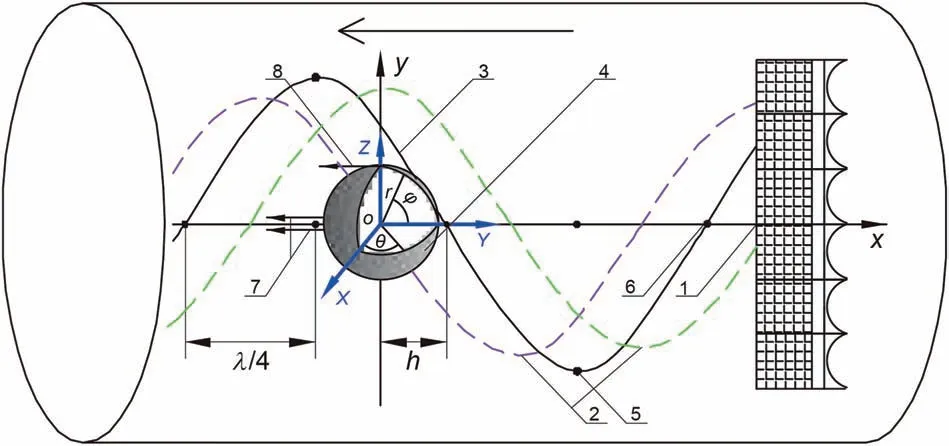
Fig. 2. Schematic diagram of the forced on the foam in the ultrasonic field.

The energy of ultrasonic waves through a certain section of the foam system per unit time is called the energy flow(Liu et al.,2014).When taking the section ds perpendicular to the direction of ultrasonic wave propagation in the foam system, the energy of ultrasonic waves through ds per unit time is equivalent to the energy of ultrasonic waves in the volume cds per unit time. Considering that the energy of ultrasonic wave through ds varies periodically, the energy flow of ultrasonic waves through the section ds per unit time is expressed as:

where Iu1is the foam system instantaneous energy flow density of the ultrasonic traveling wave propagating along the positive direction of the x-axis, W/m2; Iu2is the foam system instantaneous energy flow density of the ultrasonic traveling wave propagating along the negative direction of the x-axis, W/m2.

The instantaneous energy flow density of foam system in the ultrasonic standing wave formed by superposition is given by:

where I is the instantaneous energy flow density of foam system in the ultrasonic standing wave,W/m2.

The instantaneous energy flow density of the foam system is always 0 when the foam system is located at the position of antinode and node.At different moments,if the energy flow density of the ultrasonic standing wave field acting on the foam system is not 0,then the energy flow density of the foam system must originate from the ultrasonic standing wave between any wave antinode and its adjacent wave nodes.This is also consistent with the description of the local oscillation theory of ultrasonic standing wave energy and energy flow density by Li et al. (2015).

In the ultrasonic standing wave field, the average energy flow density of the foam system along the positive and negative directions of the x-axis is shown in Eqs. (8) and (9), respectively.

Considering the wave energy of foam system in ultrasonic standing wave field is the reflection of its energy flow density, the wave energy of foam subjected to ultrasonic standing wave field for a certain time can be written as:

where Ewais the wave energy of the single foam subjected to ultrasonic standing wave field for a certain time, J; r is single foam radius, m; δ is the gas-liquid ratio of the foam system; Δt is the irradiation time of ultrasonic standing waves.

Ultrasonic radiation force was first investigated in 1874 (Kundt and Lehmann,1874). Later, Boucher and Weiner (1963) attributed foam destruction by means of high-amplitude acoustic waves to ultrasonic radiation force.As shown in Fig.2,it can be assumed that the alkaline-surfactant-polymer-strengthened foam is a spherical body with radius r.The center of the sphere is the coordinate origin.In the three-dimensional rectangular coordinate system with the center of the sphere as the origin,as the propagation characteristics of the same wavefront surface in the ultrasonic field is the same,therefore, in a series of planes perpendicular to the Y-axis of the three-dimensional rectangular coordinate system, the ultrasonic radiation force of the foam is symmetrical on the upper and lower parts, and the two parts cancel each other out. The ultrasonic radiation force parallel to the Y-axis becomes its main force, so that the foam moves in the direction away from the ultrasonic source toward the position of the wave node, and the force in the ultrasonic wave field is uniform in all directions.When the whole force process is adiabatic, the ultrasonic radiation force on the foam surface can be described as(Yosioka and Kawasima,1995;Garrett,2015):

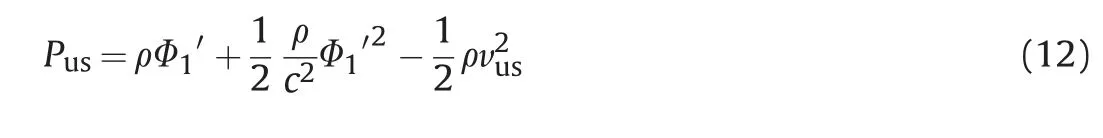
where Pusis the pressure generated by the ultrasonic radiation force on the spherical foam in the ultrasonic field, N/m2;Φ1is the first-order velocity potential of spherical foam vibration; vusis the vibration velocity of the spherical foam in the ultrasonic field,m/s.When the rectangular coordinate system is transformed into a spherical coordinate system,the surface area of the spherical foam is:

where S is foam surface area,m2;θ is the angle between radius and X-axis on the XOY in the three-dimensional rectangular coordinate system,rad;φ is the angle between radius and Y-axis on the YOZ in the three-dimensional rectangular coordinate system, rad.

Then the combined force of the ultrasonic radiation force on the foam surface at each location is expressed as:

where Fusis ultrasonic radiation force on foam surface in ultrasonic field, N.

Thus,

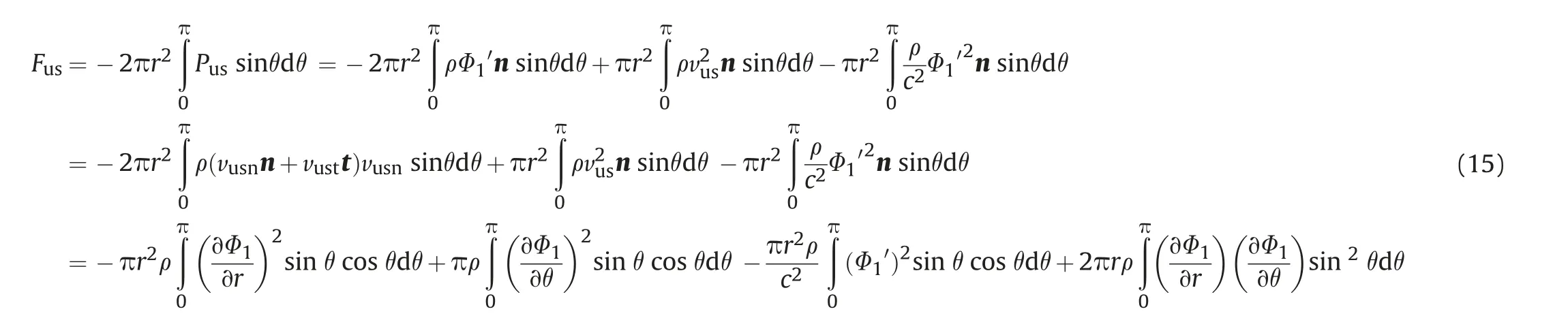
where vusnis the normal component of the velocity of a foam moving in an ultrasonic field; vustis tangential component of the velocity of a foam moving in an ultrasonic field; n is the normal vector of foam surface; t is tangential vector of foam surface.

The velocity potential of the ultrasonic traveling wave and the scattering velocity potential of spherical foam,which constitute the first-order velocity potential of foam vibration, are expanded step by step as spherical waves, respectively. Meanwhile, considering

The surface Gibbs free energy is the change in free energy that needs to be overcome when the foam ruptures.Since the forces on the molecules in the foam surface are different from those in the bulk,if the molecules are moved from the inside to the surface,the forces between the molecules within the foam must be overcome,and work must be done on the foam. When the temperature,pressure,and composition are constant,the work required to make the foam surface area dA change without considering the deformation of the foam is called surface work(Holzwarth and Malone,2001; Hou et al., 2018). It is expressed by:

where Esuis the Gibbs free energy of the single foam surface, J.

The Gibbs free energy on the alkaline-surfactant-polymerstrengthened foam surface is the energy change that needs to be overcome when these foams rupture,the decay and collapse of the foam is a competition between the energy possessed by the foam surface. Therefore, in the ultrasonic defoaming process, taking the energy balance of the foam in the ultrasonic standing wave field to maintain the steady state as the critical relationship, the wave energy, ultrasonic radiation energy, and Gibbs free energy of the foam surface in the ultrasonic standing wave field can be correlated as follows:

When the wave energy and the ultrasonic radiation energy acting on the foam system are stronger than the Gibbs free energy,the foam can be effectively decayed, and vice versa. For the alkaline-surfactant-polymer-strengthened oil-based foam system with a total number of N, the critical relationship between the maintenance of the steady state and the decay state of the foam that can collapse a number of ζN(0<ζ<1)within the irradiation time dt of the ultrasonic standing wave field can be expressed as:

where JNis the collapse rate in number of foams in the ultrasonic standing wave field,pcs/s.Consider that for the foam with a radius of r, the relationship between the total number N and the total volume V is:

where JVis the foam collapse rate in number volume in the ultrasonic standing wave field, m3/s; N is the total number of foams in ultrasonic standing wave field,pcs;V is the total volume of foams in ultrasonic standing wave field, m3.

Furthermore,taking the foaming process of alkaline-surfactantpolymer-strengthened foams in a cylindrical foaming chamber with a radius of R as an example,when the foam number is N,the foaming height is H, due to the total volume V of foam in this environment, the collapse volume fraction of foams can also be expressed as:where ψ is the collapse volume fraction of foams in the ultrasonic standing wave field, %; Vdis the volume of collapse foams in the ultrasonic standing wave field, m3.

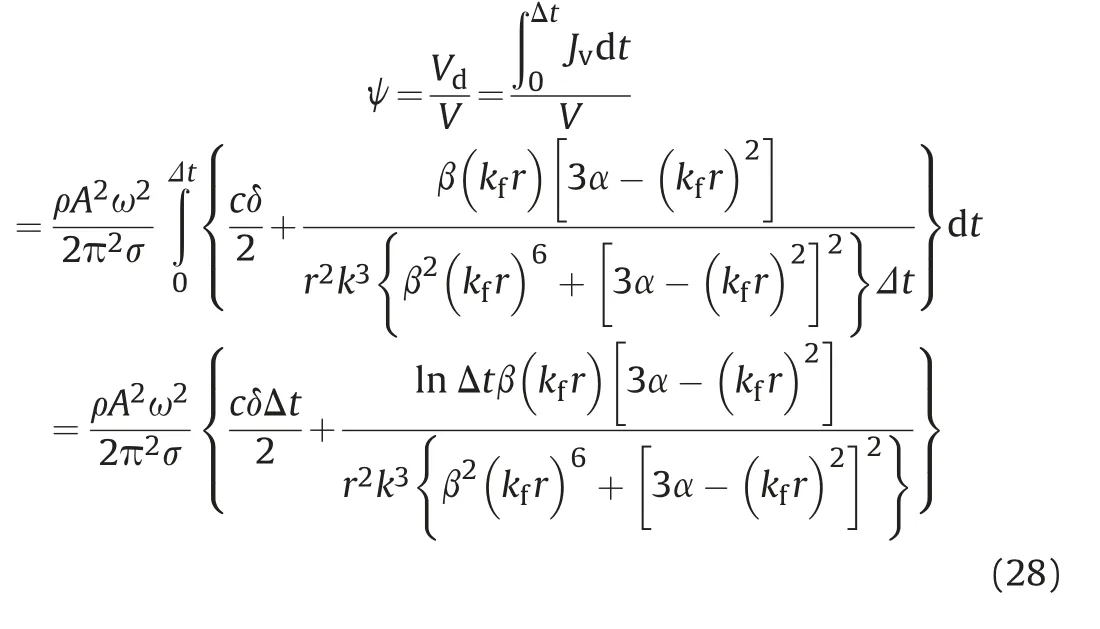
4. Results and discussion

4.1. Performance of alkaline-surfactant-polymer-strengthened foam

The experimental results indicated that when the foaming liquid system did not contain petroleum sulfonate surfactant and HPAM, the foaming behaviour was not obvious and the foam disappeared in a short time.With the increase of petroleum sulfonate surfactant and HPAM concentrations,the foaming height increased and the foam stability was significantly enhanced. However, it could be seen from Table 2 that foaming liquid system containing surfactant and HPAM with higher surface tension generated foams with smaller gas-liquid ratio, which revealed that the foam with higher surface tension had lower gas storage rate during its decay process. The strengthened foam stability can be attributed to the role of HPAM molecules in the system.This means that the foaming ability is dominated by the surfactant concentration and pH value that affect surface tension, while the stabilization ability is dominated by the viscoelastic HPAM.In the ASP flooding process,as the chemicals are produced with the liquid, the alkaline-surfactantpolymer-strengthened foam has both rapid foaming behaviour and good foam stabilization ability under the synergistic effect.

The size, number, and structure imaging of the foams generated from the foaming liquid system containing petroleum sulfonate surfactant and HPAM were shown in Fig. 3. It indicated that the lower surface tension was,the smaller mean chord length of foams was,the greater number of foams in any section of probe was,and the more concentrated of chord length distribution was(Fig.3a).Fig.3b intuitively showed that the stacking of foams presented more interlaced andconcentratedstateontheunitareaatlowsurfacetension.Withthe increase of HPAM concentration, the foam liquid film was obviously thickened,and the liquid film developed towards more regular Plateauborder boundary morphology. It was revealed that the foam stabilization ability of alkaline-surfactant-polymer-strengthened foam was also enhanced while the foaming behaviour was intensified.The foam film drainage would be hindered and bounded,the foam decay would be inhibited,and the foam life would be lengthened.

Table 2 Test results of surface tension and gas-liquid ratio of foams.

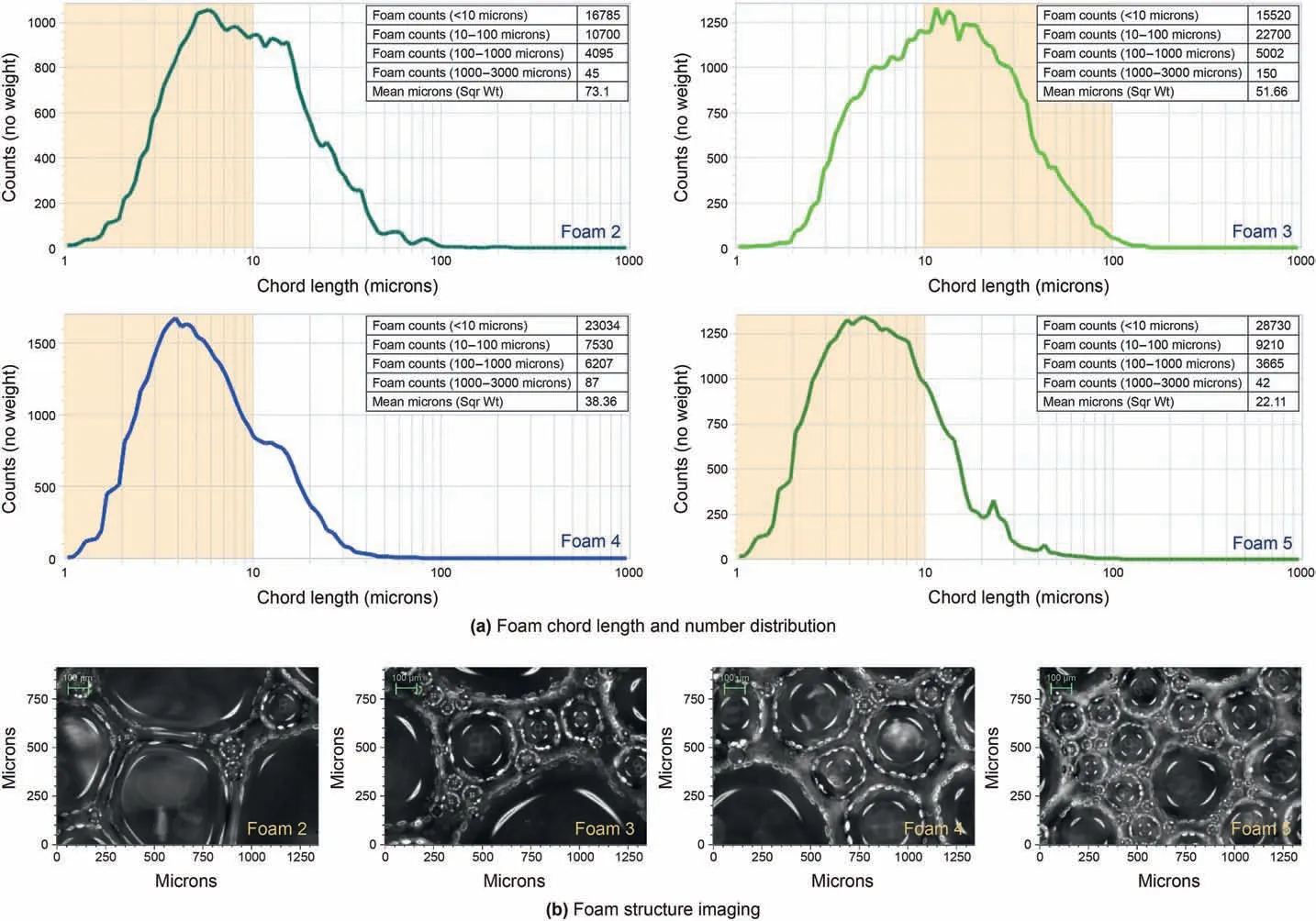
Fig. 3. Chord length, number, and structure imaging of the foams.

4.2. Effect of ultrasonic standing wave field parameters on decay kinetic characteristics

4.2.1. Irradiation time

The alkaline-surfactant-polymer-strengthened foams were radiated in the ultrasonic field with a frequency of 20 kHz and amplitude of 2×10-6m,4×10-6m,and 6×10-6m.The effect of irradiation time on the foam decay kinetic behaviour was predicted in Fig. 4. The maximum collapse rate in number of foams of 1.7×104pcs/s could be obtained when the foam was irradiated for 2×102T.In the same irradiation time,the collapse rate in number of foams with high amplitude was significantly higher than low amplitude.The collapse rate in number of foams decreased rapidly with the increase of irradiation time. However, the collapse rate decreased slightly and was unchanged with the further increase of irradiation time (Fig. 4a). According to Eq. (25), it was shown that there was a negative correlation between the irradiation time and the collapse rate in number of foams. The irradiation time had a certain effect on the collapse rate in number of foams in the short period of the initial stage of the ultrasonic standing wave,however,with the increase of the irradiation time, the collapse rate in number of foams would tend to be constant. Hence, the extended irradiation time was beneficial to the thorough foam decay.

In the ultrasonic standing wave field, the prolongation of the radiation time causes a continuous vibration of the foam surface,resulting in an increase of the wave energy on the foam surface.However,the Gibbs free energy of the foam surface is the inherent energy to maintain the foam stability,it has nothing to do with the change of radiation time, and the ultrasonic radiation energy changes only with the change of the ultrasonic standing wave parameter. Therefore, as the other ultrasonic standing wave parameters and foam properties are constant, the increase of irradiation time only increased the wave energy on the foam surface,and the ultrasonic radiation energy and the Gibbs free energy of foam surface remain unchanged.Hence,the energy balance relationship on the foam surface determined the optimal irradiation time required to realize the thorough decay of the foam for the same amplitude in a certain frequency of the standing wave field,excessive long irradiation time had little effect on improving the collapse rate in number of foams but rather increased unnecessary processing time.The collapse volume fraction of foams was linearly positive correlation with the irradiation time, it was close to 100%when the irradiation time is extended to a certain number of periods of the ultrasonic standing wave.The optimal irradiation time was 8.0 × 102T,1.4 × 103T, and 5.5 × 103T at the amplitude of 6.0 × 10-6m, 4.0 × 10-6m, and 2.0 × 10-6m, respectively, as shown in Fig. 4b. These prediction results were also validated by ultrasonic defoaming simulation experiments, and the relative deviation between the measured results and the model prediction was less than 10%. Slight acoustic cavitation occurred when the irradiation time exceeded the optimal irradiation time (Barigou,2001). Therefore, the ultrasonic irradiation time should be equal to the optimal irradiation time in practical operation.

4.2.2. Ultrasonic frequency and amplitude

The ultrasonic frequency and amplitude were found to be important parameters affecting the foam decay(Morey et al.,1999).The effect of ultrasonic frequency on the foam decay kinetic behaviour was predicted in Fig. 5. The collapse rate in number of foams increased in parabola shape with the increase of ultrasonic standing wave frequency.The trends of collapse rate were similar to different irradiation time, which was also observed by previous work (Xie et al., 2015). When a frequency was up to 40 kHz, the maximum collapse rate in number of foams reached 7.4×103pcs/s.At a high frequency, the effect of different irradiation time on the decay kinetic behaviour was close(Fig.5a).In order to analyze the mechanisms for this phenomenon,an explanation can be found in a previous study of the ultrasound effect on the defoaming of oilbased foam (Pal et al., 2020). In the same irradiation time, as the frequency of ultrasonic standing wave increased, the collapse volume fraction of foams increased until a thorough decay state which collapsed to 100% (Fig. 5a). Both wave energy and ultrasonic radiation energy acting on the foam surface increased,and their ability to resist Gibbs free energy on the foam surface increased with the increase of ultrasonic standing wave frequency until the critical equilibrium state that maintained the stability and decay of all the foams was broken.This indicates that frequency plays an essential role in the ultrasonic standing wave defoaming process.It is worth mentioning that it is different from defoaming process, the previous research had shown that the effect of ultrasonic frequency on breaking down oil and water emulsions was not obvious(Zuo et al.,2017). In the present study, the ultrasonic frequency presented an attractive effect on the foam collapse rate, which means that the characteristics of ultrasonic could greatly promote the destruction of foam. The ultrasonic defoaming simulation experiments were also well validated the model predictions.

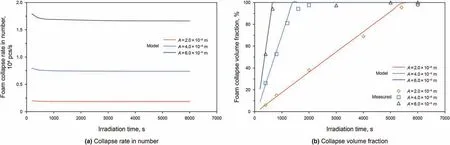
Fig. 4. Decay kinetic characteristics as a function of irradiation time.

According to the existing knowledge(Dedhia et al.,2004;Morey et al.,1999),the effect of ultrasonic amplitude on the foam collapse rate was similar to ultrasonic frequency. The foam collapse rate with ultrasonic amplitude was predicted in Fig.6.The collapse rate in number of foams also increased parabolically with the increase of ultrasonic standing wave amplitude, which agrees with the results mentioned above (Fig. 6a). It indicated that increasing the ultrasonic standing wave amplitude was beneficial to accelerate the foam decay as well as increasing the ultrasonic standing wave frequency.At the same time,the collapse volume fraction of foams can preferentially reach 100% at larger ultrasonic standing wave amplitude,and the thorough decay of foams was realized(Fig.6b).The mean relative deviation between the predicted and measured values was less than 10%. The energy input rate related to the ultrasound amplitude enhanced with the amplitude increased, this accelerated the foam collapse.It is known that the wave energy and ultrasonic radiation energy on the foam surface increase with the increase of the amplitude,while the Gibbs free energy on the foam surface remains unchanged.When the critical energy balance state that maintains the foam stability and decay is destroyed,the foam begins to collapse,and the corresponding amplitude is the optimal amplitude parameter. This is in good agreement with the results described in a report by Sandor and Stein(1993).

Furthermore, based on the analysis of Figs. 5 and 6, for the foaming system with the same physical properties, when the ultrasonic standing wave amplitude was 2 × 10-6m and the frequency increased from 20 kHz to 30 kHz, within the identical irradiation time,the collapse rate in number of foams and collapse volume fraction of foams increased from 1.86 × 103pcs/s and 36.20% to 4.15 × 103pcs/s and 82.70%, respectively. When the ultrasonic standing wave frequency was 20 kHz, the ultrasonic standing wave amplitude increased from 2.0 × 10-6m to 3.0×10-6m,within the identical irradiation time,the collapse rate in number of foams and collapse volume fraction of foams increased from 1.84×103pcs/s and 36.20%to 4.18×103pcs/s and 81.40%,respectively.It is obvious that the frequency and amplitude of the ultrasonic standing wave have a significant influence on the decay kinetic behaviour of oil-based foam,and the effect degree is equivalent.

4.3. Effect of foam performance on decay kinetic characteristics

4.3.1. Foam size

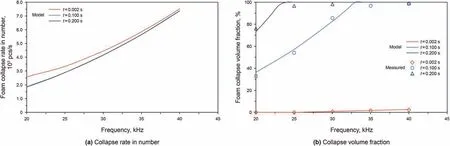
Fig. 5. Decay kinetic characteristics as a function of ultrasonic frequency.

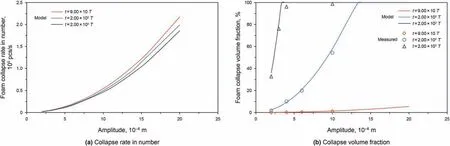
Fig. 6. Decay kinetic characteristics as a function of ultrasonic amplitude.

Fig. 7. Decay kinetic characteristics as a function of foam diameter.

The foam drainage and coalescence processes lead to liquid film weakening and foam average size increasing, producing a loss of self-support known as decay(Bhakta and Ruckenstein,1997a).The foam size plays a significant role in the decay behaviour of alkalinesurfactant-polymer-strengthened foams,and its effect on the foam decay kinetic behaviour was predicted in Fig. 7. The foam collapse rate in volume increased with the increase of foam diameter,which indicated that the collapse of large-size foam was faster than that of fine foam.Taking 2.0×102T of the irradiation time as an example,when the foam diameter was 860 μm, the foam collapse rate in volume corresponded to a minimum value of 7.0 × 10-7m3/s.When the foam diameter increased to 3000 μm,the foam collapse rate in volume was 2.6×10-5m3/s,which was the maximum value,and the changing trend of the collapse rate increased with the increase of the foam size in the identical irradiation time (Fig. 7a).This can be attributed that the wave energy and the surface Gibbs free energy of the foam surface increased with the increase of foam diameter, while the ultrasonic radiation energy decreased. This energy change characteristic resulted in the slow increase of the collapse volume fraction of foams with the increase of the average foam diameter under the identical irradiation time in the ultrasonic standing wave field, and tended to be stable gradually(Fig. 7b). In other words, even though the increase of foam size would accelerate its decay kinetic behaviour, for a certain amount of foam,when the foam size increased, the corresponding foam volume would increase by the third power of its diameter. This result was also well validated by the simulation experiments. As the original volume of foam system was large,the effect of foam size change on its collapse volume fraction was no longer obvious.However,with the increase of irradiation time, the collapse volume fraction of different foam sizes increased continuously, which still reflected the effect of irradiation time on the foam decay kinetic behaviour in the ultrasonic standing wave field.

4.3.2. Gas-liquid ratio

The gas-liquid ratio is regarded as a crucial driving factor for foam stabilization and decay, which has always been the focus of attention in the process of foam treatment(Wang et al.,2021).The effect of gas-liquid ratio on foam decay kinetic behaviour was predicted in Fig. 8. The collapse rate in number of foams under different irradiation times presented similar characteristics. It increased in a parabolic shape with the increase of the gas-liquid ratio of the foam system. This could already be an indication that foam decay was faster at a high gas-liquid ratio. In addition, there were different trends in the collapse rate in number of foams with the difference of irradiation time. When the irradiation time was 2 × 102T, the changing trend was steep, and the trend gradually became flat with the increase of irradiation time(Fig.8a).However,for the collapse volume fraction of foams, there was a slight difference, especially in the early irradiation period of ultrasonic standing wave (Fig. 8b). As the other ultrasonic standing wave parameters and foam properties are constant, the increase of the gas-liquid ratio of the foam system caused the increase of the wave energy and the decrease of the Gibbs free energy of foam surface,while the ultrasonic radiation energy only changed slightly,so that the total wave energy and the total ultrasonic radiation energy of the foam surface would completely resist to the total Gibbs free energy of foam surface. With the increase of radiation time, the collapse volume fraction of foams in the different gas-liquid ratios would increase towards thorough collapse state. Also, the measured foam collapse volume fraction distribution is consistent with the prediction results of the developed kinetic model.

4.3.3. Surface tension

Fig.9 showed the decay kinetic behaviour of foam with different surface tensions under the ultrasonic standing wave field.Although the foam with low surface tension was more stable, the collapse rate in number of foams decreased parabolically with the increase of surface tension in the ultrasonic standing wave field, which indicated that the collapse of the foam with lower surface tension was relatively faster(Fig.9a).This characteristic could be attributed to the decrease of the Gibbs free energy of the foam surface.As the surface tension decreased, the wave energy and the ultrasonic radiation energy of the foam surface remained constant, while the Gibbs free energy of foam surface that maintained foam stabilization decreased,and the energy relationship turned to a critical state that was beneficial to the decay and rupture of the foam,promoting the collapse of the foam.

When other ultrasonic standing wave parameters and foam properties are certain,the collapse rate in number and the collapse volume fraction of foams decreased with the decrease of surface tension at the identical irradiation time.However,both the collapse rate in number and the collapse volume fraction of foams at different surface tension increased as the irradiation time increased.When the irradiation time was 4.00×102T,the collapse rate in number and the collapse volume fraction of foams with the surface tension of 30 mN/m and 70 mN/m were 2.65 × 103pcs/s,1.00 × 103pcs/s and 7.93 %, 2.71%, respectively. When the irradiation time was 2.00 × 103T, they increased to 2.65 × 103pcs/s,9.43 × 102pcs/s and 50.50%,17.91%, respectively. Moreover, it can be seen from Figs.7 and 9 that the effect of surface tension on foam decay kinetic behaviour is more significant than the effect of foam size in the ultrasonic standing wave field with certain parameters.

5. Conclusions

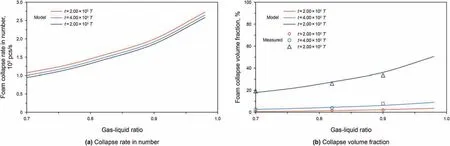
Fig. 8. Decay kinetic characteristics as a function of gas-liquid ratio.

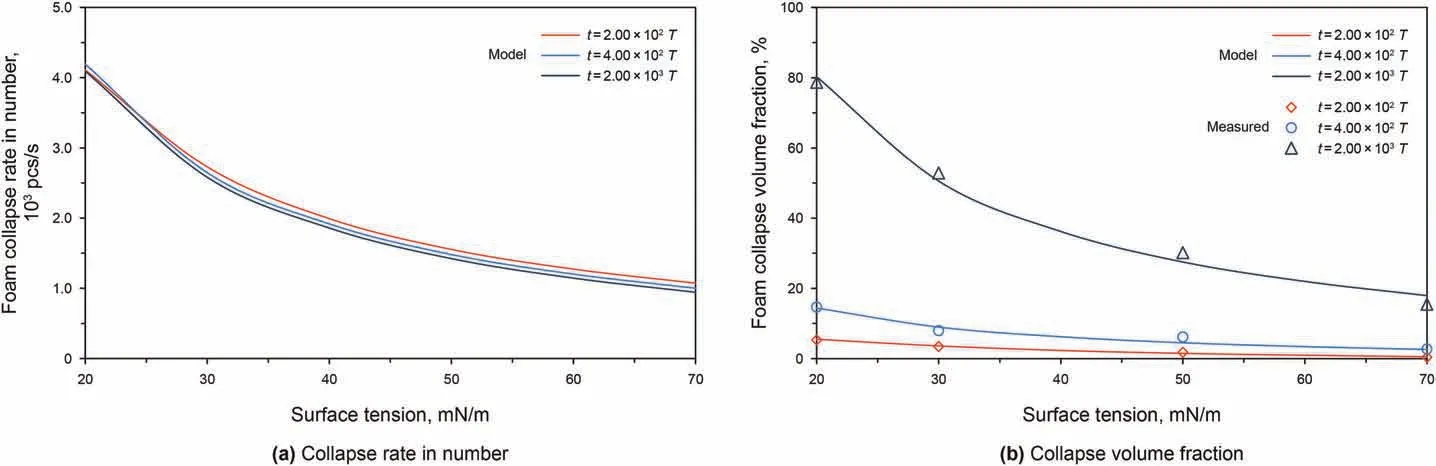
Fig. 9. Decay kinetic characteristics as a function of surface tension.

The alkaline-surfactant-polymer-strengthened foam is commonly encountered in produced liquid of oilfield applying ASP flooding EOR process. The performance of the diverse foams was characterized. A kinetic model was developed to investigate the decay behaviour and collapse characteristic of the foams under ultrasonic standing wave field. The effects of ultrasonic standing wave parameters and foam properties on the collapse rate and the collapse volume fraction were discussed. The decay kinetic model was well validated by ultrasonic defoaming simulation experiments. The potential collapse mechanism was explained using the principle of energy correlation of foam surface. The major conclusions are as follows:

(1) The recent progress demonstrates that diverse foams will be generated in produced liquid of the ASP flooding EOR process. Efficient gathering, metering, transportation, and in particular, separation in oilfield surface engineering are restricted. The foaming ability of alkaline-surfactantpolymer-strengthened foam is mainly driven by surfactant concentration and pH value that affect surface tension, the stabilization ability is mainly driven by the viscoelastic HPAM.

(2) The ultrasonic standing wave destroying alkaline-surfactantpolymer-strengthened foam is a potential method due to a reasonable critical relationship of wave energy, ultrasonic radiation energy,and Gibbs free energy of foam surface.The decay kinetic model incorporating the energy correlation could predict the collapse characteristics of foams with different properties and optimize the ultrasonic standing wave parameters. The prediction results showed that the collapse rate and the collapse volume fraction decreased when the foam size decreased,the gas-liquid ratio decreased and the surface tension increased. However, for the larger original volume of foam system, the effect of foam size change on its collapse behaviour was no longer obvious.The collapse rate and the collapse volume fraction increased when the ultrasonic standing wave frequency increased,the amplitude increased and the irradiation time increased.These prediction results were also well validated by ultrasonic defoaming simulation experiments.

(3) Compared with foam size, gas-liquid ratio and surface tension have more significant effect on the decay kinetic characteristics of the foam. Both gas-liquid ratio and foam diameter increased by 40%, the increase of collapse volume fraction caused by the former was 5 times that caused by the latter in the identical irradiation time. Compared with irradiation time, frequency and amplitude of the ultrasonic standing wave have more considerable effect on the decay kinetic characteristics of the foam.Both ultrasonic frequency and ultrasonic amplitude were increased by 50%,the collapse volume fraction of foams increased by about 1.25 times in the identical irradiation time.

Acknowledgements

This work presented in this paper was financially supported by the National Natural Science Foundation of China (Grant No.52174060) and the PetroChina Innovation Foundation (Grant No.2019D-5007-0501). The Postdoctoral Scientific Foundation of Heilongjiang Province in China (Grant No. LBH-Q20012) is also gratefully acknowledged.