Settling behavior of spherical particles in eccentric annulus filled with viscous inelastic fluid

Zho-Peng Zhu , Xin-Zhi Song ,c,*, Ergun Kuru , Hong-Bo Chen , Bu-Wen Yu ,Zi-Cho Lin , Yn-Xin Sun

a China University of Petroleum-Beijing, Beijing,102249, China

b University of Alberta, Edmonton,10230, Canada

c State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum-Beijing, Beijing,102249, China

Keywords:Cuttings transport Particle settling velocity Eccentric annulus Wall effect

ABSTRACT Hole cleaning is a complex process as there are many variables affecting cuttings removal (e.g. drilling fluid type,density,flow rate and rheological properties,cuttings size,drill pipe rotation speed).With the increasing number of drilling small diameter wells (e.g. coiled tubing drilling applications, ultra-deep wells drilled for exploitations of unconventional oil and gas resources), the wall resistance of the micro annulus also emerges as one of the most critical factors affecting the cuttings accumulation in wellbore.The eccentricity of drill pipes commonly observed during the drilling process of ultra-deep well and coiled tubing well makes the wall resistance effect on the cuttings transport even more prominent.Understanding the wall resistance effect on the particle settling behavior in eccentric annuli is,therefore,crucial for hydraulic design of efficient cuttings transport operations in these wells. In this study, a total of 196 sets of particle settling experiments were carried out to investigate the particle settling behavior in eccentric annuli filled with power-law fluids. The test matrix included the eccentricity ranges of 0-0.80,the dimensionless diameter ranges of 0.13-0.75 and the particle Reynolds number ranges of 0.09-32.34. A high-speed camera was used to record the particle settling process and determine the influences of the eccentricity, the dimensionless diameter, the fluid rheological properties, and the solid particle characteristics on the wall factor and the particle settling velocity. The functional relationship among the dimensionless diameter,the particle Reynolds number,and the wall factor was determined by using the method of controlling variables. An eccentric annulus wall factor model with average relative error of 5.16% was established. Moreover, by introducing Archimedes number, an explicit model of particle settling velocity in the eccentric annulus with average relative error of 10.17%was established.A sample calculation of particle settling velocity was provided to show the application of the explicit model.Results of this study can be used as a guideline by field engineers to improve hydraulic design of cuttings transport operations in concentric and eccentric annuli.

1. Introduction

Hydraulic transport of solid particles is a common process encountered in many industrial operations, including transportation of sand particles in oil and gas pipelines and cuttings transport in the drill-hole annulus during oil and gas well drilling(Song et al., 2017). The transport efficiency of the solid particles is crucial for the success of the corresponding industrial processes(Gao et al.,2021;Sifferman et al.,1974).Number of small diameter wells drilled in recent years has been continuously increasing as the industry has been drilling more ultra-deep wells for developing unconventional oil and gas resources (Huang et al., 2021;Shaughnessy et al., 2003) and using coiled tubing drilling technology for the exploration of the low permeability reservoirs(Crabtree, 2020; Hirpa and Kuru, 2020). The increasing drilling depth and the limited drilling fluid circulation rate in the coiled tubing drilling make the cuttings transport and hole cleaning more difficult in these wells (Leising and Walton,1998).

Generally, the borehole sizes encountered in ultra-deep wells and the coiled tubing drillings are significantly smaller than that of the ones in conventional wells (Shi et al., 2018). For example, the small diameter of the coiled tubing is only 4.45 cm,while the more common ones are 6.05, 7.32 and 8.64 cm, and the annular gap width is generally around 2 cm, which makes the annulus wall resistance to cuttings transport non-negligible, further exacerbating the problem of cuttings accumulation in the wellbore(Kamyab and Rasouli, 2016). Drill pipe bending commonly observed in the ultra-deep and coiled tubing drilling process causes the drill pipe to deviate from the central axis of borehole,creating an eccentric annulus and making wall resistance on the eccentric side more severe and complex, even in the vertical well (Ravi and Hemphill, 2006). Cuttings are difficult to be washed due to the low fluid velocity and high cuttings migration resistance in the narrow annulus gap. It is necessary to reveal the state of cuttings migration in the narrow gap of the annulus to ensure that the annulus is completely clean.

Definition of the pipe eccentricity, e, as applied in the drilling operation is given in Fig. 1. First, the central distance (de) was defined as the distance between the centres of the inner and the outer circle.Then the radial difference(Ro-Ri)was used to quantify the size difference between the inner and the outer circles. The eccentricity was then defined as the ratio of the central distance(de)to the radial difference(Ro-Ri)to quantify the deviation of the inner circle from the centre of the outer circle,as shown in Eq.(1).

To quantify the wall resistance effect on the particle settling velocity,the term wall factor,(f),is commonly used.In general,the wall factor (f) is defined as the ratio of the settling velocity of a particle in finite space(vt)to its free settling velocity(v0),(Chhabra et al.,2003).The dimensionless diameter(Dd)is defined as the ratio of the particle diameter to the annular gap size and it is regarded as the most important variable controlling the wall factor(Barati et al.,2014).In addition,the influences of the fluid rheological properties and the particle Reynolds number on the wall factor cannot be ignored(Liu and Sharma,2005; Santander et al., 2021).

Fig.1. Schematic description of an eccentric annulus.

There has been many previous studies of the wall effect (Agwu et al., 2018; Balaramakrishna and Chhabra, 1992; Chhabra et al.,1996; Happel and Bart,1974; Uhlherr and Chhabra,1995). Experiments,numerical simulations and artificial intelligence techniques have been the three most common research methods used for investigating the wall effect on the particle settling behaviour(Agwu et al., 2018). Most of the previous studies investigated the wall effect in circular tubes (Happel and Bart, 1974; Uhlherr and Chhabra, 1995) and reported that the wall factor decreased with the increasing dimensionless diameter (i.e. ratio of particle diameter to that of circular tube). Chhabra et al. (1996) concluded that increasing dimensionless diameter would intensify the wall resistance and, as a result, decrease the particle settling velocity. The transport of proppants and formation sands in fractures is also an important part of any hydraulic fracturing and formation sand control design procedures.In recent years,with the increased use of the hydraulic fracturing technology,more studies have been carried out to investigate the wall effect on the particle transport using parallel plate or vertical fracture geometry (Zhang et al., 2017).

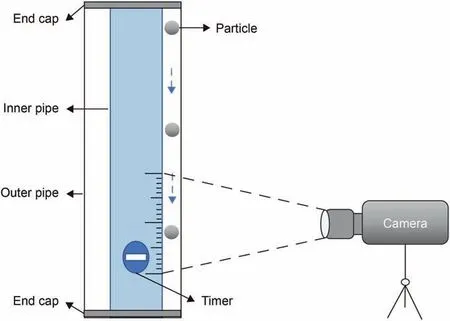
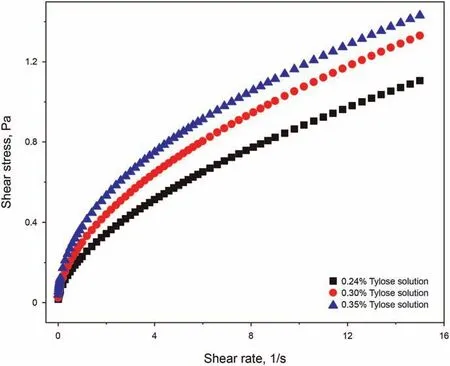
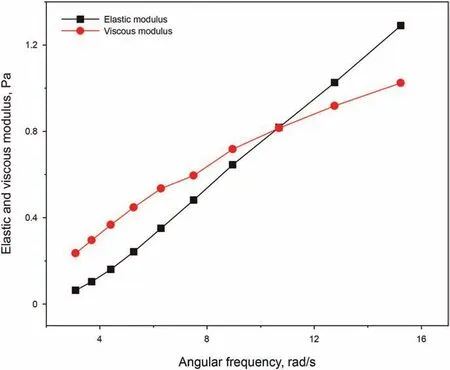
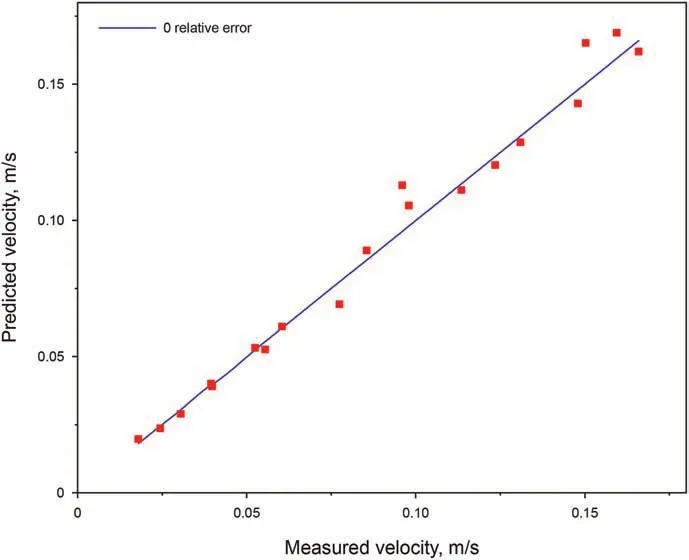
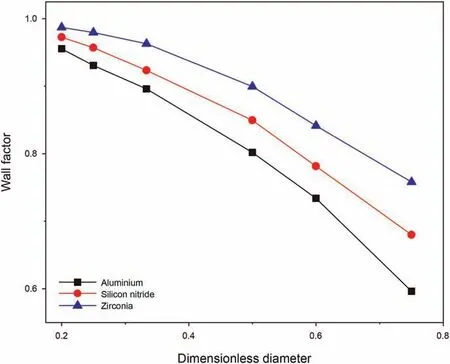
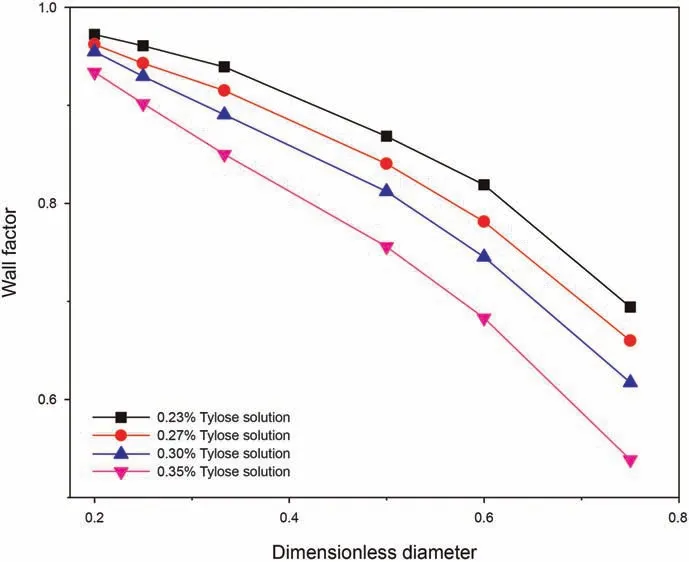
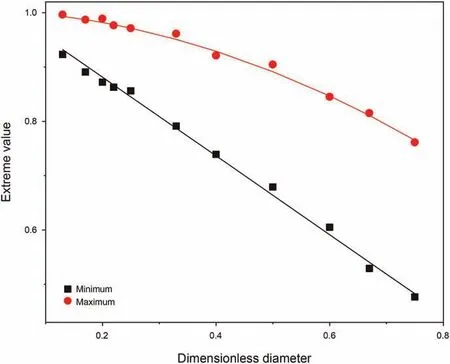
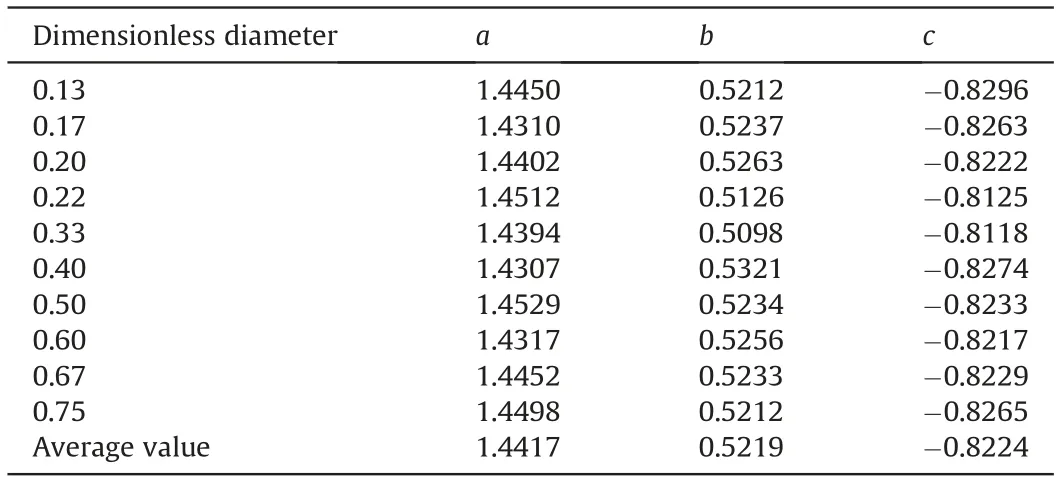
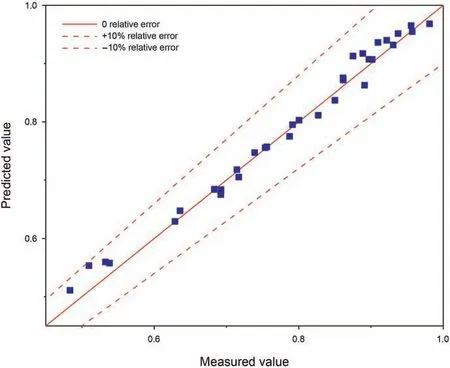
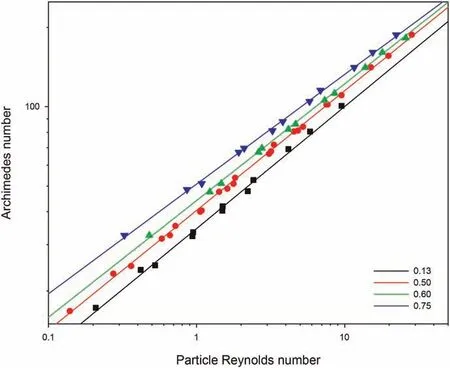
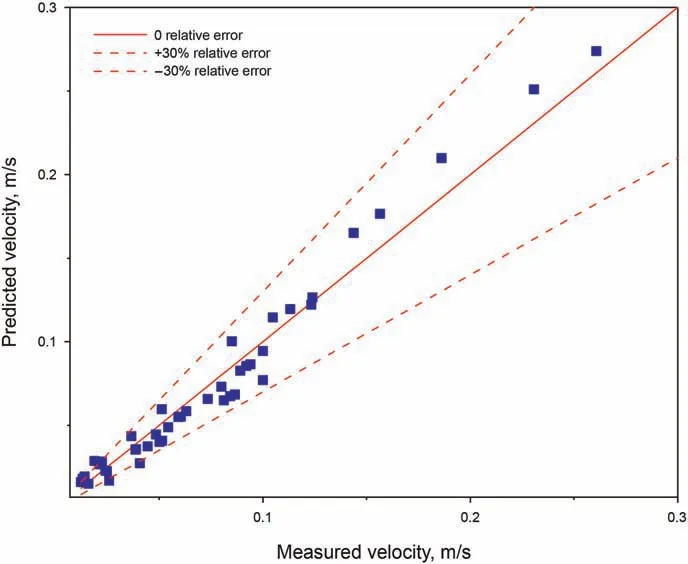
Rheological properties of the fluid(in which the particle settles)are among the important variables that control the wall effect and settling behavior (Liu and Sharma, 2005). The rheological properties of the Newtonian and the Power-law type fluids are relatively simple to characterize and, therefore, they have been commonly used to investigate the wall resistance effect.The particle Reynolds number can be used as criteria to identify the variables controlling the wall factor. At the high (Rep> 150.00) and low range(Rep< 0.50) of particle Reynolds number, the wall factor is only related to the dimensionless diameter.In the middle ranges of the particle Reynolds number(0.50

It is important to note that the wall effect is uniquely related the geometry (i.e. shape and size) of the confining space (Happel and Bart,1974; Yin et al., 2018). Therefore, results of the studies of the wall effect in circular pipe or in fracture geometry(i.e.parallel plate geometry) cannot be extrapolated to the design of the cuttings transport in the annular geometry (Li et al., 2021). To the best of authors' knowledge, the wall resistance in annular geometry as experienced in drilling operations (e.g., narrow annular geometry encountered in coiled tubing drilling and ultra-deep well drilling)has been investigated,but these work didn't consider the influence of eccentric structure on wall effect (Zhu et al., 2022). Due to the difference of geometry, the wall effect of eccentric annulus is not only dependent on its own size.With the increasing eccentricity,it is expected that the wall effect in the narrow side of the annulus will become significant. Therefore, efficient cuttings movement at narrow gaps in the eccentric annulus is essential to annulus cleaning.The main purpose of this study is to reveal the influence of eccentricity on annulus wall effect and provide inspiration for field engineers to optimize hydraulic parameters.Visco-inelastic powerlaw fluids were used as the test fluids.The influence of the elasticity(Arnipally and Kuru, 2018; Bizhani et al., 2016), and the plasticity(Okesanya and Kuru, 2019) of the fluids on the wall effect was not considered for the time being.In addition,although multi-particle deposition is more consistent with the cuttings migration process(Qi, 2001), this study is not concerned with multi-particle deposition because it focuses on the wall effect of eccentric annulus.According to the distribution of flow field in the annulus,the cuttings migration process and wellbore cleanliness can be revealed by accurately calculating the particle settling velocity in the eccentric annulus.

In this study,a total of 196 sets of particle settling experiments were carried out to investigate the particle settling behavior in eccentric annulus filled with power-law fluids. It is worth noting that, considering the feasibility of the experiment, this study only analyzed the influence of the narrow side wall of the eccentric annulus on particle settlement,and this position is representative.Effects of the drill pipe eccentricity, the dimensionless diameter and the particle Reynolds number on the annulus wall effect were analyzed by using the method of controlling variables.By using the data measured under different pipe eccentricity conditions, we have developed a model that can be used for the prediction of the annulus wall factor.In addition,an explicit model for predicting the particle settling velocity in an annulus was developed by introducing the Archimedes number, which is a dimensionless parameter independent from the particle settling velocity. The results of this study can be used as practical guidelines when developing hydraulic design programs and evaluating the occurrence of cuttings accumulation for effective cuttings transport in microboreholes under eccentric drill pipe conditions.

2. Experimental

2.1. Equipment

A high-speed camera and the eccentric plexiglass wellbore are the main components of the experimental set-up.A picture and the schematic diagram of the experimental set-up are shown in Fig.2.

The transparent set-up,used to simulate the circular annulus,is composed of an inner pipe with an outer diameter of 3.00 cm and an outer pipe with an inner diameter of 6.00 cm. Both cylindrical pipes have a wall thickness of 0.50 cm. The height of the column was 60 cm.

The observation area was located 20 cm below the top surface and 10 cm above the bottom surface of the column.The observation area was equipped with a ruler for measuring the distance covered by the settling particle with an accuracy of 1 mm.A timer with an accuracy of 0.01 s was used for recording the corresponding settling time. The camera positioned 50 cm away from the eccentric annulus was facing the observation area laterally to ensure that the shooting angle was 90°to the direction of the particle settling.The camera's shooting frequency was 100 frames per second, which further ensured the accuracy of velocity measurements.

Fig. 2. Experimental set-up.

Note that particles were dropped into the narrow side of the eccentric annulus. In this way, the maximum gap width for the settling velocity in this experiment was equal to the gap width of the concentric annulus (1.5 cm). Using 3D-printing technique, we have prepared seven sets of end caps that can be used to adjust inner pipe eccentricity.Images of these end cap samples are shown in Fig.3.The end cap positioned at the top was also equipped with a small circular hole allowing the user to drop the particles from the same position consistently. The corresponding end cap with the same orientation as the top one is mounted at the bottom of the annular vessel.

For each pre-set eccentricity, the corresponding end caps are respectively placed in the upper and lower ends of the outer pipe and the inner pipe was secured at the desired eccentricity position.With these eccentric end caps, we can vary eccentricity from 0 to 0.80 with the corresponding range of gap width 0.30-1.50 cm, as shown in Table 1.

2.2. Materials

Three types of spherical particles were used in the experiments namely, aluminium (Al), silicon nitride and zirconia (Zr). Particle density varied from 2700 to 6000 kg/m3. In addition, in order to quantitatively evaluate the wall resistance in the eccentric annulus within a wider range of particle Reynolds number, two different particle sizes were used. The detailed physical properties of the particles are summarized in Table 2.

Tylose polymer, a derivative of carboxymethyl cellulose (CMC),was used for preparing viscous fluids tested in the particle settling experiments. Tylose is often used as a thickener and/or a texture ingredient in many applications in the food service industry.Aqueous Tylose solutions of different mass concentrations were used as test fluids.Accurate measurements of the fluid rheological properties are needed to develop realistic models describing the particle settling behaviour. Fluids formulated by using Tylose polymer exhibit a shear thinning power-law characteristic. The rheological properties of the test fluids were measured by using the stress-controlled mode of C-VOR rheometer from Bohlin Instruments with 40 mm and 4°cone and plate geometry. All the measurements were conducted at 21°C.The diameter of the fixed bottom plate was 60 mm,and the gap between the cone and plate was 150 μm.The rheological characteristic curves of the fluids used for the experiments are shown in Fig. 4.

Fig. 3. Examples of the end caps used for controlling the inner pipe eccentricity.

Table 1 The eccentricity and corresponding gap width values of the annular geometry.

Table 2 The properties of the test particles.

Fig. 4. Rheological characteristic curves of Tylose solutions.

The results showed that with the increasing polymer mass concentration, the consistency index (K) of Tylose solutions also increased and the flow behaviour index (n) decreased indicating that the shear thinning property was slightly enhanced while fluids were exhibiting more non-Newtonian characteristics.In addition to measuring their viscometric properties, we have also determined the elastic properties of the Tylose solutions to confirm that test fluids do not exhibit any significant elasticity. To determine the elasticity of the test fluids, we used stress-controlled mode of CVOR rheometer from Bohlin Instruments with 40 mm and 4°cone and plate geometry.The storage modulus,Gʹ,denotes the solid-like behaviour of the material, and the loss modulus, Gʺdenotes the liquid-like behaviour of the material when a sinusoidal form of deformation is applied.The frequency at which Gʹand Gʺbecomes equal has a physical significance,and that frequency is called cross over frequency.The inverse of the crossover frequency provides the longest relaxation time of the material. The relaxation time is defined as the time needed for any deformed material to regain its original structure. The elasticity of a material can be quantified by its relaxation time (Arnipally et al., 2018; Malhotra and Sharma,2012). Generally, longer the relaxation time is, the more elastic the material will be. An example of such characteristic plot for 0.30 wt% Tylose solution is shown in Fig. 5.

Measured relaxation time of these Tylose solutions were very low indicating that Tylose solutions under the investigation could be considered as inelastic fluids for all practical purposes.Summary of the rheological properties is given in Table 3.

Fig. 5. Elastic and viscous moduli of 0.30 wt% Tylose solutions.

2.3. Methodology used for ensuring data quality and repeatability

Following a precisely controlled methodology is important to minimize the experimental error. In this study, several measures were taken to ensure the quality and repeatability of the measured data.The test fluids were prepared 12 h before the experiments and kept at rest in the annular test column allowing micro bubbles to escape out.Meanwhile,the solid particles were soaked in the same test fluid to eliminate the interference of surface forces between particles and test fluid. Due to the narrow space of the eccentric annulus, obtaining a fully vertical annulus was essential to effectively reduce the collision between the settling particle and the inner wall of the annulus. Here we used a horizontal gauge to ensure that the annulus column was vertical.In addition,a special particle gripper was used to release particles. It should be noted that only one particle was dropped at a time(in each test)to avoid collision between particles. With the help of a special gripper, the release position of particles was set below the liquid level and the particles fell vertically without having an initial velocity. The observation area was set 10 cm above the bottom surface of the test column and 20 cm below the top surface of the fluid column.In this way,we could ensure that the particle reached the terminal settling velocity in the observation area and also avoid the end effects of the vessel. In general, we took a contrast method to determine the terminal settling velocity. The observation area was divided into three identical areas,and the average velocities in these three areas were compared. If the error between the three average velocities was less than 5%, the particle was considered to have reached the terminal settling velocity. If the particles cannot reach the final velocity, the upper boundary of the observation area can belowered to increase the settling distance. To minimize the measurement error, each particle settling test was repeated five times while making sure that at least three measurements with a variation of less than 5%were obtained,and the average value was taken as the test result.

Table 3 Properties of the fluids used for model development and verification.

2.4. Experimental validity

To ensure the accuracy and effectiveness of the experiment,the free settling velocity of particles in the test fluid was measured before the experiment, and the measured results were compared with the previous research. Shah et al. developed a more generalized prediction model for the sedimentation velocity of particles in a power-law fluid (Shah et al., 2007). As shown in Fig. 6, the test results have a good fitness with the study by Shah et al.,the average relative error is only 6.83%. Therefore, we can confirm the measurement accuracy and validity of this experiment.

3. Experimental results

3.1. Particle settling velocity

As shown in Fig.7,the settling velocities of aluminium particles in the 0.30 wt% Tylose solution decreases monotonically with the increasing dimensionless diameter.In Fig.7,the slope of the trend lines of 3-mm and 2-mm particles are 0.050 and 0.018,respectively,indicating that the settling velocity of large-diameter particles decreases more significantly.With the increasing eccentricity of an annulus,the annular gap width decreases(dimensionless diameter increases),which in turn,causes the wall resistance also to increase.As discussed earlier, increasing wall resistance would retard the settling velocities of the particles in the annulus.

Variation of the particle settling velocity with the increasing eccentricity is shown in Fig. 8. The relationship between the eccentricity and the settling velocity is not linear.The particle settling velocity decreases at a slower rate within the small eccentricity range. However, the reduction rate of the settling velocity accelerates as the eccentricity becomes larger than some critical value.

Note that in these experiments, the particles were dropped in the narrow side of the annulus(see Fig.3).Results shown in Fig.8 indicate that as the eccentricity increases (i.e. gap width in the narrow side decreases and the wall effect increases) the settling velocity of the particles in the narrow side of the annulus decreases.Decreasing settling velocity means cuttings may be transported more effectively in the narrow side of the annulus. However, in reality,the fluid velocity in the narrow side of the annulus will also decrease as the eccentricity increases.The net transport velocity of the cuttings is simply the difference between the fluid velocity and the particle settling velocity. In other words, the net transport velocity of the cuttings will be a function of relative changes in both the fluid velocity and the particle settling velocity due to eccentricity. Therefore, it is not straight forward to predict the overall impact of the increasing eccentricity on the particle transport efficiency in the narrow side of the eccentric annulus.

Fig. 6. Validation of measurement accuracy by comparing with Shah et al. (2007).

Fig. 7. The relationship between the dimensionless diameter and the setting velocity of 2-mm and 3-mm aluminium particles in 0.30 wt% Tylose solution.

In reverse reasoning, the settling velocity of particles in the wider side of the eccentric annulus(where the gap width increases due to eccentricity, and hence, dimensionless diameter and wall resistance decrease) will be on the high side and will not change significantly,as shown in Fig.7.The fluid velocity in the wider side of the eccentric annulus is generally higher than that of the narrow side. Here as well, the net velocity of the cuttings transport would be a function of the relative changes in fluid and particle settling velocities. Therefore, it is not a trivial task to predict the overall impact of the increasing eccentricity on the cuttings transport efficiency in the wider side of the eccentric annulus either.

Fig. 8. Change in particle settling velocity with the increasing drill string eccentricity for 2-mm and 3-mm aluminium particles in 0.30 wt% Tylose solution.

3.2. Wall factor

Unlike the motion of solid particles in an infinite space, the transport of solid particles in finite space is hindered by the confining boundaries.In this study,we also used the wall factor to evaluate the influence of the wall resistance of the eccentric annulus on the particle settling velocity. Although there is a common consensus that the wall factor is mainly controlled by the dimensionless diameter,the effects of particle and fluid properties on the wall factor cannot be ignored.

Fig. 9. The effect of particle density on the wall factor in the in 0.30 wt% Tylose solution with K = 0.35 Pa sn and n = 0.54.

Results shown in Fig.9 indicate that the denser particles have a larger wall factor,i.e.,the retarding effect of the wall on the particle settling velocity becomes weaker as the particle density increases.Denser particles settle at higher velocities, resulting in higher interlaminar shear rates in the surrounding fluid. Considering the shear thinning characteristics of the test fluid,the increasing shear rate results in a decrease in the fluid apparent viscosity, the wall resistance to the high-density particles is relatively reduced. Results from previous studies of the effect of shear thinning of the fluid on the wall effect are also in line with these findings(Missirlis et al., 2001; Song et al., 2009).

As shown in Fig. 10, as the fluid viscosity increases, the wall factor decreases (i.e. resistance effect of the wall on the particle settling velocity increases).

The terminal settling velocity of the particle is controlled by the balance between the net weight force of the settling particle (i.e.the difference between the force of gravity and the buoyancy force)and the viscous drag force of the fluid moving around the settling particle. Therefore, when the net weight force remains constant(i.e. for a given particle size, density and fluid density), an exact drag force is needed to satisfy the force balance.The fluid drag force is a function of the fluid viscosity and the velocity.Therefore,as the fluid viscosity increases, a smaller settling velocity is needed to satisfy the force balance. The wall factor will decrease with the increasing fluid viscosity.

The relationship between the wall factor and particle Reynolds number is shown in Fig. 11. In general, the particle Reynolds number (Rep) in power-law fluids can be expressed as follows:

where K and n are the consistency index and flow behavior index of a power-law fluid respectively;ρpand ρfare the particle density and the fluid density, respectively; dpis the particle diameter; g is the gravitational acceleration; v is the settling velocity of the particle.According to the defining expression of the particle Reynolds number, different particle Reynolds numbers with the same dimensionless diameter can be obtained by changing the particle diameter, the density and the rheological parameters of the fluid.The particles with larger diameter and the density settling in the fluid with lower viscosity usually corresponds to a larger particle Reynolds number. The wall factor increases significantly with the particle Reynolds number within the middle range of particle Reynolds number (i.e. Rep～ 1-10). Outside the middle range, the influence of the particle Reynolds number on the wall factor is not significant,especially for dimensionless diameter values lower than 0.5.

Fig.10. The effect of viscosity on the wall factor of 3-mm silicon nitride particles.

Fig. 11. The relationship between the wall factor and the particle Reynolds number(Given for dimensionless diameter values of 0.13, 0.22, 0.33, 0.50, 0.67).

The relationship between the wall factor and the particle Reynolds number further confirms the individual effects of the particle density and the fluid viscosity discussed earlier.The relationship of the wall factor and particle Reynolds number presented in this study is also in line with the results from similar studies conducted previously(Chhabra and Peri,1991; Song et al., 2019).

4. Model development for wall factor and particle settling velocity

Based on the relationship between the eccentric annulus wall factor, the dimensionless diameter and the particle Reynolds number,an empirical model of the wall factor was established.An explicit model for the prediction of the particle settling velocity in the eccentric annulus was also developed. Here, the least square curve fitting method was used to match the trend lines of the experimental results. Note that four fluids (i.e. 0.24, 0.27, 0.30,0.35 wt% Tylose solutions) shown in Table 3 were used to develop the wall factor model and settling velocity model,and the fifth fluid(i.e. 0.33 wt% Tylose solution) was used to verify the established models to ensure the generalization ability and the credibility of the models.

4.1. The wall factor model for particle settling in an eccentric annulus

Experimental results have shown that the wall factor in the eccentric annulus generally increases with the increasing particle Reynolds number (Fig.11). Similar trends of the wall factor versus the particle Reynolds number were observed at different dimensionless diameters. For each dimensionless diameter value, when the particle Reynolds number was less than about 1,the wall factor has a minimum value (f0); when the particle Reynolds number is greater than about 10, the wall factor has a maximum value (f∞)(Fig. 11). Therefore, as a first step of establishing the wall factor model, we needed to determine these extremum values under different dimensionless diameters.Statistical analyses showed that extreme values of the wall factor decreased with the increasing dimensionless diameter,and the difference between the maximum and the minimum values became more distinct (Fig.12).

As the dimensionless diameter increased from 0.13 to 0.75, the difference between the maximum and minimum values of the wall factor increased by 3.43 times. The main reason is that the wall resistance has more significant impact on the settling velocity with the increasing dimensionless diameter. Moreover, the maximum and minimum values and dimensionless diameters show quadratic polynomial in Eq. (4) and linear relationships in Eq. (5), respectively.The correlation coefficient(R2)was higher than 0.98 in both cases.where Ddis the dimensionless diameter;a,b, c are the correlation coefficients that can be defined as a function of the dimensionless diameter; f∞and f0are the extremum values of the wall factor as defined by the Eqs. (4) and (5), respectively. The least square method was used to curve fit the f vs.Reptrend lines and determine the correlation coefficients a, b, and c at different dimensionless diameter values. The correlations coefficients obtained from curve fitting analyses are summarized in Table 4.

Correlation coefficients of the Eq. (6) do not show significant variation as a function of the dimensionless diameter. Therefore,the average values were taken as the representative values of the coefficients a,b,and c.Finally,an empirical wall factor model for a particle settling in an eccentric annulus is proposed as follows.

Fig.12. Relation between the dimensionless diameter and the extreme values of the wall factor.

Table 4 Coefficients in Eq. (5) evaluated at different dimensionless diameter values.

The data obtained from the tests conducted by using 0.33 wt%Tylose fluid was used to evaluate the predictive ability of the empirical model,as shown in Eq.(7).A comparison of the measured and predicted wall factor values is shown in Fig. 13. The average relative error between the model predictions and the actual measured values of the wall factor was only 5.16%.

4.2. An explicit model of the particle settling velocity in an eccentric annulus

Although the wall factor model can quantify the wall resistance of the annulus on the particle settling velocity,it cannot be used to predict the particle settling velocity. An explicit model for predicting particle settling velocity is necessary in this case.

Previous studies focused on determining an empirical relationship between the particle drag coefficient and the Reynolds number, and then determining the settling velocity by using an iterative trial and error process. However, from a practical field application point of view, an explicit model allowing the direct prediction of the particle settling velocity is preferred.Therefore,an explicit model for predicting the particle settling velocity in the eccentric annulus is presented here.

Chhabra and Peri(1991)proposed to use Archimedes number to establish an explicit model that could be used to predict the free settling velocity of a particle,where the test fluid was also a powerlaw type. More recently, Qingling et al. (2018) proposed a similar method for determining the free settling velocity of particles explicitly. In this study, we have adopted the same methodology proposed by Qingling et al. (2018) to develop an explicit model to determine the settling velocity of particles in the eccentric annulus.

Fig.13. Comparison of the model predictions and measured values of the wall factor.

First step of the method is to determine the dimensionless variable,Archimedes number(Ar),which is a combined function of the drag coefficient and the particle Reynolds number (Chhabra and Peri,1991) as shown in Eq. (8):

A total of 196 sets of particle settling experiments were carried out to reveal the particle settling behaviour in the eccentric annulus filled with power-law fluids, involving the eccentricity range of 0-0.80, the dimensionless diameter range of 0.13-0.75 and the particle Reynolds number range of 0.09-32.34. Based on the experimental results, a plot of Archimedes (Ar) number versus particle Reynolds number (Rep) for different dimensionless diameters was developed, as shown in Fig.14.

A plot of Ar vs.Repdata in the logarithmic scale yielded unique trend lines distinguished from each other depending on the dimensionless diameter. A linear relationship in logarithmic scale indicates that a power law relationship between Ar and Repcan be suggested as follows:

where A and B are the correlation coefficients that can be defined as a function of the dimensionless diameter(Dd).

Fig.14. The relationship between the Archimedes number and the particle Reynolds number for the dimensionless diameter of 0.13, 0.50, 0.60, and 0.75.

Further analyses shown in Fig.15 revealed that the correlation coefficients A, B and the dimensionless diameter, Dd, exhibited a polynomial and a linear relationship with the correlation coefficients (R2) of 0.96 and 0.94, respectively. The resultant expressions for the correlation coefficients A and B are given by Eqs.(12)and (13) as follows:

Eqs. (11)-(13) describe the empirical relationship between Ar and Rep. As shown in Fig. 15, the model predictions show an excellent fit to the experimental data with an average correlation coefficient (R2) higher than 0.95 for various dimensionless diameters.

Finally, by combining Eqs. (9) and (11)-(13), and taking the particle settling velocity, v, out of the combined expression, an explicit equation for predicting the particle settling velocity in an eccentric annulus was developed as follows:

Fig. 15. Functional relationship between the correlation coefficients A, B and the dimensionless diameter Dd.

Fig.16. Comparison of the measured and predicted particle settling velocity values in the eccentric annulus.

Experimental dataset obtained by using 0.33 wt% Tylose fluid were used to evaluate the prediction accuracy of the explicit model of the particle settling velocity. As shown in Fig. 16, the average relative error of the model predictions using Eq. (14) was 10.17%and the maximum relative error was 23.19%.

4.3. Sample calculation of the particle settling velocity in an eccentric annulus

Particle and fluid properties are summarized in Table 5. The annular geometry corresponding to this case is defined by the inner diameter(di) of 3 cm, the outer diameter (do) of 6 cm, and the eccentricity (e) of 0.40.

Following stepwise procedure was used for the calculation of the particle settling velocity:

(1) Determine the gap width,w, of the eccentric annulus:

5. Conclusions and recommendations

In this study,196 sets of particle settling velocity experiments were carried out to investigate the settling behavior of particles in an eccentric annulus filled with power-law type fluids. Theexperimental program was designed by considering the annulus eccentricity range of 0-0.80, the dimensionless diameter range of 0.13-0.75,and the particle Reynolds number range of 0.09-32.34.A wall factor model and an explicit particle settling velocity model were established for particle settling in an eccentric annulus.Based on the results obtained from this study, following conclusions can be offered:

Table 5 Fluid and particle properties used for the case study.

(1) Under the same cuttings transport condition, the wall effect on the particles with the higher density or the larger diameter will be more dominant.

(2) The wall factor in the eccentric annulus is a function of the dimensionless diameter and the particle Reynolds number.It decreases with the increasing dimensionless diameter, and increases with the increasing particle Reynolds number within the Reynolds number range of 1-10.

(3) With the increasing drillstring eccentricity, the particle settling velocity decreases at an accelerated rate.

(4) The settling velocity of the particles in the broader side of the eccentric annulus will not be significantly affected by the wall effect, while the settling velocity of the particles in the narrow side of the annulus will be reduced significantly.However, the overall efficiency of the particle transport in the eccentric annulus will be a function of both the fluid velocity (which is significantly lower in the narrow side of the eccentric annulus) and the particle settling velocity.

(5) As for the future work, the cuttings transport behavior of more complex cases such as settling behaviour of multi particles in the inclined and horizontal annulus can be investigated by using numerical simulation and artificial neural network techniques.

Acknowledgments

Authors express their appreciation to the Strategic Cooperation Technology Projects of CNPC and CUPB (ZLZX2020-03), and China Scholarship Council (201906440166) for their financial support.Authors would also like to acknowledge financial support provided by the Natural Sciences and Engineering Research Council of Canada(NSERC RGPIN-2016-04647 KURU).Authors would like to thank Dr.Xinxiang Yang of the University of Alberta for his assistance and support in carrying out this study.