政策工具视域下体育大数据产业模型构建与选择评价

陈海珊 张艺 董琛

(山东体育学院体育社会科学学院 山东济南 250102)

在体制改革和制度创新过程中，无法否认这样一个事实：几乎所有的体制改革和制度创新都需要具体化为一系列的相关政策，而各种具体政策都需要选择恰当的政策工具，才能得到良好的执行并保证达到事先预设目标，以避免在政策层面出现“执行走样”或“无力”的局面，体育大数据改革同样如此。体育大数据产业具有绿色、健康和高附加值等重要属性，对GDP、财政收入增长及社会发展起到至关重要的作用。然而，体育大数据产业只是区域可持续发展系统的一个子单元，如何规划体育大数据产业发展，作为新的经济增长点嵌入当地社会、经济和环境可持续发展系统中，成为体育大数据产业发展需要研究的关键。体育小镇建设方兴未艾，挑战与机遇并存，该研究将以新兴的体育小镇为例，通过建立体育大数据产业的系统动力学模型，来表达体育大数据产业与当地社会、经济和环境发展之间的相互关系与相互作用，不是将它看作一个独立分割的单元，而是将它作为整个小镇发展的有机组成成分，它与其他子系统互为因果，反馈协作，共同驱动体育大数据产业及整个小镇的可持续发展，预测和评估21世纪中叶体育大数据产业的发展。

1 模型前提条件和参数确定原则

1.1 前提条件

该研究的体育大数据产业系统动力学模型主要建立在以下5个前提与假设基础之上。

（1）由于模型所研究的只是一个较小的区域——体育小镇范围，因此所有的状态变量、速率变量及参数都可以看作是集中参数，它们的值只随着时间发生变化，而与空间分布无关。

（2）模型中变量之间相互影响、相互作用，共同驱动着系统的发展方向，变量之间的相互联系是它们变化（导数）发生的原因。

（3）在模型的仿真区间（2018—2050年）内，体育小镇不会发生重大自然或社会灾害，即不会发生因系统内部或外部扰动导致的消失没落现象，各个状态变量、速率变量和参数都在可以接受的范围内变化。

（4）在模型的仿真区间（2018—2050年）内，该地区可持续发展结构包括经济、人口和自然环境等保持相对稳定。模型的结构是有效的，模型的解反映了体育大数据产业系统的动态只由模型参数决定，而与模型的结构无关，也就是驱动系统运行的动力学原理是恒定的。

（5）政府相关部门能够准确地得到系统状态变量及其组合的反馈信息，并具有改变模型政策参数，从而改变体育小镇发展动态的执行能力。

1.2 变量参数的确定原则

因为与体育大数据产业发展相联系的方面非常广泛，相互关联组成的结构也非常复杂，所以需要较多的变量才能描述这样的巨系统。但是若选择过多的变量去描述系统，那么会导致模型异常复杂，变量之间的相互关系通常具有时变、非线性的特点。研究在保证关键信息完整和模型预测精度的前提下，尽可能地选择较少的变量去描述系统的变化，并简化它们之间的相互关系与作用，也就是建立一个简而明的系统动力学结构。该文采用的筛选变量和参数主要原则有五项。

1.2.1 目标原则

从哲学上说，系统是无限可分的，需要用无数个变量去描述一个动态系统，但在实际当中是不可能的，人们总是有自己的目的。因此，该研究在选择状态变量时，充分考虑它们是否有利于研究目标的实现，系统分析直到能够解决问题的那一层次为止。

1.2.2 简化原则

对不产生重要非线性关系的变量可以省略不计，如可以不关心每年用于科技经费的具体数额，只要知道每年政府财政的投资系数（政策参数），就知道每年有多少经费用于科技研发，这样只用1个状态变量（政府财政收入），就可以描述GDP因科技投入产生变化的动力学原因。同时，进行简化的还有变量之间的相互关系，这些关系往往是非线性的，尽管它们是产生速率变量（导数）的动力学原因，但为了便于分析与计算，把有些关系简化为简单的线性或非线性回归关系。

1.2.3 反馈原则

该研究的研究对象——体育大数据产业系统模型是边界闭合的，也就是说变量与变量之间的关系是相互关联、互为因果，最后反馈到起点的，反馈环在可持续发展中是普遍存在，并且起着非常重要的作用。因此，该研究在确定状态变量时，高度重视具有反馈作用的变量，由它们之间的相互关系组成闭合的或大或小的反馈环，重要的政策参数都设计到这些反馈环上，增加参数的敏感性和有效性。

1.2.4 意义明确原则

变量通常是质和量的统一体，它不是抽象无意义的，而是意义明确具体，可量化可操作的。因此，在确定变量时，选择意义明确、量纲量级完整，具有较强可实现可制作的变量，作为模型的状态变量或评价指标。

1.2.5 最小集合原则

变量选择力争做到不重复、不遗漏，保证用最小的状态变量集就可以描述体育大数据产业系统动态变化过程，模型中的一切速率变量和参数或是常数，或是这些状态变量的函数。

2 体育大数据产业可持续发展系统动力学模型

2.1 系统分割与过程假定

系统模型只能反映真实系统某一层次或某一方面的动态，以及导致这种动态的动力学机制。但它还远不是真实系统原型本身，只是为了解决某个研究问题而创建的真实系统原型的相似物。因此，为了实现研究目的，必须对体育大数据产业系统进行合理的简化，抓主放次，将系统划分为若干单元，它们有机联系，自下而上地组成整个系统的结构。该研究把体育大数据产业系统中涉及的经济、社会和环境视为3 个相对独立，同时又有紧密联系的子系统。通常采用状态变量描述系统某一方面的变化，经严谨的系统分析，确定系统动力学最简模型应有7 个状态变量，由它们构成的集合（状态空间），可以描述系统的结构以及由结构导致的所有复杂动态行为。由于该研究的对象是体育小镇的产业发展规划，因此第一个状态变量是该小镇的体育大数据产业产值（x：万元）。下面依次介绍其他子系统包括的状态变量。

2.1.1 经济子系统

采用两个状态变量描述，分别是GDP（x：万元）和财政收入（x：万元）。这两个变量可以充分描述体育小镇经济发展的状态。经济的发展是体育大数据产业发展的源动力，由GDP的增长可以导致财政收入的增长，财政对体育大数据产业的直接投入可以快速促进其发展，同时对教育和科技研发的投入也能间接地导致体育大数据产业的健康快速发展。

2.1.2 社会子系统

采用两个状态变量描述，分别是人均年收入（x：万元）和人口数量（x：万人）。社会子系统非常复杂，但该研究选取与体育大数据产业最直接的社会单元作为状态变量，同时它们与其他子系统关系密切。例如，体育大数据产业的繁荣可以提高人口素质，降低死亡率，从而导致人口增长。人口及人口素质提高会对GDP增长产生积极作用，从而提高财政收入和人均年收入，政府会有更多的经费用于投资教育、研发和体育大数据产业发展，同时人们会有更多的钱用于体育消费，从而反过来进一步促进了体育大数据产业的发展。

2.1.3 环境子系统

采用两个状态变量描述，分别是当年用水量（x：万吨）和当年发电量（x：万度）。体育小镇发展最重要的目标是保护资源与环境，让经济、社会发展与资源环境保护协调一致。因此，该研究选取当地最重要的环保指标——水资源环境利用程度和燃烧煤炭的发电量作为状态变量，体现对资源与环境的保护。这两个状态变量与其他子系统的状态变量是密切联系的，例如，耗水和耗电量直接决定GDP 的增长，而财政投入导致的科技进步又能够提高用水用电的功效，减少单位GDP的能耗与水耗，从而有效地保护资源与环境。

2.2 体育大数据产业可持续发展系统内部关系流程图

经过以上分析，可以确定各个子系统之间的相互关系，从而建立系统内部关系流程图（见图1）。

图1 中包括所有的状态变量，以及它们之间的相互关系和相互作用，这样的结构产生了驱动系统运行的动力学机制——速率变量，以及调节速率变量的系统参数和政策参数。图中包括4 条主反馈环，它们从根本上决定了系统的发展变化动态，具体如下：

图1 体育大数据产业系统内部结构关系

（1）GDP（x：万元）→财政收入（x：万元）→人口素质（占总人口的比例）→GDP。

（2）体育大数据产业产值（x：万元）→人口数量（x：万人）→人均年收入（x：万元）→体育大数据产业产值（x：万元）。

（3）GDP（x：万元）→财政收入（x：万元）→科技投入（占财政收入的比例）→当年用水量（x：万吨）→GDP（x：万元）。

（4）GDP（x：万元）→财政收入（x：万元）→科技投入（占财政收入的比例）→当年发电量（x：万度）→GDP（x：万元）。

这4 条主反馈环决定着系统动力学模型的解，即系统动态。所有政策参数都设计在这4 条主反馈环上，具有较强的参数敏感性，这样的模型设计极大地提高了系统模型与实际原型之间的结构与功能相似性。

2.3 模型的速率变量

速率变量及速率方程是系统动力学建模的核心，速率就是导数，由于导致状态变量发生变化的原因不止一个，为了区别，用速率表示状态变量总导数构成的某一个分导数。如前所述，状态变量的导数可以表示成所有引起改变的速率变量的代数和，而每一个速率又可以表示成状态变量与系统参数的函数。因为速率是关系和作用的产物，没有状态与状态之间的相互关系和相互作用，就不存在由此引起的速率，而系统参数起到调节速率大小的作用，它对状态的影响是通过调节速率对时间的积分间接实现的。下面对体育大数据产业系统动力学模型中的相关速率详细进行说明。

2.3.1 与体育大数据产业产值（）有关的速率变量及速率方程

与有关的速率变量如下：

（1）：每年财政收入拨付给体育大数据产业的经费（万元），=，其中为体育大数据产业拨款占总财政收入的比例（%）。

（2）：每年人均用于体育的花销（万元），=，其中为人均用于体育的花销占人均收入的比例（%）。

（3）：每年大专及以上人口的数量（万人），=，其中为大专及以上人口占总人口的比例（%）。不是一个定值，它与财政对教育的投入有关，根据文献研究，它可以表示为：

（4）：每年财政收入对科技的投入（万人），=，其中为对科技研发投入占总财政收入的比例（%）。

其中，表示科技进步对体育大数据产业产值增长的贡献系数。因此，体育大数据产业产值（）变化的一阶动力学模型为：

其中，μ表示体育大数据产业产值的最大比增长速率；表示体育大数据产业产值增长对财政拨款的依赖系数（万元）；表示体育大数据产业产值增长对人均体育花销的依赖系数（万元）；表示体育大数据产业产值增长对人才的依赖系数（万人）。

2.3.2 与GDP（）有关的速率变量及速率方程

与有关的速率变量是GDP 的年增长速率，它与状态和，以及有关，因此（，，），同样可以表示为：

其中，表示GDP 的最大比增长速率，、和分别表示GDP的增长对人口素质（大专及以上学历人口）的依赖系数（万人），对水资源的依赖系数（吨/万元）和对电能的依赖系数（度/万元）。因此，GDP（）变化的一阶动力学模型为：

2.3.3 与财政收入（）有关的速率变量及速率方程

与有关的速率变量如下：

（1）：财政收入的增长速率，它与GDP 的增长密切相关，可以表示为=，其中表示财政收入占GDP的比例（%）。

（2）：财政收入的投资速率，可以表示为=，其中表示财政收入的投资系数。

因此财政收入（）变化的一阶动力学模型为：

2.3.4 与人均年收入（）有关的速率变量及速率方程

2.3.5 与人口数量（）有关的速率变量及速率方程

与有关的速率为：

（1）人口的出生速率，它包括人的自然出生速率，以及由于体育大数据产业发展驱动的健康水平提高对人口的出生速率的贡献，因此可以表示为：

其中，表示人口自然出生率，表示体育大数据产业发展水平的提高对人口出生率的贡献系数。

（2）人口的死亡速率，它包括人的自然死亡速率，以及由于体育大数据产业发展驱动的健康水平提升对降低人口死亡率的贡献，因此可以表示为：

其中，表示人口死亡率，表示体育大数据产业发展水平对降低人口死亡率的贡献系数。因此人口数量（）变化的一阶动力学模型如下：

2.3.6 与当年用水量（）有关的速率变量及速率方程

与有关的速率是当年用水增长速率，它与有关，可以表示为=，其中表示每产生单位GDP 的耗水系数（吨/万元），然而不是定值，它与科技进步呈指数负相关，在GDP发展的过程中科技含量越高，越小。因此它可以表示为（），即=，其中ε是指数回归系数，表示最大单位GDP 耗水系数。因此当年用水量（）变化的一阶动力学模型如下：

2.3.7 与当年发电量（）有关的速率变量及速率方程

与的动力学模型类似，与有关的速率是当年发电量增长速率，它也与有关，可以表示为=，其中表示每产生单位GDP 的耗电系数（度/万元），同样也不是定值，它与科技进步亦呈指数负相关，在GDP 发展过程中科技含量越高，值越小。因此，它也可以表示为（），即=，其中ζ 是指数回归系数，表示最大单位GDP 耗电量系数，因此，当年用电量（）变化的一阶动力学模型如下：

基于此，系统动力学模型可通过如下关于状态变量的一阶常微分方程组进行描述，见公式13～19。

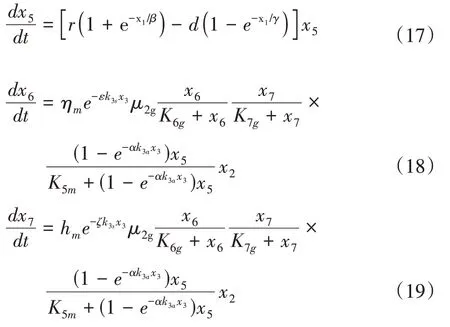
该模型是非线性的，不存在解析解，只能通过计算机仿真实验获得它的数值解，以此对系统的动态进行定量分析与研究。

3 模型的参数辨识及有效性检验

3.1 新兴体育小镇基础数据调查

该研究根据新兴体育小镇相关部门（发改委、统计局和环保局等）的权威统计资料，获得从2007—2017年关于模型中7个状态变量和相关可调节政策参数的调查值（表1、表2）。

表1 新兴体育小镇2007—2017年区域发展状态变量

表2 新兴体育小镇2007—2017年区域发展政府可控制参数

由于新兴体育小镇目前的体育大数据产业为初创阶段，产值几乎为0，模型中与之有关的参数设置为0，而其他政策参数则采用该地区在发展过程中的实际调查值。

3.2 基于样条插值的数据量扩增

由于状态变量的调查数据只有11 组，无法满足参数辨识和有效性检验要求的数据量，因此研究采用B样条函数插值的方法在调查数据内部的各个时间上进行内插值，生成数量较多的数据用于数学建模。在各个状态变量的采样时间（1 年）内生成365 个插值时间点，共生成4015个内插点，各个状态变量内部时间点的插值结果，如图2 所示。可以看出该11 个数据生成了一条平滑的插值曲线，即基于11个数据得到了4015个数据。这些数据表征了体育小镇在这11 年里连续的发展动态，可以用这些数据对整个系统的动力学模型中的参数进行辨识，以及对模型有效性的检验。

图2 基于B-样条函数插值的体育大数据产业系统连续动态

3.3 系统模型仿真

系统动力学模型是高度非线性的一阶常微分方程组（公式13～19），它是没有解析解的，即无法对整个模型进行积分得到关于的显性表达式，不能通过解析的方法去分析和观察系统的动态。因此，该研究只能通过计算机仿真的方法，获得模型高精度的数值解去解决问题。首先，必须把数学模型转化成计算机模型，该研究通过Matlab/Simulink 平台提供的模块化G 语言完成对整个系统动力学模型的构建（见图3）。

图3 体育大数据产业系统计算机仿真模型

3.4 模型的有效性检验

使用表2、表3 中的参数，便可以得到高精度的数值解，也就是模型的预测值，将它与实际调查值进行比较，根据二者之间的差异，确定系统原型与模型之间的行为相似性，模型的拟合效应显著性概率＜0.01（见图4）。

图4 模型的理论预测值与实际调查值

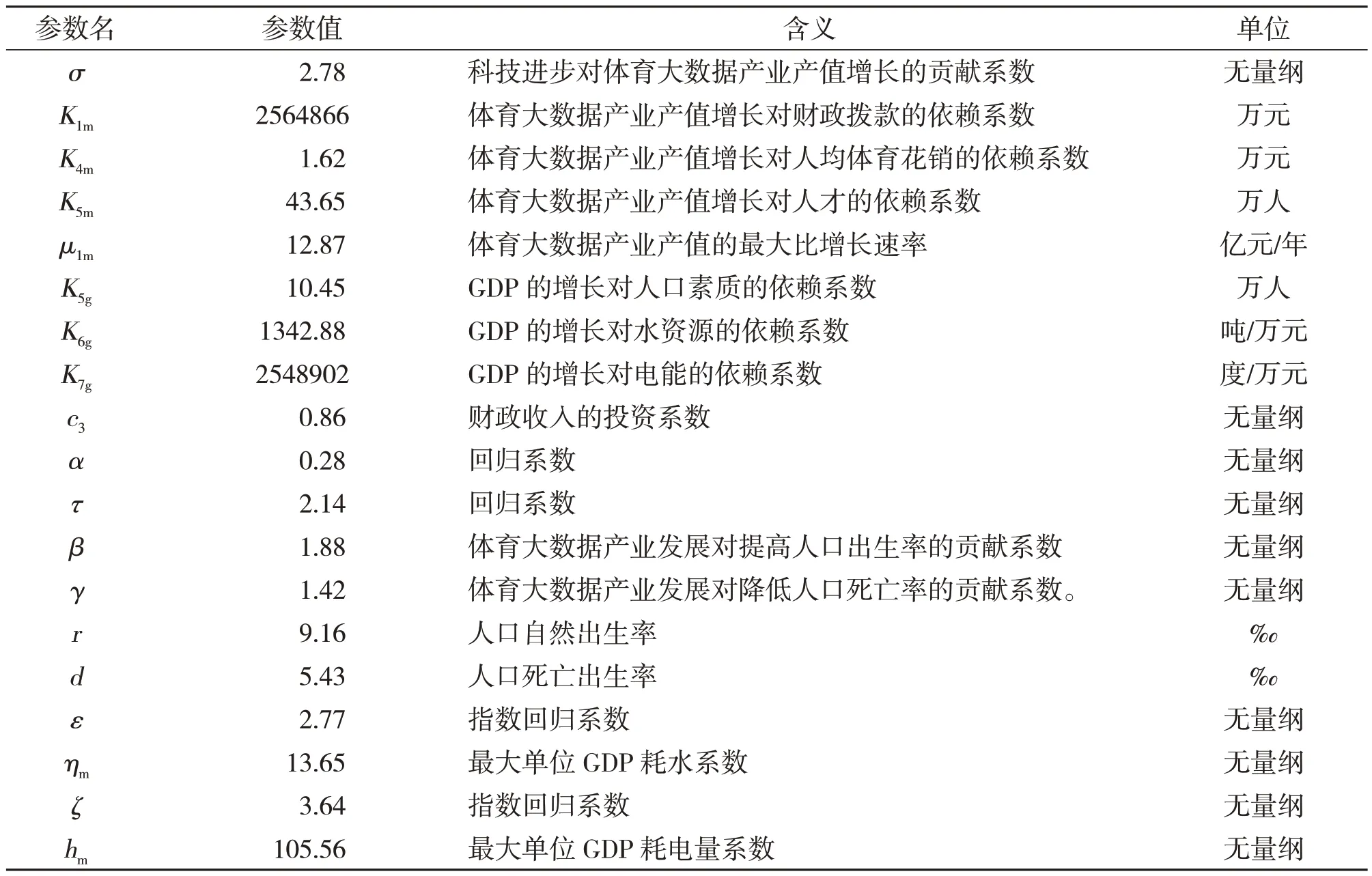
表3 模型中参数的最佳辨识结果

模型的拟合效应显著性概率，＜0.01，模型是有效的，它合理地选取了状态变量描述系统的动态，准确模拟了新兴体育小镇系统的内部结构，即各个子系统之间的相互关系和相互作用，以及由此产生的动力学机制。它可以作为计算机仿真实验的研究对象，完成新兴体育小镇体育大数据产业发展规划的研究。接下来，该研究在体育大数据产业有效模型的基础上，建立系统运行的模糊推理与评价系统，该系统兼顾区域经济、人口和环境的协调发展，评价体育大数据产业发展的现状及确定其增长的速率。在计算机仿真实验的基础上，确定新兴体育小镇体育大数据产业理想的发展动态，以及获得这样的发展动态需要采取的政策保障措施，即模型中可调节的政策参数优化。根据优化的政策参数可以有效地调节系统的动态，使系统朝着预期的方向发展。

4 模糊推理与评价系统

4.1 模糊集和模糊推理

建立模糊推理与评价系统，它主要有两种基本类型：Mamdani 型和Sugeno 型，该研究采用Mamdani 型在Matlab/Fuzzy Toolbox 平台上建立体育大数据产业发展模糊推理与评价系统，该系统最重要的构成是模糊推理规则，它相当于数学中的运算，如加、减、乘、除、乘方、开方、微分或积分等，它们能通过一些数生成另外一些数。模糊集和模糊推理相当于自然语言中的主语和谓语，通过如果（if）-那么（then）逻辑推理规则将它们组织起来，if 后面的部分称为前提（antecedent），then后面的部分称为结论（consequent），这也是人脑典型在布尔代数中逻辑运算主要包括逻辑与（AND）、逻辑或（OR）和逻辑非（NOT），“与-非”和“或-非”都可以实现任意复杂的逻辑推理命题，它们是逻辑推理的最小范式。因此，该研究主要采用“与-非”和“或-非”实现体育大数据产业发展模糊推理和评价。例如，如果财政收入隶属于“优”并且人均年收入隶属于“高”，并且人口净增长速率不是“优”，那么体育大数据产业产值的比增长速率隶属于“优”。这些都是人脑中的思维决策，把它表示成计算机能够识别的if-then 语句如下：

ifis“BEST”ANDis“HIGH”AND NOT/dt is“BEST”，thenis“BEST”。

表4 体育大数据产业系统评价的输入、输出指标模糊化

4.2 系统的动态过程优化

从图5 中可以看出，体育小镇在2018—2050 年经济增长、人口变化和资源环境保护方面是协调发展的，它们之间的相互作用，促使体育大数据产业快速健康地发展，同时后者的增长通过反馈作用直接或间接地促进了体育小镇的区域可持续发展。各个状态变量的变化曲线都不是规则的曲线，因为它们受到模糊推理与评价系统的调控，而模糊推理与评价系统并不是基于数学解析式建立的，而是由自然逻辑语言构建的，所以离散的体育大数据产业产值（）的比增长速率（）值，导致了系统动态曲线的不规则，但它恰恰能够反映系统真实的发展情况，而那些基于解析式的预测，往往都是比较规则的曲线，如指数、对数或幂函数曲线，理论预测特性较强，而真实的系统往往是不会有这样的发展变化动态的。

图5 体育小镇经济、人口和环境子系统各状态变量在2018—2050年的动态

4.3 系统的稳健性分析

体育大数据产业可持续发展系统的数学模型是非线性的，它具有若干个吸引子，也就是说系统由于不同初始值或受到扰动会稳定在不同的吸引子上。吸引子的位置与强弱主要取决于模型的形式，即系统的结构。该研究仿真实验结束时，系统稳定地平衡在状态空间中的一个工作点上，该工作点向量为：=［3451027.76，91768899.26，13891526.75，233326.83，231.52，3859.04，7493089.95］，它们分别是～在2050年前后达到平衡值。该研究利用Lyapunov间接法判断该平衡点的稳定性，即该吸引子的强弱。由于体育大数据产业系统是非线性系统，目前还无法直接通过数学解析的方法对它在某一平衡点上的稳定性进行研究，这时合理的方法是将非线性系统在平衡点处线性化，将成熟的经典线性系统分析理论与方法去判断该平衡点的稳定性。

体育大数据产业系统动力学模型（公式13～19）的模型表示为：/=（x，p），其中、、分别表示状态变量向量、状态方程向量和模型的参数向量。将非线性系统模型/=（x，p）在处对求偏导，得到：

这时在处原非线性系统/=（，）就可以转化为一个线性系统/=，矩阵为雅可比矩阵（Jacobian Matrix）或此线性系统的状态矩阵。根据Lyapunov 间接法，若/=在处是渐近稳定的，那么/=（，）在此处也是渐近稳定的。由于在x处式/=（，）与/=具有动态行为相似性，因此可以利用线性系统/=来研究实际非线性系统/=（，）在处的稳定性。

根据经典线性控制系统理论，系统的稳定平衡包括绝对和相对的稳定平衡。经计算，从图6 中可以看出/=线性系统的所有极点都位于s平面的左半部，且具有一对主共轭闭环极点，它们分别是-0.5+0.7143j 和-0.5-0.7143j，这对极点能够提供相对理想的阻尼比（0.57），并对体育大数据产业系统在处的动态起主导作用。

图6 体育大数据产业系统2050年运行平衡点的稳定性

上述分析表明，体育大数据产业在该研究所设计的系统动力学模型及政策参数的引导下，最终可以实现稳健的可持续发展。

5 结语

该研究以体育大数据产业为研究对象，在兼顾区域经济、社会、环境可持续发展的前提下，研究新兴体育小镇的体育大数据产业在未来的发展规划。在前期调查数据的基础上，综合运用系统动力学、模糊推理与评价系统和计算机仿真实验，对问题进行了深入定量的剖析和探讨。根据控制论的理论和方法，证明了在当前的系统参数下，体育大数据产业可持续发展系统是稳健的，它的相轨迹在2050 年能够稳健地运行在一个理想的工作点上，在此工作点上对系统线性化表征，在该点具有行为相似性的线性系统，具有一对理想的共轭极点，为政府部门提供了顶层设计依据，促进大数据政策的进一步落实与完善。