深水作业机器人推进器布局建模及推力分配
陈晓虎,尚伟燕,杨先海,易新华,代瑞恒,孙阳
(1.山东理工大学机械工程学院,山东淄博 255000;2.宁波工程学院机械工程学院,浙江宁波 315000)
0 前言
深水基础工程均在水面以下,其建造过程、后期维修均属隐蔽工程,施工难度极大[1]。研发能稳定行进于深水环境的潜水器,代替人完成复杂环境下的工程任务,具有重要意义。遥控无人潜水器(Remotely Operated Vehicle,ROV)是水下工作的重要工具,在军事侦察、搜索救援、水产养殖等多个领域广泛应用[2-3]。推进器布置及推力分配对潜水器的运动和作业能力影响巨大。为保持深水工程作业机器人各自由度运动合理,就必须解决ROV水平推进器推力分配问题,以最小化能耗或最小推力输出为优化目标将运动控制器产生的合力(矩)合理地分配到各推进器[4-6]。将ROV受到各个方向的力和力矩通过合理的推力分配方案使各推进器高效合理运行,可在降低能耗、减小误差、延长设备寿命等方面发挥重要作用[7]。
推力控制分配本质是一个在约束条件下的最优化问题。常见推力分配方法主要有:基于数学规划的优化方法、原始对偶法及其改进算法、伪逆法及其改进算法、序列二次规划等[8-10]。伪逆法求解迅速、结构简单,但输出推力易饱和使推进器持续高功率工作;原始对偶法的理论简单,有效解决推力饱和现象,但推力大小存在突变,降低了推进器使用寿命;序列二次规划算法可解决线性与非线性约束优化的问题,避免推力过饱和与推力突变,更适用于水平推进器的推力分配问题[11]。
ROV依靠4个水平推进器完成纵荡、横荡、艏摇的运动。研究ROV水平推进器对以上3个运动的影响,如图1所示建立ROV本体坐标系O-XYZ,坐标系原点O坐落在ROV的重心上,OX轴在ROV的纵荡方向上,OY轴在横荡方向上,OZ轴沿垂荡运动的方向。
ROV四个水平推进器的安装位置如图2所示。图中T1、T2、T3、T4分别为4个推进器产生的推力,其中推进器1安装在ROV船艏左侧,推进器2安装在ROV船艉左侧,推进器3安装在ROV船艉右侧,推进器4安装在ROV船艏右侧。4个水平推进器都安装沿OX方向与坐标系原点O相距D1、沿OY方向与坐标系原点相距D2的位置,安装角度均为θ。

图1 ROV本体坐标系
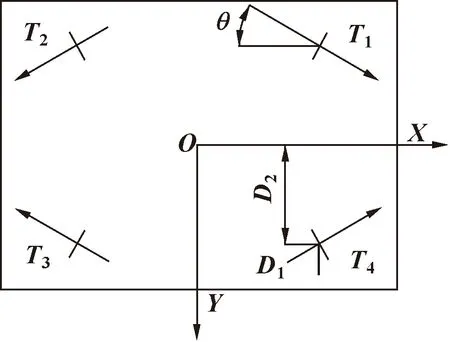
图2 ROV水平推进器布局
1 ROV水平推进器数学建模
根据图2所示的ROV水平推进器布局,可以得出各水平推进器的参数见表1。

表1 水平推进器参数
ROV运动过程中,在水平面内受到的外力可以分解为纵向阻力、横向阻力及偏航阻力矩,因此水平推进器所产生的合力需要能够应对3种外力的影响,其合力亦可分解为纵向力K、横向力M及偏航力矩N。因此每个推进器产生的推力可以如图3所示沿OX和OY进行分解。

图3 推进器推力分解
图3中:Tix=Ticosθ,Tiy=Tisinθ。推进器产生的纵向力与横向力分别为
K=T1x-T2x-T3x+T4x=T1cosθ-T2cosθ-
T3cosθ+T4cosθ
(1)
M=-T1y-T2y+T3y+T4y=T1sinθ+T2sinθ-
T3sinθ-T4sinθ
(2)
产生的偏航力矩为
N=T1xD2+T1yD1-(T2xD2+T2yD1)+T3xD2+T3yD1-(T4xD2+T4yD1)=T1(D2cosθ+D1sinθ)-T2(D2cosθ+D1sinθ)+T3(D2cosθ+D1sinθ)-T4(D2cosθ+D1sinθ)
(3)
进而求出ROV推进器的综合推力:
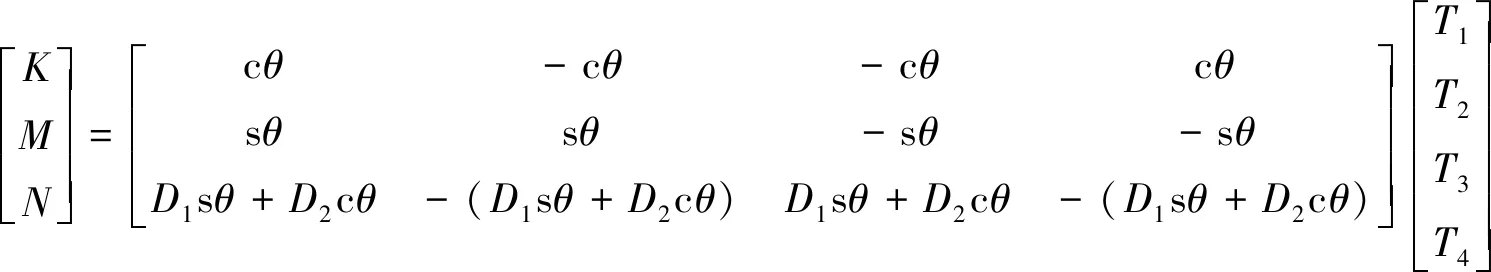
(4)
式中:cθ=cosθ,sθ=sinθ。
ROV推进器所产生的合力大小为

(5)
ROV推进器所产生的合力的方向为
(6)
φ的取值范围为[-π,π]。
所设计的水下工程机器人的工作环境中水流速度慢,通常低于2 m/s,所配置的水平推进器的最大推力为170 N,ROV尺寸为992 mm(L)×720 mm(W)×551 mm(H),正面迎水面积约为0.3 m2,通过ROV的形状阻力公式
f=0.5σAv2Cd
(7)
式中:f为ROV的形状阻力;σ等于海水密度除以重力加速度,其中海水密度1 035 kg/m3,重力加速度9.8 m/s2;A为特征面积即ROV正面迎水面积;v为ROV与水流相对速度;Cd为阻力系数,取0.9。
可得ROV与水流的相对速度为2 m/s时形状阻力约为57 N。为保证ROV在运动过程中拥有充足的前进动力,应使最大纵向力Kmax略大于最大横向力Mmax。已知单个推进器最大推力为170 N,推进器可通过正反转来改变推力方向,因此Kmax=680cosθ;Mmax=680sinθ,取最大纵向力Kmax与最大横向力Mmax差值为60 N可得
Kmax-Mmax=680(cosθ-sinθ)=60
(8)
求得θ=2π/9。
在安装角为2π/9的前提下,分析式(5)和式(6)发现4个水平推进器所产生的综合推力的大小和方向仅与每个推进器的输出推力及推进器的安装角度有关。将图2中各推进器推力的作用点平移至原点O,可知T1与T3共线,T2与T4共线。因此可以将式(1)和式(2)简化为
K=T1-3cosθ-T2-4cosθ
(9)
M=T1-3sinθ+T2-4sinθ
(10)
式中:T1-3为推进器1和推进器3的推力差,T2-4为推进器2和推进器4的推力差。对式(5)、式(6)进行求解可以得到以T1-3为横轴、T2-4为纵轴的关于综合推力大小和角度的图像,将二者进行叠加可以得到图4。
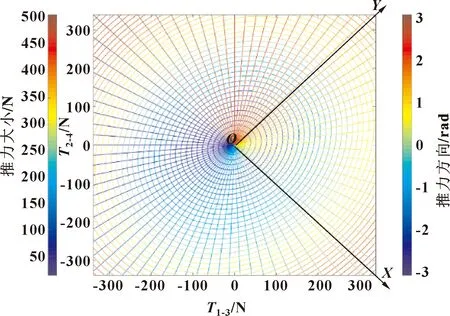
图4 综合推力大小与角度对照
图中的环形线条为推力大小的等高线,放射线条则为推力的方向。OX表示综合推力的方向为0,与本体坐标系的OX轴相同;OY表示综合推力的方向为π/2,与本体坐标系中的OY轴相同。分析图4不难发现:只要能够对水平推进器的推力进行合理分配,就可以实现在-π~π内得到任意大小的推力,能够充分应对在有效范围内的外力干扰。
2 水平推进器的推力分配
该ROV在水平方向共对称安装了4个推进器,4个推进器安装角均为40°,安装距离D1=400 mm、D2=300 mm。水下机器人在平面上3个自由度的运动受4个水平推进器的控制,针对某一特定的工作需求,都会存在多组推力分配方案。在此模型下利用两种方案对推进器进行推力分配仿真。
2.1 直接逻辑的推力分配
2.1.1 直接逻辑的推力分配方法
根据推进器的安装角度及安装距离的参数可得该推进器的推力方程为
(11)
根据上式可知各推进器的目标推力为
(12)
2.1.2 直接逻辑的推力分配方法仿真
为验证ROV的水平推进器的推力可以根据外部力的影响而自动调节,不妨将ROV所受的外力分解为纵向、横向、偏航三部分,对每一部分均以正余弦信号作为输入,使其不断生成随时间变化的力,各部分力的具体大小如下式所示
Ko=300sin(0.2t)
(13)
Mo=240cos(0.2t)
(14)
No=30sin(0.2t)
(15)
式中:Ko、Mo、No分别为ROV在纵向、横向以及偏航3个方向受到的力或力矩。
利用仿真软件对直接逻辑的推力分配进行仿真,观察在一个变化周期内ROV的实时输出功率及各推进器推力分配。通过仿真得到各推进器的推力如图5所示,ROV的实时输出功率如图6所示。
由图5可知:推进器1和推进器2输出的最大推力均达到了推进器的极限推力170 N,且在一个周期内有56%的时间在满功率运转;推进器3输出的最大推力也高达168 N;而推进器4输出的最大推力仅有101 N。直接逻辑的推力分配方法,存在着极大的分配不均现象,从而导致推进器叶片磨损不均,进而影响ROV的整体运动精度。分析图6可知:ROV四个水平推进器的实时综合功率最大值为2 337 W,最小值为1 590 W。

图5 直接逻辑推力分配结果 图6 直接逻辑综合输出功率
2.2 功率归一的推力分配
2.2.1 功率归一的推力分配方法
上述推进器推力分配方案会使其转速过高,持续高功率输出,严重影响电机的使用寿命。为了避免高消耗的分配方式,可以将4个推进器的输出推力转化为推进器的功率,将4个推进器的输出功率进行汇总,以实现用较低的功率满足使用要求,有效延长推进器的使用寿命。
探讨推进器功率与输出推力的关系,则需要知道推进器的推力和转矩。已知单个推进器的推力、转矩、转速、功率的关系为
Ti=KTρn2R4
(16)
Qi=KQρn2R5
(17)
Pi=2πRnQi
(18)
式中:Ti、Qi、Pi分别为单个推进器的推力、转矩和功率;ρ为工作环境的流体密度;n为推进器转速;R为推进器螺旋桨直径。
整理后可得功率与推力的关系式:
(19)
上式中n为变量,作进一步整理得功率的限定条件为
(20)
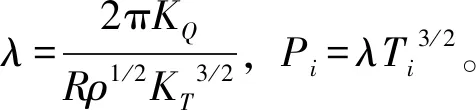
2.2.2 功率归一的推力分配方法仿真
将4个水平推进器的输出功率作为重要约束条件,目的是以最小的功率完成目标任务。利用仿真软件,基于SQP算法对ROV的4个水平推进器的推力进行仿真。按照式(13)(14)(15)的条件进行力的输入,式(20)作为求解目标函数,因λ为常数,所以λ的大小不影响最终推力分配的结果。最终推力分配仿真结果如图7所示,通过各推进器推力曲线可知,推进器1和推进器2推力最大值均为155 N,最大推力下降了8.82%,推进器3和推进器4的推力最大值均为120 N,4个推进器均未出现满速运转的情况。4个水平推进器的工作情况相近,磨损程度相当。
ROV的实时输出功率如图8所示,可得:ROV水平推进器的实时输出功率的最大值为1 940 W最小功率为1 580 W。
通过功率归一的推力分配仿真与直接逻辑的推力分配仿真结果的对比,可知在相同的输入条件下,进行功率归一以后的推进器1、2、 3的最大推力均明显降低,推力输出曲线更加平滑,推力突变现象得到有效解决。同时经功率归一后的推进器最大输出功率较未进行功率归一的推进器最大输出功率降低了17.1%,最小输出功率无明显变化。
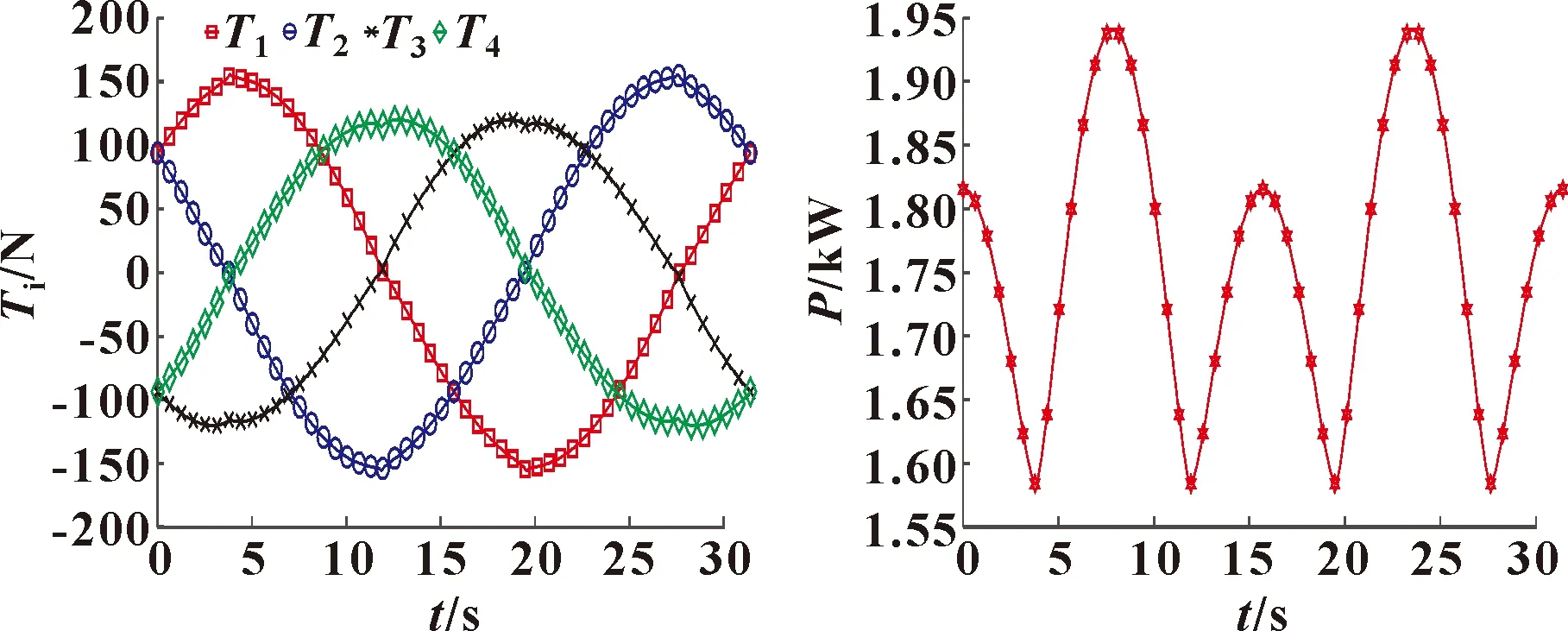
图7 功率归一推进器推力分配结果 图8 功率归一综合输出功率
期望推力与实际推力的关系如图9所示,图9中Fi为期望得到的ROV四个水平推进器输出力的合力,Fo为ROV四个水平推进器实际输出力的合力。通过Fo和Fi的对比曲线可以发现,二者的基本变化趋势一致且数值相当,证明了功率归一方案的可行性。
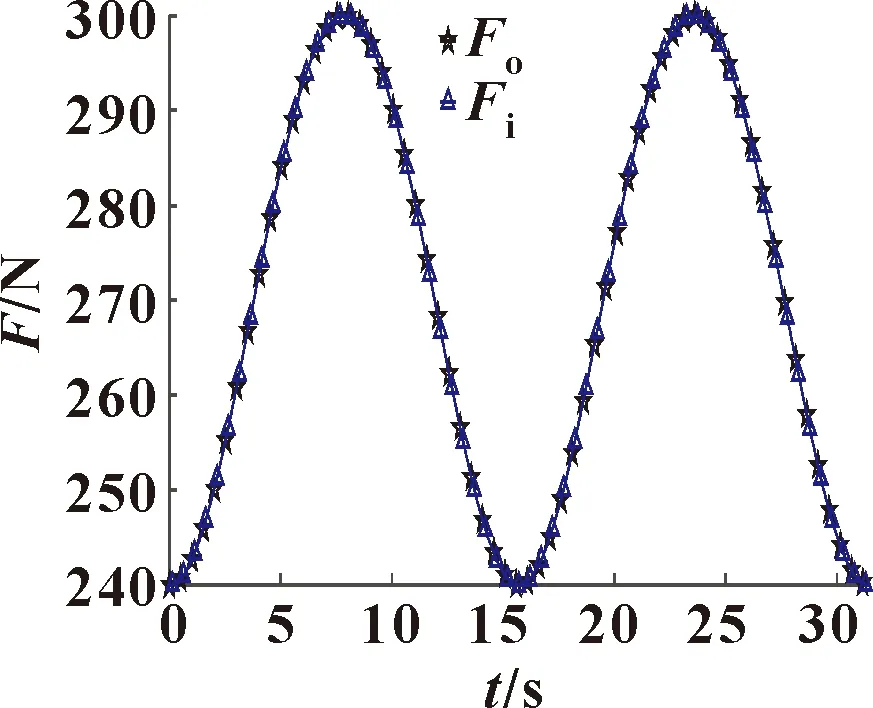
图9 期望输出力和实际输出力
3 结论
基于现有ROV的参数对其4个水平推进器进行了数学建模,分析目标推力与4个水平推进器之间的数学关系,并通过仿真软件进行了验证,最终得出以下结论:
(1)构建了ROV四个水平推进器的输出推力、安装角、安装位置与纵向力、横向力、偏航力矩之间的数学关系模型,确定了推进器的安装角为40°,并通过绘制综合推力大小与角度对照图证明了该方案的可行性,为进行功率归一的推力分配奠定基础。
(2)以4个水平推进器的综合输出功率最小作为目标函数,进行推力分配仿真,对功率归一和直接逻辑的推力分配方法仿真结果进行对比,功率归一方案的推进器最大输出功率有明显减小,最大输出功率减小17.1%。推进器1、2、3的最大推力也显著降低,其中推进器1的最大推力降低8.82%。无论是从能耗以及保护设备、延长使用寿命的角度看,功率归一的推力分配方法都比直接逻辑的推力分配方法有明显优势,更利于ROV在水下的安全作业。

