三轮全向移动机器人里程计在线校正方法研究

简傲，闵华松，黄文晖

(武汉科技大学机器人与智能系统研究院，湖北武汉 430081)

0 前言

移动机器人是当今机器人领域应用开发的热点。在移动机器人应用开发过程中，会遇到一个关键性的问题，即定位和控制问题，具体表现为移动机器人在全局坐标系下的位姿矫正问题。移动机器人在复杂多变环境中如何获得自身位置和姿态，以及通过怎样的方式到达目标位置是定位问题的关键。解决这样的问题常常需要用到多种类型的传感器进行信息融合，并设计适当的控制算法。移动机器人系统是一个非常复杂的系统，它需要融合对环境的感知能力、决策能力、自主规划能力以及控制与执行能力，具备相当高的智能性和自主性。

全向移动机器人是目前移动机器人中比较热门的课题，相比拥有常规轮子结构的移动机器人，它具备更优良的机动性，能够在狭窄空间内转弯以及向任何方向移动，这类机器人通常用于家庭、车间、医疗服务等。尽管全向移动机器人具有更好的机动性，但由于复杂的机械结构和特殊的轮子属性，使得全向移动机器人的控制变得极为复杂。全向移动机器人的位姿控制难度较大，所以市场上的全向移动机器人的精度普遍不高。对于如何提高全向移动机器人的定位精度，使它能够为后续的导航和精准作业提供保障，一直是各大高校和科研机构讨论和研究的热门课题。

移动机器人的定位精度必然受到两类误差的影响，即系统误差和非系统误差，且无法避免。系统误差是由控制模型和机械装配的不准确而产生的，例如机械器件的装配误差、车轮直径不相等、轮距的不确定性、控制参数的不确定性等；非系统误差则是由车轮打滑或者地面不平整等原因造成的。系统误差是移动机器人本身的属性，在长时间内几乎保持不变，而非系统误差可表示成车轮与地面之间关系的函数。因此，利用有效的传感器信息，对机器人的位置和姿态进行校准是有必要的。

在移动机器人经过规划导航到达目标点后，为使其在目标位置能够正常地进行工作任务，需要保证它在目标点的位姿精度能适应正常工作的要求。但是，目前的规划导航算法由于受系统误差和非系统误差的影响，会导致机器人在到达目标点的位姿偏差较大，需要经过校正算法来提高机器人到达目标点时的位姿精度，其中比较有效的方法是里程计校正法。

国内外关于移动机器人里程计校正方法的研究较多，较为经典的校正方法是1996年密歇根大学提出的针对两轮差速驱动机器人的里程计误差校正方法UMBmark。该方法指出了误差来源为轮子直径不等、轮子间距离存在不确定性，定量分析了系统误差的大小。文献[11]中将全向移动机器人的运动分为以下3种：纯旋转、直线运动、绕非零半径点旋转，使得机器人不仅能够跟踪所需方向也能跟踪既定的轨迹，在引入瞬时曲率中心的坐标和瞬时旋转半径后，建立更为精准的运动学模型，确定了机器人调速范围，设计出合适的模糊控制器。文献[12]中提出了通过机载惯性传感器来获取机器人姿态，用机器人姿态角的偏移来推导校正方程，不需要做近似计算。文献[13]中认为全向移动机器人的运动误差来源于运动学模型的不准确，即全向轮有内外圈，在机器人的运动过程中，内外圈交替地与地面接触，所以机器人中心到轮子的距离并不是一个固定值；为解决这一问题，对机器人的运动学模型进行改进，提高全向移动机器人的定位精度。文献[14]中提出了一种单目相机与增量型编码器相结合的视觉里程计，利用图像特征获取机器人的相对位姿并与编码器测得的机器人转向角结合，实现对车辆姿态和路标位置的实时估计。文献[15]中针对视觉里程计(VO)因累积误差导致机器人位姿估计存在偏差，设计了一种基于扩展卡尔曼滤波的位姿估计模型，利用惯性测量单元(IMU)结合重力加速度方向作为垂直方向参考，对视觉里程计航向、俯仰和侧倾3个方向姿态估计进行解耦，修正姿态估计的累积误差。文献[16]中针对里程计在定位过程中存在累积误差的问题，建立了一种通用的移动机器人里程计误差模型，通过处理激光雷达反馈数据对里程计误差进行实时反馈补偿。三轮全向移动机器人的动力学分析有助于提高里程精度，合理的动力分配和控制器设计能够大幅度提高机器人的里程计精度。文献[19]中利用牛顿欧拉法和简化的直流电机模型，在Simulink中建立一种简化的三轮全向移动机器人的动力学控制器，实现了存在摩擦情况下的速度闭环控制。

针对机器人里程误差的校正，比较成熟的方法是通过工程手段反复测量机器人的轨迹信息，然后根据里程误差为机器人的运动学模型添加校正系数，从而达到修正里程误差的目的。但是这种离线校正手段建立在地面平整且轮子与地面的摩擦始终不变的情况下，不具备鲁棒性和普适性，不同的工作环境需再次进行大量的实验，以得到校正系数，且无法应对地面环境的变化。针对离线校正方法的不足，本文作者采用扩展卡尔曼滤波算法与动力学分析相结合的方法，设计一种适用于三轮全向移动机器人在线里程计校正系统，通过仿真实验验证其有效性，并在实际平台上取得了预期实验效果。

1 三轮全向移动机器人建模

1.1 三轮全向移动机器人运动学

机器人的运动学特性是对机械系统工作原理的本质表述。而移动机器人运动学模型是机器人运动控制的基础，通过解析运动学方程，可以将机器人中心点的位移转化为每个全向轮上各自的转动，从而得到机器人的位姿、速度以及单个全向轮转速之间的关系，有利于分析和解决问题。文中的三轮全向轮底盘如图1所示。

图1 三轮全向轮底盘模型

图1中机身坐标系的原点与底盘几何中心重合，在机器人自身坐标系下，建立三轮全向移动机器人运动学方程。其中，、、分别表示3个全向轮的线速度，m/s；、、表示轮子的角速度，rad/s；为轮子中心到机器人中心的距离，m；为机器人整体的前向速度，m/s;为机器人整体的法向速度,m/s;为底盘的旋转角速度,rad/s。速度分解如公式(1)所示：

(1)

通过矩阵的逆变换可以求得机器人中心点的速度与全向轮线速度之间的关系，如公式(2)所示：

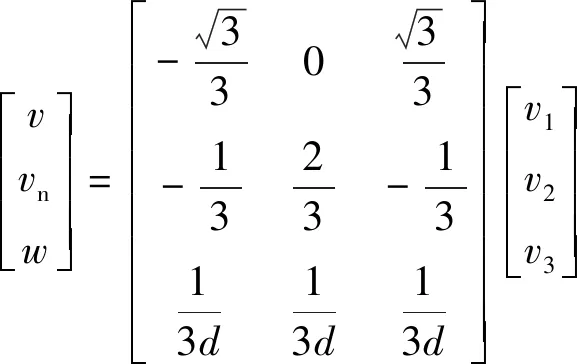
(2)

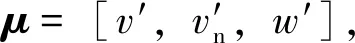
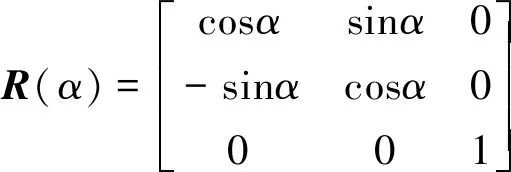
(3)

=()·

(4)

图2 三轮全向轮坐标变换

得到运动学方程后，可以由上位机发布机器人的速度指令=[′,′,′],然后根据运动学方程转换为全向轮附着电机所需要的PWM占空比，从而控制三轮全向移动机器人的运动。

1.2 三轮全向移动机器人动力学

运动学能够实现机器人整体速度和轮子速度之间的转换，通过运动学逆解,上位机能够及时发布控制指令使其运动到目标位置。然而，机器人受到自身和环境因素的影响，基于运动学的控制器并不能满足系统高精度定位的要求，所以需要对机器人的动力学进行建模。

机器人靠电机提供驱动力，全向机器人存在前向、法向的线加速度以及旋转的角加速度，由此可得三轮全向轮底盘的受力分析如公式(5)所示：

(5)

式中：为车体的质量，kg;为底盘整体的惯性力矩常数，kg·m；为底盘前向的滑动摩擦力，N；为底盘法向的滑动摩擦力，N；为底盘滑动摩擦力矩，N·m;为底盘前向的静摩擦力，N;n为底盘法向的静摩擦力，N；为底盘静摩擦力矩，N·m。

滑动摩擦力与机器人的速度成正比，所以有:

=·n=n·=·

式中：、n分别是、方向上的滑动摩擦系数，N·s/m；是关于的滑动摩擦系数，N·m·s/rad。

静摩擦力与接触面材质以及压力有关，可表示为

=·sign()n=n·sign()

=·sign()=·sign()

式中：、n分别是、方向上的静摩擦力，N；是关于的静摩擦力矩，N·m。

底盘整体受到的牵引力由电机提供，图1中已给出受力分析，进行矢量分解后如公式(6)所示:

(6)

轮子受到的牵引力以及牵引力矩如公式(7)所示：

(7)

为了更为便利地建模，需要对电机模型进行简化：

(8)

其中：为轮子半径，m;为减速比；为电机的转矩常数，N·m/A;为电机电流，A；为电机内部电阻，Ω。由此可以得到电机驱动力(N)与电压(V)以及转速(m/s)之间的表达式如公式(9)所示:

(9)

联立公式(5)—(9),可以用状态空间的形式来表示三轮全向轮底盘的动力学模型，如公式(10)所示。其中，()=[,,]、()=[,,]，为。

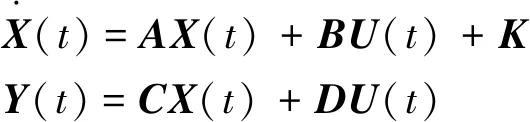
(10)

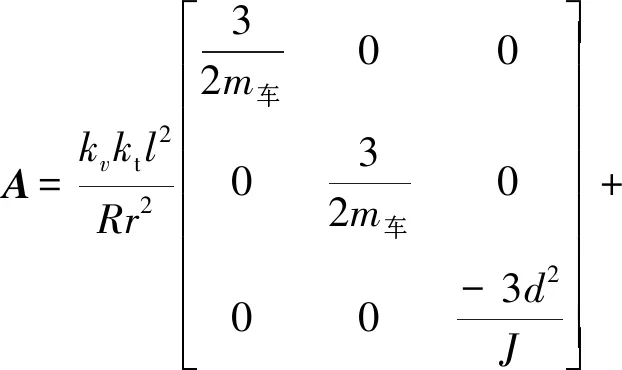
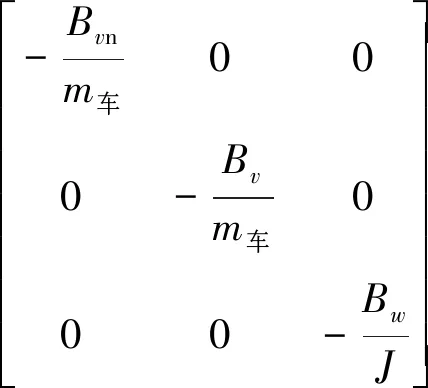
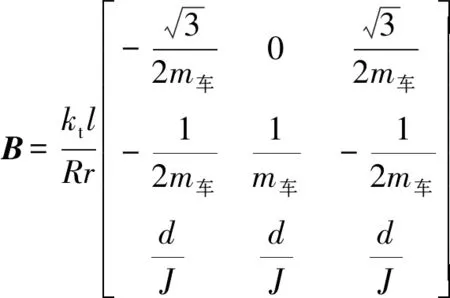
有了三轮全向轮底盘的动力学模型,可以更为精确地控制机器人。全向轮与地面的摩擦因数低，机器人自身惯量大，运动过程中容易发生偏移，且偏移误差会不断累积，如果将加速度控制在一定的范围内，能有效减小控制难度。

2 在线里程计校正方法

2.1 卡尔曼滤波算法

传感器精度大多会受到自身刷新频率和环境因素的影响，导致测量结果发生漂移，且误差会随着时间的推移累积，所以精确的测量需要利用合适的滤波器对数据进行处理。卡尔曼滤波(Kalman Filter,KF)的核心思想是将测量更新与预测更新结合起来，得到最佳的状态估计值。扩展卡尔曼滤波(Extended Kalman Filter ,EKF)和KF不同，EKF能够处理非线性系统。两者都需要建立系统的状态方程和观测方程，如公式(11)所示：

(11)

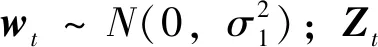
将KF的状态估计分为两个步骤，即状态预测和状态更新。其中，状态预测主要是针对状态向量和系统误差，如公式(12)所示：

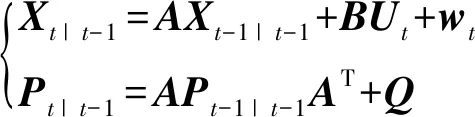
(12)

式中：为系统状态量对应的协方差；为系统过程的协方差矩阵。而状态更新主要分为以下3个方面。

更新KF增益：

=|-1(+)

其中：为观测噪声的协方差矩阵。

由测量值更新系统状态估计：

|-1=-1|-1+(--1|-1)

更新误差协方差：

|-1=(1-)-1|-1

2.2 基于EKF的里程计融合

使用KF来进行传感器融合是一种比较常用的手段，其观测方程有多个，即有多个传感器，由不同传感器的测量值来估计系统的状态向量。其观测方程可表示成公式(13)的形式。

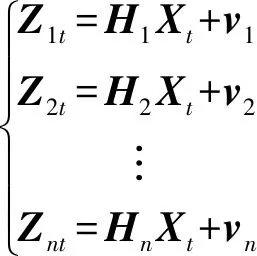
(13)

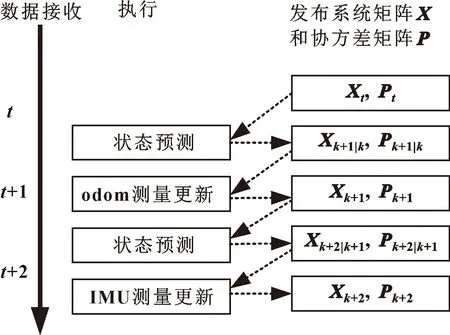
图3 三轮全向移动机器人状态更新

文中通过扩展卡尔曼滤波算法将编码器和IMU的数据进行融合，得到三轮全向移动机器人的里程信息，如图4所示，以便设计合适的控制算法来校正机器人的里程误差。

图4 获取机器人位姿信息

选取适当的变量作为EKF的系统状态，三轮全向移动机器人运动在二维平面上，选择=[,,,,,]作为系统变量。如图5所示，、表示机器人在平面上的坐标，表示平面上相对于初始位姿的角度,、表示平面上沿、方向的速度，表示机器人自身的旋转角速度。

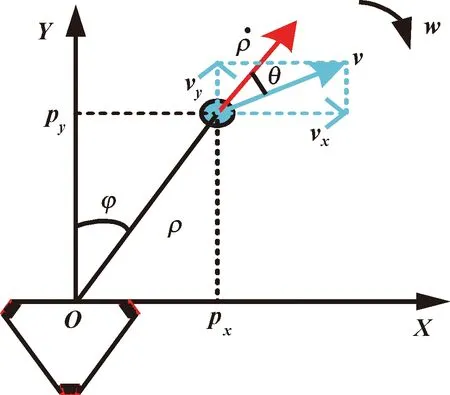
图5 机器人运动状态

单独用编码器充当移动机器人的里程计来反馈机器人的位姿效果不够好，因为机器人的系统误差和非系统误差在实际运动过程中无法避免，打滑等情况会造成编码器推算的姿态误差累积，而加入IMU和编码器的信息融合后测量得到的姿态信息能有效减少误差。

(14)

(15)

=，表示系统状态的不确定度的协方差矩阵。里程计提供的位置信息的准确度高于速度信息，所以>>。编码器的测量误差需要传感器厂家提供。

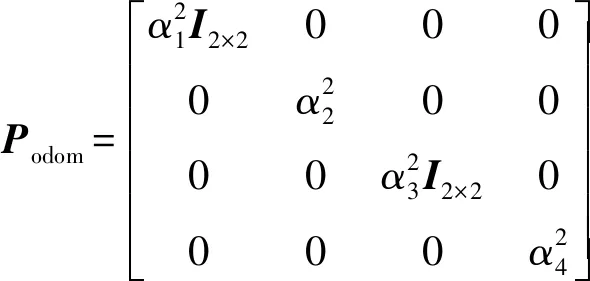
(16)

()=[,,]=

(17)

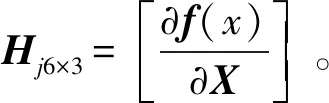
IMU的EKF状态更新的主要方程如下：

2.3 校正方法

本文作者通过EKF与三轮全向移动机器人动力学结合的方法来校正机器人的里程误差。首先是获取机器人在运动过程中在全局坐标系下的位姿和姿态，这里只需要通过EKF对编码器和IMU数据作处理就可以得到位姿信息以及速度信息，将位置和速度信息与参考值作比较，设计位姿控制器和速度控制器。文中为PID控制器，根据误差值并结合前面的受力分析，对机器人作新的动力分配，减小误差值。算法原理如图7所示。

图6 三轮全向移动机器人里程误差

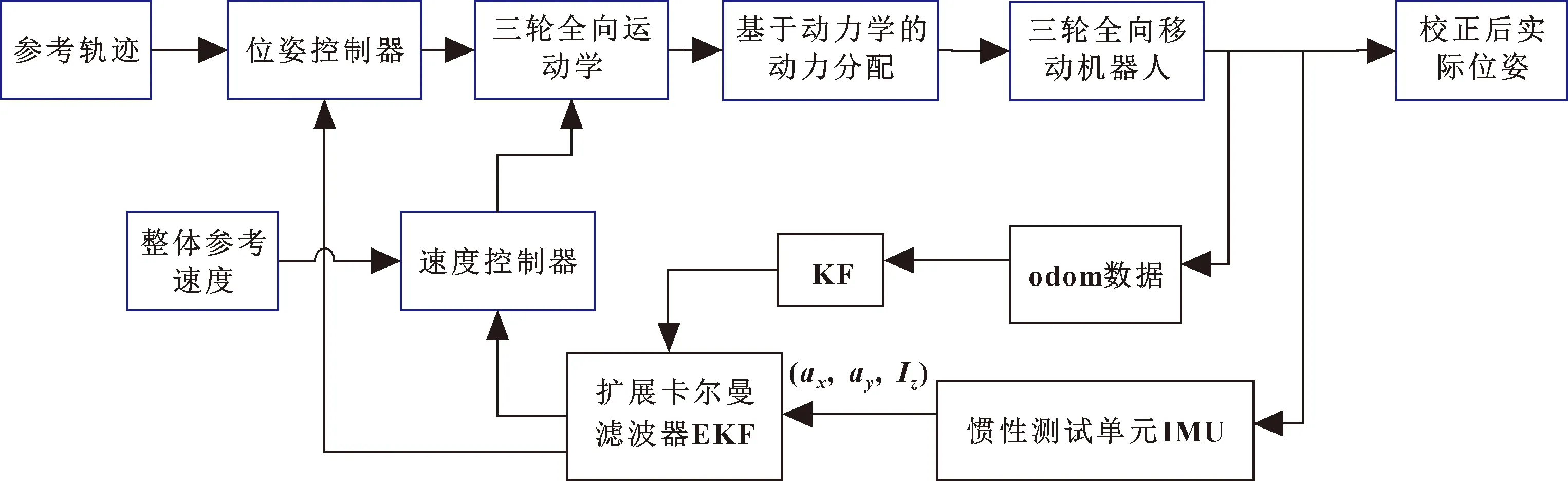
图7 校正算法原理

3 实验结果与分析

3.1 三轮全向移动机器人V-REP仿真

三轮全向轮底盘的特殊机械结构，使它在平面内拥有3个自由度，机器人可以在不改变自身姿态的情况下朝平面任意方向运动。导入移动底盘模型后，可以在V-REP中构造全向轮的仿真模型，并添加约束。

全向轮的运动学本质上是在靠轮毂外围安装一周与轮毂轴线呈一定角度的无动力辊子作为轮胎，该辊子不仅可绕轮毂轴公转，也能在地面摩擦力作用下绕各自的支撑芯轴自转。两种运动的合成使得接触地面的辊子中心合速度与轮毂轴有一定的夹角，通过调节轮毂速度可改变辊子中心合速度的大小和方向。

在V-REP中，复杂的机械结构会使得仿真不够流畅，控制难度增大，所以对全向轮模型进行简化。由于全向轮与底盘的接触是一个点，这个点既可以平动也可以滑动，所以将全向轮简化成两个材料不同的球体和2个电机关节。电机互成90°，一个使能作为驱动轮，一个不使能作为滑动轮，如图8所示。

图8 全向轮简化模型

在V-REP中搭建的三轮全向轮底盘仿真模型，与实物的属性保持一致。仿真下能直观地模拟三轮全向移动机器人的运动过程，在模型中添加多种传感器信息，能够及时地反馈机器人的里程信息，分析算法的有效性，如图9所示。

图9 三轮全向移动机器人V-REP仿真

3.2 对比实验及评价指标

本文作者利用V-REP与ROS进行联合仿真，能够利用上一章节提出的算法计算机器人自身在全局坐标系下的位姿，并结合动力学作动力分配，以及时地修正里程误差，最后在ROS中发布校正后的机器人坐标。

移动机器人的运动可以分为直线运动和弧线运动，所以移动机器人的里程误差校正，一般是让机器人作正方形轨迹和圆弧轨迹运动。与传统的差速机器人不同，三轮全向移动机器人在平面内具有3个自由度，进行正方形轨迹运动的时候，在转角处可以在不改变自身姿态的情况下作横向直线运动。

为验证算法的优越性和有效性，仿真中在机器人的前进路径上设置微小的不平物。

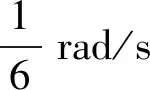
本文作者提出的在线校正方法基本不受地面环境的影响。文献[20]中的离线校正方法会严重偏离期望轨迹，由于无法很好地感知机器人自身位姿信息，不能及时调整自身姿态，以对轨迹作校正。为判定算法，设计评价指标，进行仿真实验，结果如图11所示。仿真结果证实了该方法的鲁棒性和普适性。

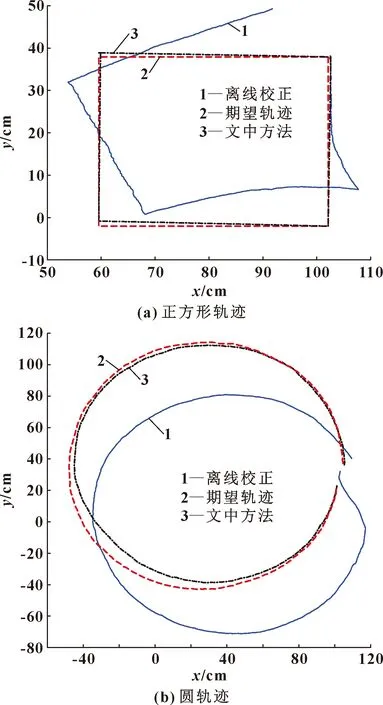
图10 对比实验效果

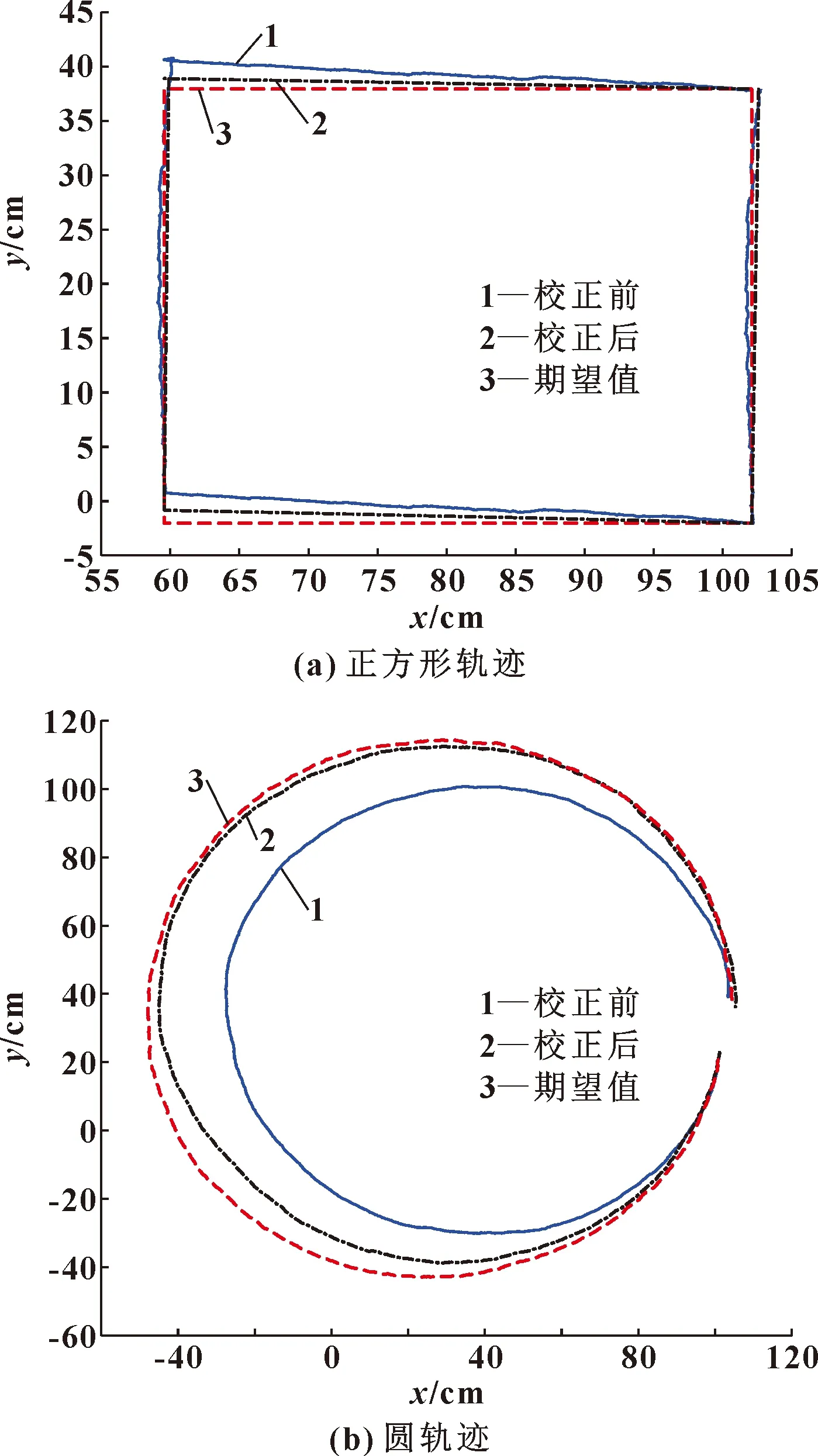
图11 仿真实验效果

正方形轨迹可以反映机器人直线运动过程中横向和纵向的误差校正效果，圆弧轨迹能反映机器人姿态误差校正效果。仿真中，机器人作正方形运动，横向和纵向的误差都归类为径向误差，误差改善率为。径向误差的定义如公式(18)所示：

(18)

式中：为实验次数。可通过比较误差改善率来判断校正方法的有效性，其定义如公式(19)所示：

(19)

其中：和分别表示校正前和校正后径向误差的平均值。

机器人沿着圆形轨迹运动，为得到姿态误差的改善效果，可以用期望圆弧半径、校正前的平均圆弧半径和校正后的平均圆弧半径，来评价姿态误差改善率。则可以表示为

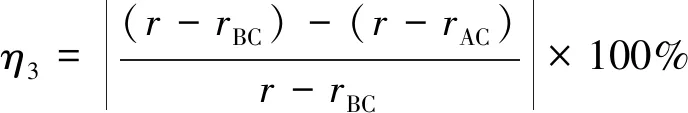
(20)

从仿真结果看，机器人的位置误差和姿态误差均得到了改善，采集仿真数据求取平均值可得为68.14%、为72.33%，验证了算法的有效性。

3.3 实际平台效果

以实验室搭建的实物机器人为基础，搭建了模型并进行实验。实物部分参数如表1所示。

表1 全向移动机器人部分参数

全向轮底盘的3个电机互成120°进行安装，将全向轮底盘分为3个关键模块：电源转换模块、驱动模块、控制模块。电源转换模块实现电压的转换，驱动模块控制电机的运作，控制模块发布运动指令和传感器信息采集，实物如图12所示。

实物实验分为径向误差改善实验以及弧度误差改善实验。径向误差实验步骤如下：

步骤(1)，如图6所示，设置控制程序，使机器人从原点运动到，机器人运动速度为0.2 m/s、运动距离为40 cm；

步骤(2)，机器人停止移动后，测量机器人相对于参考坐标系的绝对位置并记录；

步骤(3)，重复10次步骤(1)、(2)，根据公式(18)，求出校正前的径向平均误差;

步骤(4)，在程序中引入文中所提的在线校正方法，调试控制器参数，重复10次步骤(1)和步骤(2)，求出校正后的径向平均误差;

步骤(5)，根据公式(19)计算误差改善率。

整合测量结果可得，校正前的径向平均误差为2.41 cm、校正后的径向平均误差为0.82 cm、径向误差改善率为65.98%。

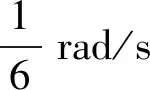
图12 三轮全向移动机器人实物

4 结论

本文作者提出了一种减少移动机器人里程误差的在线校正方法。相比于传统的离线校正方法，该方法能够及时地计算机器人的位姿，并根据位姿信息和速度信息及时校正机器人的里程误差，能够适应地面环境多变的情况，具有普适性和鲁棒性。在仿真和实际平台上的实验效果证明了所提校正方法的有效性。

文中算法可以有效解决机器人自身定位精度问题。除了自身定位外，还需要对外部环境进行感知，使机器人获得更强大的功能和更高精度的定位效果。因此，后期的工作考虑为机器人添加3D相机和激光雷达等传感器，扩展其外部感知能力，使它能够适应更多变的工作环境和更复杂的任务需求。