阻尼结构长扭叶片接触刚度与振动频率研究*

隋永枫,郑飞逸,蓝吉兵,傅建中,魏佳明

(1.浙江大学 工程师学院,浙江 杭州 310027;2.浙江大学 机械工程学院,浙江 杭州 310027;3.杭州汽轮机股份有限公司,浙江 杭州 310022)

0 引 言

长扭叶片是工业汽轮机的核心零部件。长扭叶片的效率、强度和振动频率是制约工业汽轮机发展的主要因素[1,2]。随着工业汽轮机的大型化发展,长扭叶片的尺寸越来越长,而叶片的刚性却随之下降,由此产生的振动问题,必须引起十分的重视。

摩擦阻尼是一种结构简单、减振效果好、制造成本低的阻尼结构,目前已经被广泛应用在大型发电汽轮机的长扭叶片上[3,4]。与大型发电汽轮机相比,工业汽轮机运行转速更高、工况复杂多样,因此,在工业汽轮机长扭叶片设计中,引入摩擦阻尼结构,是保障叶片安全运行的有效方法[5-7]。

在阻尼结构长扭叶片设计过程中,需要获得叶片准确的振动频率,但是摩擦接触面使得叶片成为一个非线性的、刚度和阻尼随时间变化的振动系统,导致对叶片的振动频率求解比较困难。其中,接触刚度直接影响了接触面之间的摩擦力以及接触状态的转换条件,从而影响了叶片振动频率的准确性。

PETROV E P等人[8,9]在研究阻尼结构叶片振动特性时,考虑了以试验或经验得到的切向刚度和法向刚度,将非线性方程组等效为线性方程组进行求解。徐自力等人[10]建立了阻尼结构叶片摩擦力的本构关系,较好地描述了接触面的接触、粘滞、滑移状态。谢永慧等人[11,12]对火电、核电汽轮机末级大型长扭叶片进行了优化研究,建立了叶片材料摩擦动力特性试验台,获得了接触刚度与材料迟滞曲线的关系。谢方涛[13]研究了叶片围带安装角对振动频率的影响,研究发现,叶片频率随着围带安装角的增加而增加,并且安装角的增大削弱了围带的减振效果。王威涛等人[14]根据哈密尔顿原理,研究了叶片的振动频率,研究发现,接触面间隙对叶片共振频率的影响很小,而叶片幅值随着接触面间隙的增大而增大。

综上所述,学者们在进行摩擦阻尼结构振动分析时,通常采用的方法有时域分析法和频域分析法等。时域分析法求解精度高,但其过程复杂,耗时很长。而频域分析法通过傅里叶变换,只保留周期变化位移、摩擦力的一次项,因此,其具有求解速度快的优点;但是对于高阶谐波影响显著的振动问题,采用频域分析法求解时误差较大。

时域频域交互法综合了以上两种方法的优点,又克服了其中的缺点,即通过快速傅里叶变换(fast Fourier transform,FFT)大幅度提高了非线性振动问题的求解速度。但是用该方法时需要考虑频率的泄漏和混叠问题,同时还需要经过多次迭代计算,因此,其求解过程相对比较复杂。

以上的研究主要集中在理论和实验两个方面,目前用于计算叶片接触刚度的方法在公开文献还少有提及。

因此,笔者在赫兹接触理论与G-W(Greenwood-Williamson)模型基础上,提出一种带刚度修正系数的接触刚度计算方法,用于叶片频率分析。

首先,笔者进行叶片频率试验,以获得叶片共振频率的试验值;然后,使用Matrix27单元模拟接触刚度,进行叶片频率有限元分析,确定刚度修正系数;最后,将围带减薄后再次进行叶片频率的分析和试验。

1 长扭叶片接触刚度分析

1.1 接触刚度计算公式

根据赫兹接触理论和G-W模型,接触面的粗糙程度是随机的,其表面波峰的高度是互相独立的,表面波峰可以简化为微小的球形体,且波峰的高度服从高斯分布。

综合文献[15，16]的研究结果，经推导可以得到接触面法向力F、法向接触刚度kn之间的关系式为：

(1)

式中：λ—表面的粗糙度；x—微观接触长度变量；x0—仅与表面粗糙度有关的几何特征参数。

在此，笔者定义刚度修正系数η为：

(2)

因此有：

(3)

同时，利用MINDLIN R D[17]的研究结论，法向刚度kn与切向刚度kt的关系式为：

(4)

式中：ν—材料泊松比。

1.2 接触刚度参数分析

由式(3)可知:影响法向接触刚度kn的主要参数为接触面法向力F、表面粗糙度λ和刚度修正系数η。接下来笔者分别对此进行分析:

(1)粗糙度对接触刚度的影响分析。根据加工工艺,叶片摩擦阻尼接触面的粗糙度λ一般为3.2 μm或6.3 μm,即λ通常是确定的数值,它的变化范围很小,因此,可将粗糙度λ当成常量处理;

(2)接触面法向力F对接触刚度的影响分析。文献[18]基于G-W模型,考虑材料的弹塑性变形,研究了材料为耐热不锈钢的燃气轮机轮盘结合面接触刚度的变化规律。该文献研究表明:kn随着接触应力Pn的增大先增大后减小;当Pn较小时,表面参与接触的球形体较少,kn表现出较强的线性行为;当Pn大于某一数值时,接触的球形体数目增加使得变形量减缓;当Pn接近材料的屈服极限时,接触的球形体发生塑性变形,变形量快速增大,kn值快速变小。

研究表明,当Pn小于材料的屈服极限时,kn与Pn基本上为线性关系,此时Pn满足Pn≤300 MPa。笔者研究的长扭叶片的材料为耐热不锈钢,与燃气轮机轮盘的材料类似,两者的力学性能比较接近,只是在化学成分、物理参数上略有不同。因此,笔者使用式(3)计算接触刚度时,Pn应该满足Pn≤300 MPa;

(3)刚度修正系数η对接触刚度的影响分析。由式(2)可知:刚度修正系数η与接触面的表面粗糙特性有关,对于已知材料和加工方式的接触面,其η是定值。由于叶片的振动频率由质量、刚度矩阵决定,当叶片结构不变时,改变叶片的接触刚度,可以得到叶片不同的振动频率fe。根据这个原则,首先，笔者通过试验获得叶片固有频率值,然后，给接触刚度修正系数η赋予一个初始值,通过式(3,4)计算接触刚度,不断调整η的数值,得到不同的接触刚度,最后，通过数值分析,得到叶片不同的频率fi,当fi与fe的误差小于5%时,认为η满足要求。

因此,进行叶片频率试验,获得叶片固有频率值fe,是确定触刚度修正系数η的关键步骤。

2 长扭叶片共振频率试验

2.1 试验概述

叶片振动频率试验场地为杭州汽轮机股份有限公司32T动平衡车间,场地的硬件设施、测试流程符合美国石油学会API612标准。

笔者分析的叶片为新开发的某型末级扭叶片,叶根为斜齿枞树型结构,叶片采用中间凸台接触面和围带接触面的摩擦阻尼结构。

叶片的外形图如图1所示。

图1 叶片外形结构图

图1中,叶片材料为沉淀硬化型不锈钢,转子材料为铬钼镍钒合金钢。

试验前,笔者取整圈叶片的任意3个叶片为试验点,将应变片和压电片贴在叶片的叶型部分上;应变片与采集模块连接采用半桥联接,即1片工作片和1片补偿片;为保障试验信号不受外界干扰,使用较粗的屏蔽线对应变片和压电片进行封装,屏蔽线按照S形弯好,再使用胶水将其固定在叶片上,最后在屏蔽线表面上覆盖厚度为0.1 mm的不锈钢薄片,并点焊牢固。

叶片压电片的安装如图2所示。

图2 压电片的安装

笔者使用高速动平衡机进行整圈叶片的振动频率试验。

安装有整圈叶片(末级)的试验转子如图3所示。

图3 动平衡机仓内的试验转子

笔者在动平衡机舱内安装3根喷管,喷管的内径分别为8 mm、10 mm、12 mm。喷管出口与叶片的距离为10 mm,压缩空气从喷管喷出对叶片进行激振。

激振喷管如图4所示。

图4 激振喷管

笔者在试验转子上安装采集模块,用于收集应变片和压电片产生的振动信号,并通过模块上的无线路由器,将信号传送至计算机实时显示、存贮和处理。

信号采集模块如图5所示。

图5 叶片振动数据采集模块

2.2 试验结果

因为叶片的额定工作转速为5 000 r/min,因此试验从转速5 00 r/min开始记录,然后升速至5 300 r/min,再降速至1 000 r/min中止记录,在整个升速、降速过程中,都使用压力为0.4 MPa的压缩空气对叶片进行激振。

通过多次试验,测得叶片4节径1阶共振转速为5 210 r/min,5节径1阶共振转速为3 808 r/min,6节径1阶共振转速为3 070 r/min,为下一步确定刚度修正系数提供了条件。

叶片4节径1阶的共振转速测试结果如图6所示。

图6 叶片4节径1阶共振转速/(r·min-1)

叶片5节径1阶的共振转速测试结果如图7所示。

图7 叶片5节径1阶共振转速/(r·min-1)

叶片6节径1阶的共振转速测试结果如图8所示。

图8 叶片6节径1阶共振转速/(r·min-1)

3 长扭叶片静态结构分析

笔者先使用有限元软件ANSYS进行叶片的静态结构分析,完成静态结构分析后,通过ANSYS后处理功能,读出接触面节点的接触应力和面积,利用接触应力乘以面积,得到单个节点的法向压力,将其汇总后得到接触面的总法向压力。

由于叶片-转子系统具有循环对称特性,笔者取单个叶片对应的扇区进行分析,其有限元网格如图9所示。

在叶片-转子循环对称模型中,笔者将扇区的侧向面C1、侧向面C2定义为循环对称约束,M1为中间凸台接触面,M2为围带接触面。

模型的循环对称面、接触面编号如图10所示。

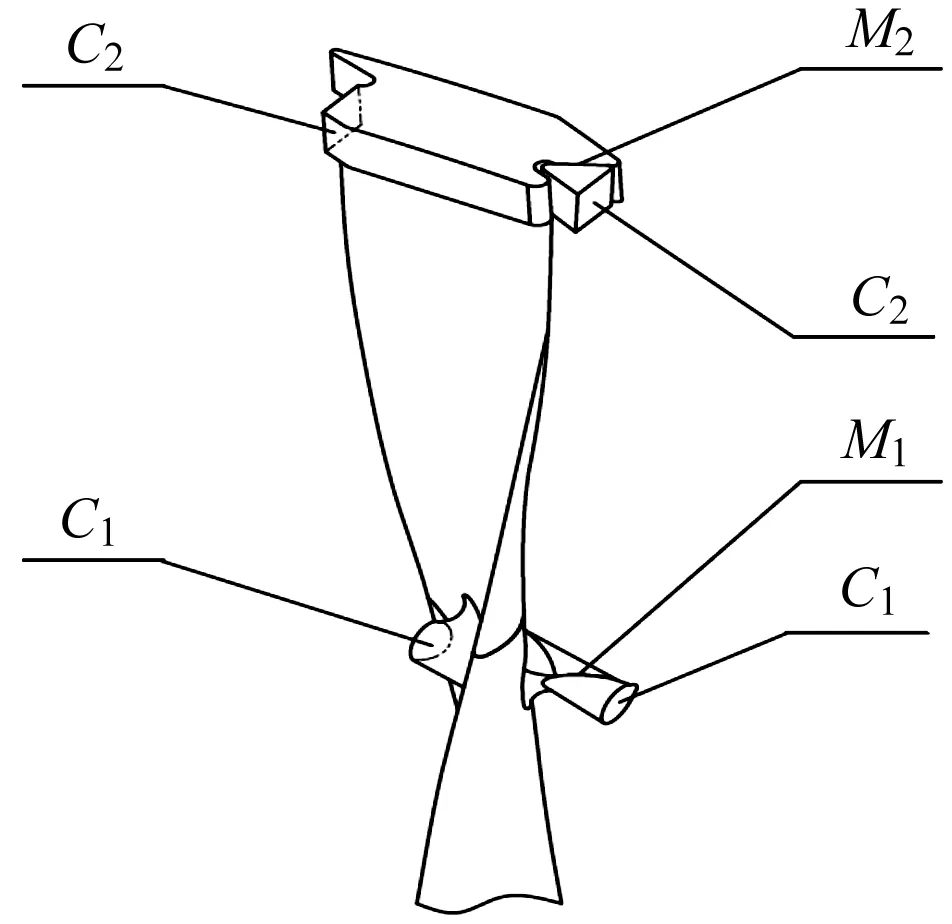
图10 叶片的循环对称面和接触面

为了确定其刚度修正系数,笔者首先分析了5节径1阶共振转速3 808 r/min时叶片的应力情况,以及中间接触面M1的接触应力、围带接触面M2的接触应力。

笔者利用ANSYS软件的后处理功能,获取接触面的单元接触应力和单元面积,将单个单元的接触应力和面积相乘,得到单元的法向压力,然后将其汇总得到接触面的总法向压力,如表1所示。

表1 接触面法向压力

4 长扭叶片振动频率分析

4.1 接触面线性化处理

笔者把叶片对应的两个接触面离散为多个节点,在对应的两个节点之间建立Matrix27单元,以模拟接触面的接触刚度。围带面M2接触面的Matrix27单元如图11所示,中间面M1的Matrix27单元图略。

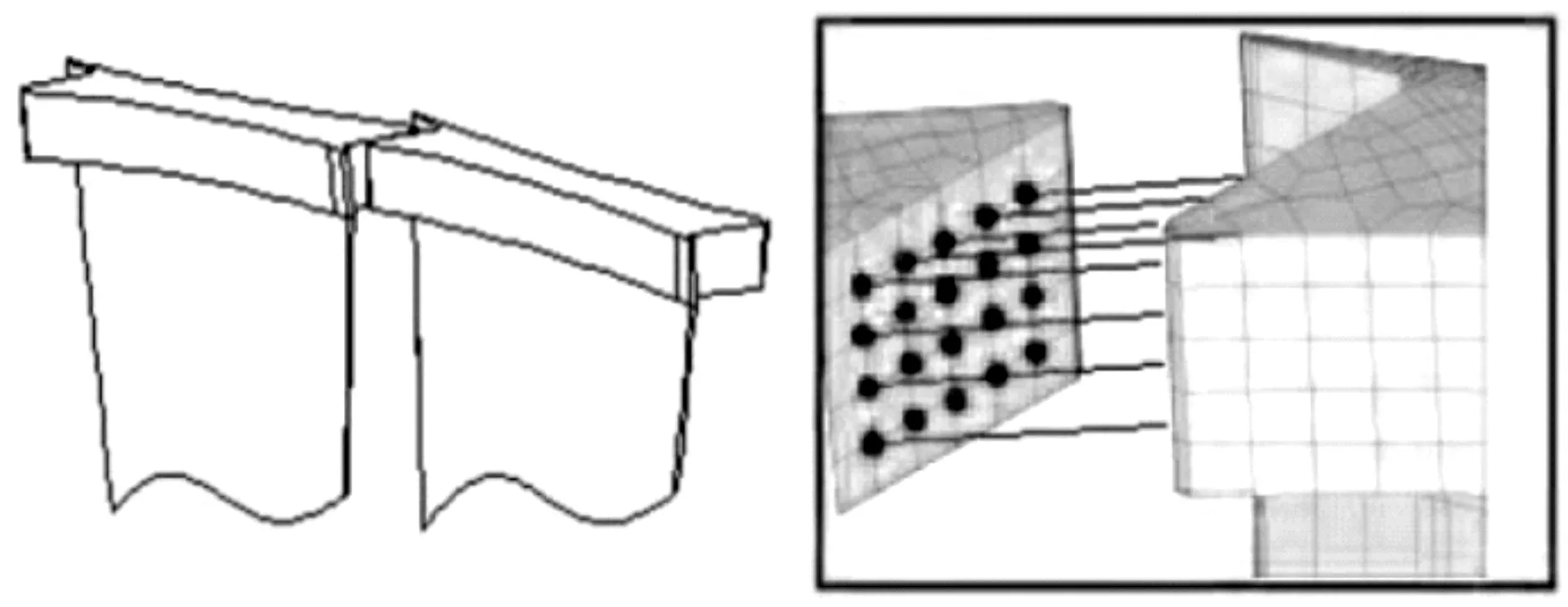
图11 围带接触面多点Matrix27单元示意图

中间面M1的Matrix27单元数量为37个,围带面M2的Matrix27单元数量为33个。为了提高分析效率,笔者假设同一接触面上的每个Matrix27单元的接触刚度均相等。

4.2 刚度修正系数计算

通过试验,笔者获得叶片5节径1阶共振转速为3 808 r/min,对应的固有共振频率为fe=317.3 Hz;通过调整刚度修正系数η,获得不同的接触刚度,然后进行叶片振动频率分析,获得共振频率的计算值fi。

fi与η的关系曲线如图12所示。

图12 共振频率fi与刚度修正系数η的曲线

由图12可知:当η=10时,计算得到的叶片共振频率为303.1 Hz,与fe的误差最小,误差为4.58%。因此,笔者取刚度修正系数为η=10。

4.3 整圈叶片节径振动分析

长扭叶片的额定工作转速为5 000 r/min,为了掌握不同转速时叶片频率的变化规律,笔者分别计算以下6种转速3 000 r/min、3 500 r/min、4 000 r/min、4 500 r/min、5 000 r/min、5 500 r/min时叶片的振动频率。

在进行频率分析之前,笔者先进行叶片静态结构分析,获得以上6种转速时接触面的法向压力F,然后取刚度修正系数η=10,计算其接触刚度。

叶片接触面的法向刚度kn如表2所示。

表2 中间面M1接触刚度

叶片接触面的切向刚度kd如表3所示。

表3 围带面M2接触刚度

根据表(2,3)的接触刚度,笔者进行叶片频率分析,得到6种转速时叶片的1阶节径振动频率数据,如表4所示。

表4 叶片1阶节径振动频率/Hz

笔者根据表4的数据绘制叶片节径振动坎贝尔图,如图13所示。

图13 叶片1阶节径振动坎贝尔图

由图13可知:节径数为m的频率曲线与k=m的倍频线交点对应的转速,为叶片的m节径共振转速。

叶片共振转速计算值与试验值的对比结果,如表5所示。

表5 叶片1阶共振转速对比

表5中,叶片共振转速计算值与试验值的误差小于5%,精度满足其工程应用要求。

5 围带减薄后的叶片频率分析

为了研究围带厚度对频率的影响,同时为了验证上述方法的可靠性,笔者将围带减薄7 mm,再次进行叶片的频率分析和频率试验。

首先进行叶片静态结构分析,获得围带减薄7 mm后,叶片中间面M1、围带面M2的法向压力F,同时整理围带减薄前后的法向压力F数据,得到两种不同围带厚度的接触面法向压力F与转速之间的关系曲线,如图14所示。

图14 法向压力F与转速之间的关系曲线

根据式(3)分析可知:法向刚度kn和切向刚度kd与法向压力F为正比关系。因此,由图14可知:围带减薄7 mm后,中间面M1的接触刚度相对变小了,而围带面M2的接触刚度相对增大了。

笔者取同样的刚度修正系数η=10,计算了接触面的法向刚度kn和切向刚度kd。

中间面M1接触刚度如表6所示。

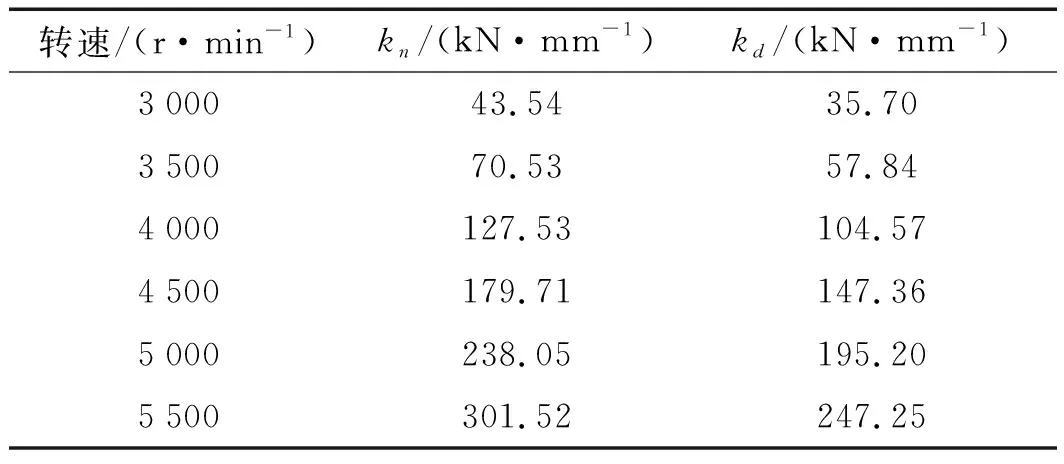
表6 中间面M1接触刚度

围带面M2接触刚度如表7所示。

表7 围带面M2接触刚度

根据表(6,7)的接触刚度,笔者进行叶片频率分析,得到围带减薄7 mm后叶片的振动频率数据,如表8所示。

表8 围带减薄后叶片1阶节径振动频率/Hz

根据表8中的数据,笔者绘制了叶片节径振动坎贝尔图,如图15所示。

图15 围带减薄后叶片1阶节径振动坎贝尔图

根据图15可知:围带减薄7 mm后,在转速3 000 r/min～5 500 r/min区间内,不存在4节径1阶共振转速,说明减薄围带厚度是改变叶片频率的有效方法[19]。

围带减薄后,笔者再次进行叶片动频试验,获得叶片5节径1阶、6节1阶共振转速测试结果。叶片5节径1阶共振转速测试结果,如图16所示。

图16 叶片5节径1阶共振转速/(r·min-1)

叶片6节径1阶共振转速测试结果,如图17所示。

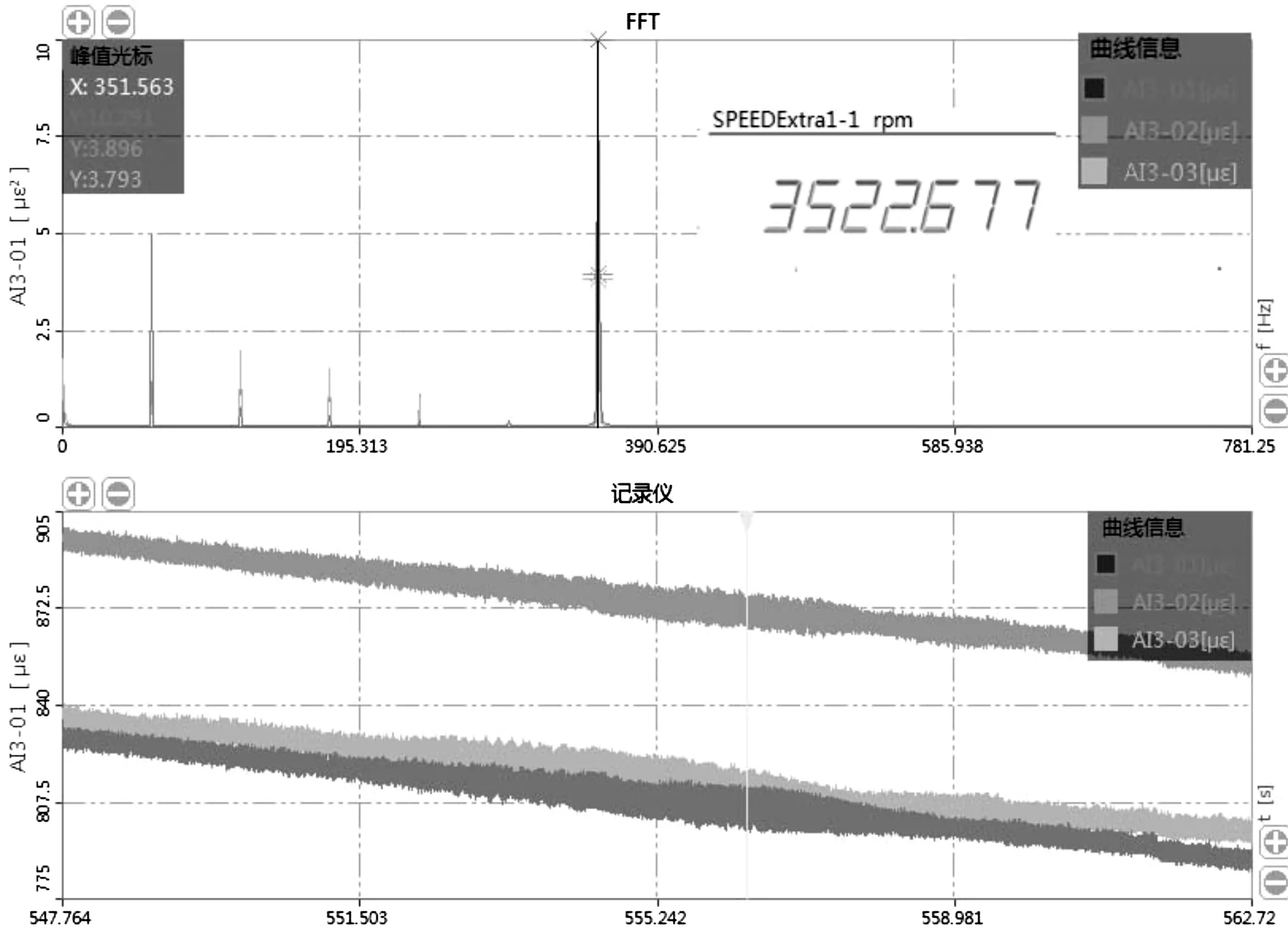
图17 叶片6节径1阶共振转速/(r·min-1)

同时,根据图15可得到叶片的5节径1阶共振转速的计算值为4 330 r/min,6节径1阶共振转速的计算值为3 531 r/min。

笔者将共振转速的计算值与试验值进行对比,其结果如表9所示。

表9 围带减薄后叶片1阶共振转速对比

由表9可知:围带厚度减薄后,共振转速计算值与试验值的误差<1%,精度满足工程应用要求。围带减薄前后,叶片1阶共振转速对,以及共振转速与额定转速的避开率如表10所示。

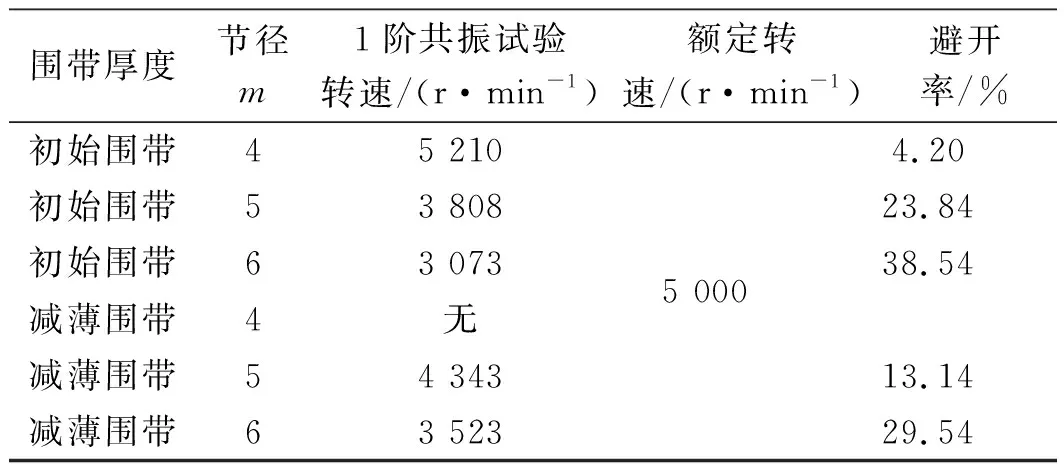
表10 叶片1阶共振试验转速避开率

由表10可知:围带减薄7 mm后,叶片的5节径、6节径1阶共振转速均比之前有所提高,但叶片共振转速与额定工作转速的避开率均>5%,由此可见,该结果是满足设计要求的。

6 结束语

笔者通过理论与试验相结合的方法,提出了一种带刚度修正系数的接触刚度计算方法,解决了工业汽轮机阻尼结构长扭叶片设计时,无法准确预测叶片共振频率的问题;同时,采用该方法对围带减薄后的叶片进行了频率分析,结果表明,叶片共振转速计算值与试验值吻合很好。

该研究结论如下:

(1)通过试验得到叶片共振频率值fe,调整刚度修正系数η,进行叶片频率分析,得到共振频率计算值fi与η的曲线;当fi与fe的误差<5%时,确定刚度修正系数η=10;

(2)采用刚度修正系数η=10计算接触刚度,进行6种不同转速的叶片频率分析,得到叶片1阶共振转速,共振转速计算值与试验值的误差<5%,精度满足工程应用要求;

(3)围带厚度减薄7 mm后,采用相同的方法进行叶片频率分析,共振转速计算值与试验值的误差<1%;该结果验证了笔者所提方法的可靠性。

随着阻尼结构长扭叶片在工业汽轮机上的推广应用,笔者后续需要对阻尼结构的振动磨损进行深入研究,特别是研究接触刚度对阻尼结构磨损的影响,以保障叶片长期安全运行。