板式电涡流TMD有限元模拟与参数优化

卢亮亮李金海杨德超

（昆明理工大学建筑工程学院，昆明 650000）

0 引言

在城市道路发展中，人行桥普遍的应用于解决人行道、车行道交汇引发的安全问题。在人行桥建设时常采用具有高强轻巧、易安装等优点的钢结构桥［1］，但其也存在轻柔与低阻尼的缺陷，导致在受到人致激励下易产生竖向的过幅振动，进而影响行人的行走舒适度［2］，严重的甚至破坏桥体结构。为提升人行桥的行走舒适度与安全性，在人行桥上加设电涡流调谐质量阻尼器（Tuned Mass Damper，TMD）是一种行之有效的方法。

传统黏滞阻尼器存在机械磨损、不易养护、阻尼与刚度耦合等缺点。相较于传统黏滞阻尼器，电涡流TMD依据电磁感应原理产生阻尼，具有耐久性、阻尼易调节、无附加刚度等优点，故电涡流TMD在土木工程领域拥有着广泛的研究和应用前景［3～5］。2001年，方重等［6］提出电磁涡流耗能TMD，并验证电磁涡流耗能TMD具有良好的阻尼减震效果；2002年，楼梦麟等［7］通过电磁耗能TMD结构减震的振动台实验，证明了电磁涡流耗能原理的TMD新装置具有良好的结构减震效率；2013年，汪志昊等［8］研制一种适用于吊杆减振的永磁式电涡流TMD，并验证该款电涡流TMD具有工程应用可行性；2016年，陈政清等［9］对一种板式电涡流TMD进行有限元仿真与参数优化，分析得出导体板厚度、气隙、永磁铁排布方式对电涡流TMD的性能有显著影响；2019年，王梁坤等［10］提出一种电涡流TMD，使用有限元软件对其永磁铁排布方式、导磁板厚度、导体板厚度、和磁导间距进行了参数分析及优化，并提出一种电涡流TMD的设计方法。

本文对本课题组提出的电涡流TMD样机进行三维有限元电磁瞬态场分析。研究永磁铁排布方式、气隙、永磁铁厚度、导体板厚度对电涡流TMD阻尼力做功的影响，并根据电涡流TMD阻尼力做功的大小随各参数变化规律，给出合理的参数设计范围，以供类似电涡流TMD研究进行参考。

1 电涡流TMD基本构造

1.1 板式电涡流阻尼器结构

依据人行桥的减震需求，本课题组拟提出一种电涡流TMD样机，结构如图1所示。

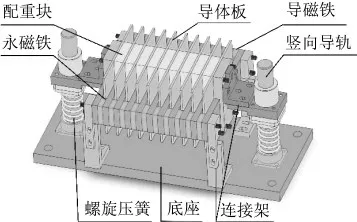
图1 电涡流TMD样机Fig.1 Eddy current TMD prototype

阻尼器结构底座用于阻尼器与被控对象连接；底座连接阻尼器两部分构件，一部分由底座通过连接架与永磁铁、导磁铁连接，该构件在被控对象受到激励后总会伴随被控对象一起运动且与被控对象不产生相对位移，故将该构件称为“固定构件”；另一部分为底座上连接竖向导轨，螺旋压簧套在摩擦力较小的竖向导轨上，导体板、配重块则通过连接构件与螺旋压簧连接，该部分构件在被控对象受到激励后由于惯性作用会保持原有状态而来不及响应，因此会与被控对象产生相对位移，故将该构件称为“活动构件”。此外，“固定构件”中的永磁铁、导磁铁与“固定构件”中的导体板、配重块在相应位置开有孔洞以插入螺杆，该设计方便调节阻尼器相关参数以达到改变阻尼力大小的目的。

当被控对象受到激励后，由于“固定构件”与“活动构件”的工作状态不同，两者产生的位移差表现为“活动构件”中的导体板在“固定构件”中的永磁铁之间做切割磁感线运动，因此导体板上的磁通量会发生改变。由楞次定律可知，导体板表面会产生类似涡流状的感应电流，这种感应电流会抑制导体板上磁通量的变化从而产生抵制导体板运动的阻尼力［11］，该阻尼力在阻尼器上提供电涡流阻尼。

由文献［8］得出电涡流TMD阻尼中摩擦阻尼为机构固有阻尼，其大小由机构本身决定，故本文暂不讨论固有阻尼部分。再者，机构中螺旋压簧为弹性元件，其提供弹性阻尼。至今传统阻尼器以及黏弹性阻尼中对弹性元件设计很成熟，故本文不再赘述。电涡流TMD阻尼核心为可调节的电涡流阻尼系统，是电涡流TMD产生阻尼的主要部分，该部分主要由永磁铁、导磁铁、导体板构成，因此阻尼系统可通过调节气隙（永磁铁表面到导体板表面距离）、永磁铁厚度、导体板厚度等来实现对阻尼器性能的调节。综上所述，本文通过选取电涡流TMD中的阻尼系统部分研究各参数对阻尼器的影响。

1.2 电磁场基本方程

麦克斯韦方程组是描述电磁场的基本方程，在有限元仿真模拟中需将麦克斯韦方程组推导成微分形式：

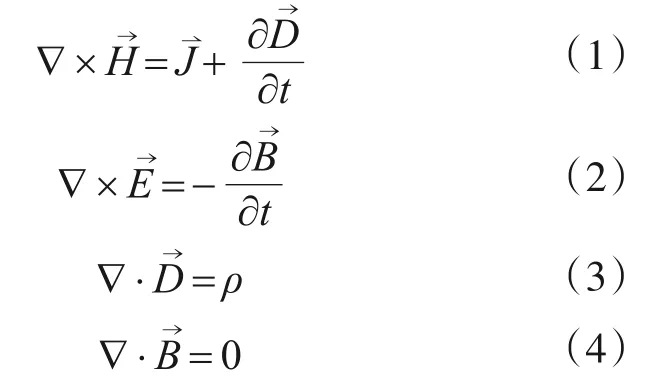
式中：H为磁场强度；E为电场强度；J为传导电流密度；D为电通密度；B为磁感应强度；ρ为电荷体密度。

式（1）—式（4）中场量E、D、B、H之间的关系由媒介的特性决定，对于线性媒介，其关系为

式中：ε为介质的介电常数；μ为介质的磁导率；σ为介质的电导率。

在ansoft三维瞬态场中采用T-Ω算法和局部剖分法对三维瞬态运动经行电磁场计算。而在计算低频瞬态磁场时麦克斯韦方程组微分形式可写成：

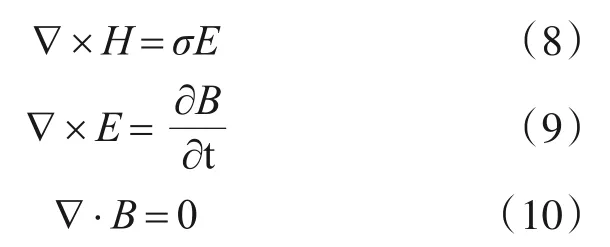
通过式（8）、式（9）、式（10）可以得出以下恒等式：

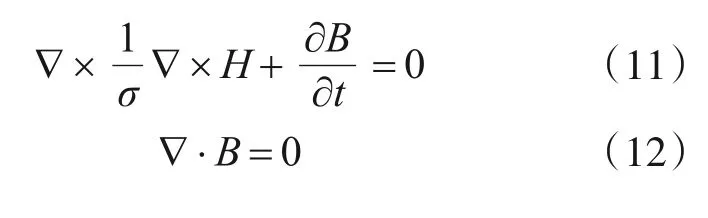
1.3 电涡流TMD模型简化及磁极分布方案

根据1.1小节可知，本文需分析主要由导体板、永磁铁、导磁铁构成的电涡流TMD阻尼系统模型，利用有限元软件ansoft建立该模型如图2所示。

图2 阻尼系统模型Fig.2 Damping system model

阻尼系统构件尺寸参数如表1所示。

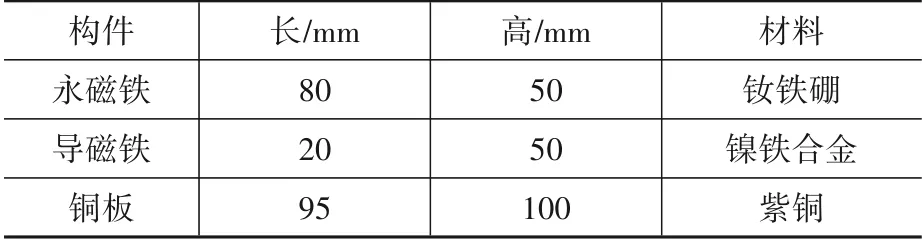
表1 阻尼系统构件尺寸参数Table 1 Component size parameters of damping system

永磁铁选用稀土永磁铁钕磁铁（Nd2Fe14B），其牌号为N35，剩磁感应强度Br=1170～1210MT，矫顽力为868 kA/m，内禀矫顽力为955 kA/m，最大磁能积为263 kJ/m3，总布置块数22块；导磁铁的相对磁导率为2 000；铜板相对磁导率为0.999，电导率为58 000 000 s/m。

从图2中看出永磁铁分布呈几何对称，定义两侧磁铁分别为左侧磁铁、右侧磁铁，由于永磁铁磁极分布的不同，磁路长短不一，根据磁路欧姆定律可知，磁路短，磁动势大，磁通量大，从而导体板表面磁感应强度大，因此选择不同的磁极分布对阻尼系统有很大影响。通过拟定不同磁极分布方案来选择最佳磁极分布方案，磁极分布方案如表2所示，各方案示意如图3表示。

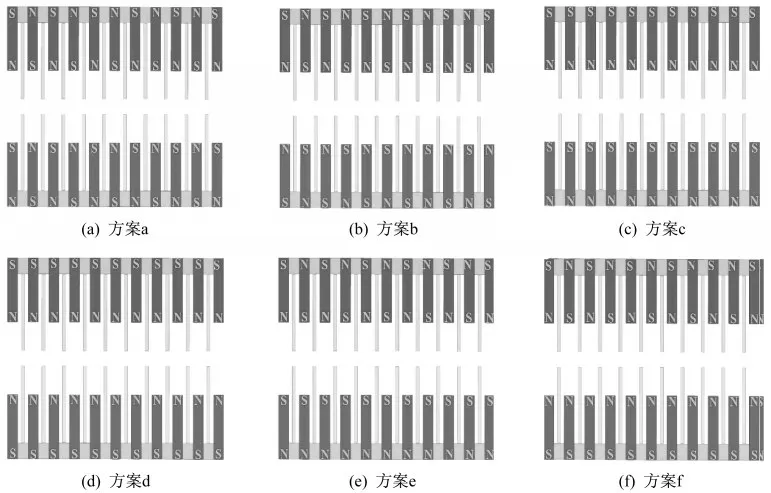
图3 永磁铁磁极分布图Fig.3 Permanent magnet pole distribution diagram

表2 永磁铁分布方案Table 2 Permanent magnet distribution scheme

阻尼系统中暂取永磁铁厚度为15 mm，导体板厚度为5 mm，气隙宽度为5 mm，导磁铁厚度为15 mm，其他各项材料及参数设置参照表1所示，根据表2中各磁极分布方案，利用有限元建模进行分析。以人行桥减震为例，人致振动为人行桥主要激励，行人激励可以用傅立叶级数表达为静荷载与几个简谐动荷载叠加[12]：

式中：W为静荷载；fp为行人的步频；φi为初始相位。

由人致激励可看作周期激励，故人行桥的振动位移函数为［13］

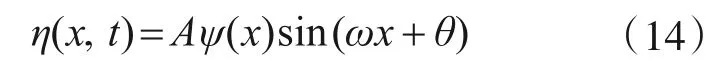
在人行桥受到激励后，加设在人行桥上的电涡流TMD随着人行桥进行周期性振动，并且其中的“固定构件”与“活动构件”也产生周期性的相对运动，从而导体板相对于永磁铁做切割磁感线运动。根据振动位移函数及电涡流TMD的工作原理，导体板相对永磁铁的速度函数可为含有余弦的函数，为方便计算，在进行有限元模拟时将其速度函数简化为

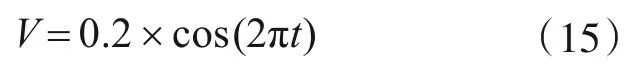
在人行桥受到激励后，其振动能量传递到电涡流TMD上，电涡流TMD通过电磁感应产生抑制导体板运动的阻尼力，最终能量由阻尼力对内做功而逐渐耗散，以达到减震目的。故本文以电涡流阻尼力在一段时间内所做的功来判断阻尼系统工作性能。

通过有限元模拟结果可得到在时间t为2 s内阻尼力Fz和导体板的位移S的变化曲线。以方案a为例，Fz随时间变化曲线如图4所示，导体板位置S随时间变化曲线如图5所示。

图4 阻尼力随时间变化曲线Fig.4 Damping force versus time curve

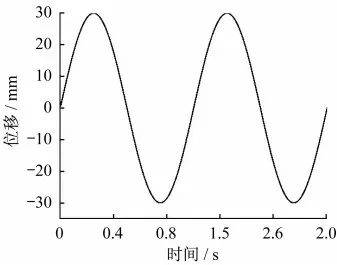
图5 导体板位置随时间变化曲线Fig.5 Conductor plate position versus time curve

通过有限元模拟可得阻尼力Fz在时间步长Δt=0.01上的平均值及时间步长Δt上的位移值ΔSi，在经过时间t=2 s阻尼力做功W为

阻尼力在铜板运动过程中的功即为阻尼系统通过热量耗散的能量。将各方案模拟结果通过计算阻尼力做功得到的结果如表3所示。

从表3中可以看出，不同的磁极分布对阻尼力做功影响很大，选用合适的磁极分布能有效提高阻尼系统工作效率；当磁铁磁极交错分布时相较于磁铁磁极同向分布时方案阻尼力做的功更大，因为磁极交交替分布下，磁路短，磁动势损耗较少［14］，产生的阻尼力更大。选择磁极交替分布的方案进行对比可以得出：方案a、b阻尼力做功几乎为方案e、f的两倍。综上所述，电涡流TMD采用两侧永磁铁交替分布时性能最佳。

1.4 阻尼系统模型简化

通过1.3小节分析得，永磁铁采用磁极交替方案有效提高阻尼器性能。方案a与方案b磁极分布皆采用磁极交替分布，但两侧相对磁极分布不同。为研究两侧永磁铁磁极之间相互影响的关系，将方案a、b，c、d，e、f组合为两两首块磁铁磁极不同的方案组。通过对比各方案组阻尼力做功的差值及差值占比，结果如表4所示。

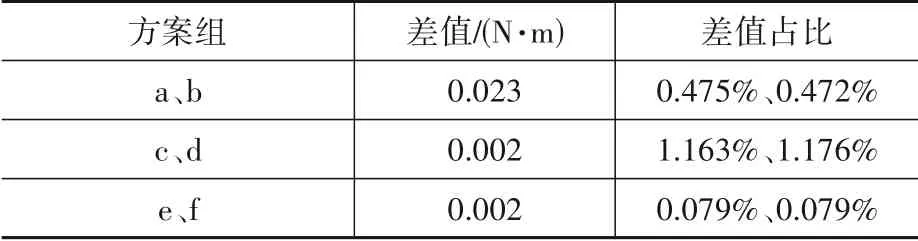
表4 差值及差值占比Table 4 Difference and ratio of difference

从表4可以看出方案组中的各方案组内阻尼力做功差值不大，且各差值占对应方案的比重不大，由此可知两侧永磁铁磁极之间相互作用不大，其原因为两侧磁铁磁极之间的间距远大于气隙，单侧磁铁磁极之间相互作用远大于两侧磁铁磁极之间的相互作用，从磁力线分布可明显观察到该现象。以方案a为例，得到阻尼系统磁力线分布如图6所示。

图6 阻尼系统磁力线分布Fig.6 Distribution of magnetic field lines of damping system

从图6看出两相邻磁铁之间磁力线相较于两侧磁铁之间磁力线更密集，因此两侧磁极之间相互影响不大。在永磁铁磁极交替分布下，两侧永磁铁及其磁力线分布均呈几何对称，故可将阻尼系统模型进一步简化。

为便于有限元模拟仿真，由阻尼系统两侧磁铁之间相互影响可忽略，故将阻尼系统简化为图7所示的简化模型。

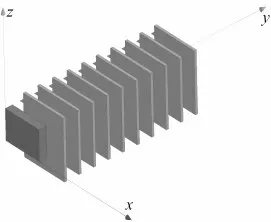
图7 简化模型Fig.7 Simplified model

为验证简化模型可行性且其与阻尼系统模型的关系。暂取导体板厚度为5 mm、气隙为5 mm，永磁铁厚度为15 mm建立简化模型与阻尼系统模型并进行有限元模拟。在时间节点t=1 s时简化模型导体板表面磁感应强度分布云图如图8所示，阻尼系统导体板表面磁感应强度分布云图如图9所示，在该时刻两模型首块导体板表面沿x轴向中线上磁感应强度对比曲线如图10所示。

图9 阻尼系统模型磁感应分布云图Fig.9 Magnetic induction distribution cloud map of damping system model

结合图8—图10可以看出，阻尼系统中两侧导体板表面的磁感应强度分布呈轴对称且任一侧磁感应强度分布于简化模型的基本相同，简化模型与阻尼系统模型中线上的磁感应强度分布在前半部分的基本一致且最大磁感应强度位置也相同。综上所述，简化模型可替代阻尼器模型进行分析。阻尼系统模型与简化模型的阻尼力做功对比如表5所示。

表5 两模型做功对比Table 5 Comparison of two models

图8 简化模型磁感应分布云图Fig.8 Magnetic induction distribution cloud map of simplified model

图10 中线上磁感应强度对比Fig.10 Comparison of magnetic induction intensity on centerline

根据表5可以看出，阻尼系统模型阻尼力做功大小几乎为简化模型阻尼力做功的两倍。下文均采用简化模型代替阻尼系统模型来分析阻尼系统中主要参数对阻尼力做功的影响。

2 阻尼系统参数分析及优化

2.1 影响参数及工况

根据1.4小节可将电涡流阻尼系统简化为简化模型分析。根据电涡流TMD阻尼系统结构可知，导体板厚度、永磁铁厚度、气隙是影响阻尼力做功的主要因素，故设置三个不同参数的模拟变量，各参数取值如表6所示。

表6 参数取值Table 6 Parameter value mm

由1.2小节中给出阻尼系统相关尺寸及材料参数，以此为基准参照表6建立不同主要参数变化下的简化模型。考虑到不同工况下阻尼力做功的大小不同，为方便分析各参数对阻尼力做功的影响，通过待定系数法，观察其余两参数变化对阻尼力做功的影响。

2.2 气隙的影响分析

通过固定导体板厚度，模拟各永磁铁厚度下阻尼力做功的大小随气隙变化规律。为便于分析，研究在固定导体板厚度da=12 mm下阻尼力做功的大小随气隙变化规律，如图11所示。

图11 阻尼力做功随气隙变化Fig.11 Variations of damping force work with air gap

从图11可以看出，在给定区间内，阻尼力做功的大小随气隙呈负指数衰减：随着db增大，阻尼力做功变少，且随着db增大到一定值后有趋于稳定的迹象。出现该现象的原因是db过大，两磁铁之间相互作用较少且间距较长故而漏磁较为严重，从而导致导体板上的磁感应强度变化不明显。为分析在给定区间内阻尼力做功的大小随气隙变化的变化率，对图11中各曲线数据采用指数型回归得各回归方程：Yi，并对该回归方程求导得到各导函数为：H(x)=导函数图线如图12所示。

图12 不同气隙下阻尼力做功的变化率Fig.12 Variation rate of damping force work under different air gaps

从图12中可以看出在db＜7 mm时，db变化对阻尼力做功的变化率的影响较大。当db＞7 mm时，随着db变化对阻尼力做功的变化率的影响较小，而且当db增大到一定程度后阻尼力做功的变化率基本保持不变。

综上所述，当气隙取值大于7 mm后，导体板上已出现明显漏磁，通过改变气隙宽度对阻尼系统工作影响不大，因此建议气隙取值在7 mm以内。特别在永磁铁厚度越大该变化越明显，而在永磁铁厚度较小时，db变化对阻尼力做功影响较小。

2.3 永磁铁厚度的影响及分析

通过待定系数法，通过固定气隙而改变永磁铁厚度来分析永磁铁厚度变化对阻尼力做功的影响。为便于分析，故此处取导体板厚度da=12 mm来分析阻尼力做功随永磁铁厚度变化规律如图13所示。

图13 阻尼力做功随永磁铁厚度变化Fig.13 Variation of damping force work with permanent magnet thickness

从图13可以看出，阻尼力做功的大小随永磁铁厚度呈对数增大：当永磁铁厚度增大，阻尼力做功增大，当气隙越小时，阻尼力做功的大小随永磁铁厚度变化越明显。为分析在给定区间内不同永磁铁厚度对阻尼力做功的大小的影响，将各曲线数据按照对数回归模型得到各回归方程：Ti。通过回归方程的导数来分析其变化率，其导函数为：G(x)=。导函数曲线如图14所示。

图14 不同永磁铁厚度下阻尼力做功的变化率Fig.14 Variation rate of damping force work under different permanent magnet thickness

从图14可以看出阻尼力做功的变化率随着永磁铁厚度变大而逐渐变小，在永磁铁厚度c＜15 mm时阻尼力做功变化率下降较快且较为明显，在c＞15 mm时，随着永磁铁厚度增大，虽然阻尼力作做功的大小在增大，但其改变量基本保持不变，其原因是由于永磁铁厚度增大，永磁铁自身磁阻也增大，相应需要一部分磁动势来抵消自身磁阻［15］，因此阻尼力做功的大小随永磁铁厚度变化的增率趋于稳定。综上所述，永磁铁厚度取15 mm以内变化较为合适，在此继续增大永磁铁厚度后虽然阻尼力做功的大小有所提升，但整体提升不大，有可能经济性下降。

2.4 导体板厚度的影响及分析

为分析阻尼系统中阻尼力做功的大小随导体板厚度变化规律，此处选用当永磁铁厚度c=9 mm时分析，得到其变化规律如图15所示。

图15 阻尼力做功随导体板厚度变化Fig.15 Variation of damping force work with conductor plate thickness

从图15可以看出阻尼力做功的大小随着导体板厚度呈指数增大：随着导体板厚度增大而增加。将图15中各曲线数据按照指数型回归得到各曲线回归方程Ui，通过分析回归方程的导函数L(x)=得到阻尼力做功的大小随导体板厚度改变的变化率如图16所示。

图16 不同导体板厚度阻尼力做功的变化率Fig.16 Variation rate of damping force work under different conductor plate thickness

从图16中可以看出，随着导体板厚度增大，阻尼力做功的增率也增大，而当气隙较大时，增大导体板厚度，阻尼力做功的提升不大。在确定其他参数时，由于导体板厚度越大，阻尼力做功越大，因此建议在给定区间内导体板厚度选择最值。

3 结论

通过有限元软件三维电磁场分析各主要参数对电涡流TMD影响得到结论如下：

（1）不同的永磁铁磁极分布方式对阻尼力做功有着显著影响。当阻尼系统采用永磁铁磁极交替分布时，阻尼力做功的大小最大。

（2）阻尼系统结构呈几何对称；两边导体板表面磁感应强度分布之间也呈几何对称；磁力线走势呈中心对称；依据整体模型阻尼力做功的大小为简化模型的两倍关系，可由简化模型代替阻尼系统模型分析。

（3）运用待定系数法、线性回归以及回归方程的导数分析各参数对阻尼力做功的影响可得：气隙db在7 mm以内、永磁铁厚度取15 mm以内最优，导体板厚度在可选区间取最值。