基于实测强震记录的主余震向量过程降维模拟
刘子心,姜云木,刘章军,阮鑫鑫
(1.防灾科技学院中国地震局建筑物破坏机理与防御重点实验室,河北三河 065201;2.武汉工程大学土木工程与建筑学院,湖北武汉 430074)
引言
研究表明,地震动不仅具有较强的随机性,同时具有明显的序列性,即在一次主震后往往会伴随着多次余震的发生,例如2008年汶川地震,在主震后共发生了13 718次余震,且余震最高震级达6.5级。由此可见,余震不仅数量较多,且部分震级较大,成为结构二次破坏的主要因素。然而,由于主余震型地震动实测记录数量有限,且需要对实测强震记录进行一定处理才能满足结构抗震分析的需求,因此,采用人工合成方法生成主余震型地震动时程近年来受到了广泛关注。
为了构造主余震型地震动,近年来学者们开展了对主余震参数关系的研究。欧进萍等[1]根据49 组主余震震级资料,线性回归了主余震间震级的经验公式;周昱辰等[2]利用芦山的实测主余震强震记录,研究了4 种地震预警震级估计参数随震级与时间的变化趋势;Zhang 等[3]以线性回归的方式,较为全面地研究了主余震间在持时、幅值和频谱方面的关系。上述研究为人工合成主余震型地震动奠定了良好基础。一般来说,主余震型地震动的人工合成方法大致可分为确定性方法与随机方法两大类。对于确定性方法,Hatzigeorgiou等[4]提出了采用重复法构造主余震序列,该方法假设主余震的特性一致,但这明显不符合实际状况;Li 等[5]提出了随机组合法构造主余震序列,即从主震和余震记录库中分别随机挑选出一条地震动记录组合成主余震序列,然而,该方法得到的主余震序列在本质上不具有随机性。对于随机方法,Hu等[6]利用调幅过滤白噪声方法生成主震过程,再根据分支余震序列法生成余震。然而,该方法属于Monte Carlo 方法,无法在概率层面上精确描述主余震过程;姜云木等[7]基于Copula 函数,建立了主余震参数的相关结构,并引入正交随机变量的随机函数方法,从而实现了给定主震参数条件下余震的高效模拟。然而,该研究采用了时-频全非平稳演变功率谱模型,由于该模型在时频域相互耦合,因此在识别主余震参数时不可避免地引入了误差。同时,该研究将主余震型地震动视为2 个相互独立的随机过程,并没有考虑主余震间的相干性,需要进行2 次模拟才能得到主余震型代表性时程。综上可见,亟需发展一种能够在概率层面上一体化高效模拟主余震型地震动的方法。
为此,本研究将主余震型地震动视作一个随机向量过程。首先,根据实测强震记录,建立了主余震相干函数模型;其次,根据地震动的能量曲线与反应谱,对主余震的演变功率谱模型参数进行识别,并给出了对应不同场地的所有参数取值;最后,结合基于本征正交分解(POD)的随机函数方法[8-9],实现了主余震向量过程的降维模拟。数值算例验证了主余震相干函数模型的正确性以及参数识别方法的有效性。值得说明的是,采用随机函数-降维模拟方法生成的每一条主余震型代表性时程均具有赋得概率,且代表性时程集合构成一个完备的概率集,因此可与概率密度演化方法[10-11]相结合,实现复杂工程结构在主余震作用下的精细化动力响应与可靠性分析。
1 主余震实测强震记录的选取
文中从美国太平洋地震工程研究中心(PEER)的NGA-West2数据库和中国国家地震科学数据共享中心(CSMNC)中筛选了20 次地震的488 组主余震实测记录,基本信息如表1 所示。主余震记录的筛选原则如下[12]:
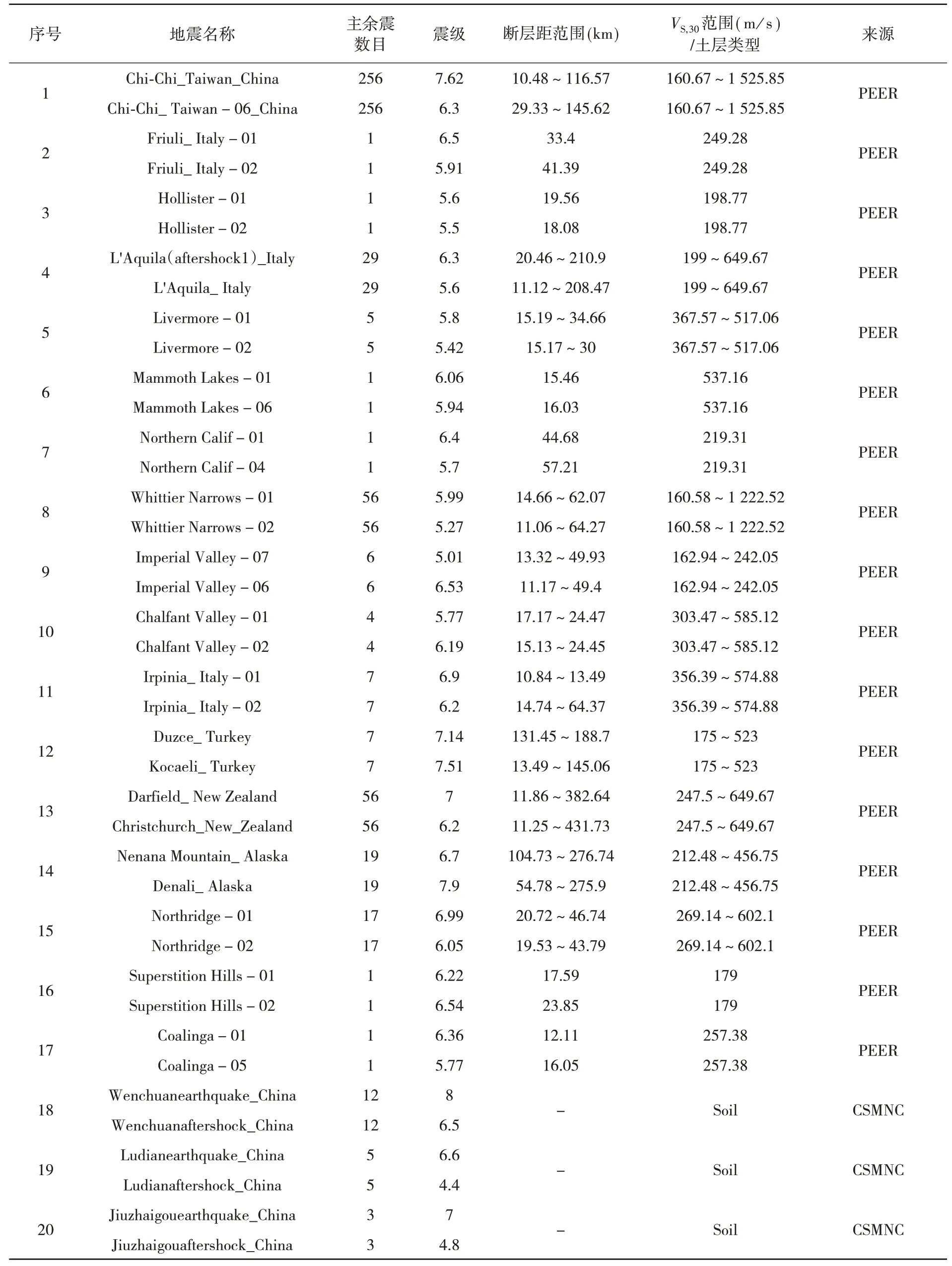
表1 选取的主余震实测记录基本信息[7]Table 1 The basic information of the measured main-aftershock records selected in this paper
(1)主震记录与其对应的余震记录必须来自同一台站;
(2)仅选取与主震对应且震级最大的余震作为研究对象;
(3)断层距离应大于10 km,以减少近场效应的影响;
(4)主震与余震的震级均应大于4,以排除对结构影响较小的地震动。
PEER 数据库提供了VS,30作为场地划分的依据,同时,文献[13]给出了《中国地震动参数区划图》(GB 18306-2015)[14]中5 种场地类别与VS,30的对应关系。然而,与PEER 数据库不同,CSMNC 数据库仅以Rock或Soil区分场地。根据《建筑抗震设计规范》(GB 50011-2010)[15]中对场地的描述,文献[16]建议Rock对应Ⅱ类场地,Soil对应Ⅲ类场地。综上,文中选用的主余震实测记录的场地类别与VS,30及地震数量的对应关系如表2所示。

表2 对应于不同场地类别的VS,30 范围及实测记录数量[13]Table 2 The range of VS,30 and number of measured motion records corresponding to different site classifications
为保证实测强震记录能够满足分析需求,还需对其进行基线校正和四阶Butterworth 滤波处理,以及在1%~99%的能量范围内进行截取。
2 主余震的相干性分析
众所周知,局部场地对地震动的频谱特性有较大影响,而同一台站记录的主震和余震发生于同一局部场地,由此推知,主余震在频谱特性上可能存在着某种相干性。为此,根据筛选的488 组实测强震记录,对主震与余震之间的相干性进行统计分析。为简便起,将主震和余震均视为平稳过程,则(迟滞)相干函数定义为:

式中:Sma(ω)为主震和余震过程的互功率谱密度函数;Sm(ω)与Sa(ω)分别为主震和余震过程的自功率谱密度函数。
对于任意一组主余震实测强震记录,采用MATLAB 工具箱自带的“cpsd”函数计算主余震的互功率谱,以及“pwelch”函数分别计算主震和余震的自功率谱,利用式(1)即可得到每组实测主余震的相干函数。图1给出了II类和III类场地类别中典型主余震实测记录的相干函数曲线。
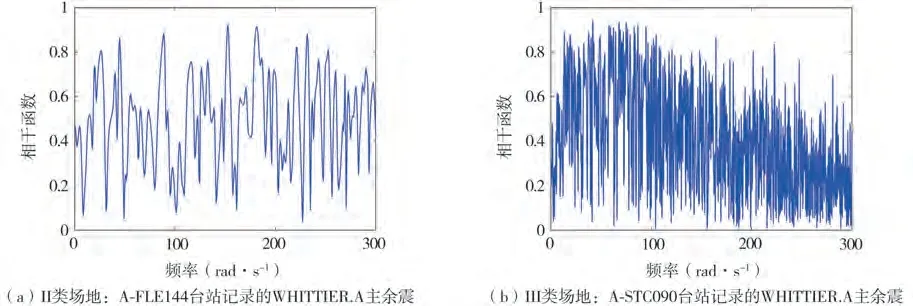
图1 II类和III类场地类别中典型主余震实测记录相干函数Fig.1 Typical coherence function of the measured main-aftershock records for soil site classifications II and III
从图1可知,在工程常用的频率范围(0~300) rad/s内,主余震的相干性总体上随着频率的增加呈现递减趋势。为此,可采用前三阶傅里叶级数模型对主余震的(迟滞)相干函数进行拟合,即:
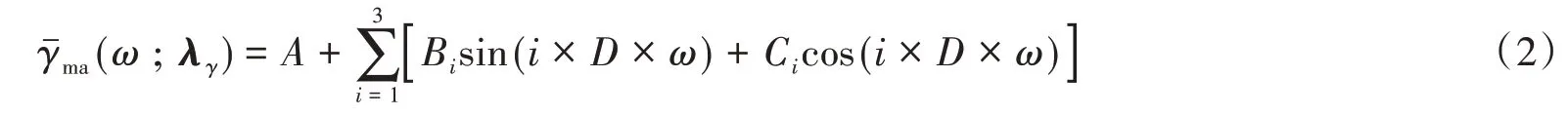
式中,λγ=(A,B1,C1,B2,C2,B3,C3,D)为傅里叶级数模型的参数向量。
在计算主余震的相干函数时,将每一组实测主余震记录视作一个随机过程,分别计算488组实测主余震记录的相干函数,进而得到它们的均值相干函数曲线,并根据最佳平方逼近原则,以γma(ω)为目标值,对傅里叶级数模型的参数向量λγ进行识别,即:
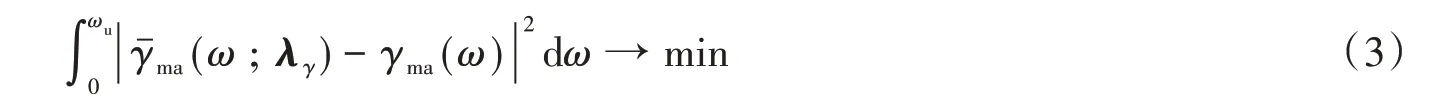
式中,截断频率ωu=300 rad/s。傅里叶级数模型参数向量λγ的识别结果如表3所示。
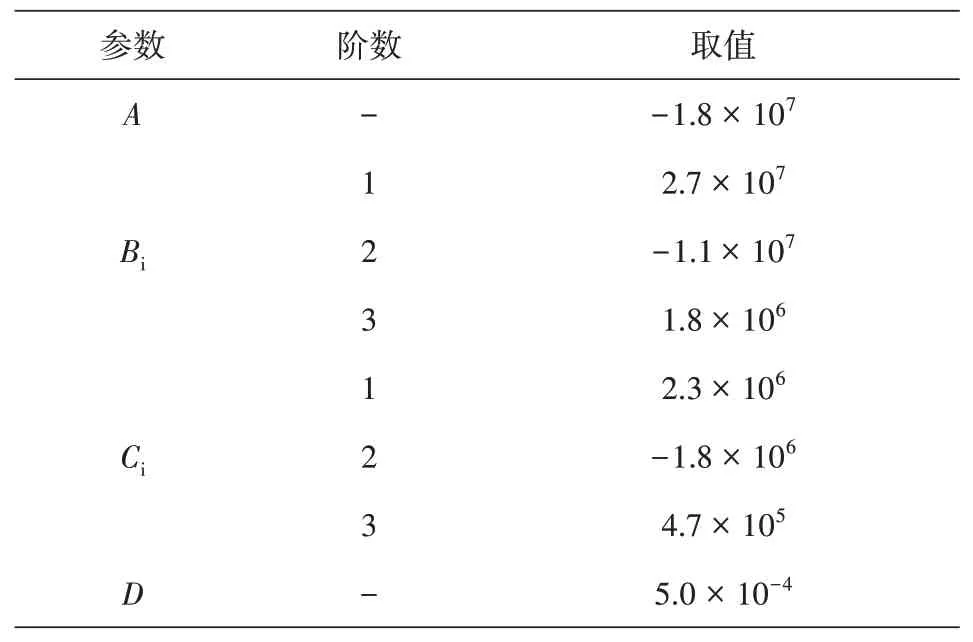
表3 傅里叶级数模型的参数取值Table 3 Parameter values of the Fourier series model
进一步,傅里叶级数模型与主余震实测记录(迟滞)相干函数的拟合结果如图2所示。
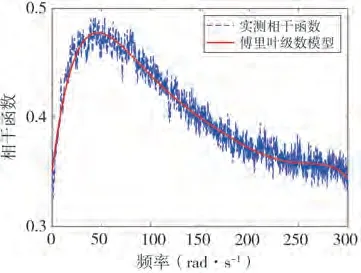
图2 相干函数模型与实测记录的拟合结果Fig.2 Fitting result between the coherence function model and the measured records
需要说明的是,文中并未对相干函数进行场地类别分组处理,这是由于每一组实测主余震记录均来自同一台站,因此场地差异性对主余震相干性的影响可以忽略。
3 主余震过程的模型参数识别
3.1 非平稳地震动过程的演变功率谱模型
为简便起见,文中采用强度调制的演变功率谱密度函数形式[17]:
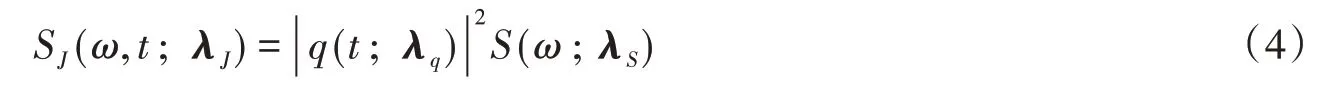
式中:SJ(ω,t;λJ)为非平稳地震动过程的单边演变功率谱密度函数;q(t;λq)为强度调制函数;S(ω;λS)为平稳地震动过程的单边功率谱密度函数。
对于强度调制函数,采用Amin-Ang提出的三段式模型,该模型反映了地震动过程的上升段、平稳段和衰减段,其表达式为[18]:
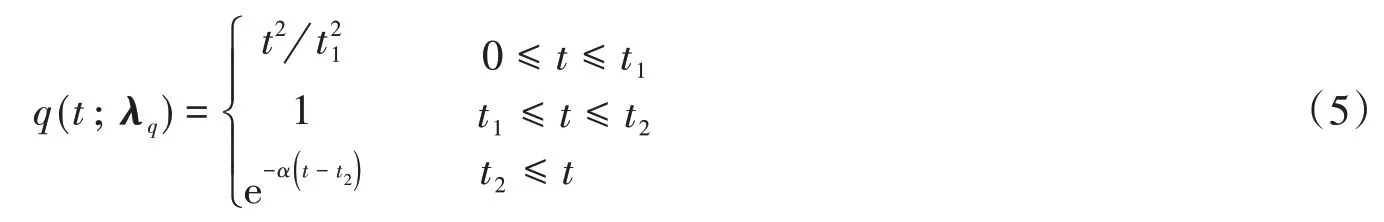
式中,λq=(t1,t2,α)为强度调制函数q(t;λq)的参数向量。对于平稳地震动过程的单边功率谱密度函数,采用经典的Clough-Penzien模型[19]:
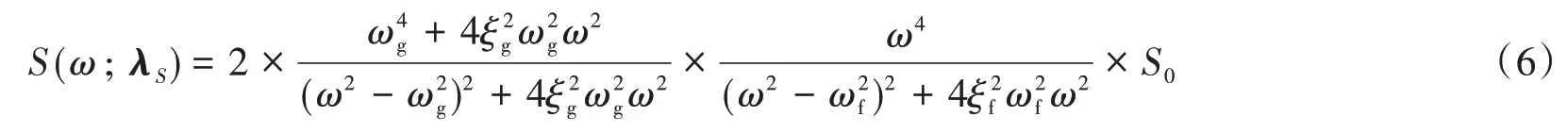
式中
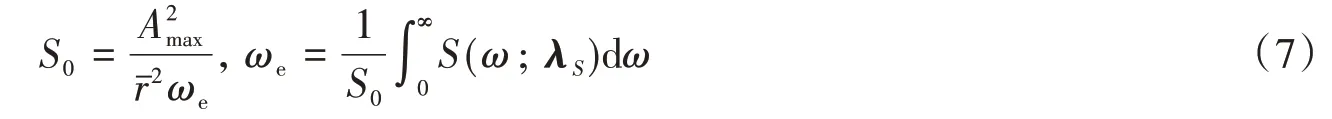
式中:ωg和ξg分别为场地土的卓越圆频率和阻尼比;ωf和ξf分别为基岩的卓越圆频率和阻尼比。一般地,可取ωf=0.1ωg,ξf=ξg。Amax为地震动峰值加速度的均值,为峰值因子。λS=为平稳地震动过程功率谱S(ω;λS)的参数向量。
由此,非平稳地震动过程的演变功率谱SJ(ω,t;λJ)的参数向量为

3.2 演变功率谱模型的参数识别
对于第i条实测强震记录ai(t),其随时间变化的归一化能量曲线Ii(t)可表示为[20]:

式中,Ti为第i条实测强震记录的持时。
对于非平稳地震动过程,其随时间变化的归一化模型能量曲线PJ(t;λJ)为:
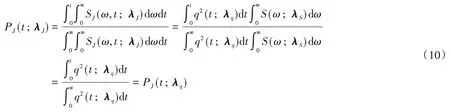
根据式(9)与式(10),以Ii(t)为目标值,采用最佳平方逼近原则,便可对参数向量λq,i进行识别:

由此,即可得到与第i条实测强震记录相对应的强度调制函数参数向量λq,i=(t1,i,t2,i,αi)。
为了对平稳地震动过程功率谱S(ω;λS)的参数向量进行识别,首先,根据帕萨瓦尔定理,即信号在时域与频域上的总能量相等,可得:
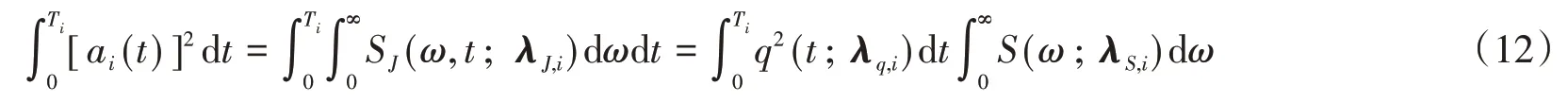
同时,令

于是,由式(12)和式(13)得到:
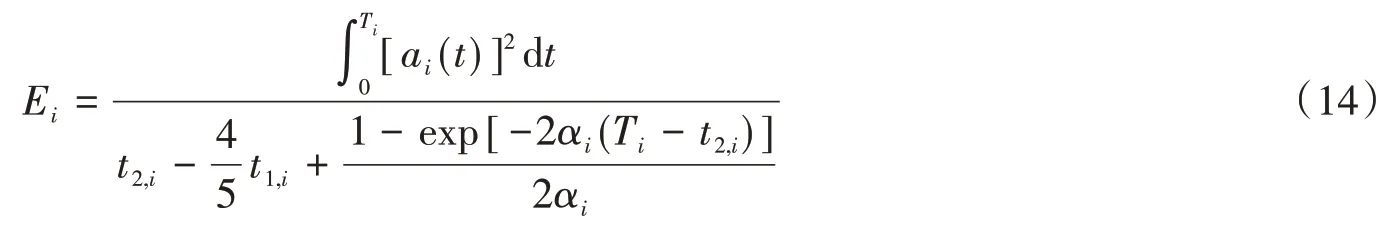
对于式(13),结合式(7)推导可知:

由于第i条实测强震记录ai(t)的峰值加速度Amax,i是已知的,这样,将所得的参数向量λq,i代入式(14)和式(15)中,即可得到与实测强震记录ai(t)所对应的峰值因子。
对于平稳地震动功率谱的场地参数,可采用拟合反应谱的方法来识别。为简便起见,在对场地参数进行识别时,将地震动视为等效平稳过程。
Vanmarcke将随机过程的反应谱定义为单质点体系反应峰值系数的平均值与反应均方差的乘积[21]。由此,对于第i条实测强震记录ai(t),其反应谱与功率谱的转换公式为:
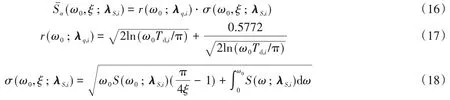
式中:r(ω0;λq,i)为等效平稳过程峰值系数的平均值;σ(ω0,ξ;λS,i)为等效平稳过程的反应均方差。ω0与ξ分别为结构的固有圆频率和阻尼比,在文中ω0≥1.05 rad/s,ξ=0.05;Td,i为等效平稳过程的持续时间,即强度超过峰值50%的持续时间,对于三段式强度调制模型,Td,i的表达式为:

最后,以实测强震记录ai(t)的前6 s反应谱Sa,i(ω0)为目标值,根据式(16),采用最佳平方逼近原则,对参数向量λS,i进行识别:
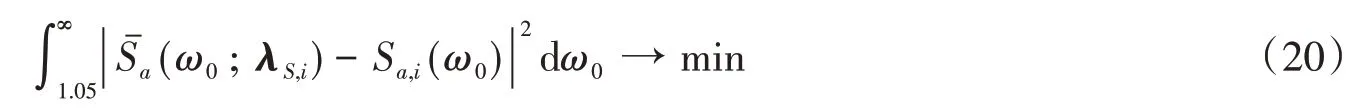
由此可以得到功率谱模型的场地参数ωg,i和ξg,i。这样,非平稳地震动过程的演变功率谱SJ(ω,t;λJ,i)的参数向量λJ,i识别完成。
进一步,文中引入了R2(决定系数)作为参数识别效果的衡量标准。任意一组待拟合数据y的R2可定义为[22]:

式中:M为待拟合数据y的总数据点数;分别为待拟合数据的均值和拟合数据。一般地,若R2越趋近于1,则拟合效果越好。
最后,对于非平稳主余震型向量过程J(t)=(J1,J2)=(m,a),元素J1和J2分别代表主震过程和余震过程,将主震参数和余震参数分别代入式(4)中,即可得到主震过程和余震过程的演变功率谱密度函数。
现以TCU104 台站记录的CHICHI 主余震为例,根据式(11)与式(20),反应谱和地震动归一化能量的拟合结果分别如图3 与图4 所示。从图3 和图4 可以看出,无论是主震还是余震过程,模型与实测记录均拟合良好。
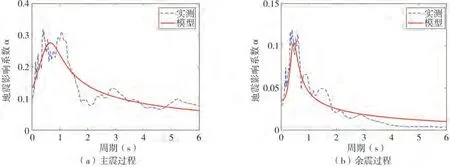
图3 反应谱拟合结果Fig.3 Fitting result of response spectrum
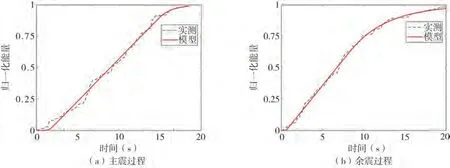
图4 地震动归-化能量拟合结果Fig.4 Fitting result of ground motion normalized energy
上述主余震典型实例的参数识别结果如表4所示。

表4 TCU104台站记录CHICHI主余震参数识别结果以及误差Table 4 Parameter identification results and error of CHICHI main aftershocks recorded by TCU104 station
可以看出,主余震型地震动的反应谱和归一化能量曲线的R2均趋近于1,说明了文中参数识别方法的有效性。
类似地,利用主余震实测强震记录,即可对主余震的演变功率谱模型参数向量λJ进行识别。根据不同场地类别的主余震实测强震记录,应用最佳平方逼近对主余震向量过程的演变功率谱模型进行参数识别,并求得每个参数的均值,将其作为主余震向量过程的演变功率谱模型参数的建议取值,具体如表5所示。
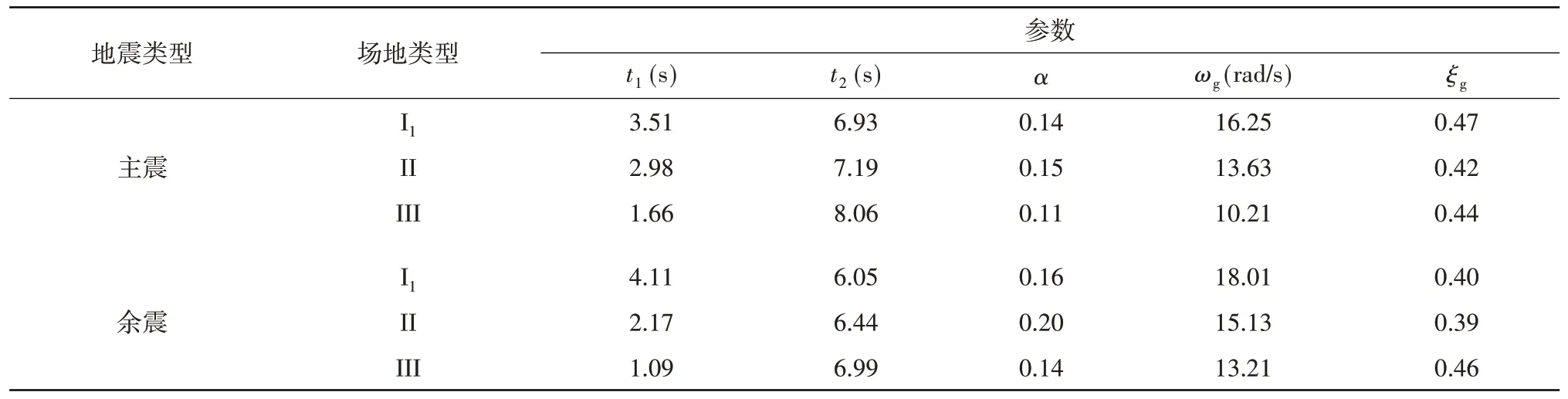
表5 不同场地类别主余震演变功率谱参数建议取值Table 5 Recommended values of main-aftershock evolutionary power spectrum parameters for different soil site classifications
同样,对于峰值加速度和峰值因子,计算488 组主余震实测强震记录的峰值加速度比值和峰值因子比值,并取均值。具体结果如表6所示。
需要说明的是,由于I0和IV类场地实测强震记录数量过少,因此没有对这两类场地进行分析。通过表5 和表6可以看出,相较于余震,主震持时更长,能量更高,场地土卓越频率更小;不同场地相比,随着土质变软,持时更长,而场地土卓越频率更小。
根据表5和表6,便可实现对主余震演变功率谱的建模。

表6 主余震幅值参数比值Table 6 Main-aftershock amplitude parameter ratio
4 基于POD的主余震向量过程降维模拟
4.1 基于正交随机变量的POD表达
对于主余震型地震动过程,可将其视作一个零均值的1D-2V(一维双变量)随机向量过程,因此可采用本征正交分解(POD)方法进行模拟。非平稳主余震向量过程J(t)=(J1,J2)=(m,a)的演变功率谱密度矩阵SJ(ω,t)为:

根据文献[9],主余震的演变功率谱矩阵SJ(ω,t)可分解为如下形式:

式中:上角标*和T分别表示复共轭和矩阵转置;D(ω,t)为对角矩阵,即D(ω,t)=;γ(ω)为主余震的相干函数矩阵:

主余震的相干函数矩阵γ(ω)是一个非负定的Hermitian 矩阵,其元素可由式(2)得到。对相干函数矩阵γ(ω)进行特征分解,即可得到:

式中:特征向量矩阵Ψ(ω)=[ψ1(ω),ψ2(ω)];特征值对角矩阵Λ(ω)=diag[Λ1(ω),Λ2(ω)];I为2×2 阶的单位矩阵。由于存在Λi(-ω)=Λi(ω)以及ψi(-ω)=,因此可令

式中,i为虚数单位。根据文献[13],主余震向量过程J(t)的第r个分量过程Jr(t)的POD公式可表达为:
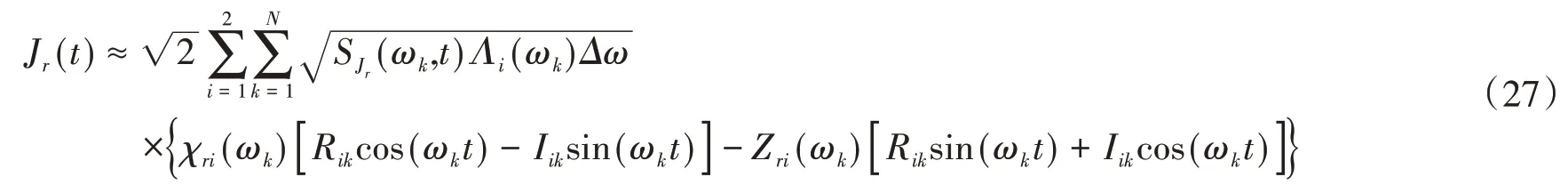
式中:N为频率截断项数;Δω为频率步长;ωk=kΔω(k=1,2,...,N);Rik和Iik为零均值的正交随机变量,满足如下基本条件:
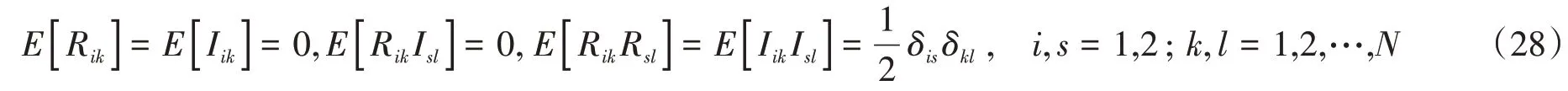
4.2 正交随机变量的降维表达
需要说明的是,随机向量过程模拟的POD 方法在本质上属于传统Monte Carlo 方法,然而,传统Monte Carlo方法通常需要进行大量的随机抽样才能达到令人满意的模拟精度,一方面,由于生成样本数量巨大,极大地增加了结构动力反应分析的计算量;另一方面,Monte Carlo 方法在本质上属于随机抽样方法,导致所生成的样本概率信息不完备,无法进行结构精细化动力反应分析和动力可靠性评价。为克服传统Monte Carlo方法的上述挑战,文中引入基于随机函数的降维思想,将正交随机变量{Rik,Iik}定义为如下的基本随机变量的函数形式[13]:
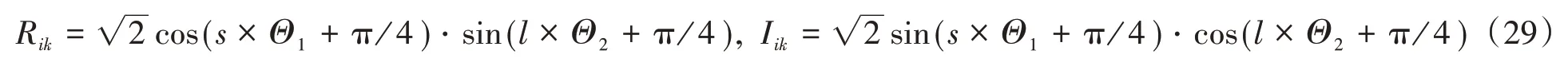
式中,i,s=1,2;k,l=1,2,…,N;Θi(i=1,2)为在区间(0,2π]上均匀分布且相互独立的基本随机变量。
显然,式(29)所定义的随机函数形式完全满足式(28)的基本条件。这样,通过降维模拟方法,实现了仅需2个基本随机变量即可精细化模拟主余震向量过程,且生成的代表性时程具有赋得概率,所有代表性时程集合构成一个完备的概率集,为与概率密度演化方法结合实现复杂结构精细化动力反应分析与动力可靠性评价奠定了基础。
5 模拟步骤及数值算例
5.1 模拟步骤
主余震向量过程的具体模拟步骤如下:
(1)确定相干函数矩阵γ(ω)。该矩阵的非对角元素根据第2节建议的主余震相干函数模型来计算。
(2)构造主余震型的演变功率谱模型。根据第3 节建议的参数取值,代入式(4)、式(5)和式(6)中,即可确定主余震型的演变功率谱模型。

(4)确定正交随机变量{Rik,Iik}。将上一步骤中生成的Θi(i=1,2)的代表性点集代入到式(29)中,此处,需要注意的是,为实现主余震向量过程的模拟,应进行确定性的映射变换(s,l)→(i,k)。这一确定性的一一映射过程可以通过MATLAB 工具箱中的rand(‘state’,0)和temp=randperm(2×N)函数实现。这样,即可唯一确定正交随机变量{Rik,Iik}。
(5)生成主余震型地震动的代表性时程。将主余震的相干函数矩阵γ(ω)、演变功率谱模型以及正交随机变量{Rik,Iik}代入到式(27)中,即可生成主余震型地震动的代表性时程,且每条代表性时程的赋得概率与初始代表性点的赋得概率相同,均为Pl。
5.2 数值算例
在本算例中,以II 类场地为例,参数取值为:主震模拟持时25 s,余震模拟持时20 s,时间步长0.01 s,截断频率,频率步长,代表性时程数量144,主震峰值加速度,主震峰值因子3,根据表6,余震峰值加速度,余震峰值因子2.75。其余参数按照表5取值。
图5为采用降维模拟方法生成的主余震向量过程模拟结果,其中,图5(a)为主余震向量过程的代表性时程,图5(b)和图5(c)分别为主余震向量过程的均值、标准差模拟值与目标值的比较结果。为进一步说明降维模拟方法的精确性,分别计算了144 和987 条代表性时程的均值与标准差误差,结果列于表7 中。从图5(a)可以看出,生成的代表性时程具有明显的主余震序列型地震动的特征,即主震和余震在持时、频谱以及幅值等方面都显示出明显的差异性。从图5(b)、图5(c)和表7 可以看出,主余震向量过程的均值和标准差均与对应的目标值拟合良好,其中均值误差为0,标准差误差随着代表性时程数量增多而减小,验证了降维模拟方法具有较好的收敛性。同时,在仅有144条代表性时程时标准差误差即小于5%,能够满足工程需求,验证了降维方法具有较好的精确性。
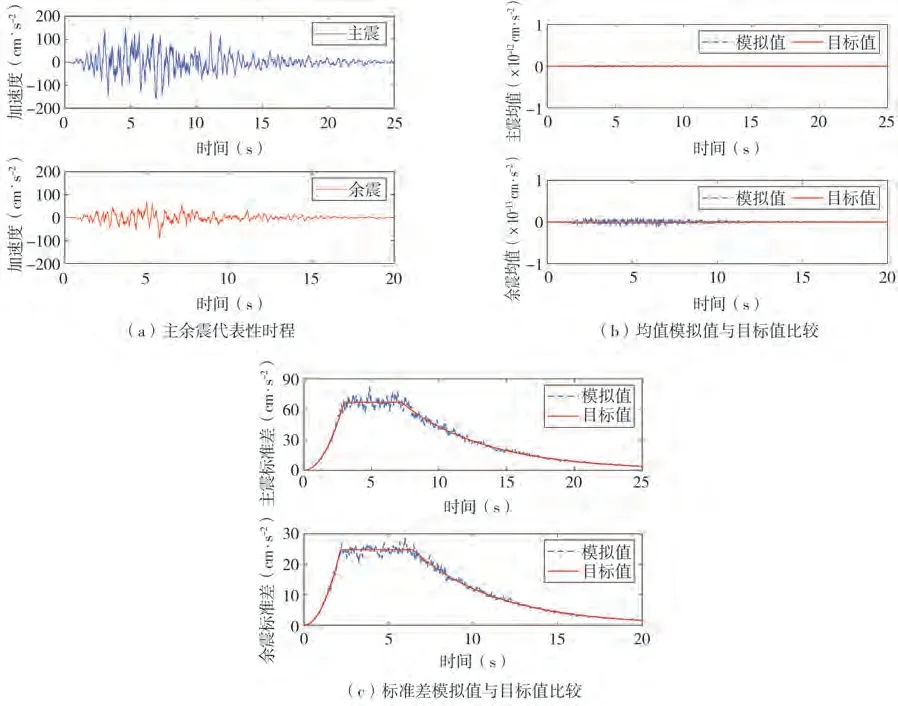
图5 II类场地主余震向量过程模拟结果Fig.5 Simulation results of main-aftershock vector process for site classification II

表7 主余震向量过程的模拟误差Table 7 Simulation error of main-aftershock vector process
图6(a)为Ⅰ1、Ⅱ、Ⅲ三类场地(144×3 组)代表性时程的主余震间相干性与488 组实测强震记录的对比结果;图6(b)及图6(c)为Ⅱ类场地144 组代表性时程的主余震反应谱模拟值与实测强震记录的对比结果。其中,对于反应谱,需要将主震实测记录调幅至200 cm/s2,余震实测记录调幅至60.61 cm/s2。
从图6 可以看出,主余震代表性时程间具有良好的相干性,且与实测记录拟合一致,证明了文中所建议的相干函数模型的正确性。同时,主震和余震的反应谱模拟值均与对应的实测记录拟合良好,验证了文中所提出的参数识别方法的有效性。
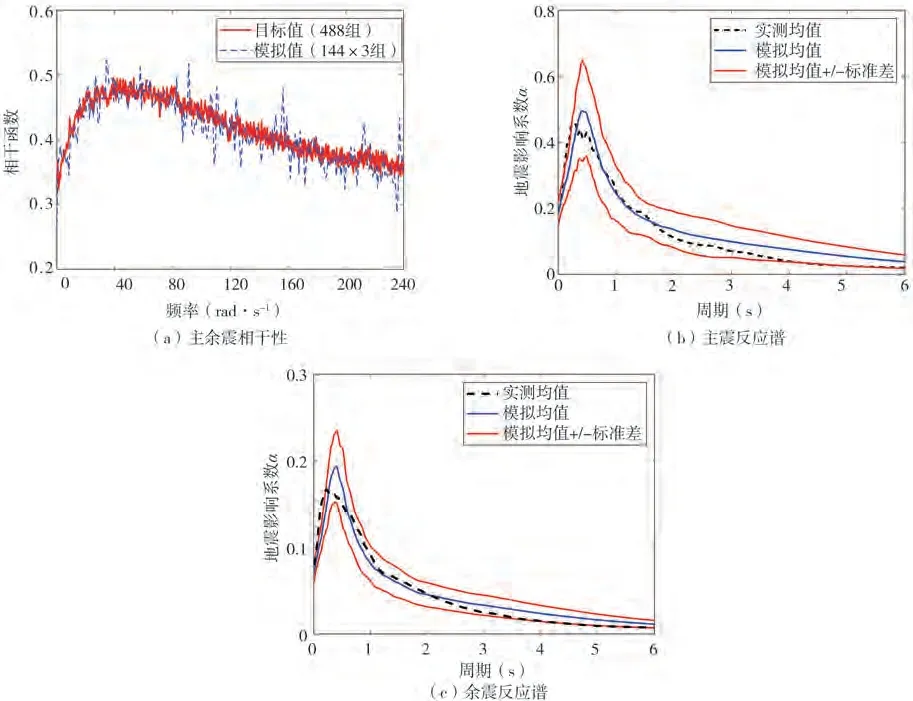
图6 主余震相干性和反应谱的模拟值与目标值比较Fig.6 Comparison of the simulated values and the corresponding target values of the coherence and response spectrum of the main-aftershocks
6 结论
文中从实测强震记录出发,对主余震间的相干性和演变功率谱模型的参数关系进行了系统分析,并通过引入随机函数思想,实现了基于POD方法的主余震向量过程降维模拟。文中得出的主要结论如下:
(1)实测强震记录显示出主余震间具有明显的相干性,且随着频率的增大相干性总体上呈现递减趋势。据此,文中建议了一种用于模拟主余震相干性的傅里叶级数模型,并通过与实测记录对比验证了该相干函数模型的有效性。
(2)文中对主余震的演变功率谱模型参数进行了识别,并给出了对应于I1、II、III类场地的主余震演变功率谱模型参数的建议取值。结果表明,相较于余震,主震的持时更长,能量更高,卓越频率更低。
(3)将主余震视作一个向量过程,实现了主余震序列型地震动的一体化高效模拟。通过该方法,可一次性生成主震与余震的代表性时程集合,而不必将主余震作为2个随机过程分别进行模拟,这样不仅体现了主余震间的相干性,同时可大幅提高计算效率。
(4)基于随机函数的降维方法仅需数百条代表性时程即可在全概率信息上反映主余震向量过程的概率特性,这为结合概率密度演化理论进行主余震作用下工程结构的精细化动力反应分析与可靠性评价奠定了基础。
致谢:感谢中国地震局工程力学研究所为本研究提供数据支持!

