地震动参数与既有RC框架校舍加固前后抗震性能指标相关性分析

杨连森，陈 鑫，谈丽华，孙 勇，刘 涛，还 毅

（1.苏州科技大学江苏省结构工程重点实验室，江苏苏州 215011；2.中衡设计集团股份有限公司，江苏苏州 215021；3.江苏省建筑科学研究院有限公司，江苏南京 210008；4.江苏省住房和城乡建设厅，江苏南京 210036；5 中央军委后勤保障部工程质量监督中心，北京1 000373）

引言

地震具有突发性强、破坏性大、成灾广泛以及防御难度较大等特点。它造成的直接人员伤亡和财产损失巨大，2019 年仅中国大陆地区就发生15 次地震灾害，造成17 人死亡，425 人受伤，直接经济损失约91 亿元［1］。更早之前的汶川地震受灾面积达到10万km2，69 227人死亡，17 923人失踪，375 783人受伤，直接经济损失达8 523亿元［2-3］。这些都威胁着人民生命财产安全，影响了社会经济发展。

目前，多层钢筋混凝土（Reinforced Concrete，RC）框架结构是我国中小学校舍中最常见的结构形式，但此类建筑较多存在着不满足现行抗震设防水准、超过设计使用年限、混凝土剥落或钢筋锈蚀等问题，有较大的安全隐患。而校舍建筑对保障学生生命安全、为震灾发生时提供重要应急避难场所等有着重要的意义。因此，有序对此类建筑开展性能提升显得尤为迫切［4］。

目前，针对钢筋混凝土框架结构，工程中常用的加固技术主要有：增大截面法、粘贴钢板法、外加预应力加固法、增设支点加固法和粘贴纤维法等［5］。相关的研究已经较为成熟，Chen Weihong 等［6］利用碳纤维增强聚合物（CFRP）加固非延性钢筋混凝土框架，通过2 个缩尺框架试验的对比发现：采用的加固方法能显著提升加固后混凝土框架的抗震性能。He Jianping等［7］通过粘弹性阻尼器对八层三跨框架加固前后不同位置的位移响应进行了比较，结果表明：设置粘弹性阻尼器能够较好地抑制结构的地震响应，降低结构地震损伤。周春利等［8］利用ABAQUS对采用外包钢板加固节点的混凝土框架进行分析，结果表明：加固后框架节点多个抗震性能指标均有一定程度提升。Hu Bo 等［9］通过对4 种不同加固方式加固的框架结构进行低周往复试验研究，对比试验结果发现：加固可以改变框架的破坏模式，加固后的结构刚度、承载能力等性能都显著提高。

近年来的研究发现，地震动参数对结构抗震性能有着较大的影响。Sang-Hoon Oh 等［10］考虑远断层长周期地震动，对建筑物的损伤分布模式进行了对比分析，研究表明：随着地震动卓越周期的增加，分析模型的损伤分布趋于较低楼层，随着建筑物自振周期的增加，损伤分布集中在较高楼层。郝建兵等［11］通过研究PGA、PGV等18 个地震动指标与残余变形之间的关系发现：不同指标与残余变形之间的相关系数受强度折减系数影响很大，基本不受屈服后刚度系数的影响。吴晓阳等［12］，以场地覆盖层厚度D、场地特征、周期T、场地Vs30以及场地等效剪切波速Vse为场地特征参数，研究放大系数FPGA与场地特征参数之间的相关性，结果表明FPGA与场地特征参数的相关性随地震动强度增大而增大。胡进军等［13］计算考虑场地类别和断层距参数的地震动和结构响应参数相关性时，结果表明在研究结构响应与地震动参数相关性时需要考虑场地条件与断层距的影响。Habibi等［14］对描述目标位移和地震动参数之间关系的相关系数进行了评估，结果表明，峰值加速度与目标位移相关性较差，而豪斯纳强度、谱伪加速度、谱伪速度和峰值地面速度与目标位移相关性较强。

上述研究可见，不同地震动参数对结构地震响应影响不同，其影响规律对结构与加固设计有着重要的指导作用。然而，当前该方面的研究多针对常规结构，对典型校舍及其加固后的抗震性能在不同地震动参数下的影响规律研究相对较少。为此，文中以某小学教学楼为对象，开展不同参数地震动作用下的既有RC框架校舍加固前后抗震性能的对比研究。首先，阐述反映地震动特性的关键指标，选取具有不同地震动特性的地震波；随后，介绍项目基本信息，并针对该RC框架校舍开展结构加固设计；进而，借助结构有限元模型，对比分析不同特性地震动作用下结构加固前后的地震响应；最后，对比分析加固前后结构薄弱层最大层间位移角、残余层间位移角等关键性能指标与地震动参数相关性，探讨地震动参数对该类抗震性能的影响规律。

1 地震动特性与选择

1.1 地震动参数

地震动是由震源释放出来的地震波引起的地面运动。它是由不同频率、不同幅值（或强度）的地面运动在一个有限时间范围内的集合，地震动参数是表征地震引起的地面运动的物理参数，包括峰值、有效峰值、反应谱和持续时间等。文中选取的参数有地震动的拟合特征周期、震中距、剪切波速（VS30）、峰值速度和峰值加速度的比值（PGV/PGA）。

地震动拟合特征周期Tg可按下式计算：

式中，有效峰值速度EPV=Sv/2.5，有效峰值加速度EPA=Sa/2.5，Sa取阻尼比为5%的加速度反应谱周期为0.1～0.5 s之间的平均值；Sv取阻尼比为5%的速度反应谱周期为0.5～2 s之间的平均值；常数2.5为0.05阻尼比加速度反应谱的平均放大系数［15］。

震中距指测站到地震中心的地球球面距离［16］，随着震中距的增加，地震的影响逐渐降低。

剪切波速VS30为地表上部土层30 m的平均剪切波速度，是目前强地震动预测方程中最普遍的场地参数，可以用来定义场地土类别［17］。

峰值速度和峰值加速度的比值（PGV/PGA）是用来甄别地震波有无脉冲的条件，当PGV/PGA＞0.2时，认为是脉冲型地震；当PGV/PGA＜0.2时认为是无脉冲型地震［18］。

1.2 地震动记录选取

近年来，近场地震对结构响应影响的研究广受关注，其较大的速度脉冲、较长的特征周期等特性通常会对结构产生较为严重的影响［19］。为此，文中在选择地震动记录时，充分考虑不同特性的地震动，分别选取了10条近场地震波和10条远场地震波。近场地震主要是指距离地震断层不超过20 km场地上的地面运动［20］，其地震动记录选取依据如下：（1）震级（Magnitude）6.5 级以上；（2）震中距小于15 km；（3）表层30 m 深度内的平均剪切波速度（VS30）变化范围为：260～510 m/s；（4）峰值加速度PGA大于200 cm/s2，并且峰值速度PGV大于40 cm/s；（5）有明显的速度脉冲，峰值速度PGV与峰值加速度PGA之比大于0.2。

基于上述原则，文中选取的20 条地震波的参数见表1，各条地震波动力系数曲线与设计反应谱对比如图1（a）所示，其中两条典型地震波的时程曲线如图1（b）所示。

表1 各条地震波参数及基底剪力Table 1 Seismic wave parameters and base shear force

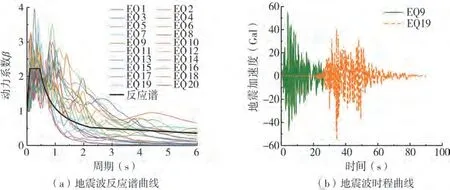
图1 时程分析地震波Fig.1 Time history analysis of seismic waves

2 既有RC框架校舍加固设计

2.1 工程概况

江都区实验小学建乐校区教学楼，位于扬州市江都区仙女镇乐和路1号，建于2006年，钢筋混凝土框架结构，主体3层，局部4层突出屋面，建筑总高度13.75 m。该建筑原为丙类建筑，结构的安全等级和耐火等级均为二级，设计地震分组为第1 组，抗震设防烈度7 度，设计基本加速度0.15 g。框架抗震等级三级，建筑场地类别为Ⅲ类，场地特征周期为0.55 s，结构的阻尼比为0.05。结构平面布置如图2所示，结构平面设有结构缝，分析时可将结构分割为4个单体进行分析，文中选取其中单体A（⑥-⑧轴）的典型结构进行分析。该区域结构首层层高为4.2 m，2、3 层层高均为3.6 m。结构横向两跨，跨度分别为3.0 m 和7.2 m，为典型的教室、阳台两跨RC框架校舍结构，具有较好的代表性。

图2 结构总平面图Fig.2 Structure master plan

2.2 结构加固设计

根据结构安全鉴定结果，该建筑存在以下问题：（1）建筑的抗震构造措施不满足现行规范要求；（2）部分钢筋混凝土构件承载力不满足要求；因此，须对该结构进行结构加固。加固后，建筑结构的安全等级为二级，根据碳纤维布、胶粘剂的使用年限和《建筑抗震鉴定标准》（GB50023-2009）等，综合计算确定结构设计使用年限为40年（40年后须进行可靠性鉴定，合格后可继续使用），建筑抗震设防类别提升为重点设防建筑（乙类）。

根据结构现状和结构鉴定报告等，优先对所有柱子采用外包角钢法加固，计算发现角钢加固后大部分柱子承载力仍无法满足要求，结合计算结果，最终提出结构加固方案如图3和4所示。

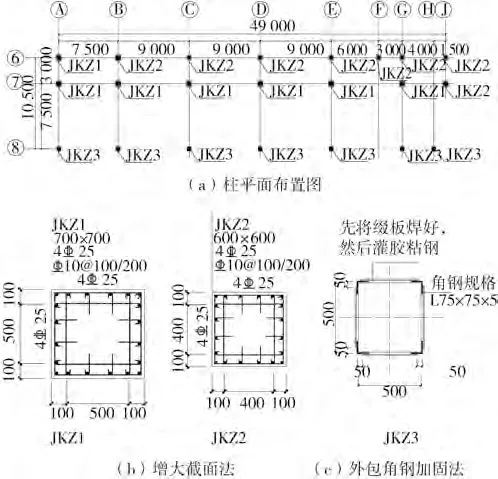
图3 框架柱加固方法Fig.3 Frame column reinforcement method

（1）⑥、⑦号轴线上的1-3层柱均使用增大截面法（JKZ1、JKZ2）进行加固，⑧号轴线上的1-3层柱均使用外包钢法加固（JKZ3）。JKZ1截面由500 mm×500 mm增大至700 mm×700 mm，每边增大100 mm，增大部分截面配筋为，新增部分箍筋为。JKZ2 由400 mm×400 mm 增大为600 mm×600 mm，四面都增100 mm，截面配筋为，新增柱箍筋为。新增截面采用灌浆料浇筑，等效强度为C30。JKZ3 加固角钢采用L75×75×5，柱高方向设置40×4 缀板，加密区间距200 mm，非加密区间距300 mm。将角钢布置在柱子的4个角点，然后与缀板焊接，焊好后灌注环氧树脂进行粘结。

（2）所有的框架梁均在梁底部通长粘贴200 mm宽的200 g碳纤维布来提高梁的抗弯承载力和延性。

图4 框架梁加固方法Fig.4 Frame beam reinforcement method

3 既有多层RC框架校舍抗震性能分析

3.1 结构分析模型

分别利用结构设计软件PKPM、结构分析软件Etabs 和OpenSees 建立结构分析模型，其中Etabs 模型和OpenSees模型如图5所示。前两者为结构弹性分析模型，后者为结构弹塑性分析模型。Etabs模型中仅考虑钢和混凝土材料的弹性特性，梁、柱采用框架单元，楼板采用壳单元，结构底部固接。OpenSees 模型中采用的材料本构与构件单元介绍如下。

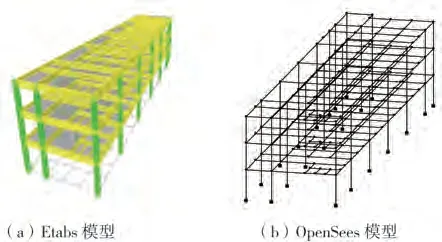
图5 结构有限元模型Fig.5 Structural finite element model

（1）材料特性及弹塑性本构

加固方案中，原结构部分采用C25 混凝土及HRB400 钢筋，增大截面部分采用C30 灌浆料及HRB400钢筋。建模时，保护层部分混凝土材料均采用Concrete02 本构模型（图6（a）），Concrete02 基于Kent-Park模型，不考虑箍筋的约束作用；核心区混凝土采用Concrete04 本构模型（图6（b）），考虑箍筋约束作用；钢筋和钢板均采用Steel01 本构模型（图6（c）），Steel01采用了理想弹塑性模型；碳纤维采用弹性模量为2.4×105MPa 的普通弹性材料模拟。

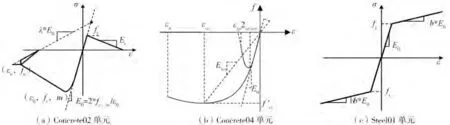
图6 材料应力-应变关系Fig.6 Material stress-strain relationship

（2）构件单元选择

OpenSees中常用的纤维单元有2种：一种是基于位移的梁单元（dispBeamColumn）；另一种是基于力的梁单元（nonlinearBeamColumn）。dispBeamColumn 的原理是刚度法，以位移作为基本未知量，通过构造刚度矩阵和力矩阵来求解位移，再由节点位移计算其他未知量。nonlinearBeamColumn 的原理是柔度法，以力作为基本未知量，通过构造柔度矩阵和位移矩阵求解力，再计算其他未知量。文中采用nonlinearBeamColumn 模拟考虑塑性的梁、柱构件。

（3）截面纤维模型的划分

梁、柱构件纤维划分的基本原理是在构件截面上双向纤维划分，同时可沿纵向将构件划分多个单元或者设置多个积分点。柱加大截面加固前后的纤维分布如图7（a）所示，柱角钢加固前后的纤维划分如图7（b）所示，梁粘贴碳纤维加固前后的纤维分布如图7（c）所示。

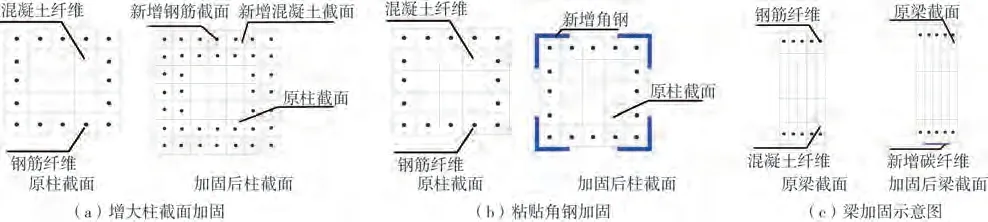
图7 截面纤维划分Fig.7 Sectional fiber division

3.2 结构动力特性分析

利用上述3个分析模型分别对结构进行动力特性分析，得到加固前、后结构前3 阶自振周期（表2）和前3 阶振型（图8）。对比可见：（1）3个模型得到的结构前3阶自振周期较为接近，1 阶周期平均仅相差0.32%，3 阶周期相差最大仅为4.5%，采用不同软件所建立模型的动力特性相近，模型具有较高的可靠性，可用于进一步的结构性能分析；（2）加固后，增大截面和外包角钢等措施使得结构整体刚度增加，前3阶自振周期分别减小35.6%、33.9%和37.9%；（3）结构1 阶振型为横向平动，2 阶振型为纵向平动，3 阶振型为扭转，呈现典型的多层框架自振特性。

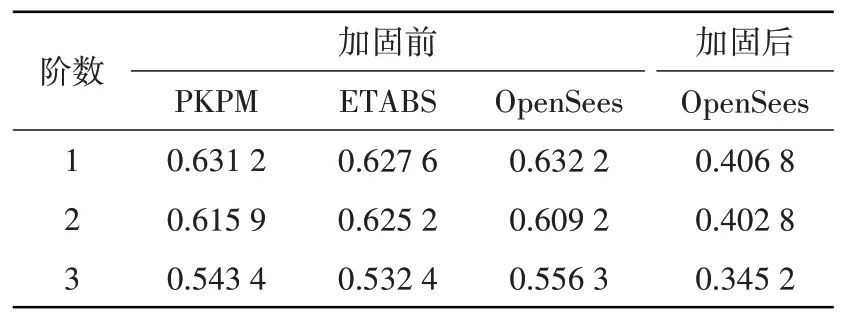
表2 加固前后结构前3阶自振周期Table 2 The first three periods of the structure before and after reinforcement

图8 前3阶模态振型图Fig.8 Vibration shape diagram of the first 3 models

3.3 多遇地震作用下结构响应

图9 给出了多遇地震作用下结构层间位移角，对比可见：（1）多遇地震作用下，结构的最大层间位移角出现在底层，远场地震和近场地震作用下的平均值分别为1/909 和1/833；（2）加固后，远场和近场地震作用下结构最大层间位移角的平均值分别均为1/1470，相对于加固前分别降低39.94%和40.80%，同时2 层和3 层层间位移角均有不同程度的降低；（3）由于对柱沿高度采用了相同的加固策略，结构加固并未改变结构层间位移角的分布规律；（4）由图9（c）可见，加固前后结构底层均未进入塑性，加固后曲线斜率大于加固前，结构刚度增加，层间位移减小，同时由于结构周期的降低，导致地震作用增大，基底反力略有增加。

图9 多遇地震作用下的结构位移响应Fig.9 Structural displacement response under frequent earthquakes

3.4 罕遇地震作用下结构响应

图10为罕遇地震作用下结构层间位移角。分析可见：（1）无论远场地震还是近场地震作用下，结构的底层位移角均有部分工况超过规范的限值，远场地震和近场地震作用下的底层层间位移角最大分别可达1/30和1/13，近场地震作用下的平均值为1/29，大于远场地震作用下的平均值1/50；（2）加固后，远场地震和近场地震层间位移角平均值为1/111和1/84，相对于加固前分别降低73.05%和84.55%；（3）加固前结构底层较大程度地进入塑性，而2、3层进入塑性程度相对较小，因此加固后的层间位移角降低效果小于底层；（4）相对于多遇地震，结构底层进入塑性程度较高，层刚度有较大程度的退化，加固后，结构底层进入塑性程度显著降低，但由于楼层侧向承载能力的提高，基底剪力增加。

图10 罕遇地震作用下的结构位移响应Fig.10 Structural displacement response under rare earthquakes

图11为罕遇地震作用下结构顶点位移时程响应，由图可知：（1）加固后，结构顶点位移有一定的衰减，在EQ9和EQ19波作用下，结构顶点位移分别降低47.83%和34.15%；（2）由于加固前结构整体刚度有较大程度的退化，而加固后结构整体刚度退化较小，因此相同地震波作用下，结构顶点位移时程具有一定的相位差，且顶点峰值位移不在同一时刻；（3）EQ9波作用下，加固前结构残余变形较大，达1/108，加固后结构顶点残余位移仅为1/417 mm，降低97.3%，结构可恢复性能显著改善。

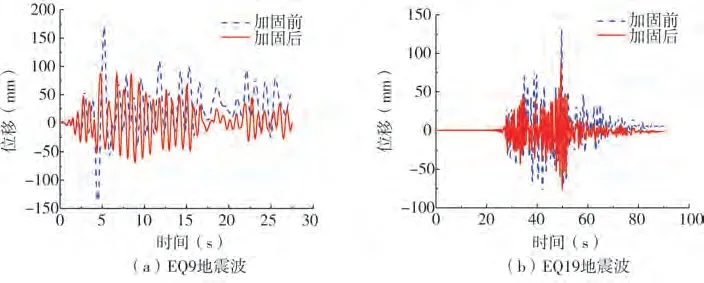
图11 罕遇地震下的结构顶点位移曲线Fig.11 Displacement curve of structure vertex under rare earthquake

4 地震动参数与结构抗震性能指标相关性分析

文中以层间位移角和残余层间位移角为指标对相关性进行分析，加固方案和加固方式对层间位移角和残余层间位移角有直接影响，进而影响与地震动参数的相关性。而文中采用加固方案是目前钢筋混凝土框架结构加固时最常规且使用最多的加固方案，研究成果对RC框架抗震性能评估和加固设计具有一定的参考意义。

4.1 相关性指标定义

为分析地震动参数对结构地震响应以及加固效果的影响，引入相关系数作为地震动参数与结构抗震性能指标相关性的评价指标。由于研究对象的不同，相关系数有多种定义方式，较为常用的是皮尔逊相关系数，其计算公式如下：

式中：X和Y为自变量；Cov（X，Y）为X与Y的协方差；Var［X］和Var［Y］分别为X和Y的方差。

4.2 地震动参数与薄弱层层间位移角相关性分析

利用式（2）分析表1中20条地震波作用下地震动参数和薄弱层层间位移角之间的相关系数，结果如表3所示，其分布关系见图12。对比可见：（1）除震中距与远/近场地震负相关外，表1 选择的其余地震动参数分布相对较为均匀，具有较好的代表性；（2）总体上，结构薄弱层层间位移角随着拟合特征周期、平均剪切波速和PGV/PGA数值的增大而增大、震中距的增大而减小；（3）结构薄弱层层间位移角与拟合特征周期和PGV/PGA相关性较大，与震中距和平均剪切波速VS30的相关性较小，加固后相关性有一定程度降低；（4）加固后的薄弱层层间位移角降低率同样与拟合特征周期和PGV/PGA相关性较大，但与各参数的相关系数有一定程度降低，且与剪切波速的相关系数降低达98.4%。

表3 地震动参数和薄弱层层间位移角相关系数Table 3 Correlation coefficients of ground motion parameters and displacement angles between weak layers

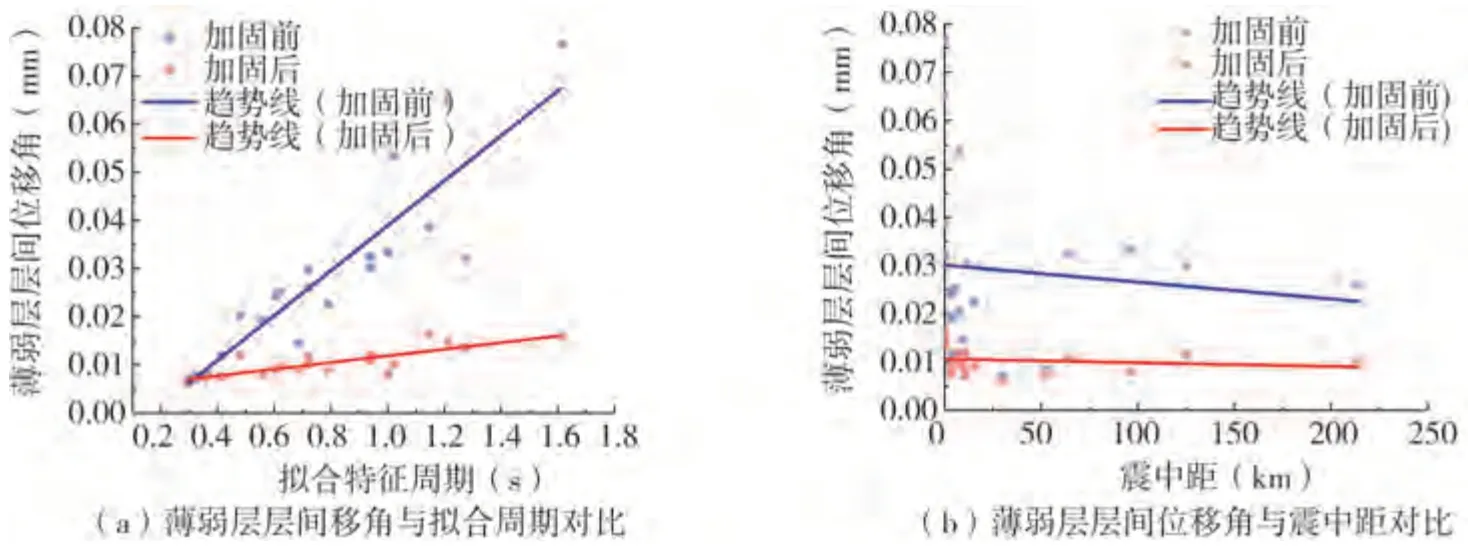
图12 地震波参数和薄弱层层间位移角的对比Fig.12 Comparison of seismic wave parameters and the displacement angle between weak layers

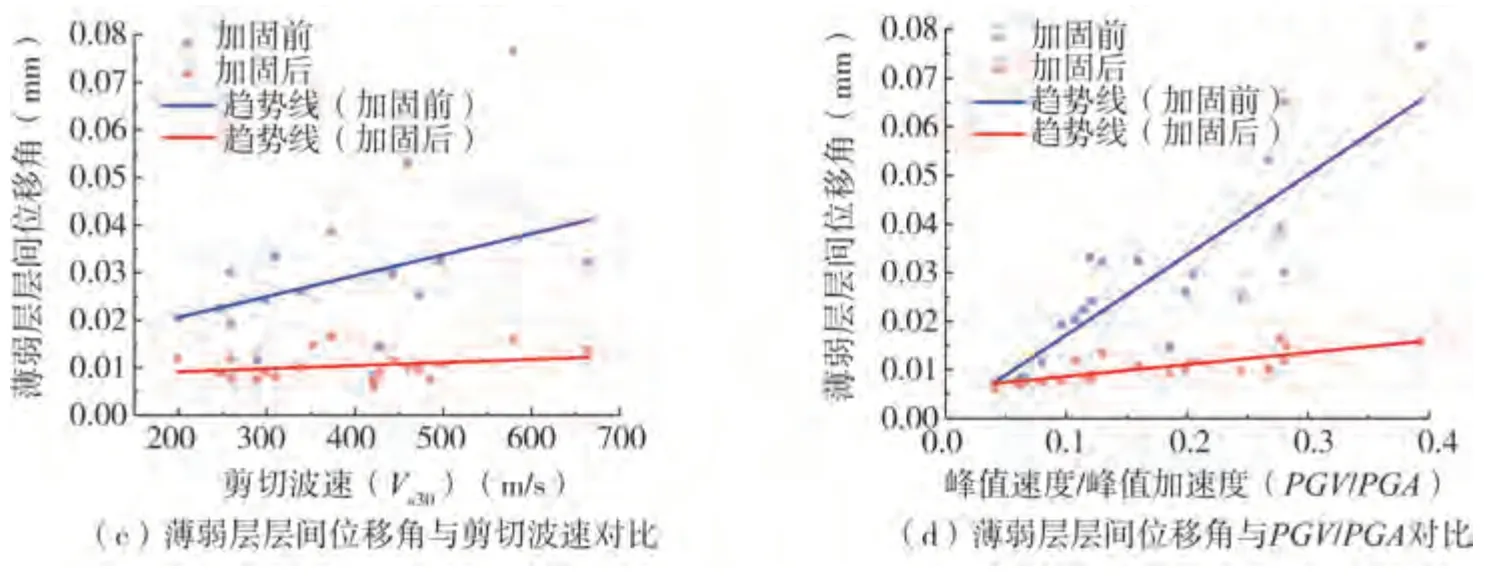
图12（续）Fig.12 （Continued）

4.3 地震动参数与薄弱层残余层间位移角相关性分析

地震动参数和薄弱层残余层间位移角之间的相关系数见表4，其分布关系见图13，分析可见：（1）结构薄弱层残余层间位移角与拟合特征周期和PGV/PGA相关性较大，与震中距和平均剪切波速VS30的相关性较小，但其相关系数总体小于地震动参数和薄弱层层间位移角的相关系数，且加固后，相关系数同样有较大降低；（2）结构残余层间位移角随着拟合特征周期、平均剪切波速、PGV/PGA数值的增大而增大、震中距的增大而减小；（3）残余层间位移角降低率同样与拟合特征周期和PGV/PGA相关性较大，相关系数数值与加固后相关系数相对接近。

表4 地震动参数与残余层间位移角相关系数Table 4 Correlation coefficients of ground motion parameters and residual interlayer displacement angle

图13 地震波参数和残余层间位移角的对比Fig.13 Comparison of seismic wave parameters and residual interlayer displacement angle

5 结论

文中开展了中小学校舍常用的典型多层RC 框架结构的加固设计与抗震性能分析，重点分析了不同地震动参数与结构抗震性能指标的相关性，结果表明：

（1）针对多层教学楼的加固设计，有效的提高了结构的抗震性能，多遇地震作用下，结构底层层间位移角平均衰减40.37%；罕遇地震下，结构底层层间位移角平均衰减64.03%，残余层间位移角平均衰减92.05%。

（2）由于速度脉冲等特性的影响，近场地震作用下，结构响应大于远场地震作用下，多遇和罕遇地震作用下近场地震工况的底层层间位移角平均值分别为远场地震工况的1.02和1.90倍。

（3）拟合特征周期、震中距、平均剪切波速和PGV/PGA4 个地震动参数与结构薄弱层层间位移角的相关系数分别为0.897 5、-0.110 4、0.285 9 和0.849 2，与结构薄弱层残余层间位移角的相关系数分别为0.846 6、-0.260 2、0.299 9和0.782 9，可见拟合特征周期和PGV/PGA对结构抗震性能指标影响较大，随着这两个参数的增加，结构地震响应均随之增大。

（4）加固后，结构薄弱层层间位移角和残余层间位移角与地震动参数的相关系数均有不同程度的降低，其中残余层间位移角的相关系数降低更大。