基于叠合空腔楼板的PTRMD系统随机动力性能及振动台试验研究

孙 磊，李书进，黄丽珍

（1.湖北工程学院土木工程学院，湖北孝感 432000；2.武汉理工大学土木工程与建筑学院，湖北武汉 430070）

引言

得益于高度工业化的生产模式以及良好的保温隔热性能，预制叠合空腔楼板被广泛应用于各类装配式建筑结构，而利用装配式构件进行合理的阻尼器设置这一思路也受到了大量学者关注［1-3］。李书进等［4］以统计线性化方法分析了TRMD（Tuned Rotary Mass Damper）装置对空腔结构在确定性激励和随机激励作用下的振动控制效果，并且利用空腔特点有选择性的放入多个滚动小球，以MTRMD 代替单个TRMD 的方式，使控制系统更能满足地震激励的宽频特性。李书进等［5］对这种基于空腔楼板结构的TRMD系统进行了参数优化工作，运用定点理论得出系统最优参数，最后以蒙特卡洛模拟对比分析了最优参数TRMD 系统与普通参数TRMD系统的结构动力响应控制结果。

TRMD 装置较为单一的耗能机制限制了减振效率及其应用范围，碰撞耗能机制的引入为这种空腔阻尼器设计提供了新的方向。PMD（Pounding Mass Damper）装置应用于建筑结构方的研究已经从理论和试验2个方面展开了大量的研究，理论方面已经由Lieber［6］，Grubin［7］，Masri［8-11］等建立的塑性冲击模型转变为由Jankowski［12］提出的粘弹性碰撞模型，大量学者在这种粘弹性模型的基础上提出了适用于不同类型建筑结构振动控制的碰撞调谐阻尼器。SONG等［13］针对信号杆、转换塔以及海底油管设计了一种粘弹性碰撞阻尼器，并且取得了良好的减震效果［13］。

以这2 种较为成熟的振动控制装置为基础设计出的PTRMD（Pounding Tuned Rotary Mass Damper）装置，已经从理论和试验2个方面获得了该装置的减振性能研究结果并发表在文中作者的另外一篇论文中［14］。文中在此基础之上以一个6层框架结构作为受控结构，通过蒙特卡洛模拟得到了多自由度PTRMD受控结构在随机激励下的动力响应结果。将框架结构层间位移角作为可靠度计算标准，根据模拟得到的各层随机动力响应结果结合可靠度计算公式，计算得到框架结构在未受控和PTRMD 控制作用下可靠度对比结果。试验方面，进行了碰撞间距、质量比和激励频率这些关键参数分析，结合幅值和标准差减振率，验证前期数值模拟结果的同时总结出了各参数影响规律。文中的研究成果可为装配式耗能楼板的研发和抗震性能研究提供重要参考。

1 PTRMD动力学模型

1.1 PTRMD系统基本介绍

叠合空腔楼板以预制空腔构件拼接安装结合现场整体现浇的模式，实现装配式建造过程，楼板具体构造如图1（a）所示。为了更有效的利用空腔构件内部空间，设计了弧形的空腔底板和限位挡板，利用楼板振动过程中振子小球的滚动和碰撞效应实现耗能减振，空腔模块内部构造如图1（b）所示。

图1 叠合楼板及空腔模块内部构造示意图Fig.1 Structure diagram of composite floor slab and cavity mold block

PTRMD系统从功能上分为滚动调谐阻尼器和碰撞阻尼器两部分，整个装置包括：弧形轨道、滚动质量小球、设置于轨道上的限位挡板以及粘贴在挡板表面的粘弹性阻尼材料，装置具体构造见图2。通过调节限位挡板位置、小球质量及半径可以达到改变装置控制频率的目的，以满足不同受控结构的需要。

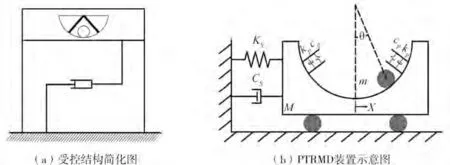
图2 PTRMD受控体系简化图Fig.2 Schematic diagram of PTRMD

1.2 PTRMD系统运动方程

PTRMD 系统运动方程的具体推导过程可参考文献［15］运动方程中会涉及到的变量和参数为：PTRMD装置中小球的质量m，受控结构的质量、刚度和阻尼，分别表示为Ms、Ks和Cs；运动过程中受控结构位移为xs，小球相对圆弧形轨道圆形的滚动角度为θ，轨道半径为R和小球半径为r，ρ=R-r，μ为轨道摩擦系数。

整个运动方程分为2个部分：

（1）小球自由振动阶段（|θ|≤θm，θm为粘弹性限位装置与小球碰撞时的小球运动角度），摩擦是PTRMD系统的主要耗能形式，运动方程的矩阵形式为：

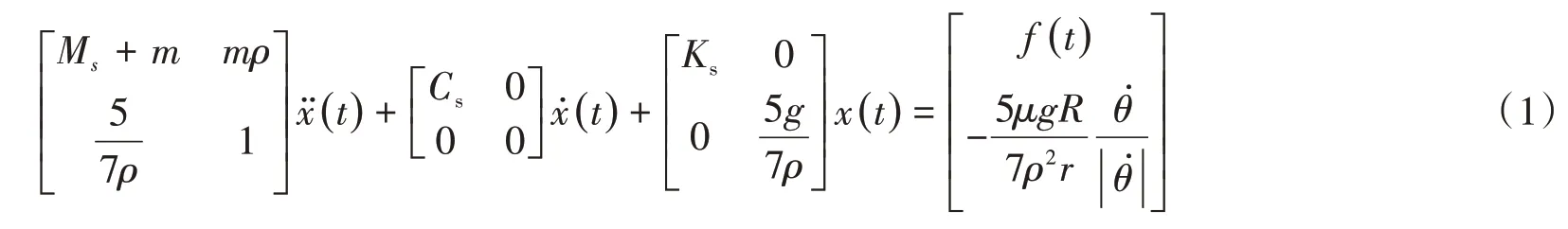
（2）小球与粘弹性缓冲材料碰撞阶段（|θ|＞θm），系统耗能方式将会从摩擦耗能转变成碰撞力耗能，得到碰撞阶段的运动微分方程：

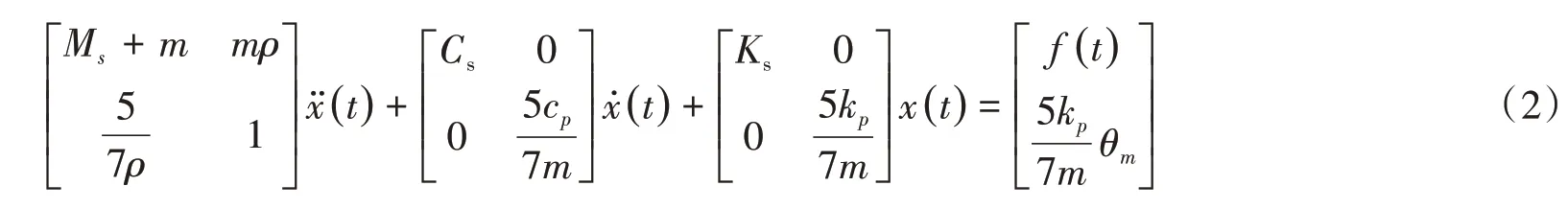
式中：kp和cp分别为求得的等效碰撞刚度和阻尼。

2 PTRMD受控结构随机动力响应结果

2.1 高斯随机过程模型

理想白噪声模型的特点是具有均匀分布的功率谱密度且符合高斯过程，在白噪声模型的基础上，通过改变双边功率谱密度的取值可实现Kanai-Tajimi 模型，以坚硬地表土层作为研究对象，其对应的ωg=5π、ζg=0.63［16］，代入到式（3），可计算得到，图3为生成的Kanai-Tajimi样本曲线。

图3 模拟得到的Kanai-Tajimi样本Fig.3 Kanai-Tajimi samples

2.2 多自由度PTRMD受控结构随机动力响应结果

为了研究PTRMD 系统的随机振动控制效果，本小节以一个6层框架结构为计算对象，将PTRMD 装置设置在结构顶层，具体模型简图如图4所示，地震动随机模型采用Kanai-Tajimi模型，考虑到进行可靠度分析的样本精度要求，蒙特卡洛模拟的样本数量为5 000，每条样本取点个数为1 024。只考虑一阶和二阶振型质量。首先通过计算得到结构的一阶自振频率为ω1=9.149 3 rad/s，二阶自振频率为ω2=26.913 6 rad/s，受控主结构质量为每层16 315 kg，一共6 层，结构层间刚度为23.5×103kN/m，在质量和刚度确定的情况下由结构一阶和二阶频率可算得主结构阻尼矩阵，小球与主结构的质量比设置为0.02，算的小球质量为1 957.8 kg，主结构和PTRMD装置具体参数见表1。

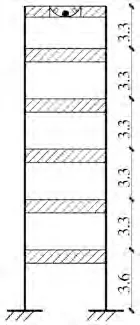
图4 6层多自由度PTRMD受控结构简化图（单位：m）Fig.4 Simplified diagram of six-layer structure controlled by PTRMD（Unit：m）

表1 受控结构和PTRMD装置参数表Table 1 Parameters for the PTRMD model

计算得到PTRMD 受控结构顶层位移响应标准差、层间位移响应标准差和减振率，分别列于图5 至图8。通过对比六层多自由度结构顶层的位移标准差，可发现在0～2 s 的时间段3 条位移标准差曲线几乎重合差异并不明显，在1.8 s 附近PTRMD 受控结构位移标准差开始趋于稳定，并在2 s 后保持在0.006 m 附近，未受控结构则持续上升一直到6 s时才开始趋于稳定最终稳定在0.009 m附近，从这一结果可看出PTRMD对受控结构在随机激励下的动力响应控制效果非常明显。图6可看出未受控结构的每层位移方差最大值是远大于PTRMD 受控结构，并且随着层高增加差距越大。图7 反应的是结构层间位移方差最大值对比，整体发展趋势是低楼层层间位移更大，随着楼层的增加层间位移不断减小，符合楼层位移的发展规律，未受控结构的层间位移方差最大值是远大于PTRMD 受控结构。图8中结构各层层间位移峰值减振率、中值减振率与均值减振率数值表现都较优秀，特别是第4 层峰值减振率达到64.24%；第6 层为结构顶层位移减震率，其均值也达到12.57%。从以上结果可分析得到，PTRMD系统对结构随机动力响应的控制效果是十分有效的。

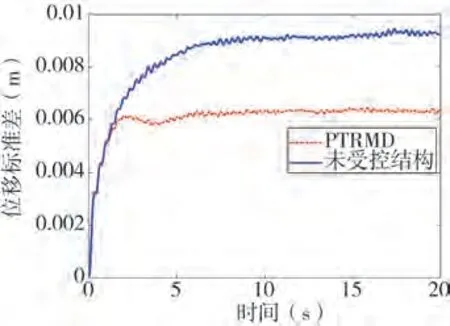
图5 受控结构顶层位移标准差Fig.5 Displacement standard deviation

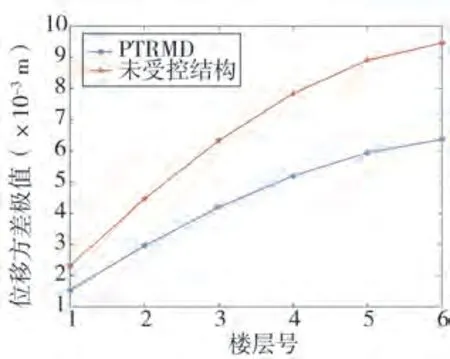
图6 受控结构不同楼层位移方差最大值Fig.6 The maximum displacement variance

图7 受控结构层间位移方差最大值Fig.7 The maximum variance of interlayer displacement

图8 减震率柱状图Fig.8 Shock absorption rate histogram

更详细的计算结果列于表2中，包括受控和未受控结构各层层间位移以及结构顶层位移的峰值、中值和均值。数值结果对比也可看出PTRMD受控结构各类型位移响应均小于未受控结构。

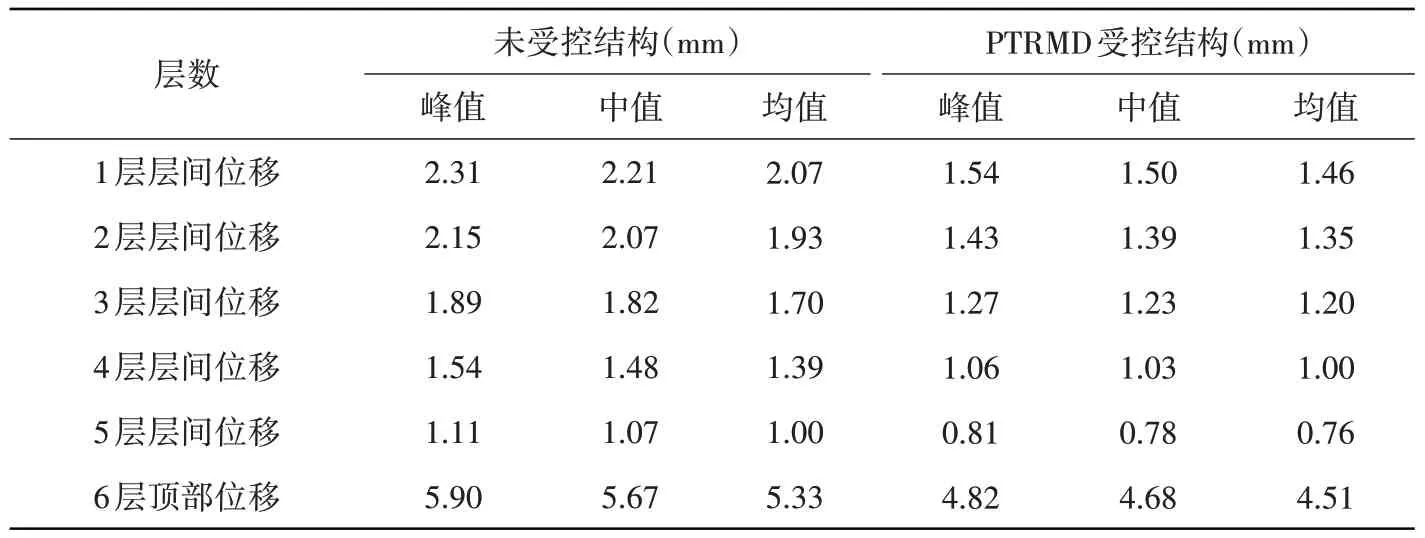
表2 不同楼层位移响应结果对比Table 2 Comparison of displacement response results of different floors

3 随机地震动作用下的整体抗震可靠度分析

为了更深入的研究PTRMD 对结构性能产生的影响，选取蒙特卡洛方法对PTRMD 系统和未受控结构的可靠度进行分析［17-19］。根据文中研究的振动控制装置的适用背景，以框架结构的层间位移作为结构整体可靠度的判别标准，由受控结构在随机激励作用下的动力响应结果，求得各层层间位移标准差，结合给定的楼层各层层高可得到层间位移角响应标准差，设为σθ，根据文献［20］中可靠度计算公式：

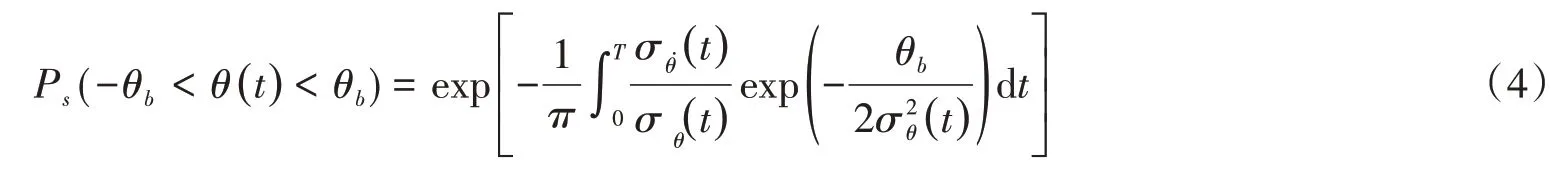
式中：θb为框架结构不同破坏要求下的层间位移角限制标准，而结构失效概率则可写为：

框架结构层间位移角根据设防水准的不同其极限值也有所不同，我们参考RC 框架结构的可靠度标准设置，表3［20］中列出了RC 框架结构设防水准为完好、轻微破坏、中等破坏和严重破坏等5个不同状态时的层间位移角极限值，选择轻微破坏时的层间位移角极限值作为可靠度和失效概率的计算标准。进行随机动力分析的PTRMD 系统各项参数参考表1，将样本数量为5 000 和样本取点个数为1 024 的Kanai-Tajimi 谱作用于受控结构得到随机动力响应结果，计算得到层间位移标准差并将标准差曲线列于图9～图10。

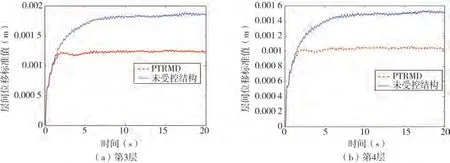
图9 层间位移标准差Fig.9 The standard deviation of story-drift

图10 层间位移标准差Fig.10 The standard deviation of story-drift

表3 RC框架结构层间位移角限制标准Table 3 Limit standard for story-drift of RC frame structure

观察层间位移响应标准差曲线图可发现，层间位移标准差最大值随着楼层的增加逐渐减小，以轻微破坏设防标准的层间位移角极限值作为标准，将各个曲线中的数据代入到式（4）和式（5）进行计算，可得到各层的可靠度和失效概率，将得到的失效概率结果列于表4。

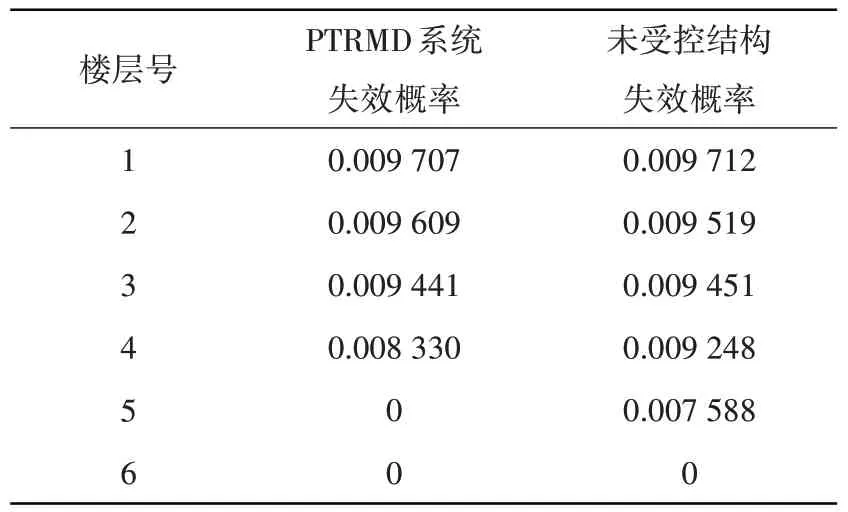
表4 结构层间位移失效概率Table 4 Failure probability of story-drift

分析表中的数据可看出，第1 层未受控结构失效概率比PTRMD 受控结构高0.5×10-5，而第2 层结构则从数据上表现出未受控失效概率低于受控结构的情况，差值达到0.9×10-4。从第3 层开始受控结构失效概率均要小于未受控结构，且差值呈增大趋势，第4层差值达到0.918×10-3，最后到第5层受控结构失效概率为0。

4 试验验证

4.1 试验模型及试验工况

试验的目的是为了在理论分析结果的基础上进一步验证PTRMD 装置的有效性，在对该装置的前期研究成果中已发现碰撞间距、质量比的设置以及外部激励频率对PTRMD 的减振性能影响较大［21］，故整个试验工况设置分为以下4个方面：（1）PTRMD模型与PMD模型对比；（2）不同碰撞间距PTRMD模型对比；（3）不同质量比PTRMD模型对比；（4）不同频率激励作用下PTRMD模型对比。

试验所使用的振动台仪器具体参数及各模型基本参数见表5，PMD 模型、PTRMD 模型及缩尺比例框架结构模型外观如图11所示。分别选取简谐波和地震波作为试验激励，其中地震波包括Cape波、El Centro波、Kobe波和North波，具体参数见表6。

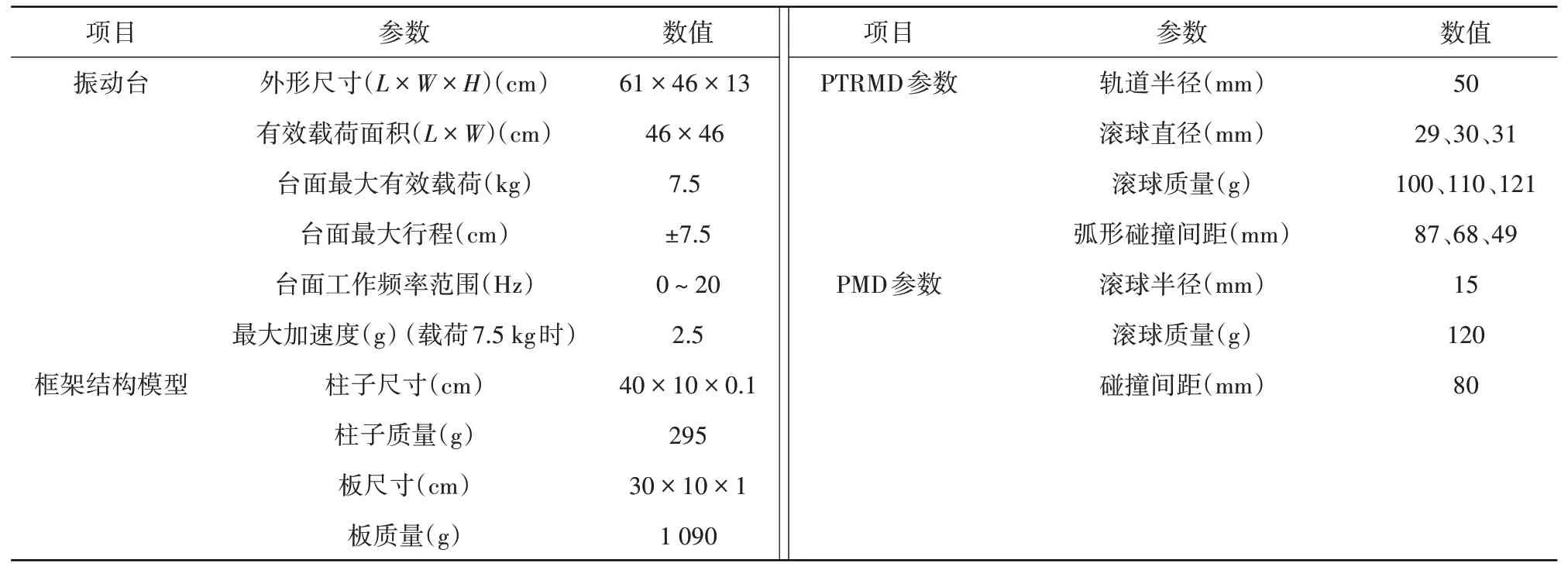
表5 试验仪器及模型参数Table 5 Instrumental and model parameters

表6 地震波特性Table 6 The characteristics of each seismic wave

图11 PMD模型、PTRMD模型及缩尺框架结构模型Fig.11 PMD，PTRMD and frame structure

4.2 试验结果

为了从试验数据中分析出准确的信息，根据工况及参数整理了以下试验结果，见图12：

图12 振动台试验结果Fig.12 Results of the shake table tests

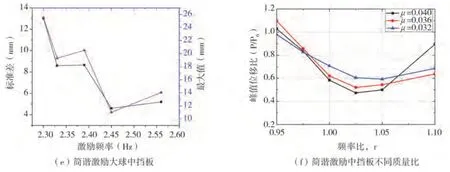
图12（续）Fig.12 （Continued）

（1）图12（a）～（d）为4种不同地震波作用下，不同碰撞间距PTRMD 及平底的PMD 控制下的主结构位移标准差减震率和峰值位移减震率。

首先，可观察到标准差减震率并不是始终大于峰值减震率，Cape 波、El Centro 波和North 波工况下标准差减震率最大值均可达到0.45 以上，峰值减震率基本在0.03 以下；Kobe 波则表现出峰值减震率反而大于标准差减震率，其峰值减震率在0.025～0.3范围内，标准差减震率在-0.04～0.08范围。

其次，碰撞间距对PTRMD 减震效果的影响的确十分明显，但规律并不固定。Cape波和El Centro 波的峰值减震率最大值均出现在间距49 mm 时，Cape 波达到0.028；Kobe 波和North 波则在间距87 mm 时峰值减震率表现最好，Kobe波达到0.3，North波达到0.26。

最后，对比平底的PMD 减震率发现，除了El Centro 波作用下出现68mm 碰撞间距的PTRMD 峰值减震率低于PMD，其他工况下PTRMD 模型的峰值减震率均优于PMD 模型。标准差减震率表现则有所差异，除El Centro 出现PMD 减震率最低的情况外，其他3 种波作用下，PMD 标准差减震率都较为优秀。

（2）简谐波激励下挡板间距设置为68 mm，图12（e）～（f）分别表现了激励频率变化影响效果及频率比与质量比耦合影响效应。首先，图12（e）可看出位移标准差与位移峰值变化趋势一致，这一点符合简谐激励特点；而激励频率对受控结构位移影响明显，最小位移出现在2.45 Hz，最大位移出现在2.30 Hz，差距达9 mm。

图12（f）进一步得到了3 种不同质量比μ（小球质量/主结构质量）PTRMD 模型峰值位移比，P为带PTRMD 模型主结构峰值位移，P0为未受控主结构峰值位移。在频率比1.0～1.05 范围，3 条曲线均满足质量比越大位移比越大，即减振效果越明显；与此同时，3 条曲线的最小值也都出现在频率比1.025 位置处，说明PTRMD 也具备调谐阻尼器的共振耗能最优特点；最后，可发现图12（f）中μ=0.032时曲线发展较为平缓，说明质量比较小时虽然无法获得最优的减振效果，但其对频率的敏感度降低鲁棒性得到提升。

5 结论

文中采用蒙特卡洛方法，研究了多自由度PTRMD 受控结构的随机动力响应结果，并根据振动台试验结果得到了，不同地震波激励作用下碰撞间距对减震率影响过程以及简谐波激励作用下频率和质量比等参数于减振率的相关曲线，通过对比分析可得出以下结论：

（1）顶层位移标准差、各层位移方差最大值及层间位移方差最大值的对比都表现出PTRMD 受控结构远小于未受控结构，说明PTRMD装置对随机激励引起的结构振动具有良好的控制效果。

（2）多自由度结构1～3层的失效概率结果差异不大，从第4层开始PTRMD 受控结构的失效概率开始逐渐小于未受控结构，说明PTRMD 装置的应用不仅不会对结构可靠度产生负面影响，还会随着楼层的增加减小结构的失效概率。

（3）试验结果表明，一般情况下PTRMD 对受控结构位移幅值控制效果要优于PMD 装置，最优碰撞间距的设置也会受到激励特征的影响；质量比越大获得的最优减振率越高，质量比越小则装置对频率的敏感度越低，所以在具体的参数设计时要考虑减振率与鲁棒性之间的平衡协调。