弯曲元剪切波速试验中圆柱状试样的尺寸效应研究

高彦斌，郑晓军，王 浩，戴梓仪

（1.同济大学土木工程学院，上海 200092；2.同济大学物理科学与工程学院，上海 200092）

引言

土的剪切波速是很重要的土体参数，在岩土工程中具有广泛的应用，如计算土体的剪切模量，砂土场地的液化判别，划分建筑场地类别等［1-4］。弯曲元法是一种简单快速地确定土的剪切波速的室内试验方法，常被安装在固结仪、三轴仪、动三轴仪等土工仪器中测试标准尺寸试样（直径50 mm、长度100 mm 或直径40 mm、长度80 mm 的圆柱状试样）的波速［5-6］。由于弯曲元法原理简单，测试方便，近年来，其被越来越多地推广应用于测试无侧限条件下非标准尺寸试样的剪切波速［7-8］。然而利用弯曲元测试土的剪切波波速时，接收波波形会受到多种因素的影响，从而影响剪切波速的测算精度。国内外学者从消除激发波近场的角度进行了大量的研究工作，认为试样的尺寸、弯曲元的尺寸、测试系统与系统延时、激发信号的类型以及频率的选择等都是影响弯曲元准确测试剪切波速的因素［9-13］。但由于以往的研究集中在利用装有弯曲元的土工仪器测试标准尺寸试样的剪切波速，从而对试样尺寸影响波速测试的认识不够全面。文中着重研究在无侧限条件下，利用弯曲元测试非标准尺寸试样波速时，试样尺寸对测试结果的影响，并将与试样尺寸相关的近场效应与边界反射统称为试样的尺寸效应。

近场效应，即当传感器间距较近时，发射传感器近场产生的压缩波对接收传感器接收到的剪切波波形的影响。一些学者研究了利用试样的尺寸消除近场效应的方法，结果表明，近场效应与测试距离L与波长λ之比（即L/λ）有关，当L/λ大于2 时，近场影响就可以忽略［9］。Leong 等［14］则建议L/λ=3.33 测试结果最佳。这些研究结果表明，当发射波的波长一定时，试样尺寸越长越有利于提高测试精度。然而在以往的测试中，发现即使L/λ 足够大时，接收波形起跳点处仍然会出现反向提前到达的波形［7］。一些学者认为这种现象与试样尺寸有关，特别是圆柱状试样的长细比，Ingale 等［12］给出已有试验中采用的试样的长细比L/D，大都在0.4至2.28之间且大部分为2.0，但对长细比影响波速测试的机理认识还不充分。Arroyo等［15］利用内径为98.5 mm的固结仪测量了4 个不同长度圆柱状黏土试样的剪切波速，发现试样的长细比对波形以及测试结果有显著的影响。后来Arroyo 等［16］通过数值分析研究了试样长细比对接收波形的影响，认为试样侧向边界反射的P波影响了接收到的S波波形。Lee等［17］也得出相同的结论，并通过设计一组利用多次反射来计算试样波速的试验进一步验证了弯曲元波速测试中边界反射的存在。

利用弯曲元测试剪切波速VS的原理为：

式中：L'为直达剪切波的传播距离，即弯曲元传感器尖端之间的距离；Δt为直达剪切波在试样中的传播时间。由于上述各种影响因素的干扰，剪切波的传播时间Δt的正确判断成为一个难题。时域法是根据发射波形和接收波形的一些特征点位置来判断剪切波传播时间Δt的一种非常常用的方法，如图1 所示，图中S0、P0分别代表发射波的起跳点与峰值点，P1、S1、S2、S3分别代表接收波的峰值点、接收波的起跳点、反相峰值点、反相峰值点后回复到原点的点。这样，判断剪切波传播时间的方法就有以下4 种：（1）S0-S1（起跳点法，start-start method）；（2）S0-S2；（3）S0-S3；（4）P0-P1（峰峰法，peak-peak method）。这些方法中，早期的研究中大多采用的是S0-S1（起跳点法）和P0-P1（峰峰法）法。后来经过系列比较实验，部分学者认为S0-S3法较为合适、接近共振柱法所得波速［18-22］，部分学者［23］认为采用S0-S2是可靠的。Arroyo 等［15］在对不同长度的土样测试结果分析中则发现无论哪种方法都不可靠，较为复杂的频域法和互相关法也并不能给出比时域法更准确的结果。目前对时域法中特征点的选用仍存在较大的争议，采用哪个特征点确定剪切波传播时间得到的波速更为准确仍是一个值得研究的问题。

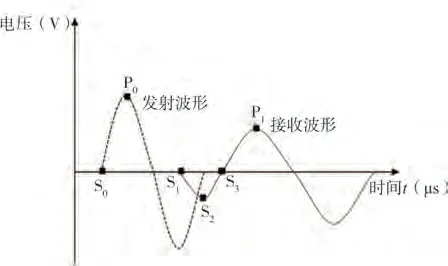
图1 特征点法示意图Fig.1 Schematic diagram of characteristic point methods

综上，由于目前利用弯曲元测试不同长度试样剪切波速的试验成果仍然较少，试样尺寸对测试结果的影响规律及其机理仍然不太明确。文中通过研究圆柱状试样的尺寸效应对测试结果的影响，并与已有的结果进行对比分析，探讨尺寸效应产生的机理以及简化分析模型。在此基础上，讨论了不同数据处理方法对该效应的影响。

1 测试系统与方案

1.1 测试系统

弯曲元（Bender element）是一种由压电陶瓷片制成的传感器，本文中采用的压电陶瓷片长×宽×厚为15 mm×15 mm×0.5 mm，将其插入一个金属外壳内，突出的悬臂端长为2.5 mm，压电陶瓷片与金属外壳间填充环氧树脂防水层与电磁屏蔽材料，厚度为2 mm，如图2 所示。弯曲元波速测试系统布置如图3 所示，由信号发生器产生的单周期正弦信号用作发射信号，发射信号的电压幅值为5 V。发射弯曲元将电信号转换为剪切波信号，通过试样传播到接收弯曲元后，剪切波信号被转换成电信号，由电压放大器放大后被数据采集卡采集，最终得到接收波形。试验时将弯曲元固定于可移动支架上，将弯曲元悬臂突出部分插入试样两端，保证传感器与试样耦合良好后，进行无侧限波速测试。弯曲元波速测试系统的系统延时为20 μs，在波速计算时自动扣除了这部分系统延时。

图2 试验采用弯曲元Fig.2 Bender elements used in test

图3 弯曲元波速测试系统布置图Fig.3 Bender element wave velocity test system

1.2 试样与测试方案

本次试验采用的是直径D=6 cm 的圆柱状试样，其材料为一种泡沫塑料，采用这种材料是因为一方面其与土样类似，是一种均质材料；另一方面可以尽量保证试验中采用试样的物理性质基本相同，避免因试样性质差异过大带来的试验误差。本次试验共使用了6 个不同长度的试样，长度分别为L=2 cm，3 cm，5 cm，6 cm，9 cm，12 cm，其长细比L/D相应地为0.33～2（见表1）。试样的实物图见图4。

图4 试样实物图Fig.4 Samples used in test

发射信号由一个单周期的正弦波激发，这是因为根据之前的学者研究，采用不同的激发波类型（正弦波、方波）测试同一试样会得到相似的接收波形，且正弦波适用于不同种类、软硬的土样，而方波由不同频谱组成，较正弦波而言会更影响接收波形态，因此文中采用了正弦波作为激发波。［11］同时为研究激发信号频率f对接收信号的影响，文中采用了典型的5 kHz和10 kHz作为激发频率，由于信号衰减的影响，仅在L=2 cm的试样中进行了更高频率（20 kHz）的测试。根据测试频率f可以计算得到每个测试工况下对应的波长λ与波数L/λ，

式中：VS为试样波速；T为发射波周期；f为发射波频率，具体数值见表1。已有研究结果表明，为了保证接收波的强度，波数L/λ尽量控制在4以内。假定该材料的波速为150 m/s（与下文的测试结果相近），计算得到的波数L/λ见表1。由表可知，本次测试中的波数L/λ=0.67～8，大部分在4以内。

表1 试验方案及测试参数Table 1 Test scheme and parameter values of measurement

2 长细比L/D对波形的影响

图5展示了测得的6个试样在不同频率下的接收波波形。下面从接收波形的起跳点S1出现的时间以及接收波的形态2方面来分析长细比对测试结果的影响。

由图5（a）、（b）可以看出，对于L=2 cm 和3 cm 的2个试样（长细比L/D=0.33和0.5），试验测得的接收波中起跳点S1（即图中标出的黑色圆圈）清晰可辨，未出现图1中的异常现象。对于测试频率的影响，可以看出尽管不同测试频率下的接收波形有所差别，即频率越高，信号衰减程度越大，幅值越小，但是起跳点的位置却几乎一致，并不受测试频率的影响。因此，这些波形可以看作是不受近场效应影响的波形，采用S0-S1法（起跳点法）得到2个试样的剪切波波速VS分别为154 m/s和150 m/s。因此，取平均值152 m/s作为该试验材料的剪切波速标准值。以此为标准，给出试样长度L=5 cm、6 cm、9 cm、12 cm 下的直达剪切波理论传播时间Δt，这个理论时间用黑实线标注在各图中。

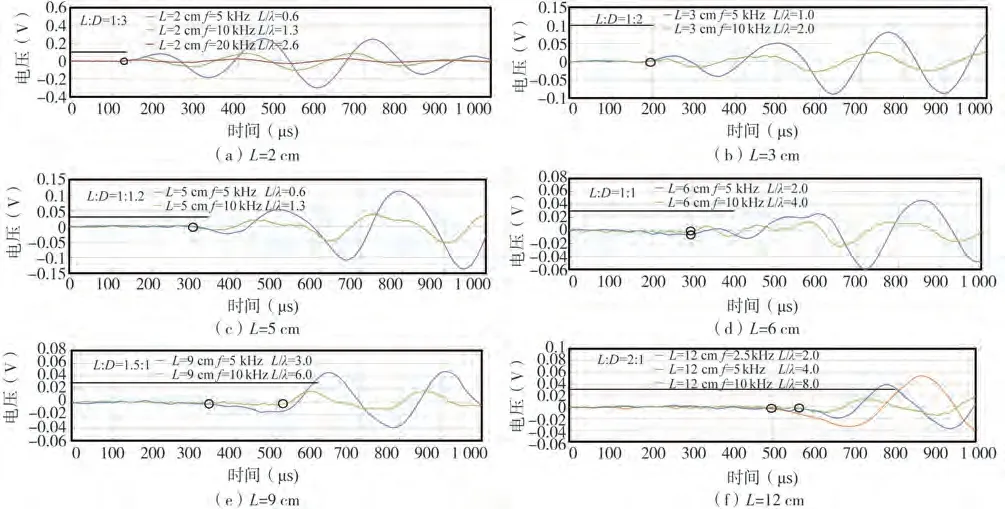
图5 不同长度试样的接收波波形图Fig.5 Received signals of samples with different lengths

从图5（c）～（f）给出的试样长度L=5 cm、6 cm、9 cm、12 cm（长细比L/D=0.83，1，1.5，2）的接收波形可以看出，随着试样长细比的增大，接收波起跳点附近的波形变得复杂多样，起跳点的位置也变得不容易判断。图中的黑色圆圈标出了起跳点的位置，带有一定的主观性。在L=5 cm（L/D=0.83）情况下，波形出现了反相情况，也就是文献中所讲的近场效应所表现出来的主要特征。另外，起跳点出现的时间也要比理论时间稍早一些，不过差别并不大。在L=6 cm（L/D=1）情况下，起跳点出现的时间明显早于理论时间，而波形仍然表现为同相。当L=9 cm、12 cm（长细比L/D=1.5，2）时，起跳点出现的时间进一步提前，且波形基本表现为反相。总体上看，存在测试频率越大、起跳点出现时间越晚的规律，得到的结果也就越准确。但是，增大频率和波数会造成信号的显著衰减，同时通过比较利用不同频率测试各长度试样得到的接收波形，可以发现改变测试频率只会改变接收波的幅值，而不会改变接受波的形状，因此对于长细比较大的试样，在实际测试中增大频率并不能提高测试质量。

图6给出了以往常用的2种方法，即S0-S1法（起跳点法）和P0-P1法（峰峰法）得到的剪切波的传播时间Δt。其中S0-S1法的Δt由图5 中的黑色圆点对应的时间确定，P0-P1由发射波和接收波的第一个峰值点的时间差来确定。可以看出，当试样长细比较小时（L/D＜0.83），这2 种方法在不同测试频率下的结果均一致；而随着试样长细比的增大（L/D＞0.83），2种方法给出的传播时间均小于理论传播时间，而采用S0-S1法时传播时间会被严重低估，尤其是在频率较低的情况下。

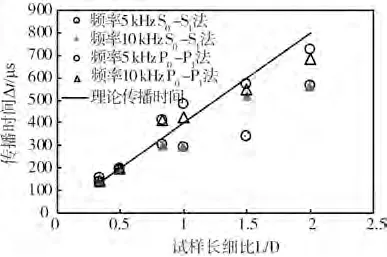
图6 S0-S1法和P0-P1法确定的剪切波传播时间ΔtFig.6 Shear wave propagation time Δt determined by S0-S1 method and P0-P1 method

3 波速计算结果分析

3.1 文中测试结果

根据图5 给出的波形，采用前面给出的4 种特征点方法S0-S1、S0-S2、S0-S3、P0-P1来确定剪切波波速VS，其结果如图7 所示，据此进一步计算了其与实际波速的比值（即波速比VS/150），如图8 所示。由图7 可以看出，当长细比小于0.83时，不同数据处理方法得到的波速差别不大，均接近实际波速。当长细比大于等于0.83 时，采用S0-S1法得到的波速远大于实际波速，采用其他方法在L/D为0.83 和1.0 情况下会低估试样波速，而在L/D 增大到1.5和2.0情况下则会高估试样波速。由图8可得，从数据处理的角度看，S0-S3法和P0-P1法较其他方法测得的结果整体误差较小（即（VS/150-1）×100%），在20%之内。而从5 kHz 和10 kHz 这2种频率的测试结果来看，以上规律似乎不随测试频率的改变而发生显著改变。也就是说，在长细比较大的情况下，通常采用的提高测试频率的方法并不会改善测试结果的准确性。

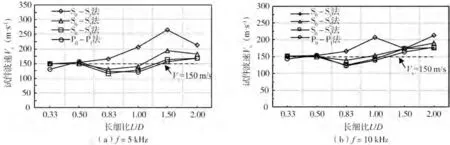
图7 不同特征点法得到的剪切波波速Fig.7 VS determined by different characteristic point methods

图8 不同特征点法得到的波速比Fig.8 Velocity ratio for different characteristic point methods

3.2 与其他测试结果的对比

Arroyo等［15］采用直径为90 mm的Gault黏土样进行了侧向无约束状态下的弯曲元波速试验。根据经验，这种黏土的实际波速约为98 m/s。采用土样的长度在70 mm 至150 mm 之间，长细比L/D在0.7 至1.5 之间。作者采用了5 种数据处理方法来计算波速，得到的结果见图9 所示，其中V0对应文中特征点法中的S0-S1所测试样波速，作者认为P 波先于S 波到达，先到达的P 波使得S 波的到达点难以识别，假定了2 个其他特征点作为S 波的到达时间，V1、V2为作者根据自己确定的S 波到达点计算所得的波速，VCC和VCS分别为互相关法与频域法所测波速。可以看出，由3 种特征点法计算得到的波速显著高于实际波速，其中起跳点法（V0）得到的波速最大，这与文中的结果是一致的。而2 种较为复杂的方法互相关法与频域法得到的波速要小于实际波速，可见采用这些方法并不能提高测试的精度。另外，波速测试结果与试样的长度之间并不存在一个单调的关系，呈现出忽大忽小的规律，这与文中得到的结果也是一致的。

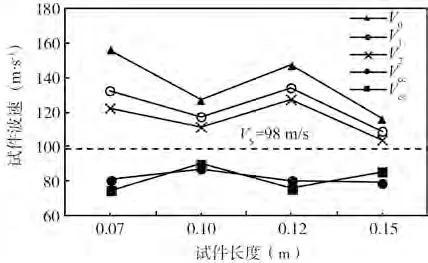
图9 Arroyo等测得的Gault黏土波速Fig.9 Vs of Gault clay samples measured by Arroyo

4 基于P波反射的尺寸效应分析

文中试验中接收波的提前起跳现象很可能是由P 波经边界反射后先到达接收传感器造成的。2种波形的相互干扰使传感器接收到的波形呈现出复杂的形态。下面尝试用这个机理来具体解释上述试验结果。

如图10 所示，圆柱状试样长为L、直径为D。发射传感器产生一个波场，包括向正前方传播的S 波以及侧向传播的P波。直达S波在试样中的传播时间为tS可表示为：

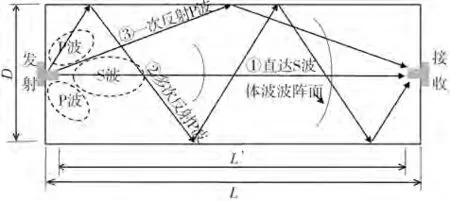
图10 基于P波反射的分析Fig.10 Analysis based on P-wave reflection

在所有的P 波中，传播距离最短的最先到达接收端的为图中给出的反射一次的P 波，其传播时间为tP可表示为：

根据弹性力学，各向同性弹性杆件中S波波速VS和P波波速VP与弹性模量E、泊松比μ、密度ρ的关系为：

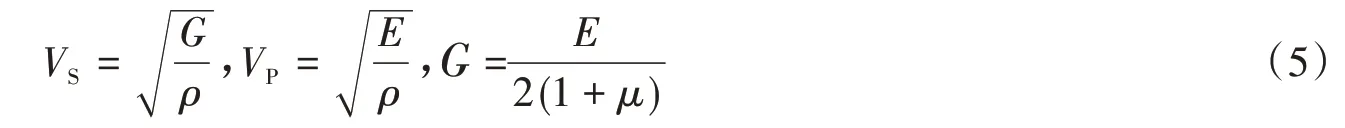
这样得到2种波速之间的关系为：

这样，2种波的传播时间之比可以表示为：

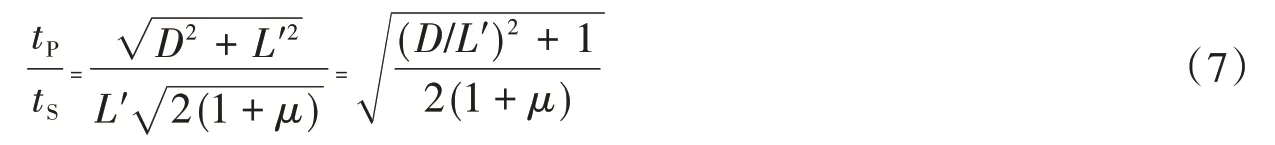
显然，当tP=tS时，直达S波与一次反射P波同时到达；而当tP＜tS时，P波将先到达。因此可以得到P波先于S波到达的条件是：

定义一个临界长细比，当试样长细比大于该参数时，就会产生P波反射的干扰。根据式（8），临界长细比可表示为：

可以看出，临界长细比只与泊松比μ有关。假设μ=0.3，代入公式得到临界长细比的典型数值为0.794。这与实验中发现的当L/D达到0.83（L=5 cm）时波形出现明显变化的结果相吻合。

根据式（7）可以进一步得到采用起跳点法得到的波速V*与试样的真实剪切波速Vs真实之间比值为：

将典型值μ=0.3代入式（8），给出的V*/Vs真实随L'/D的关系曲线如图11所示。当L'/D大于0.83后，测试误差随L'/D的增大而单调增大，V*/Vs真实的最大值约在1.5左右。

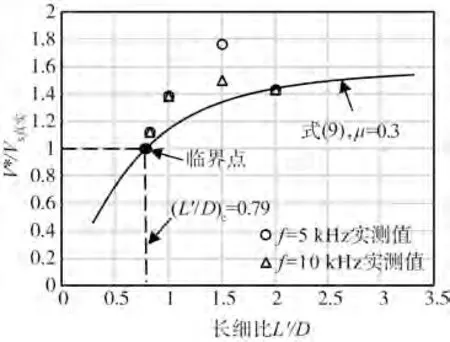
图11 理论分析与实测结果的对比Fig.11 Comparison between theoretical analysis and experimental results

图11 中也给出了与文中实测结果的对比。可以看出，理论分析与实测结果的规律总体上是一致的，式（10）总体上可以反映尺寸效应对波速测试的影响。但实测结果比理论预测要复杂一些，这一方面是由于试验材料的泊松比μ不会精确是0.3，另一方面是实际测试时接收波形除了受经边界侧向反射后到达的P波影响以外，还可能受经试样端面反射及沿侧壁传播到达的P波的影响，这有待进一步研究。

5 结论

（1）在弯曲元剪切波速测试中，随着试样长细比的增大，接收波形出现复杂的形态，接收波起跳点提前出现导致测试波速较实际值偏大，起跳点法给出的剪切波波速受试件尺寸影响最大，且受测试频率的影响不明显。一些复杂的数据处理方法并不能改善测试结果的准确性。

（2）采用不同长细比试样得到的结果不能用近场效应来解释。P 波反射理论总体上可以反映实测结果中存在的尺寸效应。分析得到试样的临界长细比约为0.79，当试样的长细比大于该值时，P波侧向反射成为影响测试结果的一个因素。