砂土液化剪切波速判别方法的对比分析

刘红帅，宋东松，冯 震

（1.河北大学岩土工程研究所，河北保定 071002；2.河北极致地震预防服务有限公司，河北保定 071002）

引言

土壤液化是砂土或粉土分布地区导致地基失效和结构受损的直接原因。自唐山地震以来，我国先后颁布实施的抗震设计规范均提出了土壤液化判别要求，经过若干次破坏性地震的实际检验，规范的实施证明其减轻液化灾害的效果显著。目前，我国建筑抗震设计规范指定采用标贯法，岩土勘察规范条文说明推荐剪切波速液化判别法。实践表明，标准贯入试验锤击数是不连续的，而且重复性差；剪切波速值则是连续的、测试方便，现剪切波速液化判别已逐步成为研究热点［1-4］。因此，开展剪切波速液化判别的研究具有重要的工程应用价值。

液化判别方法大致可分为3类：经验方法、试验-理论分析方法和综合方法［5］。对比中外抗震规范不难看出，中国规范以标贯法为主［6］，是最具代表性的经验方法；美国规范以Seed简化法为主［7］，是试验-理论分析方法的典型代表。从理论上讲，后者的判别精度要比前者高，但原状砂土的取样成本和技术要求非常高，通常以扰动砂土样作为试验样本，导致其试验精度与实际差别显著，而且时间和经济成本偏高；前者属于工程类比法，但只要具备相当数量的统计样本并选取恰当评价指标，其判别可靠度亦有保证。

陈国兴等［8］最近对液化判别方法作了全面系统的回顾与评述，在此就不再对此方面进行赘述。目前各种剪切波速液化判别公式所使用的数据集不完全相同，且相互间缺乏较为客观的对比评价，可信度较低。为此，基于国内外公开发表的数据，建立液化判别法检验的剪切波速数据库，选取现行《建筑抗震设计规范》标贯法［6］的转换公式和《岩土工程勘察规范》推荐法［9］、陈国兴等公式［10］、孙-袁公式［3］、Andrus-Stokoe 公式［11］作为典型代表，对比其自身表现和判别结果的差异，给出使用建议，为合理选用液化判别法提供重要参考。

1 剪切波速判别方法

目前，国内外大多数学者基于多个震例的调查数据建立了剪切波速液化判别式，具有代表性的成果有：Andrus 等［11］根据世界各地26 次地震70 余个典型地震液化场地的剪切波速资料，给出了砂土液化临界关系曲线；陈国兴等［10］根据Kayen、Andrus、Saygili 和Chu 等整理的现场液化资料数据库，给出了适用于核电等重大工程场地的土壤液化临界关系曲线；孙锐等［3］利用Andrus 数据库，提出了适用于砂土和粉土的双曲线形式液化判别公式；胡庆等［12］利用Kayen 等提供的数据库，建立了饱和砂土的双曲线液化判别公式；周燕国等［13］结合弯曲元和动三轴试验结果，改进以往的砂土剪切波速判别公式；Ahmadi等［14］基于室内动三轴试验以及弯曲元试验，提出了一种分别适用于Babolsar砂土和Firoozkooh砂土的液化判别方法。

同时，也有少数学者基于单一震例的调查结果给出了特定地区的判别公式。例如，Kayen等［15］利用1989年Loma Prieta 地震液化场地的剪切波速资料，给出了砂土液化临界关系曲线；丁伯阳等［16］根据1988 年宁夏灵武地震砂土液化资料，提出了适用于西北地区砂土的液化临界关系曲线；赵玉倩等［17］依据新疆场地实测数据提出了适用于新疆地区的剪切波速液化判别公式。

值得指出的是，上述成果均未考虑砂土和粉土液化特性的差异。石兆吉等［18］根据海城地震、唐山地震中砂土、粉土液化与剪切波速等相关资料，提出了2类土的液化判别公式；谢生荪等［19］以Seed简化方法为基础，结合山西某电厂现场和室内相关资料，提出了分别适用于该区域场地砂土和粉土的液化判别公式。

考虑到多个震例的综合结果更能反映地震动的平均效应，具有更广泛的代表性，因此，选取多个震例的土壤液化剪切波速判别式作为研究对象。结合我国工程实际和当前液化剪切波速判别法的最新成果，选取了5种代表性方法，具体如下：

1.1 建规转换法

《建筑抗震设计规范》（GB50011-2010）（2016 年版）［6］中的标贯法是我国应用最广泛的液化判别法，其原理是比较土层标准贯入试验值N和临界值Ncr的大小，当Ncr≥N时，应判别为液化，否则为不液化，其最大判别深度为20 m，液化判别计算公式如下：

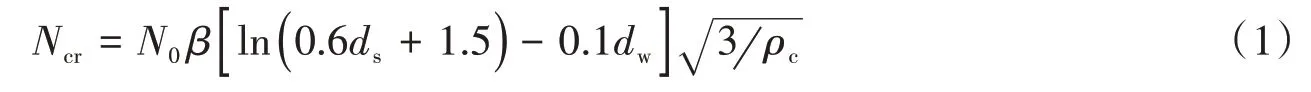
式中：Ncr为液化判别标准贯入锤击数临界值；N0为液化判别标准贯人锤击数基准值，按表1 取值；ds为饱和土标准贯人点深度（m）；dw为地下水位（m）；ρc为黏粒含量百分率，当小于3 或为砂土时，应采用3；β为调整系数，设计地震第1组取0.80，第2组取0.95，第3组取1.05。该公式适用范围为20 m以内的饱和砂土、粉土。

表1 液化判别标准贯入锤击数基准值N0Table 1 Liquefaction discrimination standard penetration hammer number reference value N0

为便于与剪切波速液化判别方法对比，计算给出标贯值液化临界线，并采用剪切波速与标贯值和埋深的经验公式，转换给出了与标贯法相对应的临界剪切波速曲线（以下简称建规转换法）。具体做法如下：采用GB50011-2010 规范法中峰值加速度0.1 g、0.2 g 和0.4 g 作用下的临界标贯值曲线，作为地震烈度Ⅶ、Ⅷ和Ⅸ度的临界标贯值曲线，其中设计地震取第一组β=0.80。利用张忠利［20］提出的适用于细砂的剪切波速与标准贯入锤击数和埋深的关系Vs=85.0111ds0.002N0.363（N为标准贯入锤击数；ds为土层埋深（m）），将标准贯入锤击数临界值转换为剪切波速临界值，公式如下：

1.2 岩规法

《岩土工程勘察规范》［9］（GB50021-2001）（2009 年版）是我国应用最广泛的规范之一，其条文说明推荐给出的剪切波速液化判别方法（岩规法）也对工程界有重要的影响，该方法是石兆吉等［18］根据海城地震、唐山地震中砂土、粉土液化与剪切波速等相关资料提出的，其液化临界剪切波速公式表达为：

式中：ds为土层埋深（m）；dw为地下水位（m）；ρc为黏粒含量；Vs0为与烈度、土类有关的经验系数（m·s-1），按表2 取值。该公式适用范围为15 m 以内的饱和砂土、粉土。

表2 不同烈度下Vs0 值Table 2 Vs0 value under different intensity m·s-1

1.3 陈国兴等公式

陈国兴等［10］利用Kayen、Andrus、Saygili 和Chu 等给出的资料，建立了最全面的剪切波速液化数据库，提出适用于核电等重大工程场地砂土和粉土液化临界曲线：

式中：Vs1为修正剪切波速（m·s-1），Vs1=。

1.4 孙-袁公式

孙锐等［3］利用早期的Andrus 数据库对岩规法和Andrus 方法进行检验，发现了二者存在的问题，采用Kayen数据库，提出了双曲线形式的剪切波速液化判别公式：

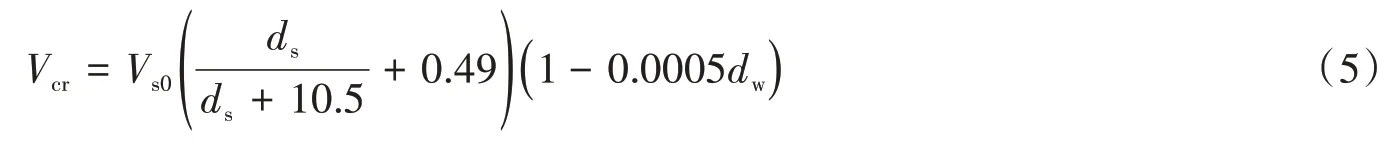
式中：Vs0按表3 取值。该公式适用范围为25 m 以内的饱和砂土和粉土。

表3 不同加速度下Vs0 值Table 3 Vs0 value under different intensity m·s-1

1.5 Andrus-Stokoe公式

目前国外应用广泛的基于剪切波速的土壤液化判别式是Andrus 等［11］提出的计算方法，其要点为计算砂层受到的地震剪应力比CSR和抗液化应力比CRR。其中CSR的表达式为：

式中：amax为地表峰值加速度（g）；g为重力加速度（m·s-2）；σv为上覆土压力（kPa）；为有效上覆土压力（kPa）；rd为应力折减系数，具体取值参考原文。CRR的表达式为：

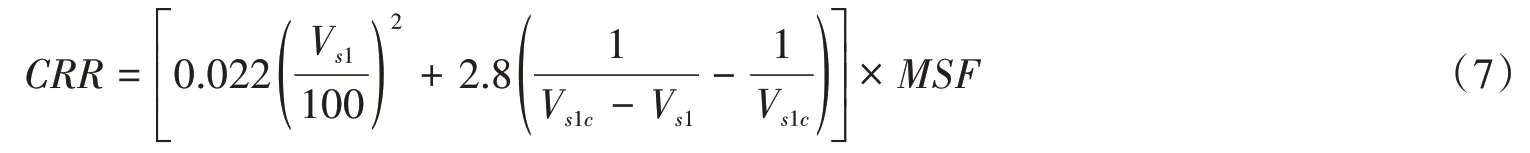
式中：Vs1为修正剪切波速（m/s），Vs1=；Vs为实测剪切波速（m·s-1）；Vs1c为液化剪切波速上限（m·s-1），当细粒含量FC≤5%时，Vs1c＝215 m·s-1；5%＜FC≤35%时，Vs1c＝215-0.5（FC-5）m/s；FC＞35%时，Vs1c＝200 m·s-1。MSF为震级修正系数，当震级Mw≤5.2时，MSF=1.82，当Mw＞5.2时，MSF=6.9exp（-Mw/4）-0.06。

2 数据库及主要特征

2.1 数据来源

Andrus等［21］给出了液化场地剪切波速数据，包括26次地震中70个场地的数据，总计226组；Kayen 等［22］液化数据库包含了35次地震中的415例场地液化资料；由于中国规范仅对设防烈度在Ⅶ度-Ⅸ度（0.09 g～0.75 g）［23］范围的可液化土进行液化判别，因此，文中取此范围的数据为有效数据，以及剔除Andrus等和Kayen等数据库中重复的数据和个别异常点后，总计得到525组样本，建立了文中的数据库，如表4所示。

表4 数据样本Table 4 Data sample

由于岩规法只给出了地震烈度为Ⅶ度、Ⅷ度、Ⅸ度时的判别式，为便于比对，故按照《中国地震动参数区划图》［23］（GB18306-2015）规定的场地地震动峰值加速度与地震烈度对照表，对上述数据库地震加速度进行地震烈度归档，并以地震烈度分组给出了统计结果，如表5所示。

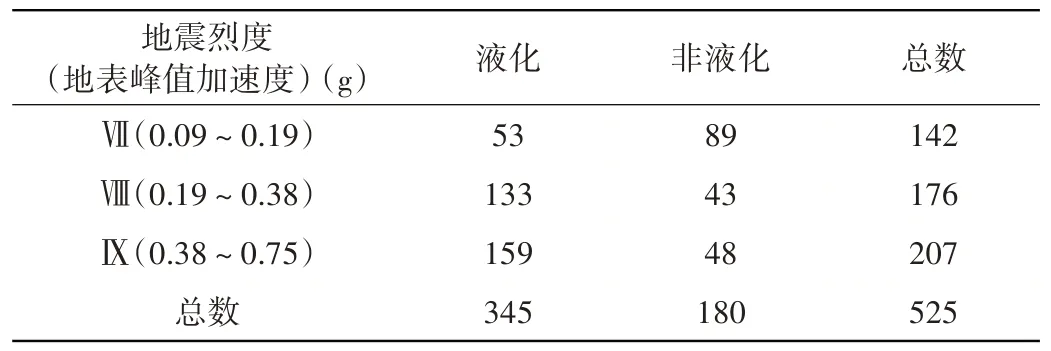
表5 以地震烈度为基础的统计分类Table 5 Statistical classification based on earthquake intensity

2.2 剪切波速分布特征

图1给出了剪切波速与埋深的散点分布图。已有记录液化点埋深基本分布在2～18 m间；在地震烈度Ⅶ、Ⅷ、Ⅸ度时，液化点最大剪切波速分别为170 m/s、185 m/s、220 m/s；非液化点埋深与液化点大体相同，在地震烈度Ⅶ、Ⅷ、Ⅸ度时，液化点与非液化点均有显著的混杂现象，Ⅶ、Ⅷ度有明显的液化与非液化分区现象。

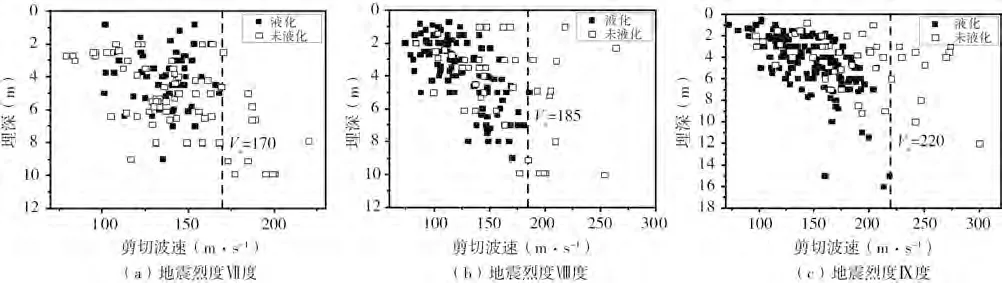
图1 剪切波速与埋深关系Fig.1 The relationship between shear wave velocity and depth

3 剪切波速判别方法对比

3.1 液化判别式对比

对比选择的5种判别式可以发现，液化判别式主要分为2类：一类是以地震烈度或地表峰值加速度作为剪切波速修正的基准值建立的Vcr-ds关系（建规转换法、岩规法、孙-袁公式）；另一类是根据土壤受到的地震剪应力比CSR及其抗液化应力比CRR建立的Vcr-CSR关系（陈国兴等公式、Andrus-Stokoe公式）。为方便对比2 种不同形式的判别方法，对第二类判别公式进行等价替换，取CSR=CRR，求得此时的临界剪切波速。当实测剪切波速位于临界线左侧其判别结果为液化，否则为不液化。假定地下水位为2 m，进一步求出临界实测剪切波速。

图2 给出了各判别式在不同地震烈度下的临界剪切波速曲线。与现场实际调查数据相比，建规转换法明显保守；岩规法当趋于地表时，液化土层埋深越浅判别结果越危险，当趋于20 m时，埋深越大越保守，当埋深为20 m时，在地震烈度为Ⅶ度、Ⅷ度和Ⅸ度时，其剪切波速临界值为244 m·s-1、357 m·s-1和488 m·s-1，已有研究表明，土体标贯击数大于30（通过式（2）按标贯数为30 计算得到的剪切波速约为294 m·s-1）时，认为土体不液化［24］，而Ⅷ度和Ⅸ度时对应的临界剪切波速值分别比建规转换法的大21%和66%，明显保守。综上所述，岩规法要么偏于危险，要么偏于保守，明显偏离实际后续不再研究。

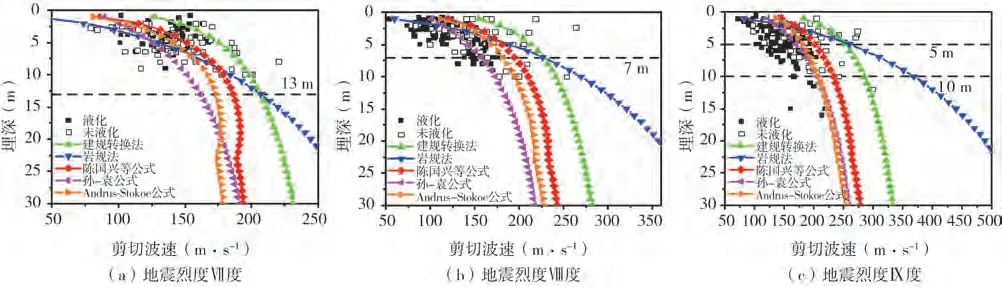
图2 砂土剪切波速液化临界曲线Fig.2 Critical curve of sand shear wave velocity liquefaction

陈国兴等公式和孙-袁公式的液化临界曲线大体分别为液化点的外包络线、液化点与非液化点的平均分界线。Andrus-Stokoe 公式临界曲线，Ⅶ度和Ⅷ度时，介于孙-袁公式和陈国兴等公式之间；Ⅶ度时浅表三者非常接近，向下接近陈国兴等公式，然后逐渐趋向孙-袁公式，最终小于孙-袁公式；Ⅷ度时，在埋深小于20 mn时更接近陈国兴等公式，但埋深大于20 m 时更接近孙-袁公式；Ⅸ度时，在埋深小于10 m 时比孙-袁公式略保守，但大于10 m 时，两者几乎重合。其中，Andrus-Stokoe 公式、陈国兴等公式的液化临界曲线出现回弯现象，尤其是在地震烈度为Ⅶ度时更为明显，造成这一现象的原因是这两个公式均采用的是CSR 理论中应力折减系数分段表达的缘故，目前超过10 m 后的应力折减系数求解问题并未很好解决，导致液化临界线不是统一的数学表达，而是沿深度分段表达拼凑而成，文献［25］对这一现象有详细解释。

为定量认识认识建规转换法、陈国兴等公式、孙-袁公式和Andrus-Stokoe公式之间的差异性，考虑到陈国兴等公式给出的液化外包络线，物理意义明确，因此选择陈国兴等公式作为评价基准，计算了建规转换法、孙-袁公式和Andrus-Stokoe 公式的相对误差，如图3所示。建规转换法的临界值明显大于陈国兴等公式的，埋深5 m时Ⅶ度、Ⅷ度和Ⅸ度下比陈国兴等公式分别大16%、18%、25%；岩规法的临界值明显基本都大于陈国兴等公式的，当埋深为5 m、地震烈度为Ⅶ度时比陈国兴等公式小14%，其他条件下均比陈国兴等公式大，埋深5 m 时Ⅷ度、Ⅸ度下比陈国兴等公式分别大5%、29%；Andrus-Stokoe 公式和孙-袁公式的临界值明显小于陈国兴等公式的，埋深5 m 时Ⅶ度、Ⅷ度和Ⅸ度下比陈国兴等公式分别小7%、7%、10%和17%、20%、16%。另外与陈国兴等公式相比，建规转换法、Andrus-Stokoe 公式和孙-袁公式这3 种方法随深度的增加相对误差有减小的趋势，但岩规法出现相反的现象。

图3 各方法差异性对比Fig.3 Comparison of differences between methods

3.2 基于地震实测数据的定量对比

本节依据表4的数据库，对比分析建规转换法、岩规法、陈国兴等公式、孙-袁公式和Andrus-Stokoe公式之间的差异。由于原始数据中部分砂土缺乏黏粒含量信息，采用建规转换法判别时，ρc统一取3；对于原始数据没有给出细粒含量FC的，使用Andrus-Stokoe公式判别时，统一按FC≤5%取值。

图4给出了地震烈度为Ⅶ、Ⅷ和Ⅸ度时各方法的液化判别成功率、非液化判别成功率、平均判别成功率和总体判别成功率。陈国兴等公式和建规转换法液化判别成功率均为100%，前者非液化判别成功率比后者略高，Ⅷ度时非液化判别成功率最高，不超过38%，总体平均判别成功率分别为58%和63%；文献［25］也对《建筑抗震设计规范》中标贯液化判别法（文中的建规转换法）的判别结果的可靠性进行了验证，其判别的结果为：总体平均液化判别成功率为99.3%，与文中的总体平均液化判别成功率100%基本一致，但其总体平均非液化判别成功率57.4%比文中的15%高，总体来说文中的判别结果具有一定的可靠性；岩规法液化判别成功率为85%～93%，非液化判别成功率为40%～43%，总体平均判别成功率分别为67%；孙-袁公式液化判别成功率为58%～2%，非液化判别成功率为69%～72%，总体平均判别成功率分别为67%；Andrus-Stokoe公式液化判别成功率不低于94%，但非液化判别成功率为37%～46%，总体平均判别成功率分别为68%。由此可见，液化判别成功率建规转换法和陈国兴等公式最高，其次为岩规法、Andrus-Stokoe 公式和孙-袁公式，而非液化判别成功率反之。平均判别成功率Andrus-Stokoe 公式最高，依次为孙-袁公式（岩规法等于孙-袁公式）、陈国兴等公式和建规转换法。

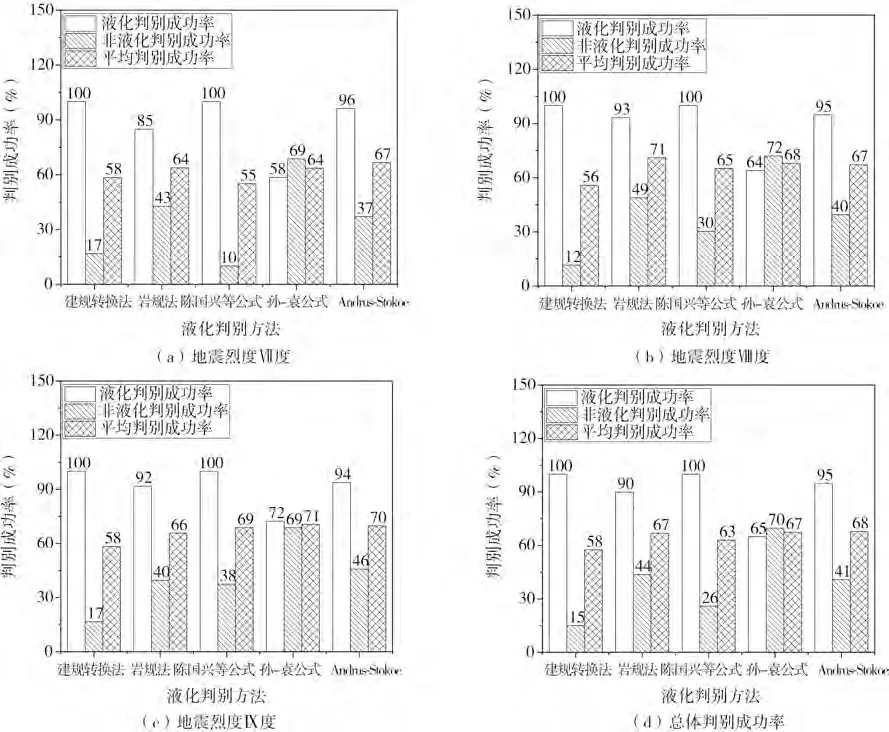
图4 现有方法对总体数据土壤液化的判别成功率Fig.4 The success rate of the existing methods in judging the overall data soil liquefaction

为了更直观地评价各种方法的优劣，采用相对误差作为评价指标，计算公式如下：

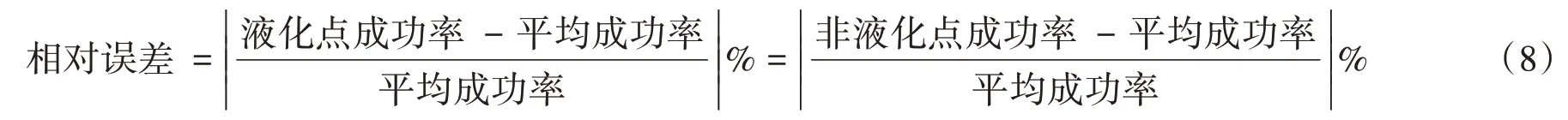
图5 给出了地震烈度Ⅶ、Ⅷ、Ⅸ度时各种方法判别成功率的相对误差。孙-袁公式的相对误差最小，依次为Andrus-Stokoe 公式、岩规法、陈国兴等公式和建规转换法。此外，孙-袁公式、岩规法、建规转换法和Andrus-Stokoe公式各地震烈度的相对误差变化不大，受地震烈度的影响最小。

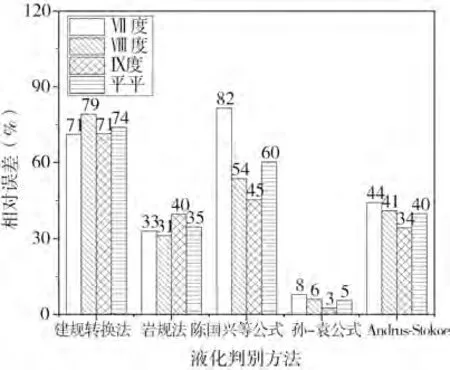
图5 总体数据判别成功率相对误差Fig.5 The relative error of the overall data discrimination success rate

4 讨论

砂土液化判别是减轻液化灾害的首道防线，历来受到学术界和工程界的高度重视。目前，我国应用最为广泛的是标贯法，剪切波速判别法也形成了重要的影响。美国已启动新一代液化判别方法的研究，建立了多源液化数据库（SPT，Vs和CPT），正在进行中，由此可见，液化判别方法仍尚未很好解决的问题，比如液化判别方法的检验。文中尝试使用剪切波速与标准贯入锤击数的经验公式将建筑抗震规范的标贯法转换为剪切波速形式，一并与国内最新发展的、国外最具影响的剪切波速判别法进行了对比检验，发现：陈国兴等公式为液化点的外包络线，而建筑抗震设计规范标贯法比陈国兴等公式在埋深5 m时Ⅶ度、Ⅷ度和Ⅸ度下分别大16%、18%、25%，尽管所使用的转换公式存在一定的不确定性，但明显保守，会造成工程上的浪费；孙-袁公式的液化临界曲线大体为液化点与非液化点的平均分界线，兼顾液化和非液化判别的均衡性；Andrus-Stokoe 公式存在不合理的回弯现象；岩规法埋深时偏于危险，埋深越大则越保守，明显偏离实际。

5 结论

（1）中国现行的《岩土工程勘察规范》中砂土液化剪切波速判别法明显偏离实际。

（2）中国现行的《建筑抗震设计规范》标贯法明显保守，造成工程上的浪费。

（3）陈国兴等公式给出的是外包络线；孙-袁公式给出的大体为液化点与非液化点的平均分界线，兼顾液化和非液化判别的均衡性；Andrus-Stokoe 公式介于陈国兴等公式和孙-袁公式的中间，但存在不合理的回弯现象。

值得指出的是，基于美国新一代液化数据库，进一步收集补充我国液化数据，发展多种（SPT，Vs和CPT）判别方法，利用经验公式进行转换，相互校核，更新建立更符合实际的我国新一代砂土液化判别公式。