采样序列长度及周波数对正弦参数拟合的影响
梁志国
(北京长城计量测试技术研究所 计量与校准技术重点实验室,北京 100095)
1 引 言
正弦波拟合测量方法有着广泛应用[1~13],有关其误差及不确定度评定也有众多研究[14~21]。
在正弦波形参数测量中,采样序列长度及序列所包含的周波数对测量及后续的曲线拟合有影响是有目共睹的,且已达成了一些共识。
通常,人们普遍认为采样序列长度越长,将可以获得更高的测量准确度以及更低的测量误差。在测量误差呈零均值随机分布的情况下,这无疑是正确的。Deyst等对正弦曲线拟合误差界的研究,依然延续了这一结论,并且给出了拟合误差界与序列长度成反比的确切结果[14]。然而,采样测量序列的误差分布规律很复杂,并不能简单认定为符合零均值随机分布;至少,它们均需要通过A/D转换环节,而A/D引入的量化误差并不完全呈现随机性,也很难属于零均值,因而,由正弦波采样序列拟合所获得的模型参数与采样序列长度之间的关系是否仍然符合上述共识,需要进一步研究予以确认。
关于采样序列所包含的周波数带来的影响,Deyst给出的结论依然是其拟合误差界随着周波数的增加呈震荡衰减趋势[14],并以仿真曲线方式给出了定量的结果。即随着周波数的增加,可以获得更高的拟合精度。实践证明,该结论是有条件的,并且对于正弦波的4个参数,其影响是有显著不同的。
本文后续内容,将针对采样序列长度和序列包含的信号周波数对正弦参数拟合误差界的影响展开仿真研究,同时,针对A/D位数的变化带来的影响也将进行仿真,其变化相当于序列信噪比发生了变化,也一定会给曲线拟合带来影响,希望通过研究获得具有一定规律性的结论。
2 基本思想及条件设定
2.1 基本思想
在波形数据采集中,测量条件通常涉及主观和客观两种条件。客观条件一般指被测量值的波形参量条件,包括幅度、频谱、噪声等信息。对于正弦信号,则指其幅度、频率、直流分量、失真等波形参量;它们不以人的意志为转移,很难被干预和变动。主观条件,则指可以通过自主选择而变化的测量条件,包括测量系统的量程、A/D位数、采样速率、存储深度、通频带、幅度测量误差、采样速率误差等。
正弦波形采样测量中,采样速率与信号频率是相关联量,两者之比是每个周波的采样点数,通过选择不同的采样速率可改变该比值;当采样速率固定后,采样序列的长短决定了其所包含周波数的多少。通过选取量程范围,改变被测信号幅度与量程的占比;通过选择不同A/D位数的测量仪器和系统,改变量化误差的大小。最终,改变正弦波拟合参数的误差界。
关于正弦曲线拟合,在大多数应用场合下,其采样序列长度在几十点到几千点之间,序列所含的信号周波数为几个至十几个周波。所用的采样系统A/D位数主要有8、12、16、24 bit几种。
其中,绝大多数数字示波器所用的A/D位数为8 bit,并且,在序列长度确定以及变化过程中,其它信号参数,例如幅度、直流分量、相位等,也将处于变化之中,它们共同作用的结果,将揭示拟合误差的实际变化情况。
2.2 仿真条件和指针设定
综合考虑各方面因素,选出具有相互独立性和系统完备性的左右量化误差影响的测量条件为:
1) A/D位数,用于确定量化水平及影响;
2) 采样序列包含周波数,确定周波数的影响;
3) 采样序列长度,即序列包含的样本点数,确定采样序列长度的影响;
4) 信号幅度,确定幅度变动的影响;
5) 初始相位,确定信号相位变化带来的影响;
6) 直流分量,确定直流分量变化带来的影响。
经过四参数正弦曲线拟合后,获得的指标特征参量为:
1) 有效位数误差界,以bit表述;
2) 拟合幅度误差界,以LSB表述;
3) 拟合频率误差界,以相对误差表述;
4) 拟合相位误差界,以度(°)表述;
5) 拟合直流分量误差界,以LSB表述;
6) 拟合残差有效值ρ,以LSB表述。
LSB(least bit)称为最小量化阶梯;当A/D位数为b、幅度量程为E时,有
(1)
理论上,
(2)
2.3 误差界搜索
正弦参数拟合的误差界,是在上述6项测量条件下,固定其中的5项,变化1项,搜索出该条件变化时,四参数正弦拟合所获得的有效位数、幅度、频率、相位、直流分量等5项指标的误差界。
在考察序列长度的影响时,则主要变化序列长度,辅助调整变化其它测量条件,着重分析出序列长度作为主导因素时,将给上述5项指标的拟合误差界带来的影响规律。
3 仿真实验及数据处理
使用电子计算机按照数学关系产生理想正弦数据,然后设定量程,按仿真的A/D位数进行量化,生成理想仿真序列。将该具有已知参量的仿真序列在选定的正弦波拟合软件中进行数据处理,获得拟合参数。
令仿真参数按照已知规律变化,获得变化条件下的拟合参数变化规律,并以此搜索各拟合参数的误差界。
3.1 仿真实验条件
为方便参数调控,不失一般性,设定包含6项测量条件的仿真实验条件如下:
1) A/D位数,基本参量为8 bit。
2) 序列样本点数,作为主变化因素时,变化范围为100~16 000点,1点步进,未特别说明时,序列样本点数为16 000点。
3) 采样序列包含周波数,作为辅助变化量时,变化范围为1~20个周波,1周波步进;未特别说明时,为20个周波。
由于正弦波采样测量序列拟合中,采样速率与信号频率两者是相关联的,构成每周波采样点数1个变量参数,故设定信号频率为1 Hz,称为归一化频率。采样速率因素作为变量。
实际仿真过程中,通过使用归一化频率1 Hz来调整采样速率,结合样本点数,最终构建周波数。
4) 信号幅度,使用归一化幅度1,作为辅助变化量时,在0.820 312 5×量程点处,其微观变化范围-0.5~0.5 LSB,0.05 LSB步进。
未特别说明时,幅度为0.820 312 5×量程;并以此设定量程范围。
5) 初始相位,作为辅助变化量时,变化范围为-180°~180°,10°步进,未特别说明时,初始相位为0°。
6) 直流分量,作为辅助变化量时,变化范围为-0.5~0.5 LSB,0.05 LSB步进,未特别说明时,直流分量为0。
3.2 仿真实验结果及分析
按照上述仿真实验条件,用数据点数参量为主变化因素,分别以幅度、周波数、初始相位、直流分量等参量为辅助变化因素生成实际的仿真条件,考察各指标要素的误差随着序列长度和其它因素而变化的情况。其中:
1) 幅度作为辅助变化量,获得如图1所述的误差界变化曲线波形;

图1 数据点数与幅度变化时的参数拟合误差界Fig.1 Error bound of sinusoidal curve-fit via both data numbers and amplitudes
2) 周波数作为辅助变化量,获得如图2所述的误差界变化曲线波形;
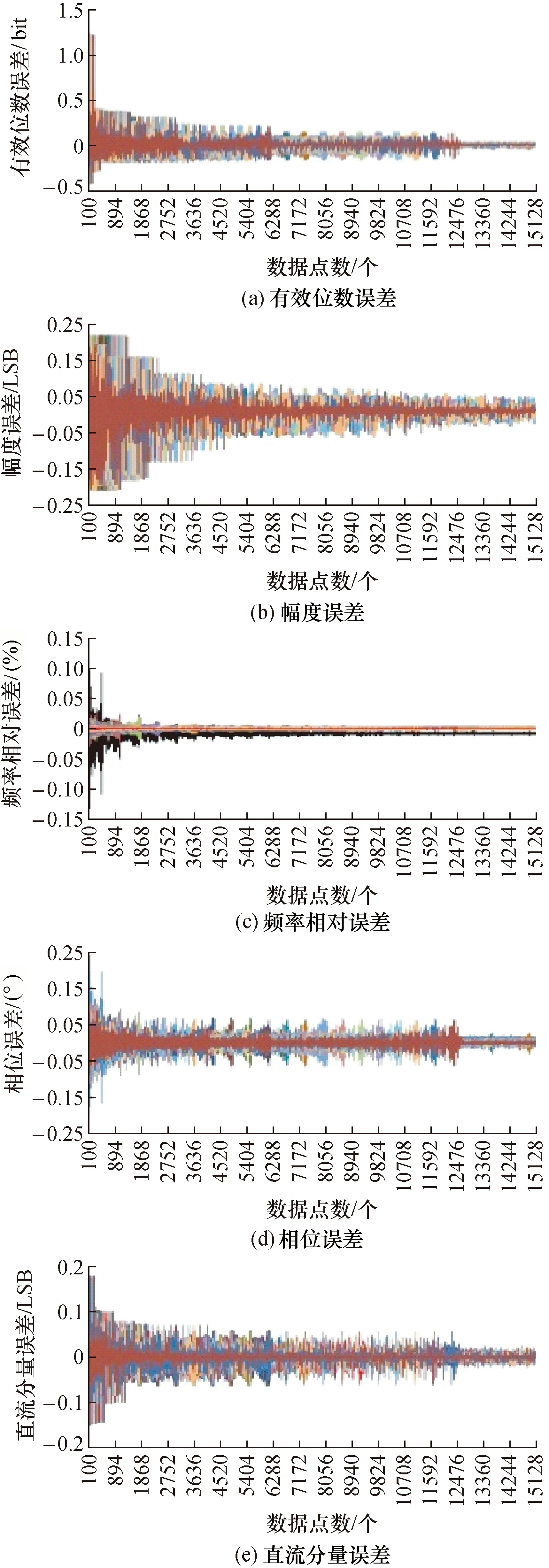
图2 数据点数与周波变化时的参数拟合误差界Fig.2 Error bound of sinusoidal curve-fit via both data numbers and periods
3) 初始相位作为辅助变化量,获得如图3所述的误差界变化曲线波形;
4) 直流分量作为辅助变化量,获得如图4所述的误差界变化曲线波形。
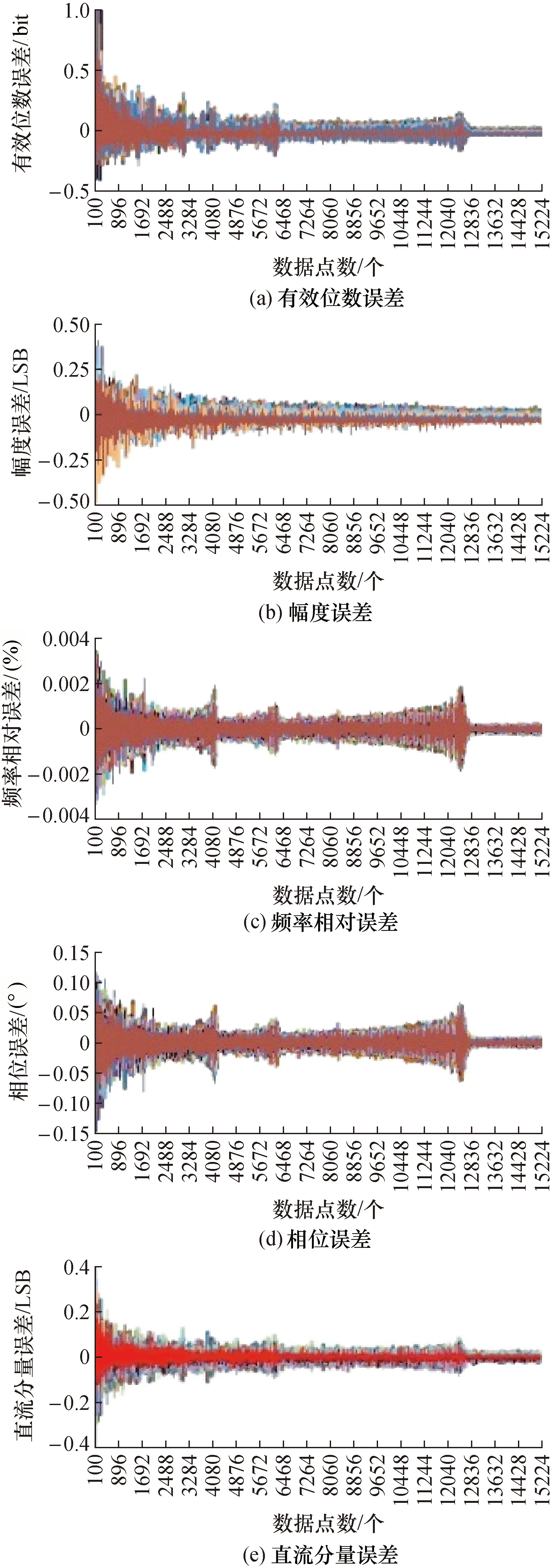
图4 数据点数与直流分量变化时参数拟合误差界Fig.4 Error bound of sinusoidal curve-fit via both data numbers and DC bias
从图1~图4可见,当其它辅助条件完全相同时,随着序列长度由小到大,各个指针参数的误差界指标总体上呈下降趋势。但并非单调下降,而是呈现出某种具有量化台阶式的量化特征。
经过对上述图1、图3、图4曲线波形的全面关联性规律分析发现,当信号周波数不变时,各个参数的误差界随序列长度和其它因素而变化的特征近似一致。即信号幅度和直流分量在量化码范畴微观变化时,以及信号初始相位变化时,对各个参数的误差界影响较小,可以近似认为其变化不显著。
图2中各个参数的误差界变化趋势与其它图中的差异较大。由图2可见,信号序列内包含的周波数与序列长度组合变化时,其误差量化台阶规律特征明显;并且,有效位数误差、频率拟合误差、相位拟合误差、直流分量拟合误差量化台阶的规律基本一致,而幅度拟合误差则规律特征不显著,其中,拟合幅度误差仍然可以认定为近似呈单调下降趋势。
而其它几项指标参量的误差,如频率误差、相位误差、直流分量误差、有效位数误差等,由于受到序列长度和序列内所含信号周波数的双重影响,均呈现有不同规则的量化台阶式降低规律。其中:
1) 图2(a)为动态有效位数误差随序列长度及周波数而变化的曲线波形;
2) 图2(b)为幅度误差随序列长度及周波数而变化曲线波形;
3) 图2(c)为频率误差随序列长度及周波数而变化曲线波形;
4) 图2(d)为相位误差随序列长度及周波数而变化曲线波形;
5) 图2(e)为直流分量误差随序列长度及周波数而变化曲线波形。
不失一般性,以图2(d)的相位误差曲线为例,当周波数固定时,序列长度从小到大变化时,相位误差曲线呈等间隔量子化阶梯式减小;如图5所示。其中,图5(a)为单周波序列,图5(b)为双周波序列,图5(c)为4周波序列,图5(d)为8周波序列。
称每一个误差阶梯宽度为台阶宽度。
在周波数相同时,量子化误差阶梯的每1个台阶宽度近似为等长度。
不同台阶的量值阶跃特征明显,其中,第1个误差台阶误差界高度最高,且属于台阶中间部分误差幅度较小,头尾部分误差幅度较大的马鞍形状。
从第2个台阶开始的后续台阶规律趋于一致。基本上是同一台阶内,误差有随着序列长度增加而缓慢增加或近似保持平稳趋势。
误差阶梯的台阶宽度与序列中含有的周波数呈线性比例关系,序列所含的信号周波越多,则拟合误差台阶宽度越宽。并且,仿真计算结果及变化规律表明,宽台阶近似于窄台阶的线性拉伸。在拉伸延展过程中,同一台阶误差带基本保持稳定,可以近似看作仅仅是长度展宽。观察分析周波数相邻的几条误差曲线,很容易发现该规律。
另外,特别需要说明的是,周波数为1时,幅度、频率、相位和直流分量的拟合误差界明显要比周波数为2及以上时大很多,其原因主要是周波数为1或更小时,所获得的采样序列波形很难出现幅度对称分布,因而在拟合时,能产生更大的回归误差。当周波数为2及以上时,情况趋于稳定和一致。
以相位误差曲线台阶末端跳变峰值来寻找各级量子化误差台阶末端点,结果如表1所示。

图5 相位误差随序列长度及周波变化情况Fig.5 Error of phase via data number and periods
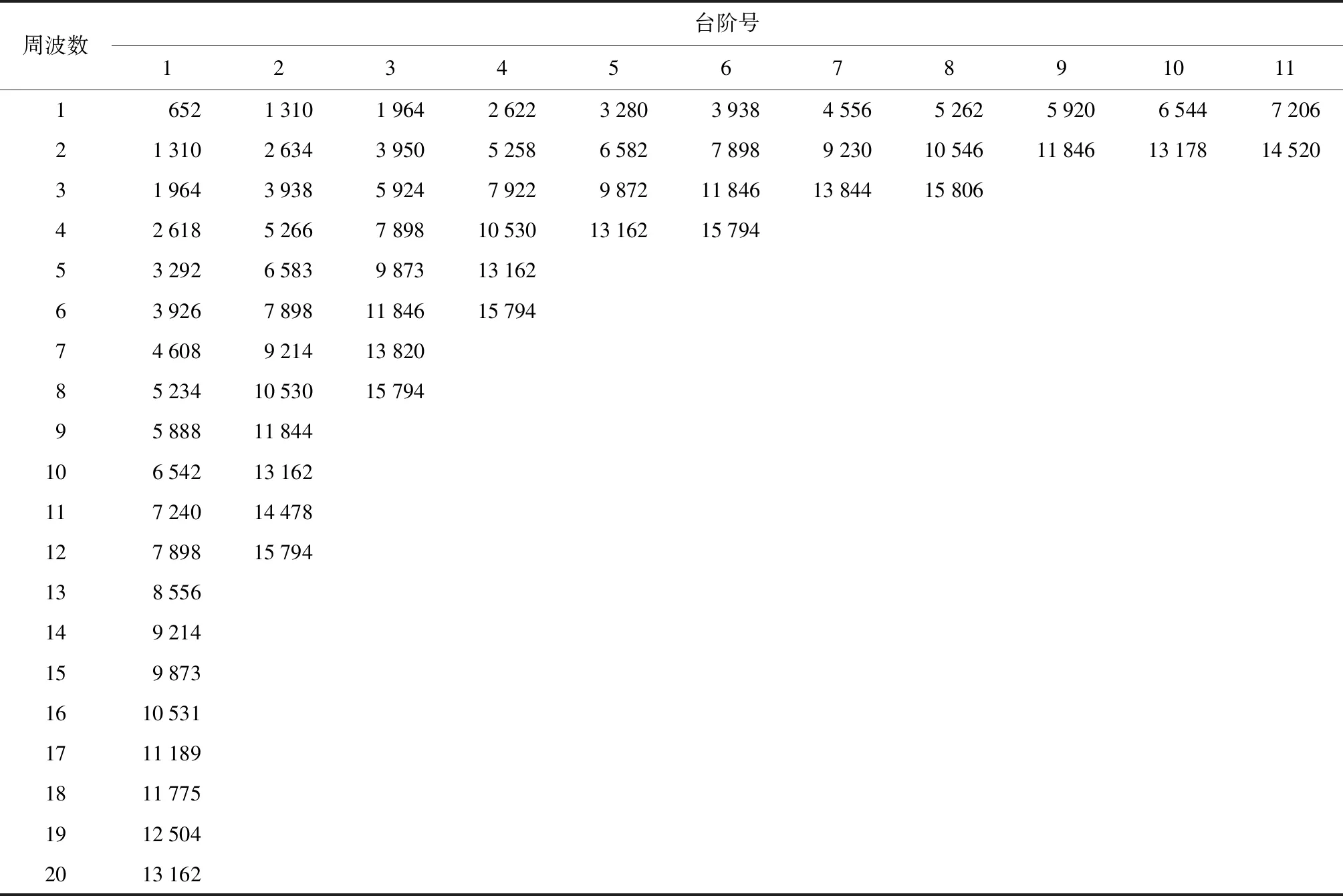
表1 相位误差台阶末端点实测表(8位A/D)Tab.1 The end point of the phase error step (8 bit A/D)
令含j个周波的序列的第i个误差台阶的末端点为ti,j,则:
j不变时,通过同周波数据ti,j的最小二乘线性拟合,得直线方程:
ti,j=G*,j×i+T*,j
(3)
i不变时,通过同台阶数据ti,j的最小二乘线性拟合,得直线方程:
ti,j=Gi,*×j+Ti,*
(4)
对上述表1中的台阶末端点数据进行同周波横向最小二乘拟合得结果如表2所示;进行同台阶纵向最小二乘拟合得结果如表3所示。

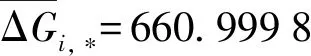

表2 第j周波不同台阶数据最小二乘拟合结果Tab.2 Least-squares fitting results of j cycles with different steps data

表3 第i台阶不同周波数据最小二乘拟合结果Tab.3 Least-squares fitting results of different cycle data for i th step
由表2和表3可见,每1个台阶内的误差规律比较均衡。即按照G*,j值判定和确认误差台阶具有合理性和客观性。
综合各个方面的因素,可以获得取整后的量子化阶梯常数为Gz:
(5)
Gz是一个核心结果,对于8位A/D而言,含j个周波的序列的量子化误差台阶宽度为Gz×j个采样点。对于含j个周波的序列的第i个量子化误差台阶末端点ti,j,有
ti,j=GZ×j×i
(6)
3.4 A/D位数变化时仿真实验结果分析
其它仿真条件保持不变,分别调整变化A/D位数分别为7、9、10 bit,获得有效位数误差特性曲线,以误差曲线台阶末端跳变峰值来寻找各级误差台阶末端点,如表4~表6所示。

表4 相位误差台阶末端点实测表(9位A/D)Tab.4 The end point of the phase error step (9 bit A/D)

表5 相位误差台阶末端点实测表(10位A/D)Tab.5 The end point of phase error step (10 bit A/D)

表6 相位误差台阶末端点实测表(7位A/D)Tab.6 The end point of phase error step (7 bit A/D)
经过与上述8位A/D情况相同的处理过程,获得如表7所述计算结果。
由表7的仿真计算结果可见,相同周波条件下,相位拟合误差随序列长度增加而呈等间隔量子化阶梯分布,依次为第1阶梯、第2阶梯等等。不同阶梯的误差界随阶梯数增高呈量子化特征下降趋势,降到一定程度后误差界趋于平稳。
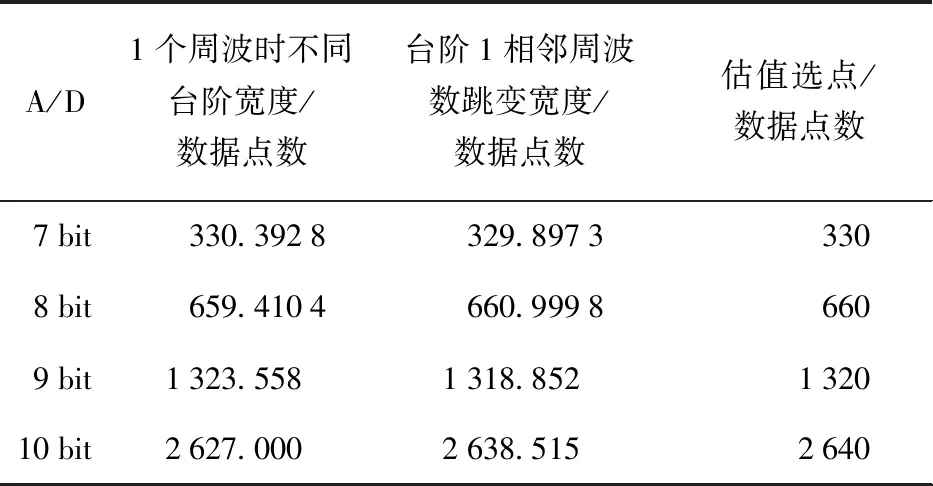
表7 相位误差阶梯参数Tab.7 The step parameters of phase error
相位拟合误差阶梯宽度与A/D位数、序列所包含的周波数等均有线性关系。
在相同A/D位数情况下,相位误差阶梯宽度与序列所包含的周波数呈线性关系;在不同A/D位数情况下,同一周波数的同一序号误差阶梯宽度与A/D位数成正比。
综合各个方面的因素,可以获得对于8位及以上位数的k位A/D而言,含j个周波的序列的台阶宽度为Gz×(k-7)×j个采样点。对于含j个周波的序列的第i个台阶末端点ti,j,k,有:
ti,j,k=Gz×(k-7)×j×i
(7)
对于8位以下位数的k位A/D而言,含j个周波的序列的台阶宽度为Gz÷(9-k)×j个采样点。对于含j个周波的序列的第i个台阶末端点ti,j,k,有:
ti,j,k=Gz÷(9-k)×j×i
(8)
式(7)、式(8)可用于估计所述测量条件下相位误差阶梯末端点位置,以便进行相位误差评定和不确定度的控制。
3.5 拓展实验
相比于相位误差规律曲线的图5,获得相同条件下频率、直流分量、幅度等参数拟合误差曲线如图6~图8所示。
从图6~图8可见,与相位误差相类似,频率误差、直流分量误差也表现出优美的等间隔量子化阶梯特征,并且它们的量子化阶梯宽度基本一致;而唯独幅度误差未能展现明显的量子化阶梯特征。
随着序列内包含的信号周波数的增加,各个参数的量子化阶梯具有展宽特征,幅度误差虽然没有量子化阶梯特征,但其误差带展宽特征与其它参数是一致的。
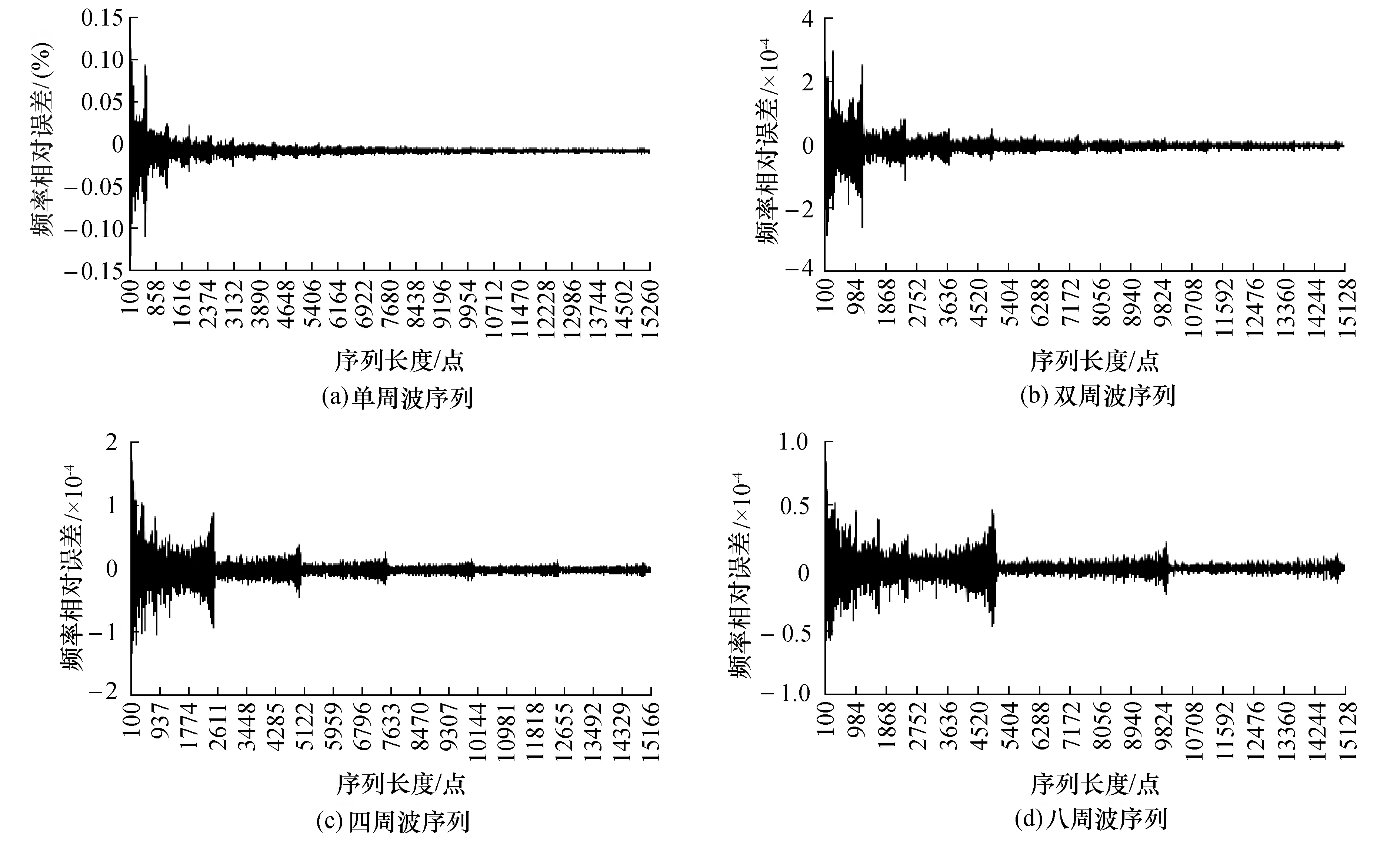
图6 频率误差随序列长度及周波变化情况Fig.6 Frequency error via data number and periods
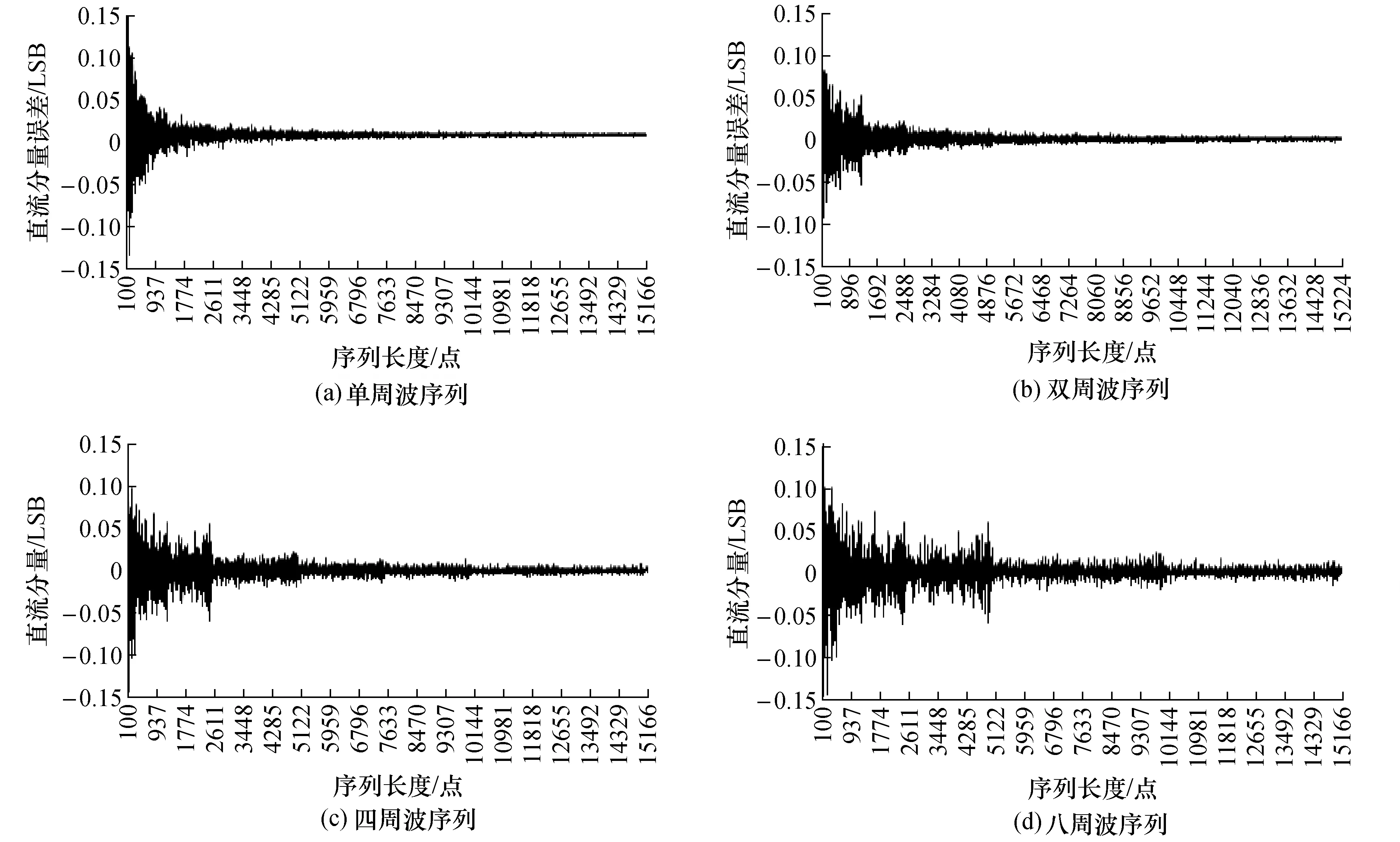
图7 直流分量误差随序列长度及周波变化情况Fig.7 Bias error via data number and periods

图8 幅度误差随序列长度及周波变化情况Fig.8 Amplitude error via data number and periods
随着序列包含信号周波数的增加,对于频率参数,量子化误差阶梯展宽的同时,伴随着误差带的缩窄,体现了两者的共同作用;对于直流分量参数,主要是量子化误差阶梯展宽,误差带的缩窄变化不明显;对于幅度参数,也体现了单调衰减的误差带的直接展宽,衰减变化特征较弱,可以按其它参数的误差阶梯规律选择测量条件。
因而,单就拟合误差而言,在其它条件相同时,序列所含的信号周波数在大于2的情况下,越小越好;周波数越少,参数拟合误差将越小。
进一步的实验研究表明,动态有效位数误差,也存在和相位误差相一致的量子化阶梯误差规律,限于篇幅,这里不再赘述。
4 机理分析及讨论
选取8 bit A/D的单周波序列拟合残差有效值与数据点数关系曲线图如图9所示。
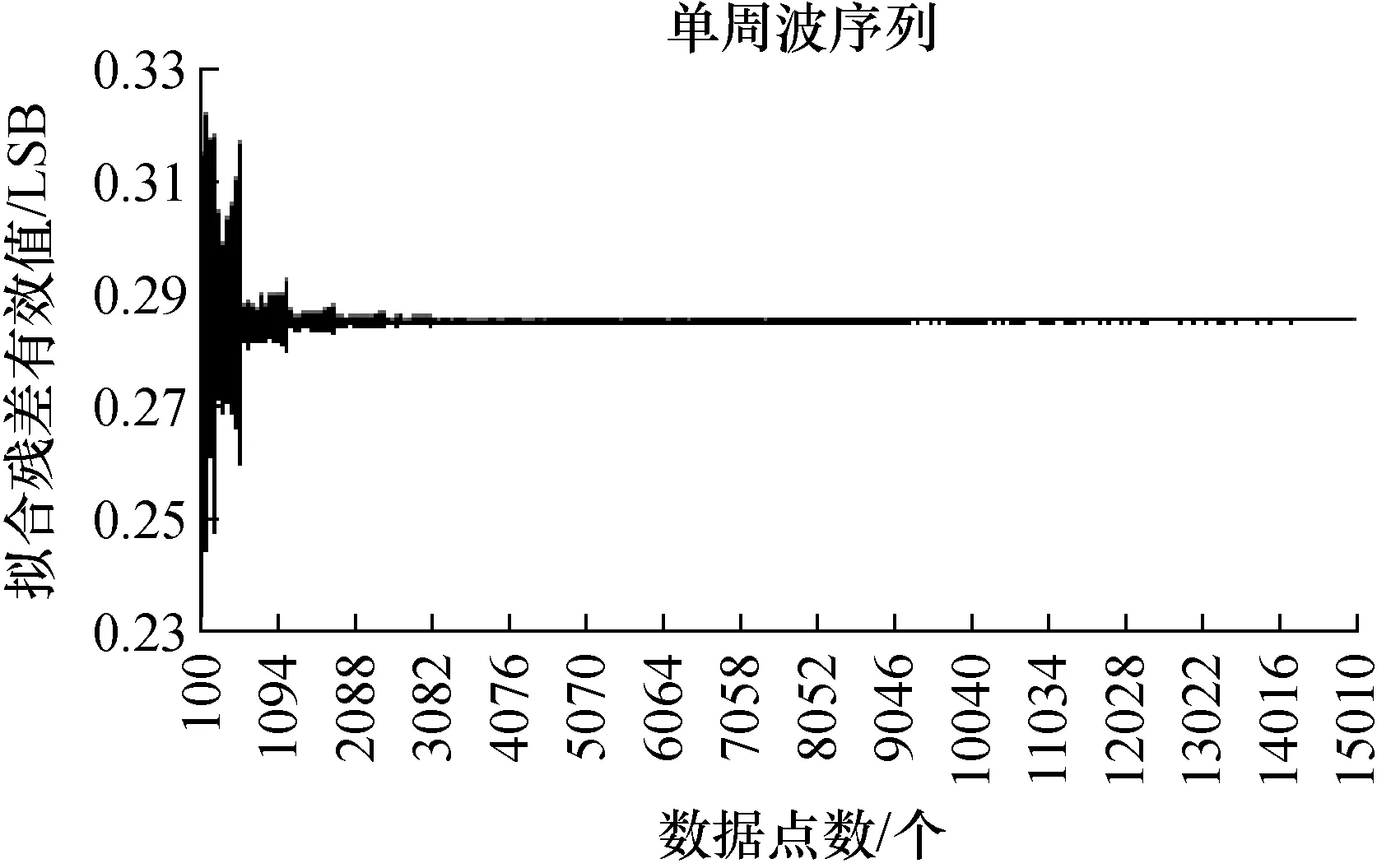
图9 单周波序列拟合残差有效值与序列点数关系Fig.9 Error of curve-fit residual via data number and periods
由图9可见,拟合残差有效值随着序列点数的增加逐渐收敛于由公式(2)所述的理论值上。其过程呈量化阶梯特征变化,并与其它正弦参数拟合误差界的变化特征和规律具有一致性。
对于等间隔采样造成的量化误差而言,它是一种具有随机性特征的系统误差,其值域特征尽管被近似为均匀分布,但由于正弦函数曲线并非是幅度等概率分布的曲线波形,因而,采样量化后的正弦波曲线,其量化误差的值域统计特征并不完全是等概率均匀分布的。
正弦波曲线各个参数拟合误差界表现出的优美的等间隔量子化阶梯特征,主要是来源于正弦波形的大周期性、采样量化造成的量化误差的局部小周期性相结合,再经过不完备的采样间隔的变化造成的误差周期性特征的一种表现形式。
当拟合序列所包含的点数较少时,其抽样后量化误差的分布与理论分布差异较大,由此导致拟合残差有效值与式(2)所述的理论值差异较大,进而使得各个拟合参数的拟合误差离散性较大,拟合参数误差界变宽。
仿真搜索表明,对于包含确定周波数的正弦采样序列拟合误差界而言,客观上存在依赖于序列点数的周期性,由此确定了其拟合误差界的量子化台阶宽度。深入分析表明,它们与序列所包含的A/D量化台阶个数密切相关,而每个A/D量化台阶范围内需要采集i·π 个点,i为正整数。
而该A/D量化台阶个数与所使用的A/D位数k、正弦波形实际所覆盖的测量范围与量程之比值η、序列所包含的周波个数j均有关系。对于含j个周波的序列的第i个量子化拟合误差阶梯末端点ti,j,k,总结出公式如下:
ti,j,k=η·i·j·2k·π
(9)
式中:0<η≤1;j为拟合序列所包含的正弦周波个数,j可以不是整数;i为正整数。
式(9)为序列长度对正弦参数拟合误差界影响的量子化阶梯边界公式。可用于估计各个测量条件下正弦拟合误差阶梯末端点位置,以便进行误差评定和不确定度的控制。
对于上述8位A/D的实验条件,k=8,η=82.031 25%,j=1,当i=1时,第1个量子化拟合误差阶梯末端点ti,j,k计算可得:
t1,1,8=0.820 312 5×1×1×28·π≈660
本文选取了A/D位数、序列长度、幅度、周波数、相位、直流分量6个条件作为仿真研究要素,以序列长度作为主变化要素,其它作为辅助变化要素,并以幅度误差、频率误差、相位误差、直流分量误差、动态有效位数误差5个变量误差作为拟合效果的指针,综合考察它们随6个条件而变化的情况。并以相位误差为事例,深入研究了其拟合误差受A/D位数、序列长度、序列包含信号的周波数影响情况,获得了一些明确的规律。
实验表明,相位、频率、直流分量、动态有效位数的估计误差随序列样本长度的变化呈阶梯状量子化跳变规律。并对阶梯宽度随样本长度、样本内所含周波数、A/D位数等要素的变化进行了定量分析,获得了上述参数估计误差界随各个因素而变化的经验公式。可用于估计任意一款A/D采样序列的正弦参数评价时的误差阶梯边界点。进而用于指导测量条件的选择和确定。
仿真结果表明,相同A/D位数条件下,含有不同周波数的正弦参数测量结果,其相同序号的误差阶梯末边界点的误差界波动较小,可认为近似相同。并且,随着A/D位数的增高而呈缓慢下降趋势。这也充分体现了误差界阶梯序号的实际意义和价值。
另外,需要说明的是,由于误差阶梯边界是使用误差峰值点识别获得的,因而,实际上若以误差界水平定义的本误差阶梯的宽度要略宽于该峰值边界点才更为合理可行。即,使用误差阶梯条件时,应尽量避免在误差阶梯边界点附近使用,应该比边界点多10%~20%的误差阶梯宽度以上使用,才可确保误差界落到下一个误差阶梯内。实际应用中应予以注意。
最后,需要特别说明的是,该结论和规律是在仅存在量化误差的仿真条件下获得的结论,没有任何随机误差因素参与其中。实际工作中,很难出现这样理想的测量状况,总会有随机因素误差出现在实际信号中,特别是小信号和微弱信号的采集测量中,随机误差可能占据主导地位。那时,本文上述结论将不再适用,但未知噪声影响是否占据主导地位的情况下,均可参照上述规律设定测量条件,将没有任何害处。
5 结 论
综上所述,本文通过大量仿真实验,对使用理想A/D转换器的仿真正弦测量序列在波形拟合中获得的正弦参数的拟合误差界进行了搜索研究,给出了出了幅度误差以外的其它参数误差界随波形周波数、数据点数、A/D位数等不同条件而呈现等间隔量子化阶梯状变化的规律,并以经验公式方式给出了其量化阶梯末端点随波形周波数、数据点数、A/D位数呈线性变化规律的估计式,以量子化阶梯宽度ti,j,k方式定量揭示出了其变化规律。
具体为,同一量子化误差阶梯内,参数拟合误差处于近似同一水平,数据点越少越好,不同量子化误差阶梯的误差界水平有显著不同,应优先选择误差界水平低的量子化误差阶梯测量条件。
该规律属于此前未被发现和定量描述的特征,对于正弦参数的精确测量及误差和不确定度控制具有重要意义和价值。

