面向大学课程时间表的并行多视图搜索算法

宋 婷，王 栋，许玉龙，王 昂

1.河南中医药大学 信息技术学院，郑州450046

2.华中师范大学 国家数字化学习工程技术研究中心，武汉430079

3.河南农业大学 信息与管理科学学院，郑州450046

随着我国高等教育的快速发展，不断扩大的教学规模和教学改革要求对如何科学集约的调配各种教学资源、合理高效地安排大学课程时间表提出了新的挑战。大学课程时间表问题（university course timetable problem，UCTP），即大学排课问题，本质上是一个具有NP难度的多约束组合优化问题[1]，这意味着不存在完整精确的快速求解算法。启发式算法通常可以在较短时间内获得一个令人满意的解，实现求解效率和质量之间的平衡。因此，设计高效的启发式算法，是求解组合优化问题的主要途径。这类算法通常可分为：直接启发式方法（包括贪婪算法[2]、图着色算法[3]等）、局部搜索算法（包括禁忌搜索[4]、模拟退火[5]等）、群智能算法（包括蜂群算法[6]、蚁群算法[7]、遗传算法[8]等）。由于该问题的复杂性，为吸引更多学者的关注和研究，学术界已举办过多次国际时间表竞赛（international timetabling competition，ITC）[9]，提供了公开的大学排课模型以便于广大研究者在同一基准下聚焦于算法与理论研究。在竞赛当中和其后的研究中，研究者往往混合多种启发式算法共同参与问题的求解，例如Müller[10]采用基于约束的混合局部搜索算法，合并爬山法、大洪水算法、模拟退火算法共同提升寻找最优解。Lyu等[4]将一种自适应禁忌搜索的混合启发式算法应用于大学课程时间表。Geiger[11]采用了一种基于阈值接受准则的随机邻域混合算法来克服求解UCTP 时的局部最优问题。Clark 等[12]应用基于修复的混合启发式搜索求解UCTP。Abdullah[13]采用基于电磁原理的混合元启发式算法对该问题进行求解，Bellio等[14]利用令牌环搜索策略混合模拟退火和动态禁忌搜索算法提升全局搜索能力，随后在另一项研究[15]中又提出对样本特征进行统计分析，从而实现参数调整的方法，包括基于特征的调整（FBT）和标准F-RACE调整等。本文作者在之前的研究[16]中也尝试了运用多类分类器指导邻域选择和参数设置，混合贪婪算法、模拟退火算法、迭代局部搜索算法共同参与求解UCTP问题。

上述算法虽然取得了一定的成果，但仍未能解决ITC 给出的所有问题实例，且之前的算法多为串行算法，在目前普遍存在的多/众核环境中，无法有效利用算力资源、发挥多/众核优势，为此本文针对UCTP 问题提出了一种全新的并行多视图搜索算法（parallel multi-view search algorithm，PMSA）。该算法运用并行计算混合多个基于模拟退火的局部搜索过程，通过视图聚合实现多视图最优解的共享与更新。在几乎没有降低迭代速度的前提下，线性扩大了搜索范围，极大地提高了全局最优解的求解质量。在对ITC基准数据集的测试中，取得了优于当前文献中的最好结果。

1 UCTP数学模型

UCTP 涉及将一组课程C={c1,c2,…,ct} 分配到不同的教室R={r1,r2,…,rm} 和时段P={p1,p2,…,pn} 中，并且要尽可能满足学校或教育机构的各种约束要求。这些约束可以分为两类：硬约束（在任何情况下都不能违反）和软约束（允许违反但应使这种违反尽可能最小）。根据时间表的一般设定，以周为单位，每天h个时段，一周d个工作日，总时段数n=d×h。这样候选解可用一个m×n的矩阵X表示，xij=ck表示课程ck分配在总课表中教室ri时段pj的位置。一般而言，满足所有硬约束的时间表是一个可行解，而同时满足所有硬约束和软约束的可行解就是全局最优解。在实际中，由于软约束之间的相互冲突，很难全部得到满足。因此，求解UCTP的目标就是在保证可行解的前提下，最小化软约束违反值。

对每一个样本I，定义集合G={g1,g2,…,gs} 是绑定了学生、教师和课次信息的课程事件集合。Cri表示涉及相同学生的课程组，CR={Cr1,Cr2,…,Crs} 表示所有课程组的集合。此外定义变量stui为课程ci所含学生数，rni为课程ci所涉及的教室数，rmi为教室ri的座位数，dni为课程ci的实际工作天数，dmi为教学计划中要求的课程ci每周最小安排的天数。最后定义二进制变量conij描述课程ci和cj是否存在学生或教师等冲突，存在冲突赋值为1，反之赋值为0。exclij描述是否允许将课程ci安排至pj时段，允许赋值为1，反之赋值为0。cpi,j描述是否允许将课程组Cri里的课程安排至pj时段，允许赋值为1，反之为0。

根据以上问题描述及变量定义，UCTP 问题的软硬约束及目标函数可数学表达如下。

1.1 硬约束及其数学表达

H1：所有教学计划中的课程事件均需分配到时间表中。

H2：时间表中任意位置仅允许分配不超过一个课程事件。

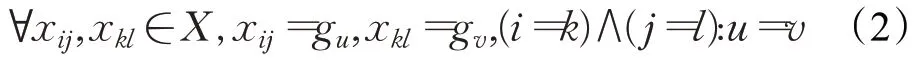
H3：任意课程事件不允许存在学生或教师等冲突。

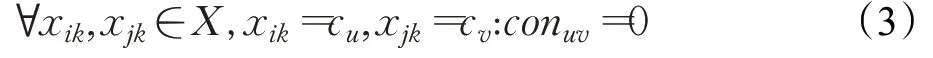
H4：任意课程不允许分配至其授课教师明确拒绝的时段。

1.2 软约束及其数学表达式

S1：任意课程的学生人数不大于所分配教室座位数。

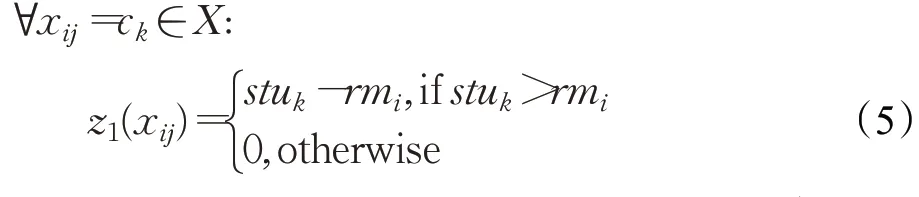
S2：同一班级的同一课程尽可能分配在同一教室。

S3：所有课程事件应满足最小工作日均匀分配。

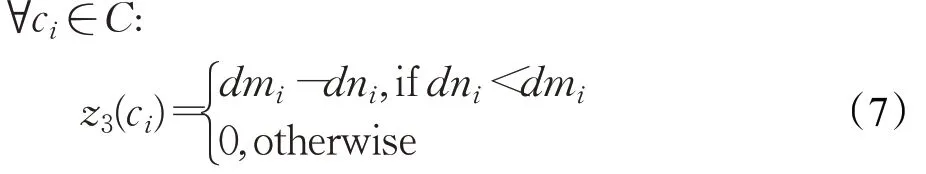
S4：同一课程组的课程应尽量紧凑分配。

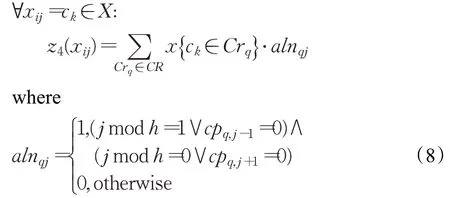
依据以上约束表达式，可以通过式（9）得到一个给定候选解X的软约束违反值。

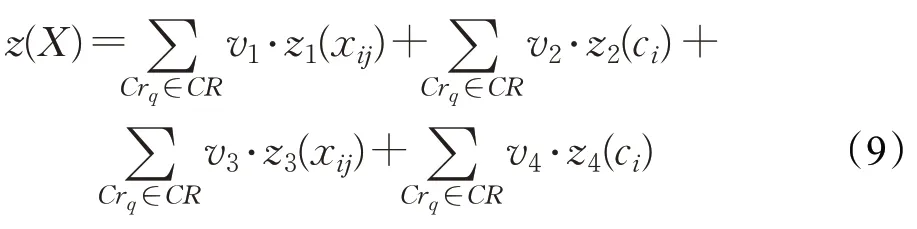
这样UCTP 问题就表示为一个在满足给定硬约束条件下，求解最小软约束违反时间表的最优化问题，即寻找可行解X*使z(X*)≤z(X)；其中v1、v2、v3、v4为每个软约束的惩罚系数。

2 并行多视图搜索求解UCTP问题

经典的迭代局部搜索算法在局部搜索算法的基础上，加入扰动算子，通过反复迭代使搜索能够跳出局部最优，具有结构简单、高效健壮的特点，在对UCTP的求解中取得了较佳的结果[17]，但也存在着迭代过程中邻域单一、耗时的缺陷。在前期工作的基础上[16-17]，本文提出一种基于改进迭代局部搜索的并行多视图搜索算法PMSA，通过对多个视图运用不同的邻域结构，使得解空间发生改变，从而增大搜索范围、跳出局部最优，并利用并行计算加快搜索速度。以下给出该算法的主要特征及实现过程。

2.1 算法主框架

PMSA 算法主要由三个阶段组成：初始解构建、多邻域局部搜索和视图聚合更新。在初始解构建阶段，仅考虑硬约束，运用贪婪启发式算法快速获取可行解作为初始解。在多邻域局部搜索阶段，先依据当前计算环境中的可用处理器数确定视图数，分别基于独立提升贡献比例构造具有不同选择概率的多邻域集。然后从前面获取的初始解出发，利用基于模拟退火的局部搜索算法并行的在多个邻域集上移动，逐步减少目标函数的软约束违反值，获取局部最优解。在视图聚合更新阶段，通过多个视图所得局部最优解的聚合，选择当前最优解作为新的初始解，并通过重新升温的扰动策略开启新一轮的多邻域局部搜索。后两个阶段反复迭代，直到达到终止条件（到达问题下界或规定时间）为止。图1 给出了PMSA算法的流程示意图。

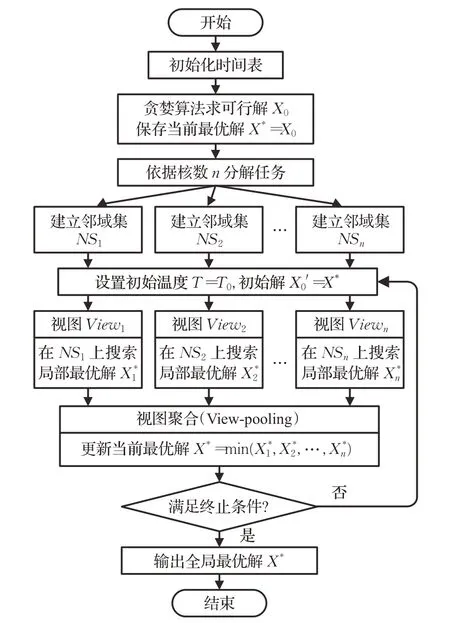
图1 PMSA算法流程示意图Fig.1 Flow chart of PMSA algorithm

可以看出，并行多视图搜索的关键在于迭代搜索的过程中，多个不同邻域状态下的局部搜索可以探索更多的方向，从而使每轮搜索都能挑选更适合问题当前状态的移动，提高了搜索效率和收敛速度。同时多个视图在相同状态下的并行搜索具有很强的并发性，极大地减少了进程间的等待时间。需要特别指出的是，尽管本文中多个视图搜索的主要差异来源于各自不同的邻域结构，但实际上也可以采用多种完全不同的搜索技术，例如引导式局部搜索[18]、禁忌搜索[4]甚至群智能方法[6-8]，当前工作仅展示了该技术的一般原型。

2.2 初始解构建

在初始解构建阶段，首先初始化一个R×P的时间表矩阵，其中R={r1,r2,…,rm} 为所有教室的集合，P={p1,p2,…,pn} 为所有时段的集合，矩阵元素为分配至该教室时段的课程。因为所有课程均已关联教师、学生，该矩阵即表示全校总课程时间表，任一教师或学生的课程时间表均可从总课程时间表里导出。

初始解的构建采用一种基于序列的快速贪婪算法：在满足所有硬约束(H1～H4)的条件下，动态地从待分配课程事件池中选择当前最难分配的课程事件，优先安排至当前被请求最少的时间表位置。课程事件的分配难度用s=ap/uc评价，其中ap为当前该课程的可选时段数，uc为该课程的剩余节次数。通过这个贪婪启发式策略，可以轻松地为本文中所有测试算例求得可行的初始解。

2.3 多邻域局部搜索

2.3.1 邻域结构

从给定的当前解X出发，通过一次邻域移动mv，可得到一个新的可行解，用X→mv表示。令M(X)为所有从X出发，在解空间中一步可达的可行移动的集合。则X的邻域可定义为：

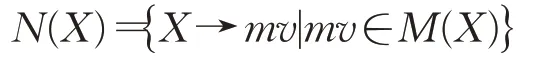
本文针对UCTP 问题的特殊性设计了两类邻域移动：随机移动和指向性移动。随机移动包含四种不同的动作，分别用时段移动、教室移动、课程交换、时段交换来表示。相应地，指向性移动也包含四个动作，分别用教室容量移动、教室稳定性移动、最小工作日移动和课程紧凑性移动表示。在这两类邻域移动中，随机移动有助于扩大搜索范围，指向性移动有助于使搜索迅速收敛到有希望的方向。两类邻域移动混合使用，能够有效提高搜索的速度和精度，具体描述如下：

M1时段移动：随机交换或移动一个课程事件到另一个可行时段。

M2教室移动：随机交换或移动一个课程事件到另一个可行教室。

M3课程交换：在确保无硬冲突的前提下，随机交换时间表中两个位置的课程。

M4时段交换：随机交换两个时段的所有课程。

M5教室容量移动：随机选择违反教室容量约束的一个课程事件，将其移动到合适的教室。

M6教室稳定性移动：随机选择违反教室稳定性约束的一个课程，将该课程所有事件交换或移动到同一教室。

M7最小工作日移动：随机选择违反最小工作日约束的一个课程，调整违反课程事件到可行工作日。

M8课程紧凑性移动：随机选择违反课程紧凑型约束的一个课程，调整违反课程事件到可行时段。

为了方便起见，将可行移动集合M1～M8表示的邻域分别定义为N1～N8。

2.3.2 候选邻域选择概率设定

局部搜索过程中，每次移动前需首先从八种候选邻域中随机挑选一种邻域作为此次搜索方向，不同的候选邻域选择概率设置决定了该邻域集搜索偏重的方向，也就造成了搜索结果的不同。现有的邻域选择概率设定方法往往是通过预先实验，设定固定的比例；或者根据问题样本的特征，确定候选邻域的选择概率。这些设定方式能够适应普通的问题样本，但是由于UCTP问题的复杂性，固定的选择比例无法匹配难度特征完全不同的算例，而依据问题样本特征在一些情况下也不能完全反映隐含的难度。例如课程组数量这一特征值并未包含每一个课程组中所涉及课程的多少和彼此之间的约束。这种隐含的关系很难通过对特征值的预先分析获得准确的度量。

受赛车比赛中的排位赛单圈成绩决定正赛发车顺序的启发，算法在正式迭代搜索之前，对每个候选邻域运行一个循环的排位赛，根据实际运行中候选邻域对总优化分值的提升贡献比设定邻域选择概率比例。具体来说，用si表示仅使用候选邻域Ni运行一个循环对软约束值得优化程度，则邻域Ni的选择概率可以用公式表示。由于基于提升贡献的邻域选择概率是从实际运行结果中得到的，有利于契合样本中隐含的特性。需要注意的是，源于算法的随机性，各视图独立运行获取的si并不完全相同，这种差异也就造成不同视图邻域搜索方向的区别，从而在客观上扩大了局部搜索范围，增大了发现全局最优解的概率。

2.3.3 改进模拟退火

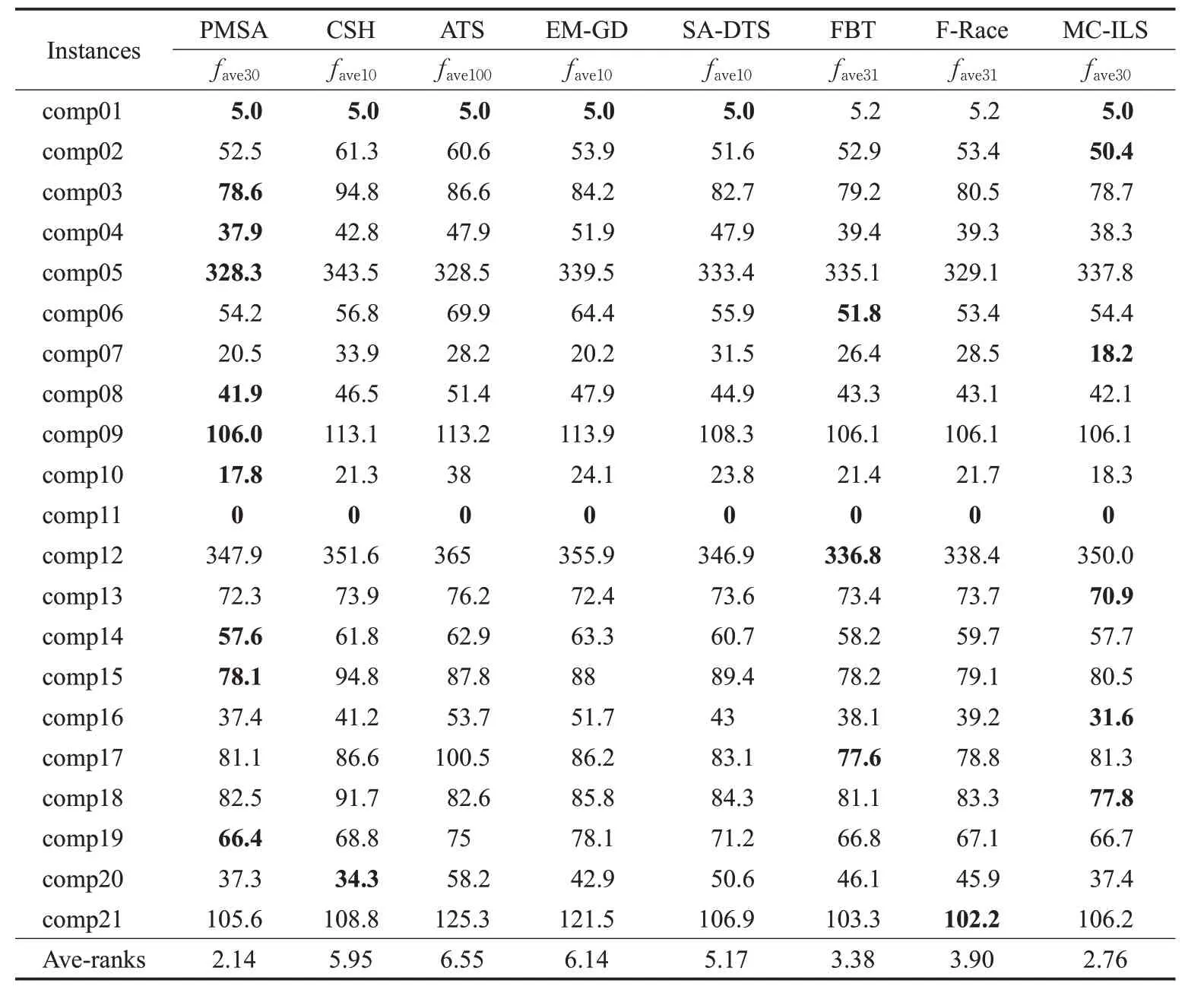
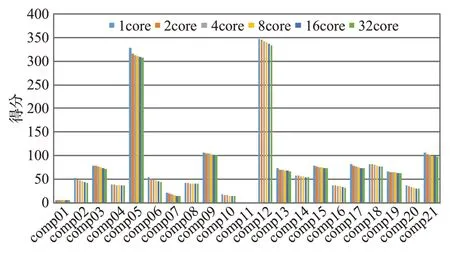
模拟退火[5]是一种经典的局部搜索算法，模拟了真实世界中固体退火的物理原理，其基本搜索过程是：先给定初始温度T，进而从初始解出发，根据特定的搜索策略在邻域中寻找新的候选解，通过判断当前解与候选解之间的差值ΔE，确定随后的动作。若候选解优于当前解，则立即更新候选解为新的当前解；反之，则按照概率exp(-ΔE/T)更新当前解。在邻域搜索的过程中，根据公式T=a×T(0

尽管模拟退火是一种易于实现的通用框架，但已被证明是处理UCTP 问题的有效方法。例如第一届国际时间表大赛的冠军、第二届国际时间表大赛中三个赛道的第一名均采用了基于模拟退火的算法。本文多视图搜索中为了提供更精确的搜索控制提高并行效率，对经典模拟退火进行改进。通过设置预定义参数Cdmax代替终止温度控制迭代次数，保证各视图局部搜索过程的同步，减少视图聚合等待时间。算法1给出了改进模拟退火过程的伪代码。

算法1 基于改进模拟退火的多邻域局部搜索

输入：初始解X0′，邻域集NS，初始温度T0。

输出：局部最优解X*。

（1）初始化当前解X、初始温度T、当前降温过程数Cd、当前恒温过程数Ct、最大降温过程迭代数Cdmax、最大恒温过程迭代数Ctmax、冷却率a、下界Zmin等基本参数。

（2）从邻域集NS中根据选择概率随机挑选一个邻域Nb，从当前解出发在邻域中寻找一个可行的候选解X′。

（3）计算候选解与当前解的差值ΔE=z(X′)-z(X)。

（4）若ΔE≤0 或rand

（5）给当前恒温过程数Ct增加1次计数。

（6）判读恒温过程数是否达到最大限制，若Ct

（7）重新初始化Ct，给Cd增加1次计数，同时降低温度T=a×T。

（8）判断是否满足迭代终止条件，若到达最大降温迭代数Cd>Cdmax或当前解分值到达下界z(X)≤Zmin，则转步骤（9）；否则，转步骤（2）。

（9）更新局部最优解X*=X，输出X*。

改进模拟退火过程涉及许多参数，其设置的有效性对算法的性能具有重要影响。在本文中，首先根据预先实验和经验设置初始温度T0及冷却率a，然后在其基础上计算设置降温过程最大迭代次数Cdmax，以保证终止温度小于0.005 且对应接受差解概率小于1×e-60。同时依据问题样本中的时段数n、房间数m以及8个基本邻域，设置最大恒温过程迭代数Ctmax≥n×m×8，以保证对时间表中所有位置移动尝试的充分覆盖。表1列出了PMSA 算法中使用的重要参数及对应的描述和配置。

表1 重要参数的设定与描述Table 1 Setting and description of important parameters

2.3.4 搜索过程的Δ计算

对当前解在不同邻域下进行移动操作，都会引起解状态的改变，相应的就要重新评估当前解与候选解状态的差距。如果每次移动都评估整体目标函数值，会消耗大量时间成本，影响算法运行效率。实际操作中，仅对移动前后的解状态进行Δ计算，且仅根据当前移动所造成的具体变化进行评估，使评估过程变得更加高效。

事实上，任何一种邻域的移动仅会引起相关教室或时段冲突值的变化。这时，只需根据当前移动所引起的相关变化进行评估即可。例如N1、N4的移动仅会引起时段的变化，N2、N5、N6的移动仅会引起教室的变化，N3、N7、N8的移动则会引起时段和教室两者的变化。

2.4 视图聚合更新

不同于一般局部搜索算法，模拟退火是一种理论上具有全局优化能力的高级过程。但由于退火时间所限，通常无法保证模拟退火一定会产生全局最优解。为进一步优化在基于模拟退火的局部搜索中获得的局部最优解，需要对当前最优解进行一定的更新和扰动后，运用迭代搜索进一步全局寻优。

与迭代局部搜索不同，PMSA算法在多邻域局部搜索阶段具有N个独立的视图（局部搜索过程），分别在具有不同选择概率的多邻域集中寻找局部最优解。在每轮局部搜索的终点，需要对N个视图的局部搜索结果进行聚合，以选择下一个迭代的初始解。显而易见由函数确定的当前具有最小约束违反值的时间表方案代表着更有希望的搜索方向，被保存为当前全局最优解，并自动更新为新一轮搜索的初始解。

在重启新一轮多邻域局部搜索之前，为跳出局部最优，需对新的初始解进行扰动。在本文采用的模拟退火过程中，通过重新设置初始温度T0以达到扰动目的。具体重启次数iter依据终止时间限制和单次搜索时间的比例设置。

3 实验与分析

3.1 测试算例与实验设定

为了验证PMSA算法的有效性，本文对第二届国际时间表大赛的UCTP 问题（ITC-2007 track3）进行实验验证。大赛规定及相关细节可参考[19]。该数据集包含21个源自真实世界的基准测试算例。相对于竞赛中要求比较算法在不同随机种子下独立求解10次的平均结果，后续研究考虑到计算的随机性，为增强比较的公正程度，采用了更多次数（30～100）的平均结果进行算法评价，本文在相关实验中也采取相同的设定。PMSA 算法采用C++编写，并在配备Intel E5 2.6 GHz CPU 和32G RAM 的服务器上进行了测试。执行时间基于ITC-2007 规则，这是用基准工具确定的时间限制，运行环境中为208 s。

3.2 ITC-2007竞赛规则下的对比实验

实验首先在ITC-2007 竞赛规则下，比较了PMSA（仅使用单核状态下）与文献中七种最先进的UCTP 问题求解算法的性能差异。这七种算法包括在竞赛中获得前两名的Müller提出的CSH[10]和Lyu等提出的ATS[4]，赛后最新研究中Abdullah 等提出的EM-GD[13]，Bellio 等提出的SA-DTS[14]和后续提出的FBT 和F-Race[15]，以及作者之前提出的MC-ILS[16]。考虑到比较的公平性，实验采用与最新研究FBT 和F-Race 相似的运行次数，对每个实例独立运行30次取平均值。获得的结果分值越低，该算法的能力越强。表2给出了PMSA算法和其他七种参考算法在UCTP问题的21个算例上的运行结果。

如表2所示，PMSA算法在全部21个算例中获得了11个最佳平均结果（每个算例的最佳平均结果以粗体显示），相对于其他最新算法，PMSA显示出明显优势。最后一行给出Friedman 非参数统计检验的Average ranks分值也得出了相同的结论。在仅使用单核处理器的情况下，PMSA 退化成为与MC-ILS 类似的迭代局部搜索算法，但依赖于八候选邻域设计及新的候选邻域选择概率设定规则，仍然在整体精度上取得一定的提高，显示了所提策略的有效性。

表2 ITC-2007竞赛规则下的平均得分对比Table 2 Comparison of average scores under ITC-2007 rules

3.3 并行多视图搜索对比实验

在随后的并行多视图搜索测试中，分别比较了在PMSA算法分别在1核、2核、4核、8核、16核、32核CPU参与的情况下，对算法性能的提升。实验终止条件仍然采用ITC-2007 竞赛所定的基准时间。图2 给出了针对UCTP问题21个算例，在不同的并行条件下取得平均分值的对比结果。

图2 不同并行条件下的平均分值Fig.2 Average scores under different parallel conditions

从图2 可以看出，在相同的基准时间下，随着更多处理器参与计算，在除comp01和comp11两个已到达下界的简单算例之外的所有算例中都取得了线性的提升，多视图聚合相对于单视图的迭代局部搜索在收敛速度和搜索能力上显示出明显优势。

在并行多视图搜索当中，多个由不同选择概率设定构造的多邻域结构，使得算法在提升对重点区域搜索深度的同时，也扩大了邻域搜索范围，本质上是以更多的计算为代价换取精度上的提升。在给定时间限制条件下，借助并行计算有效利用已有计算资源是一种简单易行的方案。多个独立局部搜索过程具有显著的并行性，最大程度保证各局部搜索过程的同步，减少视图聚合等待时间，是提高并行效率的关键。通过对模拟退火算法改进，用预定义参数代替终止温度控制循环次数，使每个视图中搜索次数均为Cdmax×Cdmax，保证了局部搜索结束时间基本一致。在16 核以下的实验中，视图聚合更新的迭代次数与仅单核参与的迭代次数完全相同，仅在32核的实验中，个别算例视图更新次数有少量下降，表现出良好的并行能力。

4 结束语

本文对大学课程时间表问题（UCTP）进行了研究，提出一种全新的并行多视图搜索算法。该方法通过包含八种基础邻域的多邻域设计，根据实际运行中候选邻域对总优化分值的提升贡献比设定邻域选择概率比例，有效提升了局部搜索效率；并利用多视图学习策略融合多个并行局部搜索过程结果，及时修正搜索方向，显著提高了算法的收敛速度和搜索能力。在著名的包含21个问题实例的UCTP 基准数据集上进行的对比实验表明，与当前文献中表现最佳的七种启发式算法相比，在ITC-2007竞赛终止条件下PMSA获得了最多的11个实例的最好结果；在并行多视图搜索对比实验中更体现出在多/众核环境下更强的求解精度和搜索潜力。在未来的工作中，将对多视图搜索阶段运用不同的局部搜索算法或群智能算法做进一步研究，同时可尝试将PMSA应用于时间表领域的其他复杂组合优化问题。