基于GA-BP神经网络的深基坑变形最优化预测研究

邱章龙

(中铁七局集团武汉工程有限公司，湖北 武汉 430000)

1 概述

随着我国经济发展水平不断提高，基础设施建设更新需求日益增加，高速公路作为我国公共交通基础设施的重要一环，国民经济发展上发挥着至关重要的作用。由于城市地上空间的制约，地下空间的拓展利用逐渐增多，城区复杂环境下明挖隧道施工技术趋于成熟，与此同时深基坑施工技术也得到愈加广泛的应用，传统基坑监测方法忽视地下水位的预警，错失解决问题的良机，因此造成重大安全问题。地下水位随时间呈不规则非线性变化，具有优越的非线性动态处理能力的BP神经网络被广泛用于预测。目前，不少研究人员依托实际工程构建了多种BP神经网络模型用于工程预测。季慧等[1]运用了一个基于混沌的局部搜索技术大大提高了算法收敛速度；刘海龙等[2]利用遗传算法对BP神经网络进行改进操作，提高了模型的稳定性和预测能力；黄震等[3]构建了基于模拟退火法的SA-BP神经网络预测模型对软土基坑开挖墙后最大地表沉降进行预测，并进行了对比和验证；谢饶青等[4]提出一种基于NPCA-GA-BP神经网络预测方法提高了采场稳定性；刘蕊蕊等[5]通过遗传算法和拉文伯格-马尔夸特算法改善了BP算法收敛速度慢，易收敛到局部极小点的问题。

为了提高工程进展的高效性和稳定性，本文依托广州新白云国际机场第二高速公路南段工程新塘互通立交路段大观路隧道工程，就城区复杂环境下明挖隧道深基坑开挖过程中土体及地下水位监测数据展开预测优化研究。通过实时监测数据进行分析，结合城市轨道交通工程监测技术规范，提出工程优化策略，实现科学、优质、安全、高效的现代项目管理。

2 工程概况

2.1 工程基本情况

工程主体为总长度1 520 m的明挖隧道，隧道于天河区大观中路新园新村附近起始，终点位于广深高速公路广氮收费站，里程范围从K44-240到K44-280，其中地下暗埋长度945 m，地面敞开长度575 m。大观路隧道平面图如图1所示。

2.2 地质条件

施工现场钻探结果显示：地质从上到下依次为全新统人工填土层、全新统河流相冲积层、上更新统河流相冲积层及残积层。

其中，全新统人工填土层包含部分地段呈层状分布的褐灰色杂填土以及大部分地段呈层状分布黏性土；全新统河流相冲积层主要包含场区部分地段的呈似层状分布的粉质黏土，绝大部分地段的呈层状连续分布的粉质黏土；冲积层揭露于场区大部分地段的呈层状粉质黏土和场区部分地段的呈似层状分布的粉质黏土；残积层裸露于场区部分地段的呈透镜状分布的可塑状砂质黏性土以及呈层状分布的砂质黏性土。

2.3 气候条件

施工现场所属地区为亚热带季风气候，全年降雨量十分充沛，夏季炎热，冬季温暖。第二、三季度受洋流影响，以偏南风、天气炎热、降雨量大为主要特征。

2.4 监测方案

施工工程中实际位移越大，风险系数越高，因此将位移较大点位设为风险点位进行监测，同一点位布置1个～3个监测点，同时进行地下水位监测、桩顶沉降及水平位移监测，监测点位置距离基坑侧面6 m，基坑断面图如图2所示。其中桩(墙)顶沉降监测、桩(墙)顶水平位移监测、地下水位各3个测点，监测点位示意图如图3所示。

2.5 现场实测

本文主要在已开挖的里程范围段关键点位进行了桩顶沉降及水平位移、桩体深层水平位移、地下水位、立柱结构竖向位移的监测工作，本次监测时间从2021年9月1日持续至2022年2月23日，其中地下水位、桩(墙)顶竖向位移、水平位移初始数据由勘察报告得出。图4,图5为数据监测传感器安装现场。

2.6 现场监测数据分析

施工过程监测点数据保持稳定，附近支撑轴力测点最大累计变化值为1 469.30 kN，地下水位测点最大累计变化值为-0.80 m，地下水位测点最大累计变化值为-17.7 mm，桩体深层水平位移测点最大变化值为20.84 mm，支护桩(墙)顶部竖向位移测点最大变化值为-19.30 mm，支护顶部水平位移测点最大变化值为23.19 mm，立柱结构竖向位移最大变化值-13.70 mm，累计变化值均在控制值范围内，风险可控。

从现场监测数据分析来看，每个监测点的数据都有相似的规律性，不同的因素对地下水位影响程度如图6，图7所示。随着墙体水平位移增大，地下水位值也逐渐增大，变化曲线从陡峭向平缓过渡，随着立柱结构竖向位移增大，地下水位值逐渐减小，曲线曲率变化小。

支护桩(墙)顶部竖向位移增大时，地下水位值呈现先减小后增大的变化趋势，且减小段曲率较大增大段曲线较为平缓，支护桩(墙)顶部水平位移与地下水位值呈反比关系。

总体来看，地下水位与立柱结构竖向位移、墙体水平位移、支护桩(墙)顶部竖向位移、支护桩(墙)顶部水平位移表现出紧密的关联性和规律性，而且呈现非线性变化。每一个变量都有合适值，偏离合适值有可能产生不良后果，例如地下水位过高，会引起浅基础地基承载力的降低，岩土体在部分地区例如有的地震砂土地区易产生变形、崩塌等严重地质灾害；地下水位过低，容易导致周边道路、建筑物等沉降不均而倾斜、坍塌等等，因此，有必要对地下水位值进行优化预测[6]。

3 GA-BP神经网络

BP神经网络包括输入层、隐含层、输出层，BP神经网络正向传播过程中，输入层输入信号后，隐含层对信号逐层处理再从输出层输出，当结果与期望值存在较大偏差时，误差信号沿原通道反向传播，在不断调整各层神经元的权阈值方法下，输出误差信号不断减至最小，信号单向传递时下一层状态只受上一层影响。所以BP神经网络利用误差反向传播训练前馈网络，系统地解决了多层中隐含单元连接权的学习问题。本文选取该施工项目监测数据中与地下水位相关的立柱结构竖向位移、墙体水平位移、支护桩(墙)顶部竖向位移、支护桩(墙)顶部水平位移4个数据作为输入量，地下水位值作为输出量，单层隐含量节点为7，BP神经网络结构如图8所示。

BP神经网络简单实用，执行效率高，具有强大的自适应能力，无论是在理论分析还是在实际的应用方面都比较成熟，但是依然存在网络收敛速度慢和容易陷入局部极小值的不足[7]。因此，为了实现更好的预测效果需要引入遗传算法(GA)进行改善[8]，遗传算法(GA)属于一种生物智能算法，通过借鉴生物染色体交叉变异保留优良个体的特性，不断筛选优化BP神经网络的权值和阈值，极大地减小了输出误差，提高算法稳定性。BP神经网络算法流程以及GA算法的优化过程如图9所示。

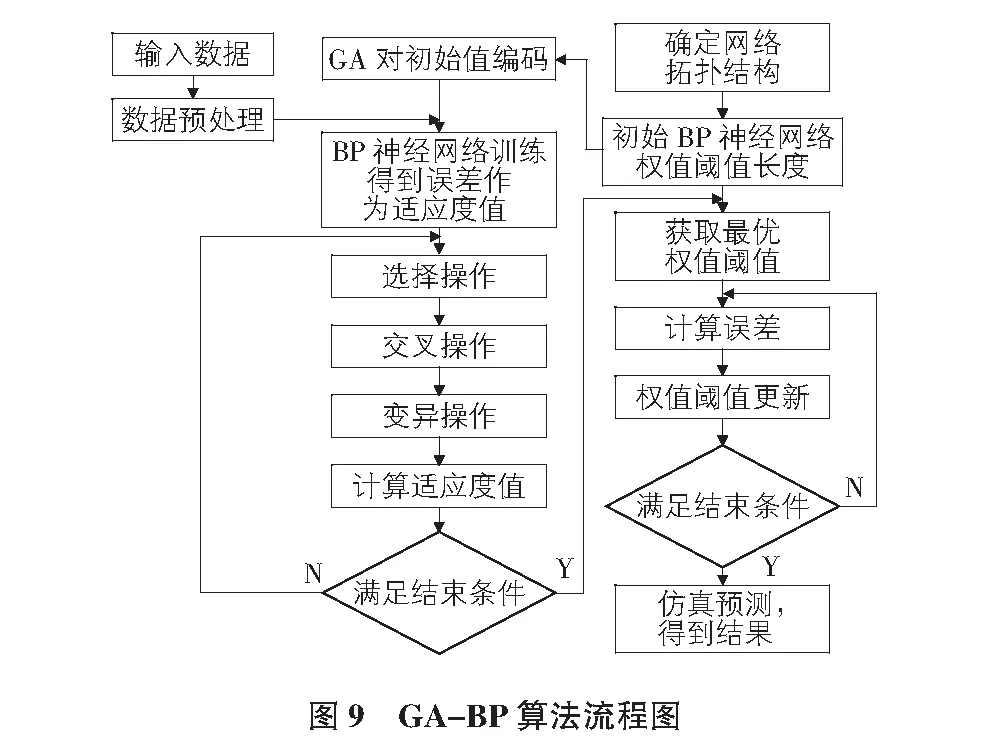
3.1 基于GA-BP神经网络算法的预测优化算法应用

实验步骤如下：

1)选取K44-280段监测点1右端的实测数据为样本，将数据导入MATLAB并做归一化处理，设置变量的取值范围和染色体长度。

2)利用BP神经网络的自适应性以及误差负反向传播特性，可采用遗传算法优化BP神经网络的权值和阈值，采用适应度为优化评价标准，适应度为BP神经网络输出值的绝对误差累加响应，适应度值越低，代表网络权值和阈值最优，收敛效果越好[9-11]。

3)在得到最优的权值和阈值后设定BP神经网络参数，对样本数据进行神经网络训练，得到一系列训练结果。

4)预测误差过程必不可少，主要是将检测数据输入然后进行模拟输出，得出相应结果；选取其中立柱结构竖向位移、墙体水平位移、支护桩(墙)顶部竖向位移、支护桩(墙)顶部水平位移和最小的一组结果作为目标最优值。输入层、隐含层、输出层的参数设置如表1所示。

表1 网络训练参数

优化后形成的模型适应度曲线变化趋势见图10，平均适应度曲线呈阶梯形快速下降，在反复对模型进行遗传优化后，个体适应度指标逐渐下降、适应力不断增强，在进化到第5代时，适应度数值趋于稳定。

图11的训练回归图印证了输入量和输出量之间极大的相关性，在70%的训练部分相关系数达到0.996 41，15%验证相关系数为0.980 61，剩下15%的测试部分相关系数也有0.963 28，总体相关系数值为0.974 08，神经网络训练效果优异，为接下来的预测优化奠定基础。

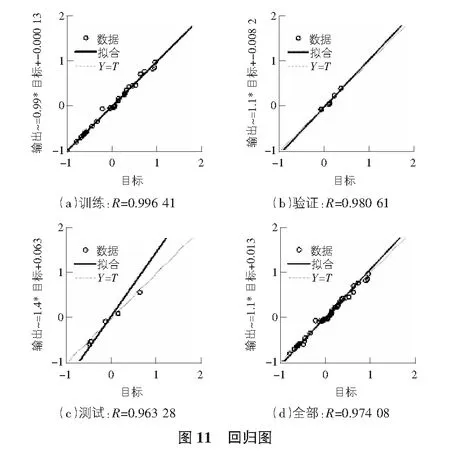
给每一个变量设置范围，使范围同时处在安全值和实测数据之内，采用循环计算的方法，将所有可能的组合输入到经过训练的GA-BP神经网络中，以变量相加得到最小值为最优结果，以此寻找最优地下水位值及其条件。

对神经网络进行全域搜索，得到的预测值如图12所示，预测信号和原始信号趋势基本吻合，经过遗传算法优化的BP神经网络得出的K44-280监测点1(右)最优地下水位值为3.852 7 m，达到此最优数值时的条件为立柱结构竖向位移9.1 mm，墙体水平位移2.5 mm，支护桩(墙)顶部竖向位移3.10 mm，支护桩(墙)顶部水平位移19.0 mm，以上数值均在安全范围内。

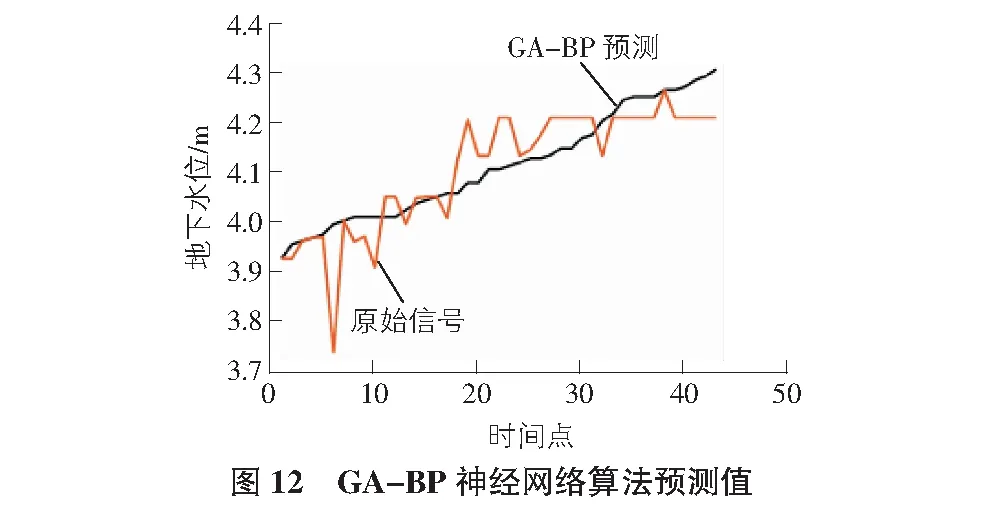
误差曲线如图12所示，对比多元回归方程预测的数值误差图如图13,表2所示。

表2 误差对比

由图13可知，基于遗传算法的BP神经网络算法具有良好的误差控制能力，误差曲线锯齿状延伸，整体误差在±0.1范围内波动，曲线多元回归分析曲线在前40 min也呈现良好的误差表现，变化趋势与GA-BP神经网络算法大致相同，误差震动幅度稍大，峰值超过0.25。

绝对误差代表了测量值与真实值之间的偏离程度，均方误差则是度量估计量和被估计量之间的差异程度的值。由表2可知，GA-BP神经网络算法的绝对误差均值和误差均方差均小于多元回归分析方法，体现了机器学习方法在数据分析上的优势。

3.2 实验分析及建议

实测数据表明立柱结构竖向位移、墙体水平位移、支护桩(墙)顶部竖向位移、支护桩(墙)顶部水平位移、地下水位之间有良好的相关性，基于遗传算法优化的BP神经网络算法能够精确预测地下水位最优值，实验误差略高于目标误差，但误差控制总体处于优良状态，不影响实验准确程度，而且通过误差对比得出相比于多元回归分析，采用遗传算法优化的BP神经网络算法预测效果更好，预测结果更平滑。建议在后续的施工过程中，充分利用神经网络，深度学习方法，结合施工现场数据，进行更全面、误差更小的数据分析工作，为后续工程的平稳、安全、高效地向前推进提供数据支撑和保障。

4 结语

本文通过GA-BP神经网络算法部分的理论分析及基于现场数据的分析仿真实验，对明挖法市政隧道深基坑过程中的现场数据进行了详细的分析和预测，并针对后续施工给出了优化意见。研究结论表明：

1)监测数据之间相互影响且影响程度各不相同，其中地下水位与立柱结构竖向位移、墙体水平位移地下水位、支护桩(墙)顶部竖向位移、支护桩(墙)顶部水平位移之间呈现极大相关的非线性变化规律。

2)机器学习方法能够精确预测地下水位最优值及达到最优时的条件，本文运用基于遗传算法的BP神经网络法对地下水位进行预测分析，得到最优结果绝对值为3.852 73 m，此时条件为：立柱结构竖向位移9.1 mm，墙体水平位移2.5 mm，支护桩(墙)顶部竖向位移3.10 mm，支护桩(墙)顶部水平位移19.0 mm，根据城市轨道交通工程监测技术规范[11]，均处于安全范围内。

3)通过误差对比，揭示了GA-BP神经网络相比传统多元回归分析方法具有更好的预测能力和误差控制能力，展现了机器学习在工程应用上的独特优势。