改进西原蠕变模型研究及二次开发计算*

王宝迪，宿利平，刘 洋

(1.北京科技大学 土木与资源工程学院，北京 100083；2.北京市政路桥股份有限公司，北京 100045)

0 引言

流变是岩土体重要的力学特征之一，包括蠕变、应力松弛、长期强度等现象[1-2]。软黏土具有明显的时效性,其蠕变特性导致大量工程出现严重的工后沉降问题，如建筑物的下沉及破坏、城市给水及供气等市政设施无法正常运行、路面高低不平影响交通运输等。软土本构模型的选取是合理预测软黏土沉降的关键。目前，关于岩土体蠕变的研究已取得一定成果，其中，经验模型和元件模型为目前运用最广泛的蠕变本构模型[3]。经验模型具有表达式简单、模型参数易获取和运用方便等特点。目前已有不少国内外学者基于大量试验，应用经验模型研究不同应力水平下软土蠕变特性[4-7]。但其研究成果主要基于三轴蠕变试验对不同应力水平下蠕变曲线进行研究，选用某种特定的函数形式与蠕变曲线对比分析，而未对不同函数形式的经验蠕变模型进行分析评价。

常用的元件模型有Kelvin模型、Merchant模型及西原模型等。其中传统西原模型在三参量模型H-K的基础上串联了黏塑性元件，能较好地模拟岩土的流变特征。一些学者为了更准确地描述岩土体流变规律，在传统西原模型上作出改进[8-11]。以上研究成果主要对经典元件模型做修正，从而改进模型在描述岩土体流变阶段中的不足，研究对象多为岩体，而对于软土的研究相对较少。

本文基于经验模型的研究提出幂函数非线性元件，并在经典西原模型基础上进行改进，提出改进西原蠕变模型。根据试验结果[12-13]研究经典西原模型与改进西原模型描述不同应力状态下的准确度及参数敏感性，基于有限元软件ABAQUS平台对改进西原蠕变模型进行二次开发，建立数值模型，将程序模拟值与试验值进行对比，验证本文建立的改进西原模型及子程序的适用性及有效性。改进西原模型及相关二次开发可对软黏土路基进行快速、准确的沉降预测，以保证对软土工程设计、施工、加固、灾害预防和防治全工程周期提出合理化建议以达到工程安全生产及运行的目的，为软土的沉降计算提供新的途径和方法。

1 经验蠕变模型

1.1 3种常用的经验蠕变模型

常用的经验模型有幂函数模型，对数型模型和指数型模型等，其基本表达式如下：

1)幂函数模型

幂函数模型的基本形式可以写成如式(1)～(2)所示：

ε(t)=a+btc

(1)

ε(t)=a[(1+bt)c+1]

(2)

式中：a,b,c是经验常数。

2)对数模型

对数模型的基本形式可以写成如式(3)～(5)所示：

ε(t)=a+bln(t+c)+dt

(3)

ε(t)=bln(1+ct)

(4)

ε(t)=a+bln(t+c)

(5)

式中：a,b,c,d是经验常数。

3)指数模型

指数模型的基本形式可以写成如式(6)～(8)所示：

ε(t)=A(1-be-ct)

(6)

ε(t)=a+A(1-e-ct)

(7)

ε(t)=a+A(1-be-ct)

(8)

式中：a,b,c,A是经验常数。

1.2 拟合结果分析

根据以上模型，选取成都黏土蠕变试验结果[12]作为参数拟合的参照样本，使用最小二乘法对上述8个模型进行参数拟合，本文以基准指数决定系数(R2)用于评估上述8个模型的性能，如式(9)所示：

(9)

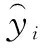
从表1～2可知，对于轴压为83.49 kPa的蠕变曲线，对数模型的式(4)的决定系数最高，拟合度最好，但对于高轴压333.96 kPa的决定系数仅为0.039 5，不适合应用于高应力水平的蠕变曲线计算；对于轴压为333.96 kPa的蠕变曲线，对数模型的式(5)的决定系数最高，拟合度最好，但对于低轴压83.49 kPa的蠕变曲线无法得到曲线拟合结果，不适合应用于低应力水平的蠕变曲线计算。

表1 轴压为83.49 kPa时3种经验蠕变模型的比较结果Table 1 Comparison results of three empirical creep models when the axial pressure is 83.49 kPa

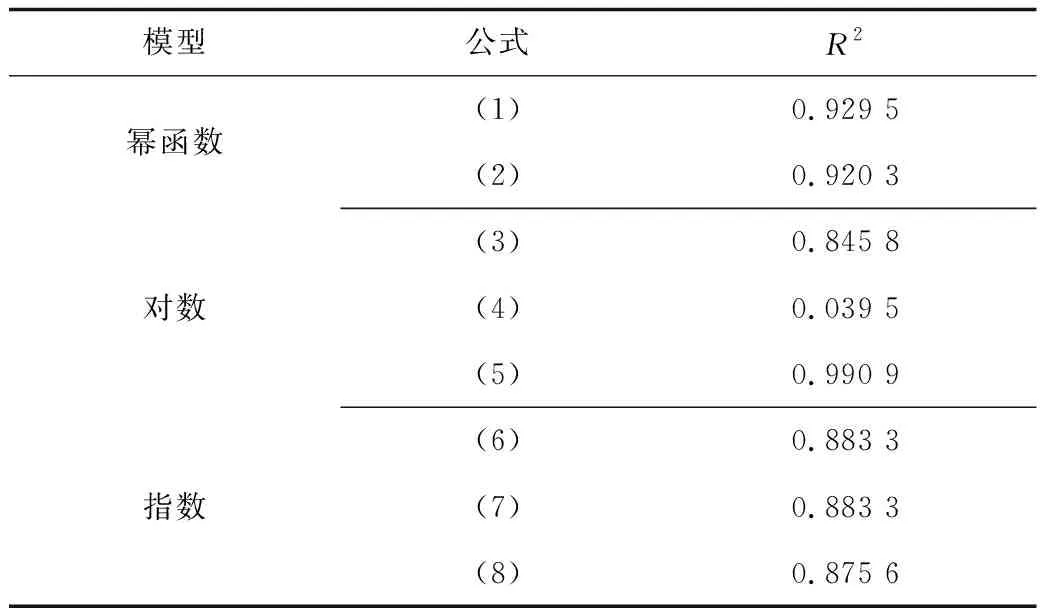
表2 轴压为333.96 kPa时3种经验蠕变模型的比较结果Table 2 Comparison results of three empirical creep models when the axial pressure is 333.96 kPa

幂函数模型和指数模型在轴压为83.49 kPa下的拟合度差别较小，且都能大于0.90以上；而对于轴压为333.96 kPa蠕变曲线，幂函数模型的拟合度大于0.90，明显优于指数模型的拟合度。

综上所述，对数模型虽然在低应力水平和高应力水平下都有最高的拟合度，但分别对于另1种应力水平的拟合度较差；幂函数模型在低应力水平的拟合度与指数模型的拟合度相近，但在高应力水平下，拟合度明显优于指数函数的拟合度。

1.3 幂函数非线性元件

幂函数经验模型对黏土的三轴蠕变曲线在低应力水平下和高应力水平下都有着较高的拟合度。本文在幂函数经验模型的基础上，提出幂函数非线性元件，如图1所示，其本构如式(10)所示：

(10)

式中：Em′为幂函数元件简化前的初始弹性模量；a′，b′，c′为幂函数元件简化前的计算参数。

图1 幂函数非线性元件Fig.1 Power function nonlinear element

这里假设a′不为0，故幂函数非线性元件本构可化简为如式(11)～(12)所示：

(11)

(12)

式中：Em为幂函数非线性弹性模量；E0为初始弹性模量；b，c为幂函数非线性元件的计算参数。

2 改进西原蠕变模型

2.1 传统一维西原蠕变模型

西原模型由1个Hooke体、1个Kelvin体和1个非线性Bingham体串联而成。如图2所示。

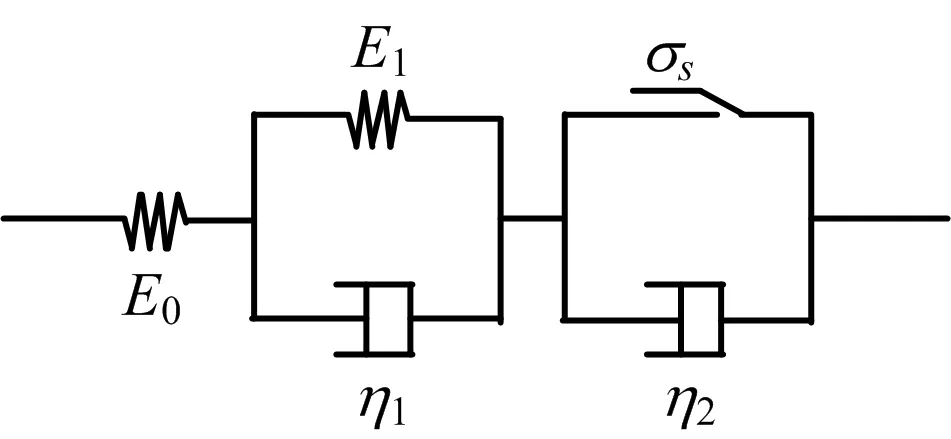
图2 经典西原蠕变模型Fig.2 Classic Nishihara Creep Model

Hooke体能够描述土体在外力作用下的瞬时变形；Kelvin体将1个Hooke体和1个黏壶元件并联，能够描述土体在外力作用下的黏弹性变形；非线性Bingham体能够描述土体在外力作用下达到屈服应力所产生的黏塑性变形。一维西原模型蠕变本构方程如式(13)所示：

(13)

式中：E0为Hooke体的弹性模量；E1，η1分别为Kelvin体的弹性模量和黏滞系数；σs，η2分别为Bingham体的屈服应力和黏滞系数。定义如式(14)所示：

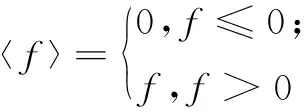
(14)

2.2 改进西原蠕变模型

传统的西原模型被广泛应用于描述岩土材料的蠕变特性，能够描述衰减和稳态蠕变过程，但不能较准确地反映加速蠕变并且对非线性性质的描述还存在不足。为了较清楚地描述不同应力水平下黏土蠕变全过程，本文在原始西原模型的基础上应用上文提出的幂函数非线性元件替换西原模型原有的弹性元件，并引入非线性黏塑性体(NVPB)模型[14]构成改进的西原模型，其模型结构示意图如图3所示。

图3 改进西原蠕变模型Fig.3 Modified Nishihara creep model

NVPB模型由1个塑性开关和非线性黏性元件并联组成，在恒力σ0下的蠕变方程如式(15)所示：

(15)

式中：ε为在软土应力σ下的应变量；ηm为NVPB体黏性系数；t为蠕变总时间；t0为参考时间。改进的一维西原模型蠕变本构方程如式(16)所示：

(16)

2.3 改进西原模型蠕变参数敏感性分析

在应力状态相同的条件下，对式(16)的待定系数b，c，n进行敏感性分析。图4(a)～图4(c)分别为系数b，c，n对改进西原模型蠕变曲线的影响。图4(a)可以看出b的变化对土体初始瞬时应变大小影响较为显著，而对蠕变曲线的最终总应变量影响较小，b的值越大蠕变曲线的初始应变值越大。图4(b)可以看出c的变化主要影响蠕变曲线的最终总应变量，当c值减小并小于零时，蠕变曲线应变值明显增大，当c值增大并大于零时，蠕变曲线可以描述土体的负蠕变现象。图4(c)可以看出n的取值对蠕变曲线所反映的蠕变变形有着显著影响：当n≤1时，蠕变曲线可描述黏土瞬时弹性变形和衰减蠕变变形；当n>1时，蠕变速率逐渐增加，且n越大，蠕变速率越大。

图4 蠕变参数对改进西原模型蠕变曲线的影响Fig.4 The influence of creep parameters on the creep curve of the improved Nishihara model

2.4 改进西原模型适用性验证

为验证本模型的精度和适用性，选取成都黏土[12]蠕变试验结果作为参数拟合的参照样本，该文献以成都黏土作为研究对象进行不同应力下的三轴蠕变试验，软土在低应力条件下(轴向应力为83.49，166.98，250.47 kPa)其中变形经过瞬时蠕变和衰减蠕变后趋于稳定，而在高应力条件下(轴向应力为333.96 kPa)，蠕变变形最终进入加速蠕变而使土体发生破坏。本文采用成都黏土试验蠕变结果对经典西原模型及改进的西原模型进行拟合分析，拟合得到的计算参数见表3～4，拟合曲线见图5。

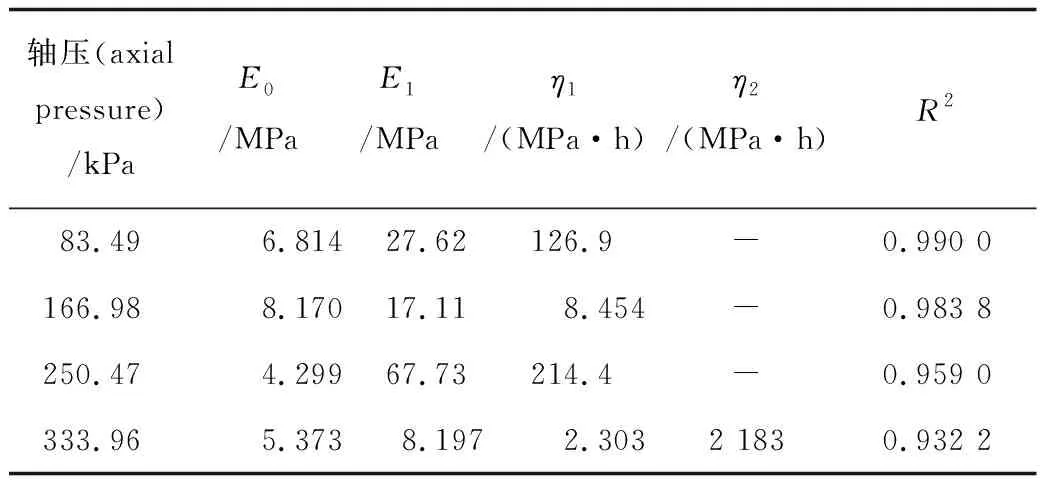
表3 经典西原模型拟合所得计算参数Table 3 Calculated parameters obtained from the fitting of the classical Nishihara model

表4 改进西原模型拟合所得计算参数Table 4 Improved calculation parameters obtained from Nishihara model fitting

图5 文献[12]蠕变试验的拟合曲线Fig.5 Fitting curves of creep tests in Reference [12]

软土在轴向应力为83.49，166.98 kPa下，如图5(a)～5(b)所示，经典西原模型和改进的西原模型拟合精度都比较高，决定系数都达到0.98以上，其中改进西原模型的拟合精度相比较经典西原模型的拟合精度更高一些，决定系数达到0.99以上。在轴向应力为250.47 kPa下，如图5(c)所示，软土相比较前2个应力水平下的蠕变速率有所增加，经典西原模型的决定系数为0.959 0，改进的西原模型的决定系数为0.982 5，可以看出，改进的西原模型在蠕变速率相对较大的情况下拟合效果更好。在轴向应力为333.96 kPa下，如图5(d)所示，软土出现了加速变形阶段，经典西原模型的决定系数为0.932 2，改进的西原模型的决定系数为0.991 1，改进的西原模型能够较好地反映软土在高应力条件下的瞬时变形、稳态蠕变和加速蠕变过程，整体拟合精度较高。

3 改进西原蠕变模型有限元实现及算例

本文利用ABAQUS软件提供的材料自定义本构开发接口UMAT，对改进西原模型进行二次开发。

针对南沙软土一维蠕变试验结果[13]运用MATLAB软件的最小二乘法进行参数拟合，参数拟合结果及精度如表5所示。由表5可知，得出的模型参数E0变化范围不大，其余参数变化规律明显。如图6 所示，其中E0的变化范围在870～930 kPa之间，E1，η1，c随着轴压的增加而成指数增大，而b随着轴压的增大而减小。

表5 改进西原模型拟合文献[13]所得计算参数Table 5 Improve the calculation parameters of Nishihara model fitting literature [13]

图6 蠕变参数与应力的关系Fig.6 The relationship between creep parameters and stress

为了验证所建模型及二次开发过程的可行性和合理性，建立与文献[14]室内试验规格相同的内径为6.18 cm，高度为8 cm的南沙软土圆柱体数值模型，荷载选用与原文室内试验相同的荷载，模拟试验共为6组，轴向应力分别为25，50，100，200，300，400 kPa。

在数值模拟过程中设置边界条件时，对模型底部进行完全固定约束，圆柱面进行U1和U2方向的位移约束。模型材料参数选定时，应利用多级应力水平下试验结果求出各模型参数的数学期望，并采用一些统计方法和优化方法，将会得到模型参数更为优化的值[15]。E0采用拟合值的平均值，其余参数根据表6中改进西原模型参数与应力关系选定。在上述步骤均按顺序完成后，在提交作业时，选中编辑好的用户子程序文件，得到的结果与试验结果作比较，如图7所示。可以看出在轴向应力为25，50，100，200，300，400 kPa下，ABAQUS中应用改进西原蠕变模型UMAT子程序的模拟试验结果与室内试验结果吻合良好，证明该程序能够很好地反映一维下软土瞬时弹性变形和衰减蠕变变形。需要指出的是，本文未研究三维状态下的改进西原模型参数与应力之间的关系及比较软土在三维应力状态下室内试验结果与模拟试验结果，这将是进一步要研究的内容。

表6 数值模拟参数Table 6 Numerical simulation parameters

图7 数值模拟结果与蠕变试验结果对比曲线Fig.7 Comparison curve between numerical simulation results and creep test results

4 结论

1)分析3种常用的经验蠕变模型对软土蠕变研究的适用性，对比分析发现幂函数在软土处于低应力状态下产生的瞬时弹性变形和衰减蠕变变形以及处于高应力状态下产生的加速蠕变变形都有着良好的拟合度，提出幂函数非线性元件。

2)改进后的西原模型能够较好地描述软土的非线性蠕变特性及软土在高应力水平下的加速蠕变变形阶段。

3)利用南沙软土的单轴试验结果与利用二次开发子程序模型模拟结果进行对比验证，结果表明有限元计算模型可以反映不同轴压下的蠕变关系，研究结果可进一步应用于相关岩土工程蠕变数值分析，为岩土工程蠕变分析多样化提供1种可行的方案。