大前石岭岩堆斜坡坡面爆破振动动力响应特征*

朱大鹏，谢昌建，阿布拉铁，许红波,3

(1.西南石油大学 地球科学与技术学院，四川 成都 610500；2.三峡库区地质灾害教育部重点实验室(三峡大学)，湖北 宜昌 443002；3.岳池县发展和改革局，四川 广安 638300)

0 引言

近年来，国内、外山区地质灾害多发，造成经济、人员重大损失，如崩塌、滑坡、泥石流等[1-2]。自然形成的岩堆往往松散堆积于山坡坡脚或平缓山坡处，直接威胁沿途铁路、公路等工程建设运营安全，对沿线工程建设构成巨大威胁，属于不良地质灾害之一。当隧道穿越岩堆斜坡至下伏坚硬基岩时，一般采用“洞口段附近及上覆岩堆注浆固结—基岩层钻爆掘进”方法[3]施工，以便同时确保坚硬基岩施工工期以及岩堆体安全。但过量的爆破用药会造成岩堆块体剧烈振动、翻滚、垮塌，甚至堵塞洞口。大前石岭隧道进口需穿越岩堆斜坡段，但目前类似的动荷载(隧道爆破施工振动、列车振动、地震等)对岩堆边坡稳定性影响的研究较少，振动响应机制不清，应力波传播规律不明，无可借鉴的较为成熟的评价方法。

由于岩堆坡面为自由面，不具有限制坡面岩块运动的约束条件，岩块更具有向下运动的趋势，危害更大。同时，爆破测振仪必须固定在岩块上保持与岩块同步振动，现有条件下难以对坡内速度进行监测。因此，振动强烈程度评价以坡面岩块速度为主，同时借助数值模拟展开进一步分析。

爆破振动下边坡振动速度越大，其振动效应越强烈，边坡稳定性越差。因此，常将质点峰值振动速度作为爆破振动动力响应安全判据。质点峰值振动速度衰减预测常采用前苏联科学院M.A.Садовский(萨道夫斯基)[4]根据实验归纳出的爆破作用下地面振动速度经验公式。针对隧道爆破掘进引起坡面振动速度预测，需要同时考虑坡面高程效应的影响[5]。

本构关系的表征是数值模拟手段必须克服的问题。由于岩堆块体为非连续体，颗粒流程序可以更好地描述颗粒离散关系。由于颗粒尺寸相近、形状相似，线弹性、小变形条件下有限元法同样可以近似地分析由于开挖、爆破引起的结构位移及变形。远离震源的坡面位置，岩堆块体的运动较为微弱，振动主要受应力波驱动，可将其力学行为仍视为处于弹性阶段；而直接遭受爆轰压力的粉碎区，块体开裂、粉碎，能量转换复杂，变形、破坏剧烈，塑性变形大，有限元的局限性则展露无遗。因此，有限元法可以有条件地模拟爆破作用下岩堆力学行为。Resende等[6]基于实测数据和有限元模型研究了地下洞室爆破作用斜坡振动及地震波传播规律，证实了有限元法的适用性；许红波[7]对大前石岭岩堆隧道围岩动力响应机制进行了研究；陈江[8]对高边坡洞口爆破响应规律进行了研究。除有限元(FEM)以外，快速拉格朗日法(FLAC)[9-11]、离散元法(DEM)[12]同样可以进行岩堆受动力作用下的响应机制研究。但受块体连续性、均匀性影响，特别是不同岩块之间的挤压、碰撞，其应力状态并不与FEM，FLAC所构建的连续性一致，而是容易造成块体内部、块体与块体之间应力集中，从而影响整体的应力分布状态，这也是现在二者无法克服的困难之一。

目前少见对爆破作用下呈破碎状的松散岩堆体坡面响应规律及爆破参数影响的研究。因此，为获得振动对岩堆边坡影响的认识，在对隧道开挖、爆破过程开展现场振动监测的基础上，构建岩堆斜坡爆破振动三维有限元模型，根据现场实测爆破振动速度峰值进行数值模拟验证，探索爆破作用下岩堆斜坡坡面位移、速度以及加速度在不同方向、坡面位置以及用药量下的响应规律及机理，准确评价岩堆斜坡爆破振动速度、明确岩堆斜坡爆破振动特征和机理是隧道爆破掘进维持斜坡稳定性和经济、安全施工的基础，可为指导现场安全爆破施工提供重要参考。

1 工程概况

大前石岭深厚岩堆位于辽宁省田师傅-桓仁铁路东段与通惯线交汇处，坡度20°～38°，主要由石英砂岩岩块、碎石及粉质黏土、粉细砂等第四系崩积物(Q4col) 组成，岩块粒径0.3～1.2 m，棱角状。施工前对进口局部范围内松散岩堆体注浆加固形成较高强度胶结体以确保洞壁具有较好的自稳性。由于厚层石英砂岩基岩质地坚硬，采用2号岩石硝铵炸药以及不耦合装药系数约1.4～2.0的装药结构爆破，非电毫秒雷管起爆。除炸药量改变外，炸药种类、装药结构以及炮孔布置等基本不变，每次起爆可视为仅药量的变化。

2 岩堆斜坡爆破振动数值模拟

尽管通过现场岩堆斜坡爆破振动速度监测判定爆破过程中处于安全状态，但由于监测数量以及现场条件限制，非监测点是否处于安全状态有待进一步确定。因此，有必要通过更全面、更有效的数值模拟方法来确定岩堆斜坡不同部位的位移、速度、加速度响应规律，为岩堆斜坡爆破振动安全评价以及现场爆破用药预测提供重要参考。

2.1 模型建立

依据大前石岭岩堆隧道进口段岩堆层、崩坡积层、基岩层简化建立有限元模型如图1所示。沿斜坡坡面方向从洞口位置每隔12 m布置1个监测点，共布置5个监测点，编号依次为边-1～边-5，重点分析隧道进尺50 m、药量20 kg时斜坡坡面动力响应规律。测点边-3位于爆破掌子面正上方。根据土工试验确定材料参数见表1。

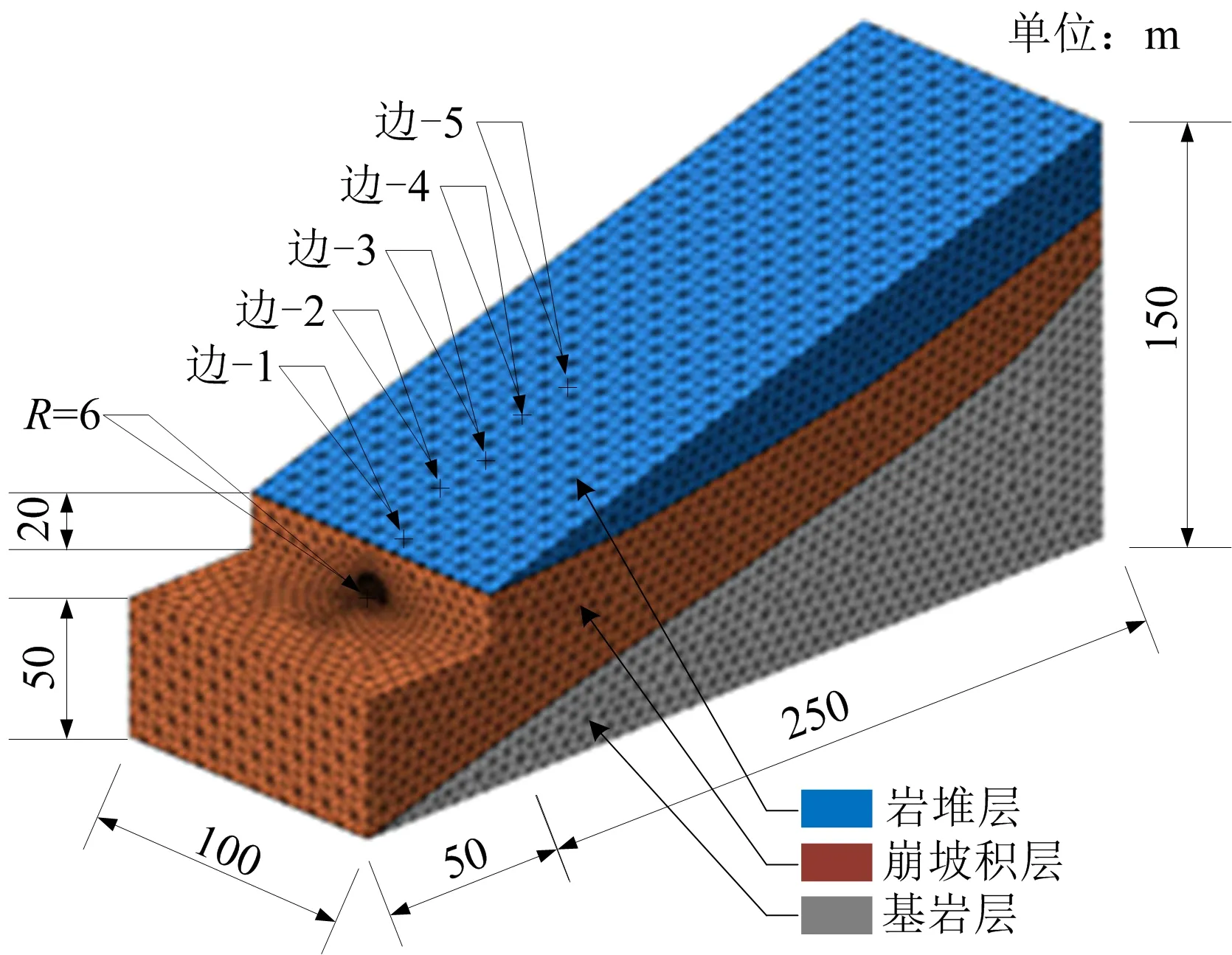
图1 有限元模型及监测点Fig.1 Finite element model and monitoring points

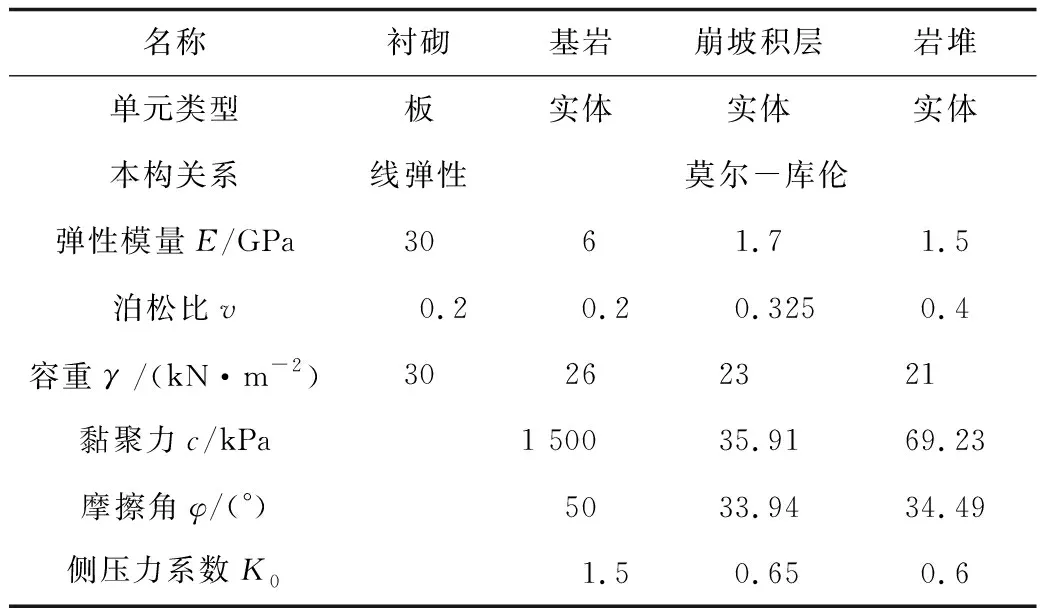
表1 岩土层及衬砌材料属性Table 1 Material properties of rock soil and lining

2.2 震动分析

采用黏性边界条件以消除人工边界对地震波的影响。P波、S波黏性系数分别为4.16×105,2.54×105Pa·s，边界弹簧系数kx，ky，kz分别为58 613，69 636，53 697 kN/m，Raylcigh阻尼比为0.05。振型1周期为0.956 910 s、振型2周期为0.572 170 s。爆破荷载模型采用三角形荷载，采用HY Low式计算峰值荷载。三角形爆破荷载作用曲线如图2所示。

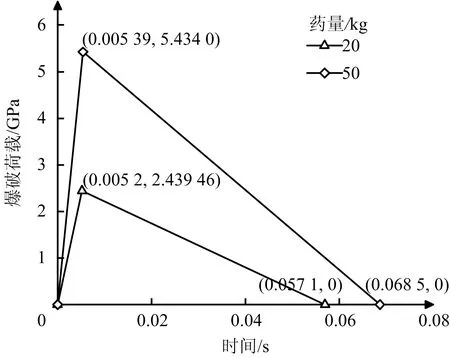
图2 三角形爆破荷载作用曲线Fig.2 Triangular blasting load curve

3 爆破速度反演及数值模拟验证

3.1 爆破振动速度反演

同一掌子面一般仅爆破1次，药量根据实际情况选取，爆心距、高差等也会随掌子面位置的不同而改变。在多参数影响下，不便于对数值模拟结果进行对比验证。一般将质点最大振动速度作为评判斜坡是否处于安全状态的依据。运用考虑高程因素对衰减规律影响的朱传统公式[5]进行速度反演，其在岩堆斜坡爆破振动速度方面拟合较好[7]，如式(1)所示：

(1)

式中：V为质点峰值速度，cm/s；K为爆破场地系数；Q为爆破药量，kg；R为爆心距，即斜坡坡面质点距离爆破中心的距离，m；H为坡面相对高程，m；α为地质条件系数；β表示高程影响系数，β>0表示衰减，β<0表示放大。

现有《爆破安全规程》(GB 6722—2014)[13]并未给出岩堆爆破振动K,α参考值，通过现场监测数据拟合得到各参数及相关指数R2，见表2。

表2 朱传统公式各方向速度拟合参数Table 2 Fitting parameters of velocity in each direction of formula by ZHU Chuantong

因岩堆斜坡结构松散，离散性大，受样本差异影响，导致整体拟合度均不达0.9，但整体拟合效果较好。同时，上述规范推荐坚硬岩石的K值为50～150,α值为1.3～1.5。由表2可知，该岩堆斜坡各方向K,α值差异较大，反映了岩堆结构的各向异性。根据数值模拟条件，将表2参数代入式(1)，即可得到与实测值近似的反演值。另外，相比整体性好的完整岩体[14]，其K，α值明显降低，与岩堆结构孔隙和结构面众多有关[15]。大前石岭岩堆垂直方向速度K，α推荐值分别在30，1.2左右。

3.2 数值模拟验证

为确保所建立的数值模型与实际相符，将各方向振动速度作为验证依据。模型所用药量为50 kg、隧道进尺50 m，对比岩堆隧道进口段底面中部距爆破掌子面20～70 m每隔10 m处的各方向峰值速度模拟值与现场实测数据反演值，如图3所示。隧道轴线方向指向洞门为X轴正方向，垂直纸面向外为Y轴正方向，垂直向上方向为Z轴正方向。

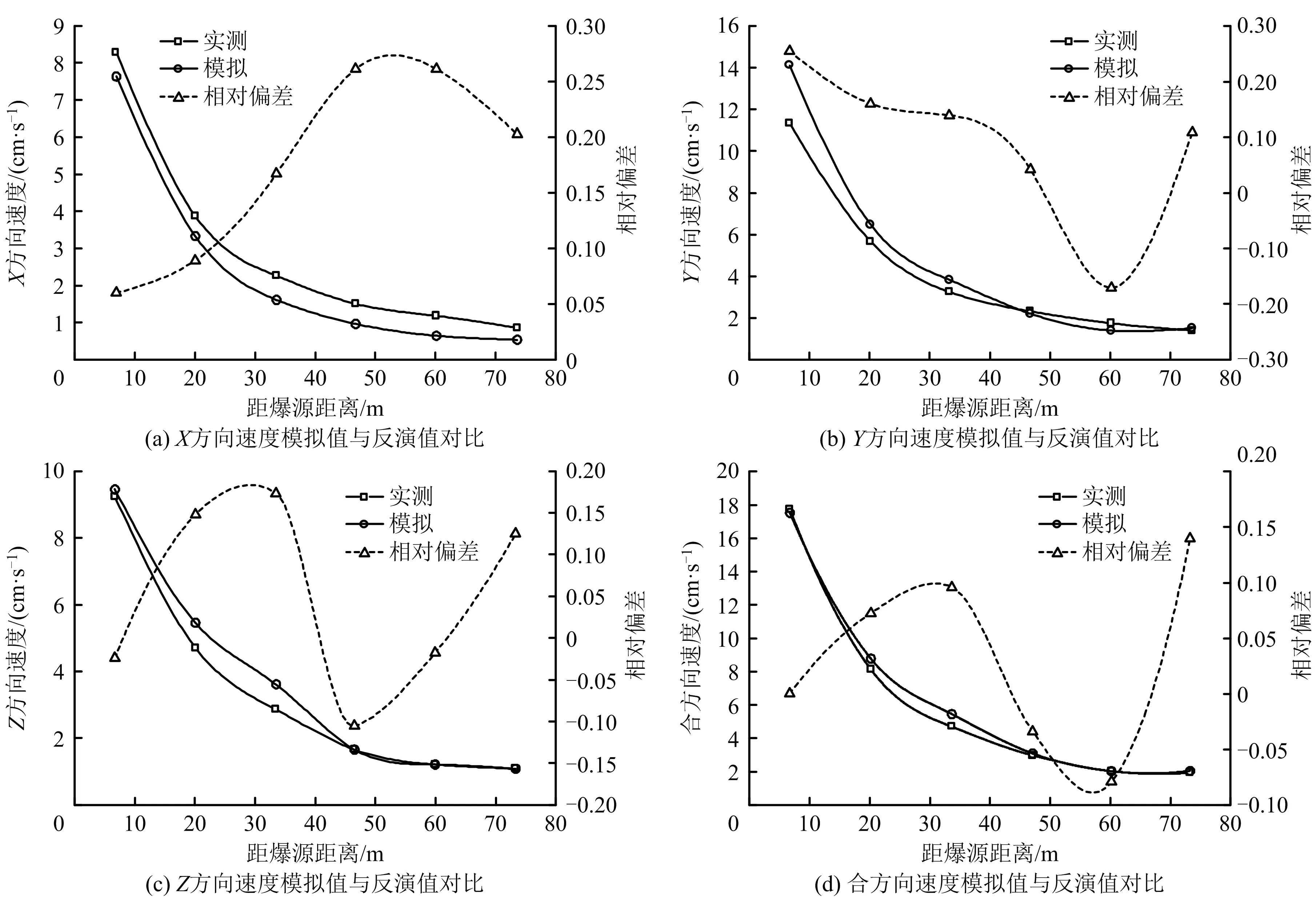
图3 各方向速度模拟值与反演值对比Fig.3 Comparison on velocity of simulation and inversion in each direction

由图3可知，模拟值相比根据实测数据得到的反演值，各方向速度衰减整体变化趋势基本一致，X，Y，Z方向速度以及合方向速度平均相对偏差分别为17.3%，9.6%，14.7%，6.9%，即除VX相差较大以外，其余速度拟合度较高。总体速度衰减趋势一致且整体相差不大，都为“先快后慢”式衰减。因此，有限元法能较准确地模拟岩堆爆破振动动力响应情况，可作为后续动力响应分析基础。

4 洞口岩堆斜坡坡面爆破振动响应规律

目前对爆破作用下呈破碎状的松散岩堆体坡面响应规律及爆破参数影响的研究较少，因此，选取坡面振动主要特征进行分析。坡面振动主要特征包括峰值位移、峰值速度以及峰值加速度。不同振动方向、不同坡面位置以及不同药量下振动强度不同。爆破强弱主要受药量影响，因此，重点分析药量一定(20 kg)、爆破位置相同(进尺50 m)情况下不同方向位移、速度和加速度响应规律以及与振动方向、坡面位置以及药量的关系。

各测点相对爆源的距离为：边-3<边-2<边-4<边-1<边-5。Q为爆破药量，kg；SX，SY，SZ分别为X，Y，Z方向位移，mm。VX，VY，VZ分别为X，Y，Z方向速度，cm/s；aX，aY，aZ分别为X，Y，Z方向加速度，m/s2。

因此，为获得振动对岩堆边坡影响的认识，在对隧道开挖、爆破过程开展现场振动监测的基础上，构建岩堆斜坡爆破振动三维有限元模型，根据现场实测爆破振动速度峰值进行数值模拟验证；探索爆破作用下岩堆斜坡坡面位移、速度以及加速度在不同方向、坡面位置以及用药量下的响应规律及机理。

4.1 位移响应规律

边-3测点的X，Y，Z方向位移响应曲线如图4所示。由图4可知，各方向最大位移分别为0.1，0.1，1.3 mm。SX，SY相差不大、但相对Z方向小很多，SZ约为SX，SY最大位移的13倍。故当爆破进尺、炸药量一定时，掌子面上方垂向为主要变形方向，其余方向变形较小。

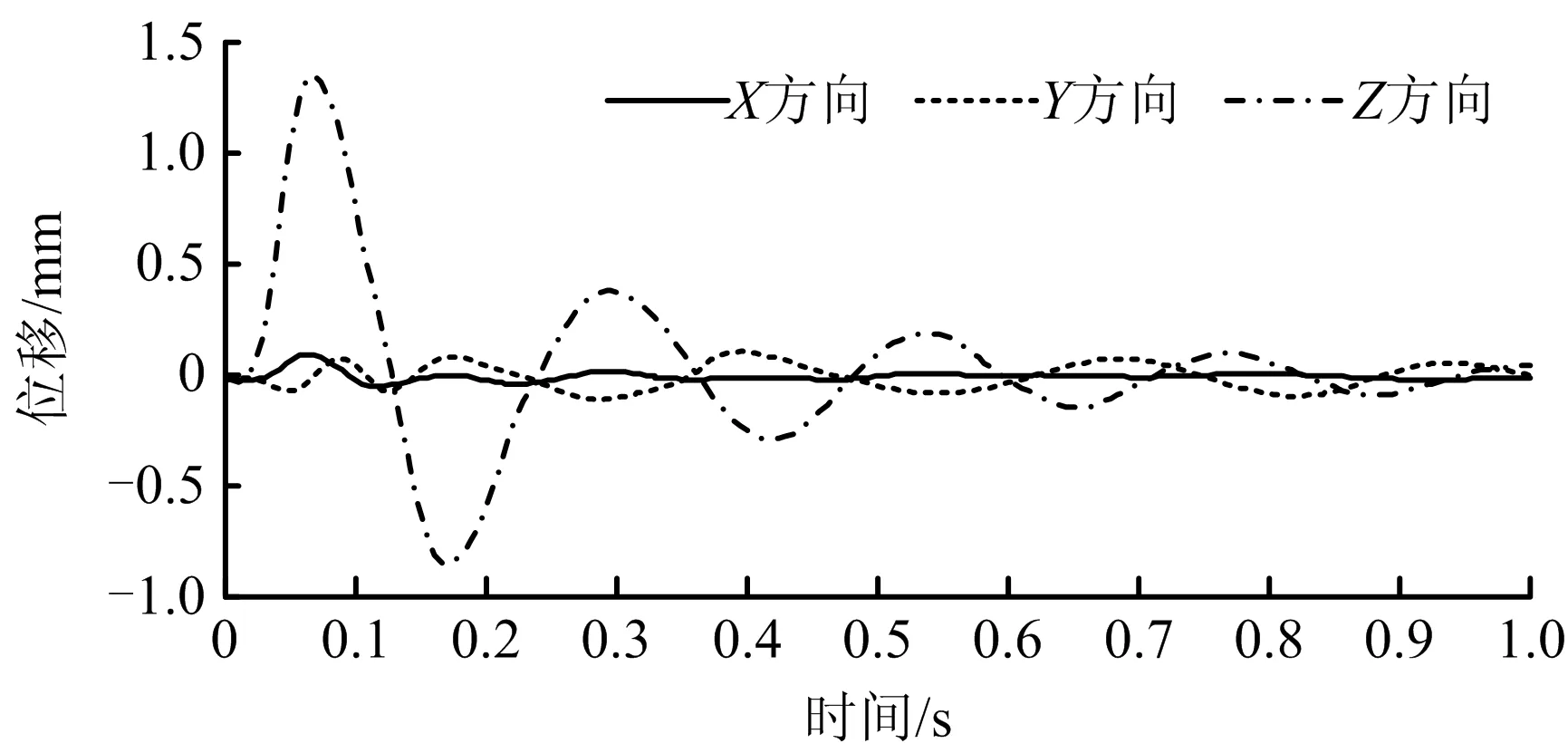
图4 边-3测点不同方向上的位移Fig.4 Displacement in different directions of slope-3 measuring point

各测点Z方向位移响应曲线如图5所示。由图5可知，位移相对大小为：边-3>边-2>边-4>边-1>边-5。一般离爆源越近，波的传播距离越小，衰减越弱，振动越强烈，与实际情况基本一致。

图5 坡面不同位置的Z方向位移Fig.5 Displacement in Z-direction at different positions on slope surface

边-3测点在药量为5，15，30，50 kg条件下掌子面上方岩堆斜坡产生的最大垂直位移分别为0.3，1.0，2.0，3.4 mm，如图6所示。药量与最大垂直位移线性拟合可得：SZmax= 0.068 7Q-0.042 4(R2=0.999 9)。因此，药量不同时岩堆斜坡处产生的最大垂直位移与药量具有较强的线性关系。

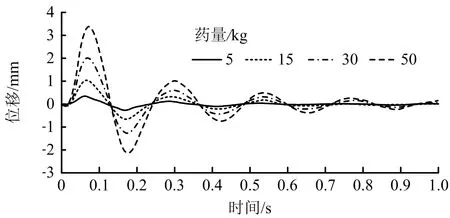
图6 边-3测点不同药量下的Z方向位移Fig.6 Displacement in Z-direction of slope-3 measuring point under different quantities of explosives

4.2 速度响应规律

边-3测点的X，Y，Z方向速度响应曲线如图7所示。由图7可知，各方向最大振动速度分别为0.4，0.5，4.6 cm/s。VZ相比VX，VY大约10倍，VX，VY相差不大。故当爆破进尺、爆破用药一定时，掌子面上方垂向振动速度比横向、纵向振动更强烈，为爆破荷载下坡面的主要运动方向。

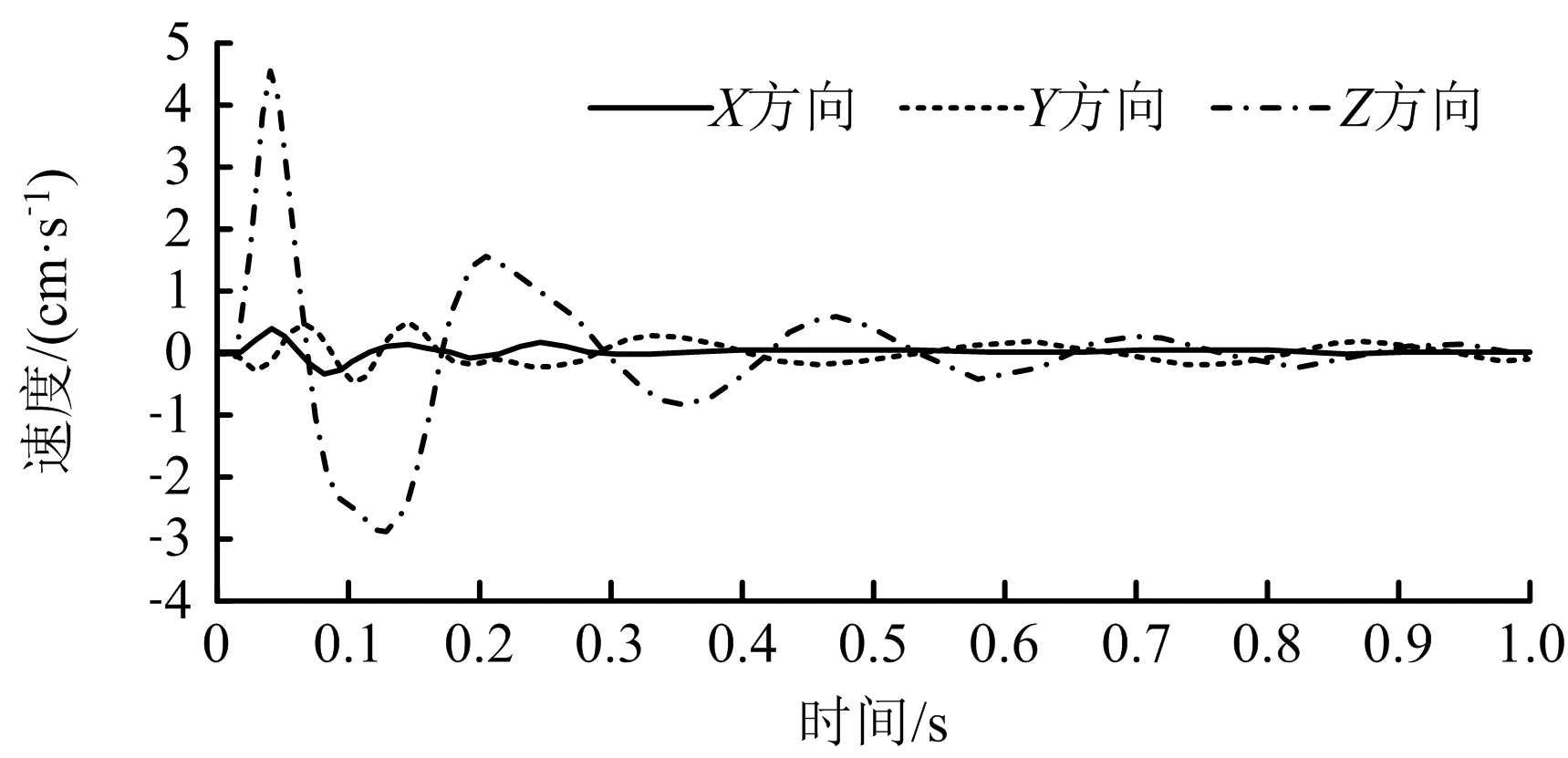
图7 边-3测点不同方向上的速度Fig.7 Velocities in different directions of slope-3 measuring point

各测点Z方向振动速度响应曲线如图8所示。由图8可知，峰值速度相对大小为：边-3>边-2>边-4>边-1>边-5。距离爆源越近，岩堆斜坡的峰值振速越大。

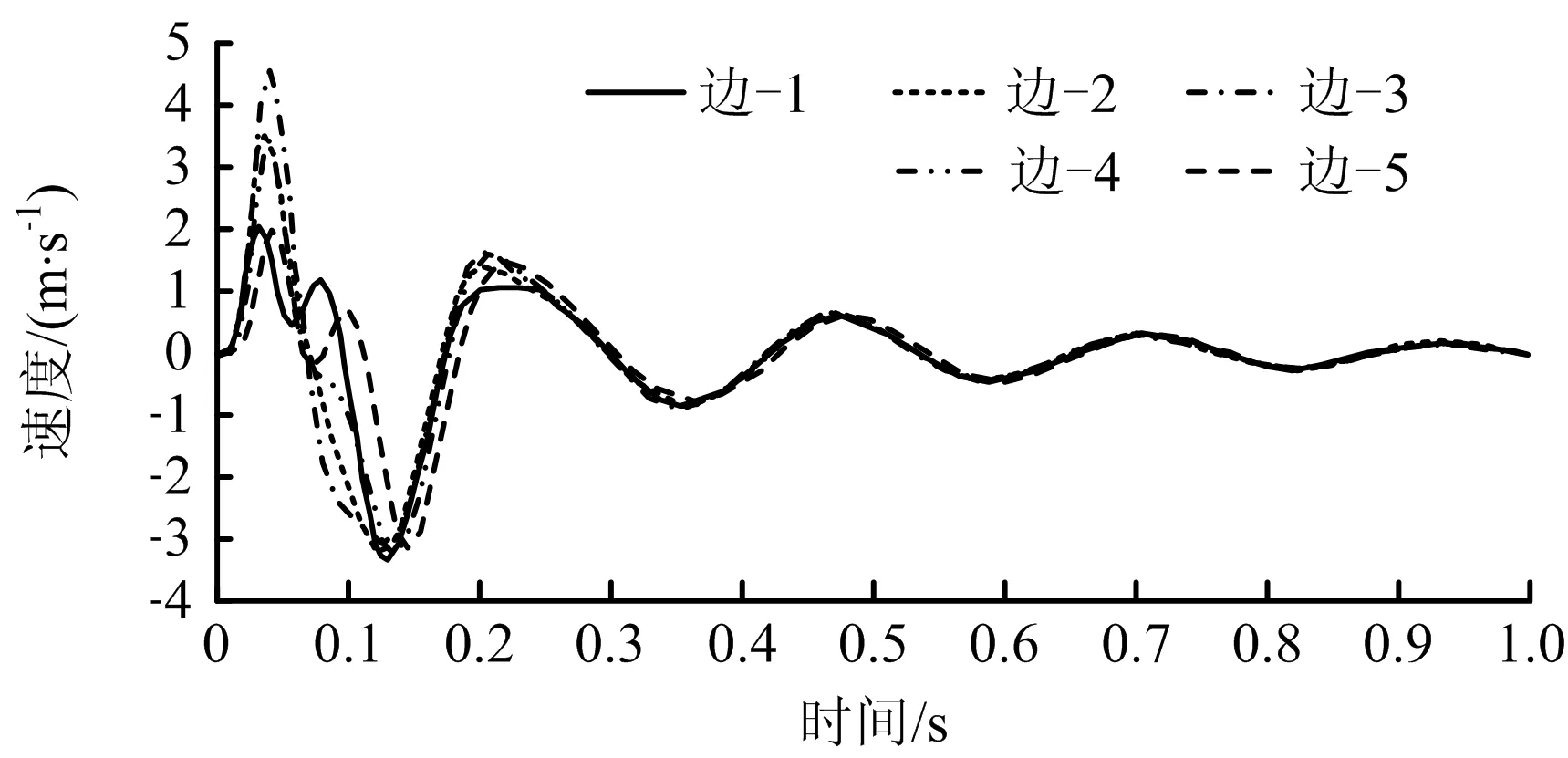
图8 坡面不同位置的Z方向速度Fig.8 Velocities in Z-direction at different positions on slope surface

边-3测点在药量为5，15，30，50 kg条件下VZ响应曲线如图9所示。由图9可知，Z方向峰值振速分别为1.3，3.5，6.6，10.6 cm/s。Q与峰值VZmax线性拟合可得：VZmax=0.206 1Q+0.347 8(R2=0.999 6)。因此，药量不同时岩堆斜坡处产生的峰值速度与药量具有较强的线性关系。

图9 边-3测点不同药量下的Z方向速度Fig.9 Velocities in Z-direction of slope-3 measuring point under different quantities of explosives

4.3 加速度响应规律

边-3测点的各方向振动加速度响应曲线如图10所示。由图10可知，X，Y，Z方向峰值加速度分别为0.3，0.4，2.4 m/s2，aZ约为aX的8倍、约为aY的6倍，aX，aY相差不大。即当爆破进尺、用药量一定时，掌子面上方垂直方向产生较水平方向更大的振动趋势，为爆破荷载下坡面的主要运动方向。

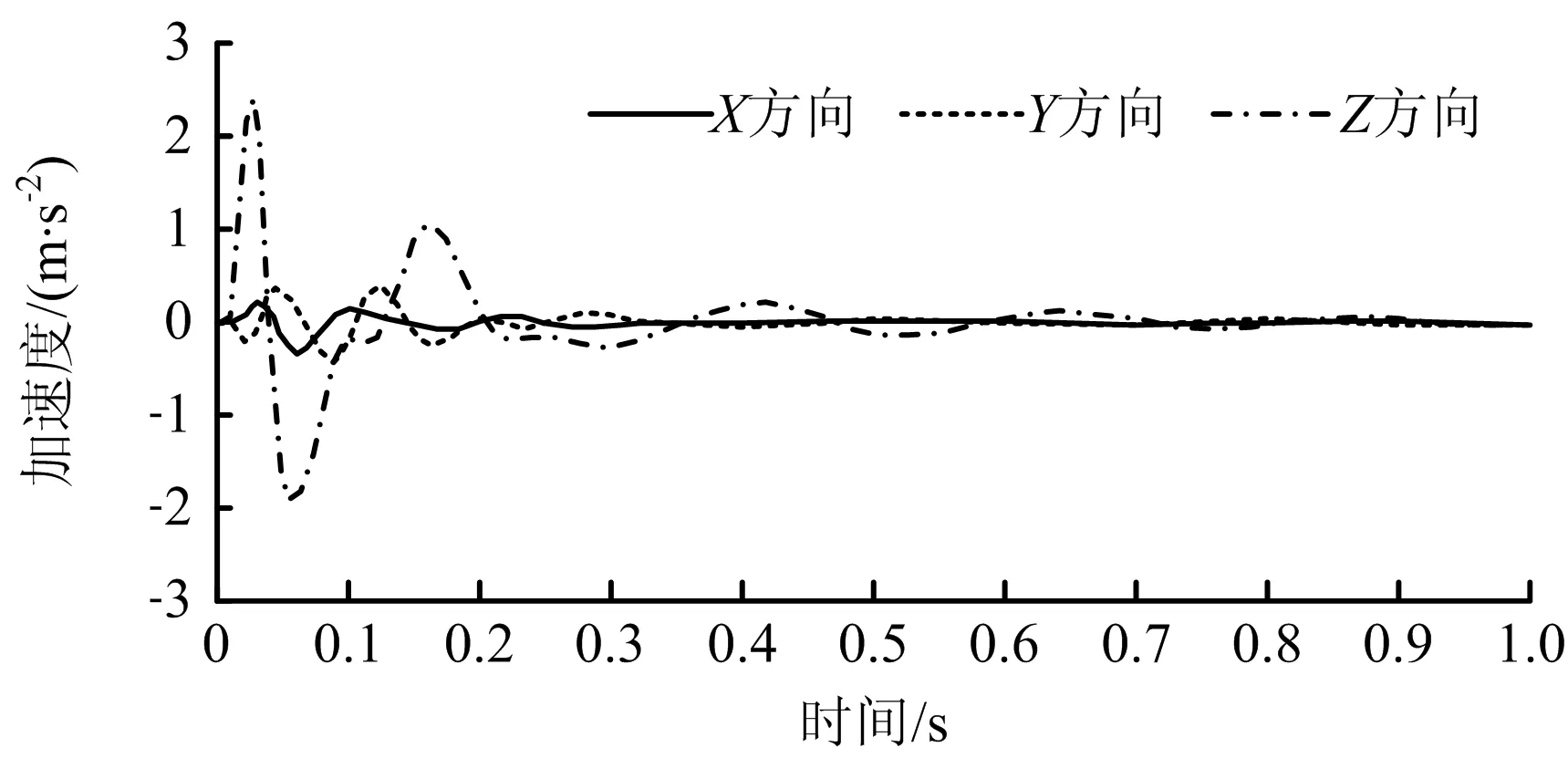
图10 边-3测点不同方向上的加速度Fig.10 Acceleration in different directions of slope-3 measuring point

各测点Z方向振动加速度响应曲线如图11所示。由图11可知，振动加速度相对大小为：边-3>边-2>边-1>边-5>边-4。由于数值模拟中坡面形态与实际地形地貌等之间存在一定差异，因此，除边-4点以外，其基本与实际一致。因此，距离爆源越近，岩堆斜坡的峰值加速度越大。

图11 坡面不同位置的Z方向加速度Fig.11 Acceleration in Z-direction at different positions on slope surface

边-3测点在药量5，15，30，50 kg条件下aZ响应曲线如图12所示。由图12可知，峰值aZmax分别为0.7，1.9，3.5，5.6 m/s2。药量Q与aZmax线性拟合可得：aZmax=0.108 3Q+0.218 5(R2=0.999 3)因此，药量不同时岩堆斜坡处产生的峰值加速度与药量具有较强的线性关系，即药量越大、峰值加速度越大，且基本呈线性增大关系。

图12 边-3测点不同药量下的Z方向加速度Fig.12 Acceleration in Z-direction of slope-3 measuring point under different quantities of explosives

线弹性、小变形假设下，药量与位移峰值、速度峰值、加速度峰值之间均具有线性关系，说明基于有限元法的岩堆爆破振动分析是可行的。

5 结论

1)爆破振动引起的岩堆体位移、速度及加速度在爆破后迅速达到峰值，随时间推移呈波浪状“先快后慢”式衰减。

2)岩堆坡面垂直振动最剧烈，水平方向和隧道轴线方向整体相差不大。垂直方向相比其余2个方向位移、速度和加速度大几倍到十多倍不等。

3)坡面位移峰值、速度峰值、加速度峰值与爆破掌子面距坡面距离基本呈负相关关系，与爆破药量基本呈线性增加关系。

4)离爆破掌子面最近的岩堆斜坡坡面处垂直方向峰值振速为最大振动速度，该点为现场爆破振动安全评价关键点。

5)考虑高程影响的朱传统公式在岩堆斜坡爆破振动速度预测方面具有较好的适用性，垂直方向速度的K，α值推荐值分别在30，1.2左右。该公式可用于相关安全评价及速度预测。