高速铁路箱梁−无砟轨道结构温度场模型的级数解
戴公连,张强强,刘文硕,黄志斌
(1.中南大学土木工程学院,湖南长沙,410083;2.东南沿海铁路福建有限责任公司,福建福州,350013)
桥上无砟轨道是我国高速铁路主要的轨道结构形式,桥梁体系的箱梁轨道系统的温度作用模式是高速铁路桥梁轨道结构设计中必须考虑的因素之一。对于桥上轨道结构而言,中国高速铁路规范[1]规定无砟轨道结构的竖向正温度梯度为90 ℃/m,通过对无砟轨道温度梯度的实测及分析发现[2−3],我国中部地区的无砟轨道温度梯度普遍高于80 ℃/m,实测温度梯度甚至达到100 ℃/m。由于轨道结构的遮挡效应,桥梁顶面的温度场呈现不均匀性,对处于施工或服役状态的桥梁温度分布及温度效应的影响也均不同[4−5]。现有的中国规范、欧洲规范均没有给出相应的箱梁−无砟轨道结构的温度计算模式,因此,箱梁轨道系统的温度分布特征仍亟待进一步研究。目前,很多学者主要采用数值模拟、统计分析等方法对轨道板和箱梁的温度梯度分布模式与温度取值进行了大量研究。闫斌等[6]利用无砟轨道温度场的有限元模型,分析了地理位置、热物性参数、环境等因素对无砟轨道温度梯度的影响。朱劲松等[7]建立了桥−轨温度场精细化有限元模型,研究了遮挡效应对结构温度场的影响。戴公连等[8]利用CRTS Ⅱ型轨道板的实测结果建立了箱梁−无砟轨道结构的温差GPD 极值模型,给出了具有一定概率的轨道结构温度取值。申建康等[9]应用机器学习的方法对轨道板温度场进行预测,具有很高的预测精度。但在实际工程中,研究者大多采用半理论半经验公式或全经验公式预测桥梁结构的温度。ABID等[10]利用逐步回归法拟合得到由环境参数(太阳辐射量、大气温度及风速)预测试验梁温差的经验公式,拟合度R2=0.97。刘学毅等[2]给出了一种快速计算高速铁路道床板温度的公式,简化了实际中道床板温度的预测方法,但没有涉及箱梁温度场的计算,无法形成一个整体的箱梁−无砟轨道结构温度预测方法。在既有的高速铁路桥梁温度场研究中,解析法具有较高精度[11],易于分析环境变量对结构温度的影响。为此,本文作者结合实测温度建立第三类边界的箱梁−无砟轨道板温度场的数学模型,采用积分变换法推导结构导热微分方程的级数解,并与结构的实测结果和数值结果进行对比验证。同时,参考相关规范提出箱梁−无砟轨道结构温度场的四折线及指数分布曲线,并给出箱梁−无砟轨道结构升温模式的计算方法。
1 结构热交换分析
1.1 结构与环境的热交换
桥梁结构与外界环境的热交换可分为太阳辐射、对流换热及辐射换热,具体热交换方式如图1所示。
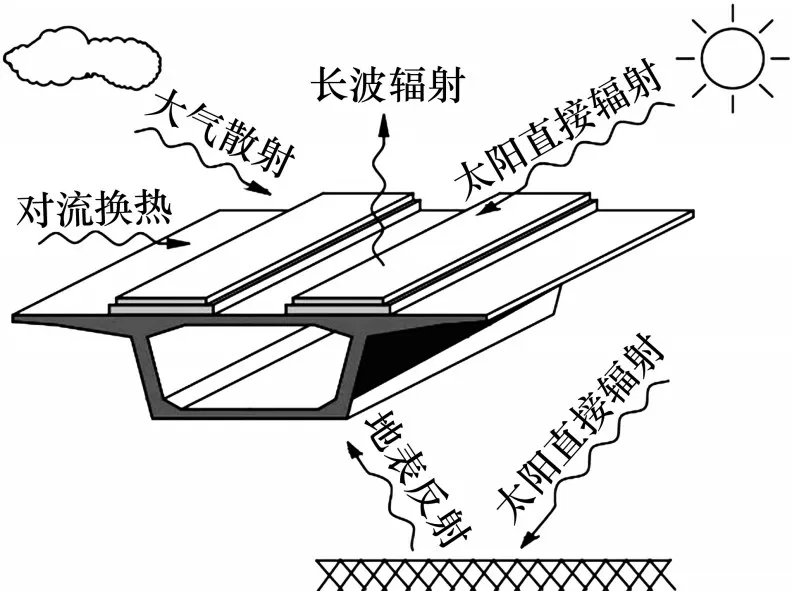
图1 箱梁-无砟轨道结构的热交换示意图Fig.1 Schematic diagram of heat exchange of box girder-ballastless track structure
以箱梁−轨道结构的水平面热交换为例,太阳辐射到结构表面上,以辐射平衡等式得到结构表面的第二类边界条件:
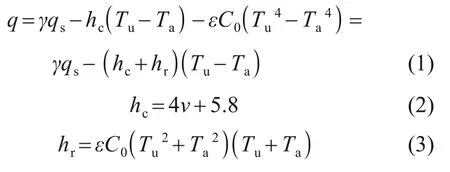
式中:γ为混凝土表面的太阳辐射吸收系数,本文取0.5[12];qs为太阳辐射强度,W/m2;v为风速,m/s;ε为混凝土表面的黑度系数,取0.88[12];C0为Stefan-Boltzmann常数,其值为5.67×10−8W/(m2∙K4);Tu和Ta分别为混凝土表面温度、大气温度(℃);hc为对流换热系数,W/(m2∙K),其取值与风速有关[12−13];hr为辐射换热系数,W/(m2∙K),可根据结构表面的辐射换热公式(式(3))计算。
令h=hc+hr,代入式(1)可得
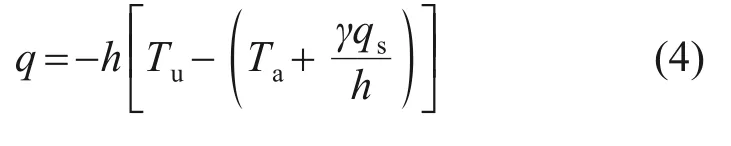
将大气和太阳辐射与结构的热交换作用看作等效辐射气温[13−14],用参数Te表示。

可得到结构表面的第三类边界条件:

另外,当无太阳辐射情形或结构处于遮阴面时,qs取0 W/m2,则Te=Ta。
1.2 结构热阻网络图
为更好地理解辐射气温的换热作用及物理含义,采用热阻网络图反映结构的综合对流换热过程,如图2所示。根据热阻的定义,可得到结构外表面的热阻Qin表达式(见式(7))。当结构表面的面积A取单元面积,热源Qst取0 W/m2时,式(7)与对流换热式(6)相一致。
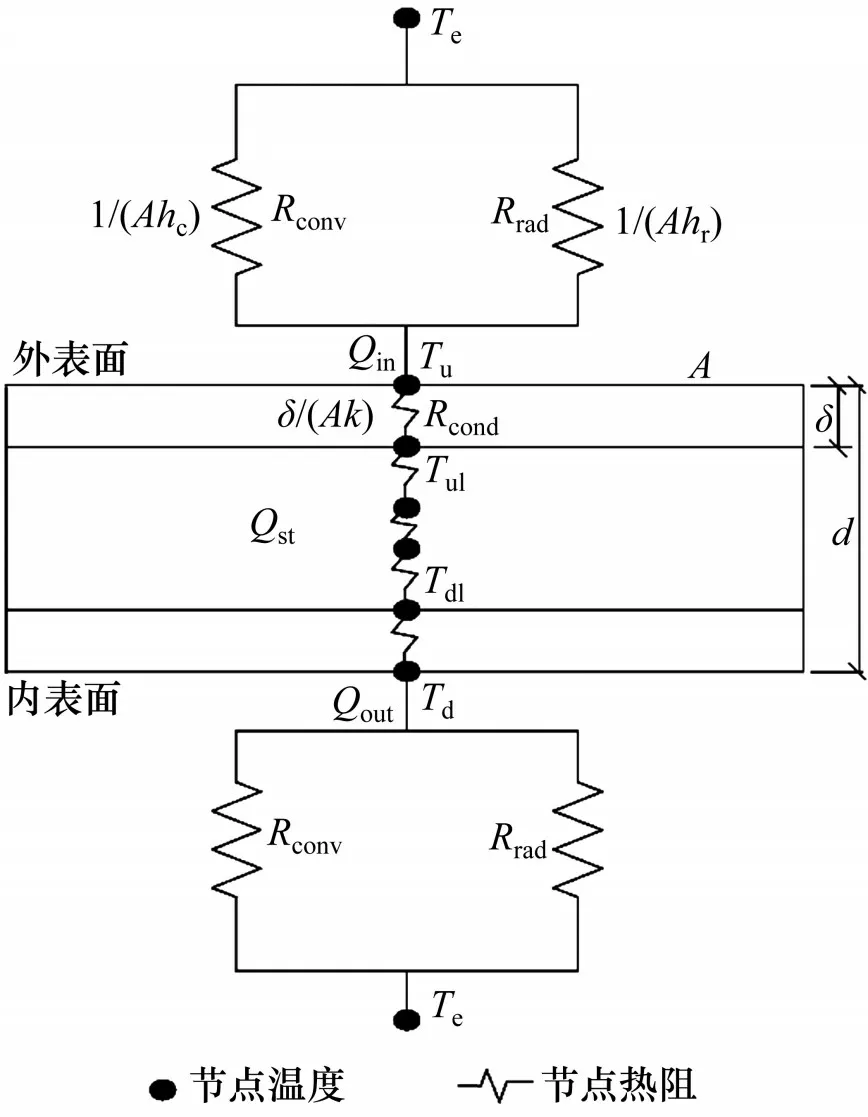
图2 结构热交换的热阻网络图Fig.2 Thermal resistance network of structural heat transfer

式中:Rconv和Rrad分别为结构表面的对流热阻和辐射热阻,K/W,可分别用1/(Ahc)和1/(Ahr)计算得到。
同理,结构内表面热交换量Qout为
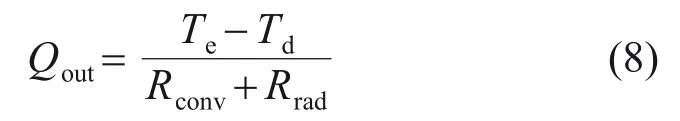
式中:Td为箱梁内表面的待求温度,℃。对箱梁−无砟轨道结构进行离散,单元热节点的导热量表达式为
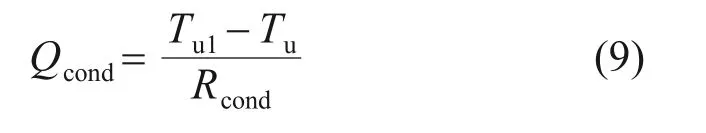
式中:Rcond为单元热节点Tu1和Tu的导热热阻,表达式为δ/(Ak),与相邻的热节点间的距离δ呈正比。
建立结构热节点的能量平衡方程组进行差分求解,求得结构体系各构件温度。
2 结构温度场模型及求解
根据热流边界条件转换方法,建立对流边界条件的结构热传导微分方程。首先,假定混凝土结构的热物性参数不随时间变化,将结构温度场简化为一维瞬态、无内热源的边值问题(BVP)。其次,确定流体温度的函数表达式。太阳辐射下结构表面的流体温度呈周期性变化,可用简谐波描述:
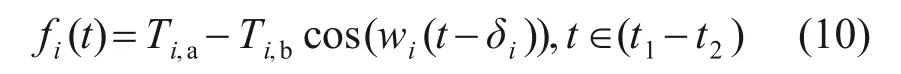
式中:i为结构边界的个数;Ti,a和Ti,b分别为第i个边界处太阳辐射时间内流体介质的平均温度和幅值;wi和δi分别为第i个边界处函数的频率及相位;t1和t2分别为日出和日落时间。
结构边界条件确定后,需要指定结构的初始条件。根据本文的实测结果及文献[15]的研究结果得到:夏季每天6:00 左右,结构温度场分布较均匀,因此,以t1时结构均匀温度为温度场模型的初始温度T0。
高速铁路桥梁结构为有限截面,则一维混凝土结构的导热微分方程为

式中:α为混凝土材料的热扩散系数;d为一维混凝土结构的截面高度。
为使结构温度场的初始扰动为零,引入温度变量θ(x,t):
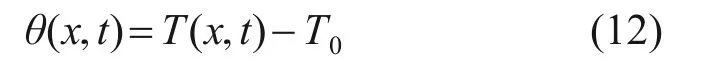
将式(10)代入导热方程(11),得到结构温度的控制方程为
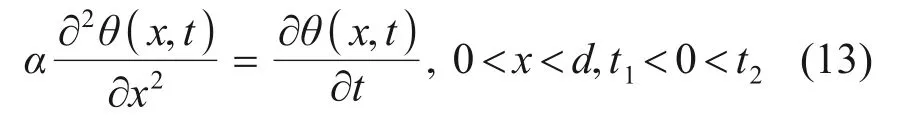
则结构上表面(x=0)的对流边界条件为

结构下表面(x=d)的对流边界条件为
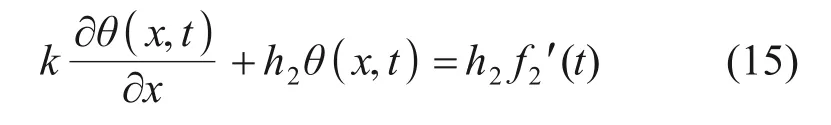
结构的初始条件为

式中:k为混凝土导热系数;h1和h2分别为结构外表面、内表面的综合对流换热系数;fi′(t)为结构表面流体温度式(式(10))的变形式。
为简化求解过程,对式(10)进行变换:
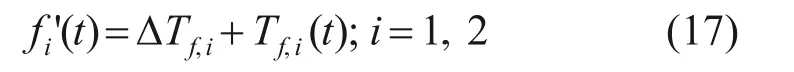
式中:ΔTf,i=Ti,a-T0;Tf,i(t)=-Ti,bcos(wi(t-δi))。
通过引用温度变量对原导热方程进行转换,得到的控制方程可采用积分变换法进行求解。由双对流边界条件式(14)和(15)可以确定本征函数式X(βn,x)和本征值βn的超越方程为[16]:
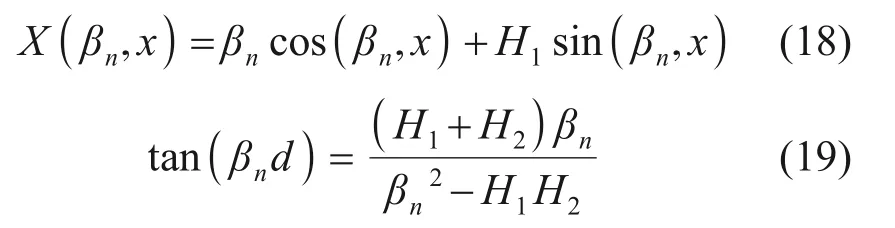
采用分离变量法对控制方程进行变量分离,可得到其解的正、逆函数变换式[16]:

式(20)为逆变公式,式(21)为积分变换式。
将式(21)代入逆变式(20),可得到控制方程的一般解[16]:
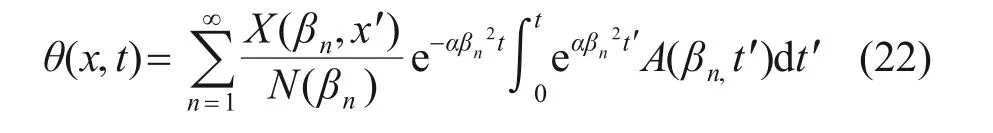
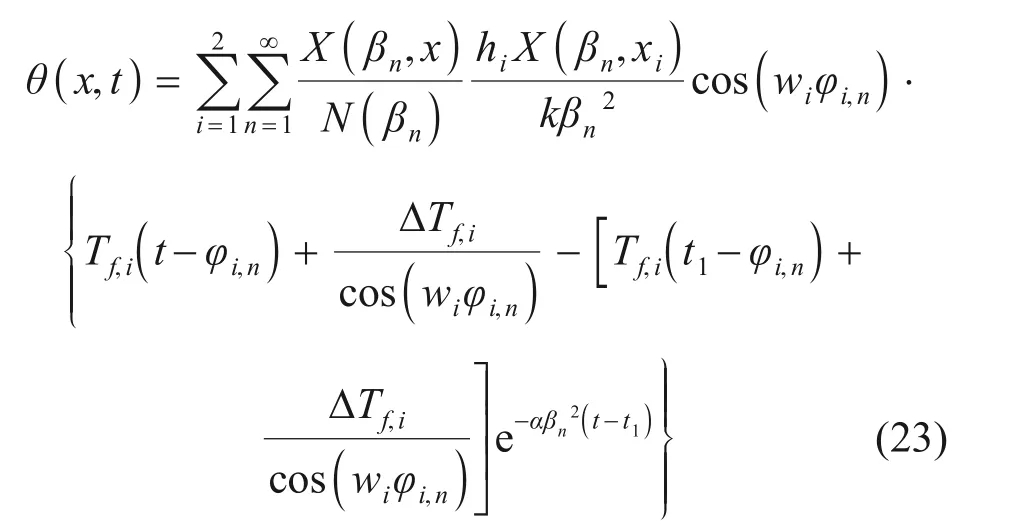
将式(12)代入式(23),可得原方程的级数解为
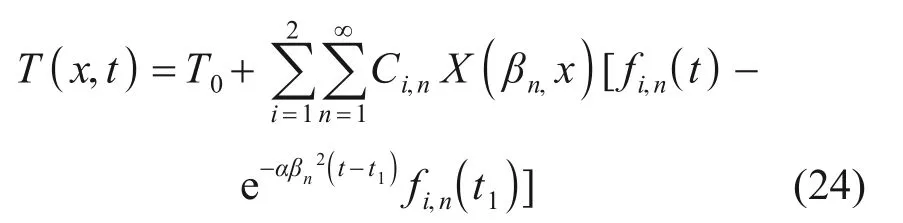
式(24)中,T(x,t)为一维混凝土温度场模型的叠加表达式,由于大体积或截面过高的结构初始温度分布不均匀,会产生一定的计算误差;当初始温度取值确定后,结构温度场的计算精度与级数展开项数n有关,一般项数越多,精度越高[16]。仅需要确定结构边界的流体温度表达式,即可计算箱梁−无砟轨道结构中任一构件的温度。
3 模型验证
在江西境内的1座32 m高速铁路箱梁−无砟轨道板中预埋多个温度传感器,并连续进行4 a 观测。采用预埋BGK-3700 温度计作为温度测量元件,利用分布式网络测量系统,每隔30 min 进行实时采集,温度测点布置如图3所示。
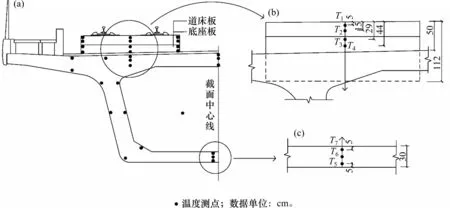
图3 结构截面的温度传感器分布Fig.3 Distribution of temperature sensors of structural section
3.1 定解条件
根据现场实测结果统计得到无砟轨道板的竖向温差在夏至日(7月23日)前后达到最大值,约17 ℃,因此,本文仅对夏至前后几天的实测温度进行理论建模及分析。利用2014−07−19 至2014−07−25 连续升温的实测温度建立箱梁−无砟轨道结构和箱梁底板的温度场模型。
为避免结构的初始温度对温度场计算产生误差,选取连续升温的第3天(2014−07−22)的实测温度确定温度场模型的边界条件及初始条件,如图4所示。2014−07−22,太阳辐射较有规律地发生变化,最大辐照度为800 W/m2左右。
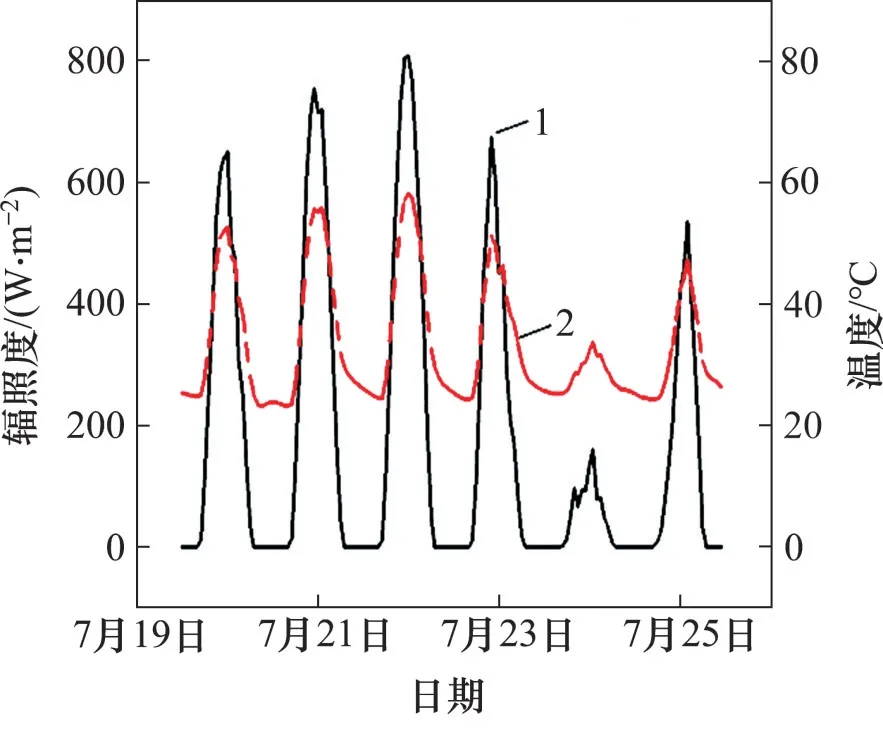
图4 2014年辐射气温和太阳辐照度的时程曲线Fig.4 Time history curves of radiation temperature and solar irradiance in 2014
太阳升起时刻为6:00,据此计算得到箱梁−轨道板和箱梁底板的均匀温度分别为34 ℃和25 ℃。忽略温度场分布的微小差异(偏差约2 ℃),令初始温度T0分别为34 ℃和25 ℃。
采用Fourier函数拟合日照时间(6:00—18:00)范围内轨道板表面的辐射气温,并转化为余弦形式:
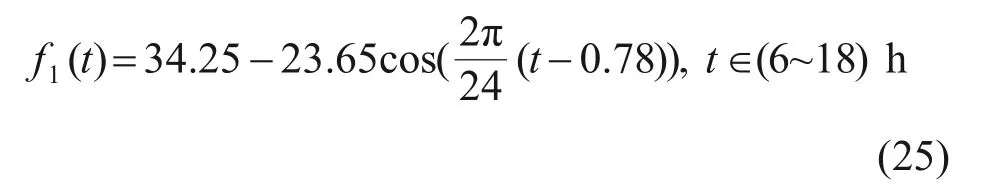
箱梁底板无太阳辐射,日气温变化可用以下经验公式[17]表示:
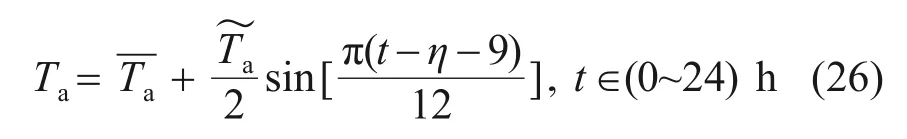
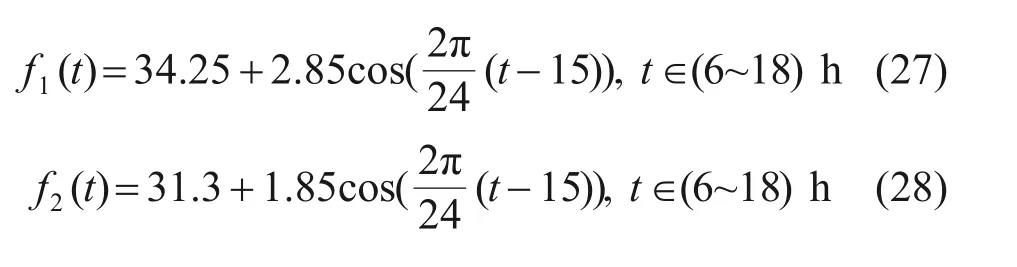
3.2 综合换热系数取值
采用式(29)计算箱梁中不同位置的综合换热系数:

箱梁外表面的风速为1 d 中实测风速的平均值;箱梁内的风速取v=0 m/s;hr利用式(3)计算。
文献[13]研究了综合换热系数对结构预估温度场的影响,发现1 d中综合换热系数为平均值时引起的温度计算误差不超过6%。2014−07−22的实测平均风速为2 m/s,按照上述方法进行计算可得到日照时长内换热系数平均值分别如下:轨道板表面的换热系数为20.7 W/(m2·K),箱梁内表面的换热系数为20.2 W/(m2·K),箱梁底板处的换热系数为11.7 W/(m2·K)。
3.3 方法验证
将定解条件代入式(24),得到箱梁−无砟轨道结构中不同位置(d1~d6)和箱梁底板不同位置(d7~d10)的温度级数解,并与有限差分法的数值解进行验证。结构温度的级数解与数值解如图5所示,其中,温度级数解用d表示,数值解用d′表示。
图5(a)所示为2014−07−22 太阳辐射时长内结构温度的级数解(级数展开式前8项求和的结果)和数值解的时程曲线,两者温度时空变化规律相一致。对比两者的温度波动特征发现:1)在太阳升起时刻(6:00),不同深度处(d1~d6)的温度计算结果均收敛于结构的初始温度;2)导热方程的级数解在非线性边界条件出现不收敛的情形[14],结构外表面(d1=0 m)温度的级数解与数值解的误差较大,最大绝对误差达到2.3 ℃。
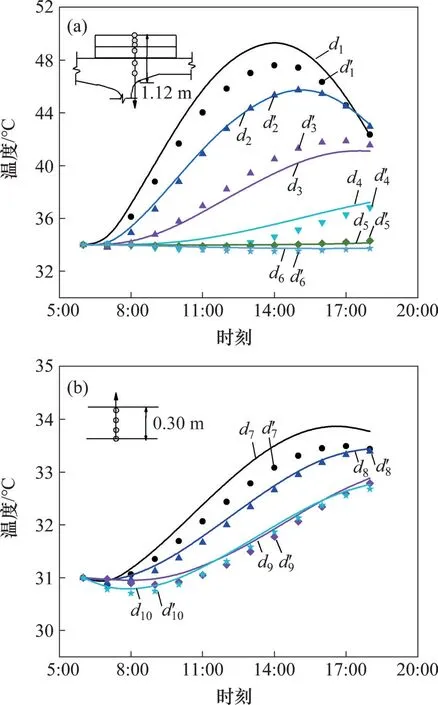
图5 结构温度的级数解与数值解对比Fig.5 Comparison between series solutions and numerical solutions of structural temperature
图5(b)所示为2014−07−22 太阳辐射时间内箱梁底板温度的级数解和数值解的时程曲线。从图5(b)可见:由于底板处无太阳辐射,边界的热流扰动很小,级数解和数值解的最大误差小于0.5 ℃,两者的时程曲线几乎重合,表明太阳辐射是影响混凝土温度场的主要因素。
经对比可知,箱梁−轨道结构温度场的级数解与数值解的最大相对误差小于5%,表明采用积分变换法求解箱梁−轨道结构温度场模型是准确、可行的。
3.4 计算结果与实测结果对比
图6所示为2014−07−22 太阳辐射时长内轨道板温度的实测值(T1~T4)和计算值(T′1~T′4)时程曲线。从图6(a)可见,由于温度预估模型的初始值高于实测值约2 ℃,致使特征点T′1和T′2的计算升温速率均比实测温度高;道床板内特征点T′1距轨道板表面0.05 m,其最高温度发生的时间保持一致,峰值温度的误差在1 ℃左右。从图6(b)可见:底座板距结构表面0.25 m,其温度时程曲线具有升温晚、温度波动小的特点,底座板内特征点(T′3和T′4)的温度计算值与实测特征点(T3和T4)的温度平均误差均为1 ℃左右。
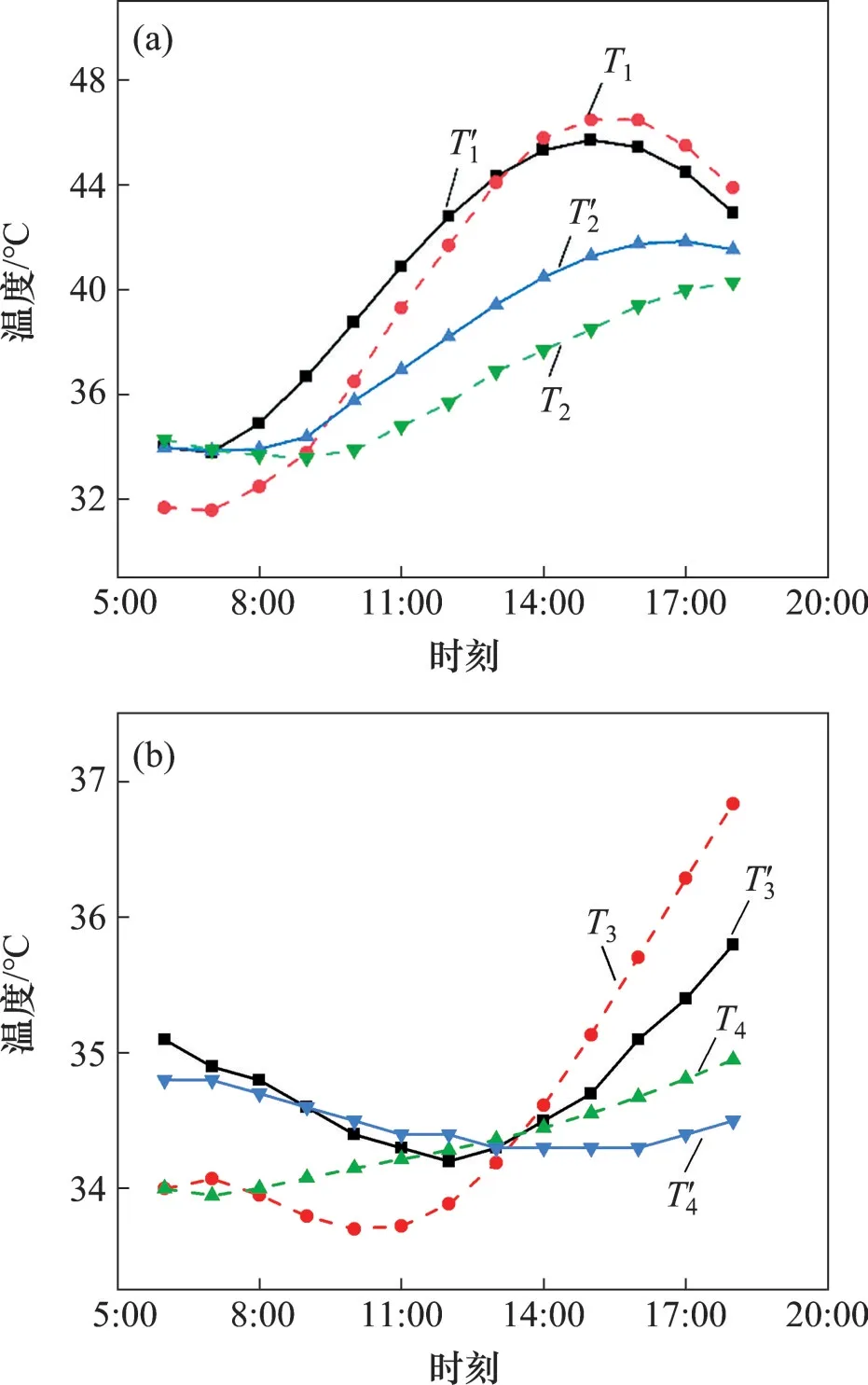
图6 结构温度的级数解与数值解对比Fig.6 Comparison between measured temperatures and calculation temperatures of ballastless track slab
经统计,实测温度与计算温度的最大相对误差为8%,可满足实际工程中结构的温度场分析及温度模式预测要求。
4 箱梁−无砟轨道升温模式的计算
4.1 轨道板表面温度的计算方法对比
轨道板中的温度测点距结构外表面的距离越小,对应的温度波动越大,如图6所示。日照时间内道床板中的温度波动幅值均在10 ℃以上,而底座板中温度测点距轨道板表面0.44 m,温度的波动幅值仅为0.5 ℃,由此假设:在日照时间内无砟轨道板表面的热扰动范围仅局限在轨道结构内,可按半无限大结构的温度场模型分析箱梁−无砟轨道结构温度场。
根据半无限大固体的一维非稳态温度场的解析解[16],同时忽略结构温度场中瞬态温度项的影响。当f1(t)>T(0,t)时,可得到结构表面温度的简化计算式:
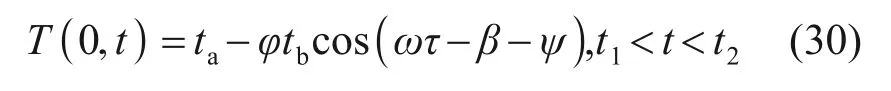
式中:ta和tb分别为结构表面流体温度的平均值和振幅;β为流体温度的相位;φ为结构表面温度与流体温度的振幅比值;ψ为结构表面温度相比流体温度滞后的相位角。
将流体温度函数式(25)的相关参数分别代入式(24)和(30),可求得不同温度场模型的表面温度计算值。日照时间内轨道结构表面温度的时程曲线如图7所示。从图7可见:由于日出后2~3 h 范围内,结构表面流体温度小于结构表面温度(f1(t) 图7 结构表面温度的计算结果对比Fig.7 Comparison of calculation results of structural surface temperature 新西兰规范[18]、美国AASHTO 规范[19]分别给出了混凝土结构竖向温度的五次抛物线形式和三折线分布形式。虽然规范中均考虑了不同铺装厚度(5~10 cm)对结构温差取值的影响,但既有温度模式对板厚近50 cm的箱梁−无砟轨道结构不适用。文献[15]通过对箱梁−无砟轨道板温度场进行长期测试与统计,发现在夏季高温时期,混凝土结构出现年最大正温差,可采用指数曲线描述结构竖向温度分布。 参考混凝土结构温度的三折线分布形式,利用2014年及2015年夏至日(15:00)的箱梁−无砟轨道结构的实测温度拟合结构最不利正温差,得到结构竖向温度的四折线分布形式,如图8所示。由于箱梁底板无太阳辐射,温度波动很小,距底板外表面0.15 m范围内的温差为1 ℃左右,因此,底板温度分布也采用折线表示。 同时,采用指数曲线拟合箱梁−无砟轨道结构的温度计算值,得到指数温度分布与实测温度、折线温度分布均比较接近,拟合度较高,如图8所示。利用2组实测数据计算得到道床板的温度梯度分别为80 ℃/m 和70 ℃/m,两者均小于中国高速铁路设计规范值90 ℃/m[1]。 图8 箱梁−无砟轨道结构竖向温度的拟合曲线Fig.8 Fitting curves of vertical temperature of box girderballastless track structure 结合箱梁−无砟轨道结构温度场的实测温度与计算温度,提出2种箱梁轨道结构的最不利温度分布曲线,如图9所示(其中,l为结构截面总高度;d为结构温度作用范围;ΔT1~ΔT4,ΔTu1,ΔTd1均为结构温度特征值)。图9(a)中,四折线分布形式需要4 个参数(ΔT1,ΔT2,ΔT3,ΔT4)才能确定,每个参数之间需按指定间隔距离取值;图9(b)中,指数分布形式仅需要3个参数(ΔTu1,ΔTd1和a),可适用于不同高度的结构截面,其函数形式为 图9 箱梁−无砟轨道结构的温度作用模式Fig.9 Temperature action model of box girder ballastless track structure 式中:ΔTu1和ΔTd1分别为结构截面上表面和下表面的温度特征值,其值分别为截面上、下表面温度与截面内部最小温度的差值;a为指数温度分布的衰减参数。 对于箱梁−无砟轨道结构的指数温度分布曲线,衰减参数a可利用结构温度计算结果拟合得到。由于温度级数解为时间t的变量,可计算出不同时刻的结构温度场分布;同时,对于不同截面高度,不同工况下的结构温度模式均可计算。相比于传统温度模式的计算方法[2−3],利用结构温度级数解可以得到不同环境参数、材料参数或截面高度的结构温度场分布。 表1所示为不同温度分布曲线的参数计算结果。由表1可知:1) 不同环境下结构表面的温度ΔT1取值不同;2)结构内的温度ΔT2~ΔT4几乎保持一致。在没有结构实测温度时,利用结构表面温度的级数解(式(24))或近似解(式(30))计算表面温度,ΔT2~ΔT4可按照表1取值。 表1 不同温度模式的计算结果对比Table 1 Comparison of calculation results of different temperature models 1)结合实桥温度与气象参数建立了第三类边界条件的箱梁−无砟轨道结构温度场的预估模型,采用积分变换法求得了太阳辐射时长内结构温度场模型的级数解。 2)箱梁−无砟轨道温度场的级数解可由级数展开式前8项求和近似得到,与数值解的最大相对误差为5%,与实测数据的最大误差为8%。混凝土结构温度场的级数解可适用于不同截面高度、不同时刻的结构温度预测。 3)当等效辐射气温大于混凝土结构表面温度时,有限域结构的表面温度级数解与半无限域结构的表面温度近似解的计算误差在1 ℃之内,可采用结构温度的近似解快速计算结构表面温度。 4)高速铁路箱梁−无砟轨道结构的四折线温度分布曲线和指数温度分布曲线与实测温度分布曲线拟合度高。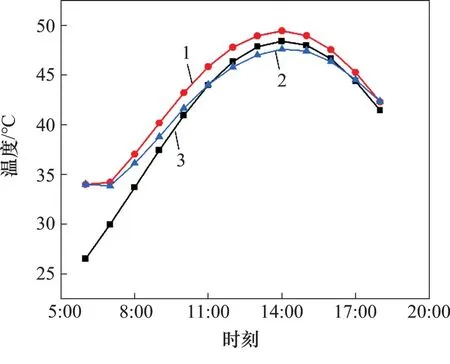
4.2 箱梁−无砟轨道温度模式的拟合结果
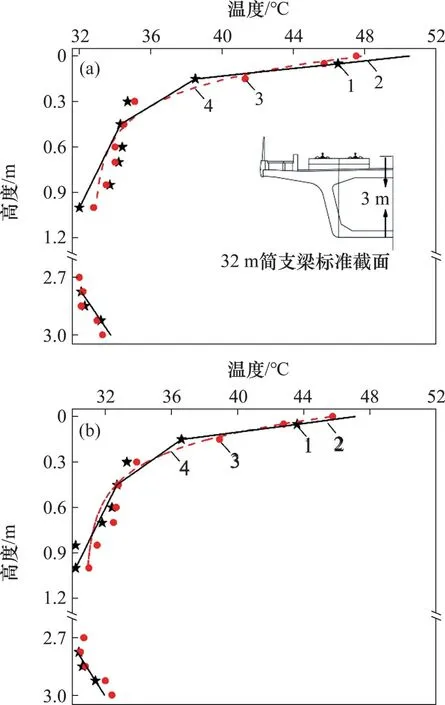
4.3 箱梁−无砟轨道升温模式的参数计算
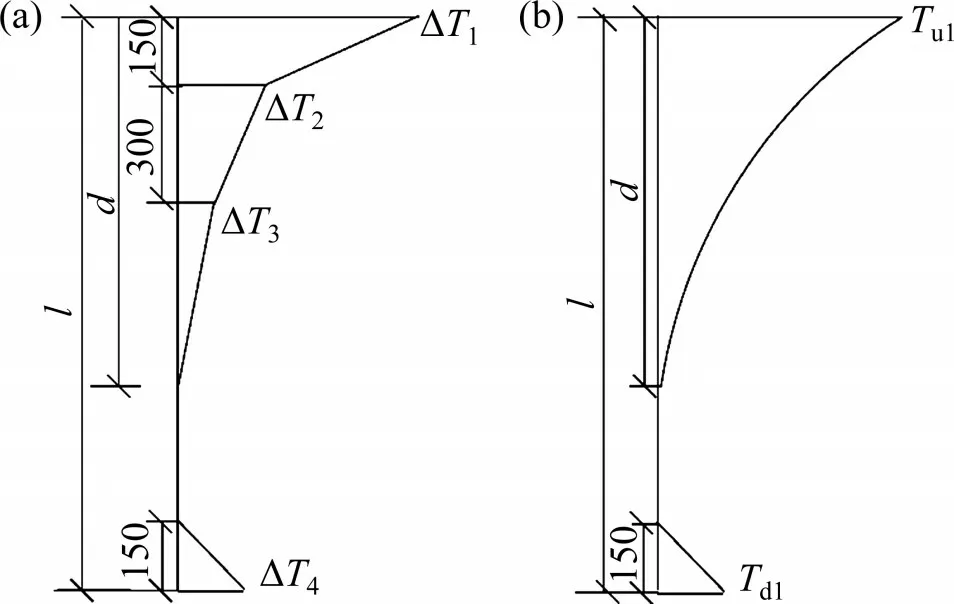
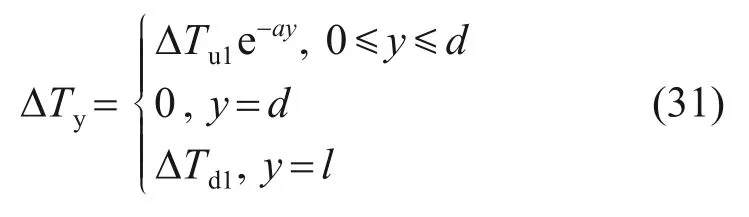
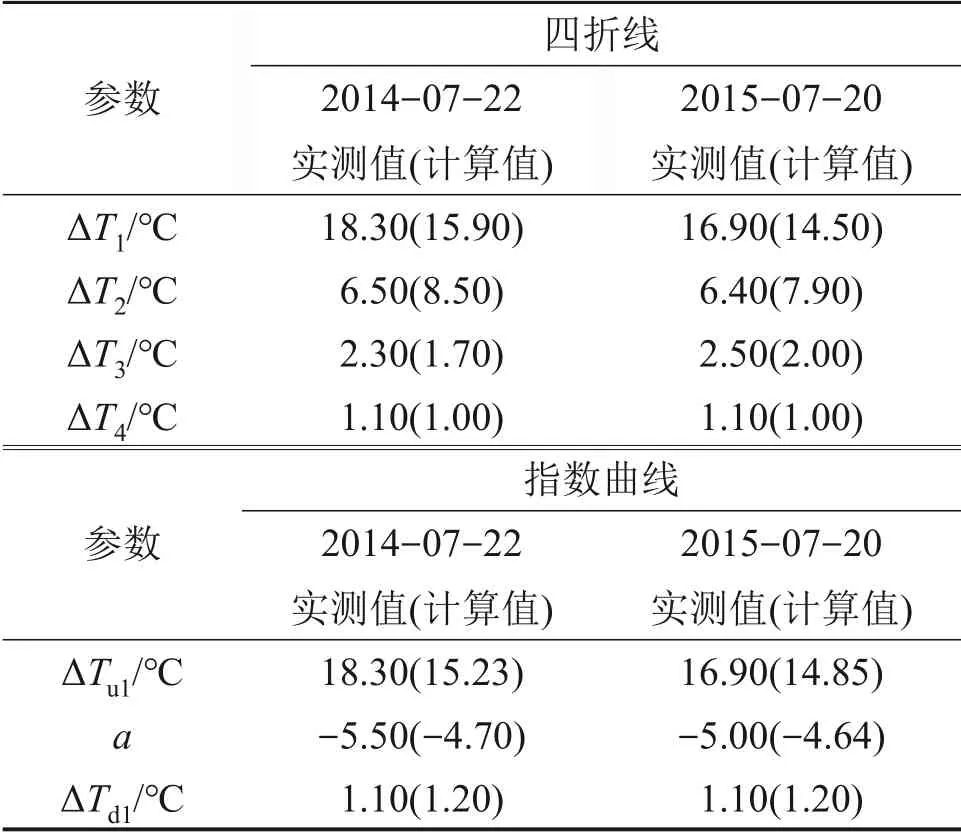
5 结论

