基于最小二乘法的电子电路功率器件故障诊断方法

顾 雄

（六盘水职业技术学院，贵州 六盘水 553000）

0 引 言

近几年，电子电路被应用到了更多信息安全设备上，其工作状态会直接影响设备运行稳定性。因此，针对电路故障诊断技术的研究，成为当前该领域研究人员重点关注的话题[1]。同时，研究人员在研究的过程中，还将提升设备运行维护水平等内容作为了重要的研究课题。由于电子电路具有非线性特征，并且所连接的各类元器件存在参数容差性、故障类型多样性的特点，因此使得现有故障诊断方法在应用对电子电路功率器件的故障诊断中常常会出现自身局限性问题或故障诊断准确率低的问题[2]。

为了解决这一问题，本文借助最小二乘法的实时性和鲁棒性，设计电子电路功率器件故障诊断方法，以期提高诊断准确度，为电子电路功率器件稳定运行提供技术支持。

1 电子电路功率器件故障特征量采集与预处理

在对电子电路功率器件的故障问题进行诊断时，需要从器件在运行过程中的状态信息量当中，采集器件故障特征量。当电子电路功率器件出现故障问题时，无论是哪一种故障类型，其特征参数都会发生改变，因此为体现诊断的全面性，选择将电子电路输入电压、输出电压、输入电源、输出电源等作为故障诊断中所需的电子电路功率器件故障特征量[3]。针对上述各个参数变量进行实时监测，同时上述获取到的参数也是后续故障诊断模型的主要输入变量。由于电子电路功率器件故障参数存在于不同量纲和数量级上，因此为了避免在后续诊断中出现病态情况，对特征量进行预处理。按照公式进行归一化处理即：

式中：yi表示经过归一化处理后得到的电子电路功率器件故障特征数据结果；xi表示原始电子电路功率器件故障特征数据；min(X)表示故障特征数据集合中的最小数值；max(X)表示故障特征数据集合中的最大数值。按照上述内容，完成对电子电路功率器件故障特征参数的预处理。

2 基于最小二乘法的器件故障诊断模型建立

针对上述经过处理的故障特征量进行故障诊断，引入最小二乘法，完成对器件故障诊断模型的建立。将特征量作为输入变量，将其输入到经过训练后的最小二乘法模型的输入端，并通过核运算输出故障类别。图1为最小二乘法基本结构。

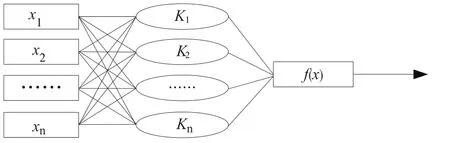
图1 最小二乘法基本结构图

图1中K表示最小二乘核函数。利用具有上述结构的最小二乘模型，对输入变量识别进行泛化学习。为促进故障诊断效率和正确率的进一步提升，在上述最小二乘法基本结构当中引入一个针对电子电路功率器件故障诊断的分类器[4]。针对具有两种不同模式分类的诊断问题，通过运算将两类间隙最大的最优超平面求解问题，转变为二次规划问题，其表达式为

式中：minJ(w,ξ)表示最优目标函数；wT⋅w为两个特征变量之间的内积；c表示可调节的参数；ξ表示诊断误差。在上述公式基础上，结合拉格朗日函数，对公式（2）进行转换，其表达式为

式中：b表示判决函数；α表示拉格朗日乘子。将上述表达式作为分类器，将其应用到上述最小二乘法基本结构当中。在实际应用上述建立的模型结构对电子电路功率器件故障问题进行诊断时，可采取一对一或一对多的方式对多种故障类型进行诊断。将每一个类别当中所有采集到的特征样本和其他类型特征样本进行一对一或一对多的比较，并在上述分类器的基础上，再次构建二值分类器，每一个分类器在实际应用前都需要进行训练。共完成对k（k-1）/2个分类器的构建，其中k表示电子电路功率器件故障类型的具体数量。将需要进行故障诊断的特征变量输入到k个故障类型中的n个类型中的第m个类别二值分类器当中。若输出的结果判定该被诊断的特征量属于m类，则给m类的票数加1，反之，若输出的结果判定该被诊断的特征量属于n类，则给n类的票数加1。通过上述思路，可实现对电子电路功率器件故障的诊断，但上述操作会使得模型的复杂程度增加。因此，针对这一问题，为实现更高效和更高精度的诊断，将径向基函数（Radial Basis Function，RBF）带入到上述构建的诊断模型当中。RBF中包含的参数较少，并且数据限制条件也较少，因此通过对这一函数的应用能够在训练过程中提升故障诊断的训练速度，从而达到大大降低诊断模型复杂性的目的。RBF函数的表达式为

式中：K（x,xi）表示x与xi的最小二乘核函数；σ表示取值为正的实常数。将式（4）带入到电子电路功率器件故障诊断模型当中，并将最终得到的结果作为后续对器件故障二值分类诊断的模型。

3 器件故障二值分类诊断

在完成对基于最小二乘法的器件故障诊断模型构建后，还需要解决模型当中二值分类器在应用到电子电路功率器件故障诊断中的适应性问题。为了能够保证电子电路正常、平稳地运行，对故障诊断方法提出了不仅需要及时判断出电子电路功率器件是否存在故障问题，同时还需要确定出现故障问题时，具体故障位置等相关信息[5]。因此，在故障状态判别的基础上，形成了多值分类问题。在对某一分类器i构建时，将属于该类别的最小二乘法故障训练样本作为一种类型，并将其原有标记从“i”改为“1”，并将其他各个故障类型均按照上述方式进行标记，根据具体情况标记可选择“1”或“-1”。在具体操作时，将需要进行故障诊断的特征样本输入到二值分类器1当中，并判断其输出结果是否为1。若为1，则将其故障类型设置为1；若不为1，则将特征样本输入到二值分类器2当中，并同样判断其输出结果是否为1。若为1，则将其故障类型设置为2；若不为1，则将特征样本输入到下一个二值分类器3当中，以此类推，直到最终判定结果为1时，确定该故障特征变量的具体故障类型。在这一过程中，还需要结合小波变换的方式，对输入的故障特征变量进行优化，并完成对特征样本的构建。小波变换的表达式为

式中：vg表示经过小波变换后的故障特征变量样本；vsk表示在进行小波变换前的故障特征变量样本；kθ表示正弦谐波幅值。按照上述公式完成对故障特征变量的转换后，根据电子电路功率器件每种类型的故障特征，为最小二乘法二值分类器建立多个训练样本。当被识别的特征量样本为i故障类型时，则将其二值分类器的数值设置为1，否则将其设置为-1。最终为每一种电子电路功率器件故障类型划分一个对应的二值分类器，结合分类器输出结果实现故障诊断。

4 对比实验

在完成对故障诊断方法理论的设计后，为进一步验证这一方法的实际应用可行性以及与其他诊断方法相比所具备的应用优势，选择以某正弦信号发生器电路为研究对象，针对该电路上的功率器件故障问题，分别利用本文诊断方法和基于ARPSO的诊断方法对其进行故障诊断。为方便后续论述，将本文提出的诊断方法设置为实验组，将基于自适应粒子群优化算法（Attractive and Repulsive Particle Swarm Optimization，ARPSO）的诊断方法设置为对照组。实验过程中，将该电子电路中电阻和电容容差分别设置为10%和20%。为实现对故障诊断精度的检验，在利用两种诊断方法进行对该实验对象的故障诊断时，按照表1所示的内容，设置已知的故障模式。

表1 电子电路功率器件故障参数设置

按照表1中的内容完成对电子电路功率器件故障参数的设置，在此基础上，对比两种故障诊断方法诊断结果与实际故障，在针对每一故障代码下对应故障类型完成200次诊断后，计算200次诊断结果的诊断准确率，其公式为

式中：μ表示诊断方法的诊断准确率；F表示实验前设置的某一故障类型出现次数；F'表示利用诊断方法诊断出的故障类型出现次数。根据上述公式，完成对两种诊断方法诊断准确率的计算，计算得出的μ值越高，则说明该诊断方法的诊断准确率越高，诊断结果越符合实际；计算得出的μ值越低，则说明该诊断方法的诊断准确率越低，诊断结果越不符合实际。根据上述论述，对两种诊断方法诊断准确率进行计算，并将结果绘制成如图2所示的对比图。

图2 实验组与对照组诊断方法诊断准确率对比图

从图2可以看出，实验组诊断方法的诊断准确率均在85.00%以上，而对照组诊断方法的诊断准确率仅在50.00%～60.00%内波动，明显实验组诊断方法的诊断准确率更高，进而说明其诊断精度更高，针对结果更符合实际。

5 结 论

本文旨在明确电子电路功率器件故障发生原因以及器件在正常运行时的基本特征后，在引入最小二乘法的基础上，提出了一种全新的故障诊断方法，通过对比实验的方式验证了新的故障诊断方法与基于ARPSO的诊断方法相比，诊断准确率更高，诊断结果更符合实际电子电路功率器件故障情况。在后续研究中，将以器件故障状态的分辨率提升为目标，开展更深入的探索和研究。