基于指数归一化欧式距离的架空线-电缆混合线路故障区段定位方法

国网吉林省电力有限公司四平供电公司 刘 刚 贾克音 王功臣 冀 石 刘俊峰 郑世洋 张 莹

随着馈线自动化广泛应用，通过馈线终端(Feeder Terminal Unit，FTU)或者故障指示器可以获得配网故障暂态零模电流信号[1]，并利用先进的信号处理技术提取故障特征，有力推动了配网故障区段定位技术发展。依据暂态零模电流相似性；文献[2]提出了能量谱法，并通过自适应聚类分析确定故障区段，该方法复杂度高，耗费算力。

文献[3]从信号距离角度提出了动态时间弯曲(Dynamic Time Warping，DTW)距离法，其算法简单，降低了对数据量和同步要求，但应用于架空线-电缆混合线路时，由于非故障电缆线路两端暂态零模电流差异大，易导致误判，下文称之为定位盲区；文献[4]提出了基于暂态零模电流衰减速度比的绝对值与极性的混合线路故障区段定位方法，该方法需要提取特定频段内的暂态分量，而频段选取受故障点位置和网络结构参数影响。

为消除架空线-电缆混合线路故障区段定位盲区，兼顾算法简单，提出了基于指数归一化欧式距离的混合线路故障区段定位方法。首先，分析混合线路单相接地故障上下游暂态零模电流特征；其次，介绍基于指数归一化欧式距离的故障区段定位原理；最后，通过MATLAB/Simulink 仿真验证该方法的有效性。

1 单相接地故障暂态零模电流特征

图1所示为简单的架空线-电缆混合配电网。在主谐振频段范围内，其简化的单相接地故障暂态等值电路由线模和零模网络Γ 形等值网络组成如图2所示[5]。

图1 简单的架空线-电缆混合配电网

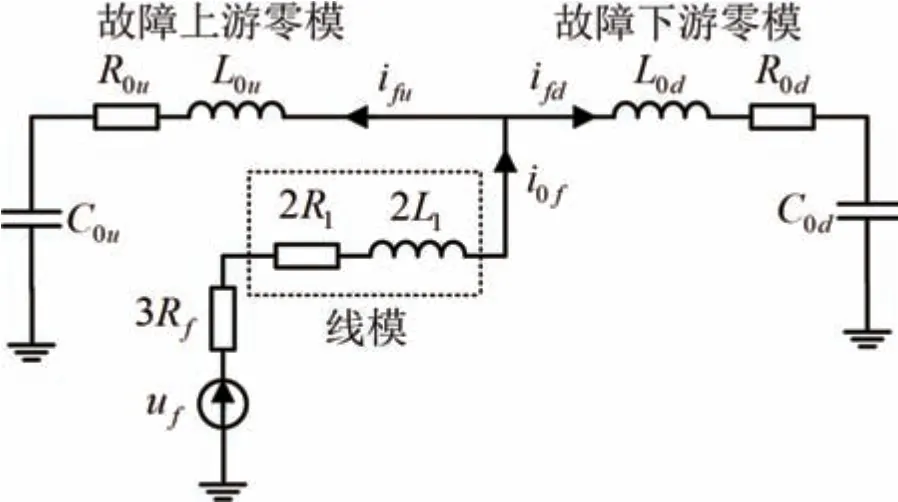
图2 单相接地故障暂态等值电路

图2中L1、R1分别为线模电感和电阻；R0u、L0u、C0u分别为故障上游零模电阻、电感和电容；R0d、L0d、C0d分别为故障下游零模电阻、电感和电容；Rf为过渡电阻；i0f、ifu、ifd分别为故障点和故障上下游零模电流；uf为虚拟电源。各参数计算如下所示：

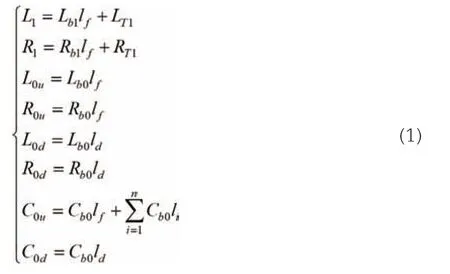
式中：Rb1、Lb1分别为单位长度线路线模电阻和电感；Rb0、Lb0、Cb0分别为单位长度线路零模电阻、电感和电容；lf为故障点到母线的距离；ld为故障下游长度；li为第i 条健全线路长度。由图2可得，故障上下游转移导纳Hu=ifu/uf和Hd=ifd/uf如式(2)所示。计算出Hu、Hd的极点及其单位阶跃响应su(t)、sd(t)，便可以定性分析故障上下游暂态零模电流特征。

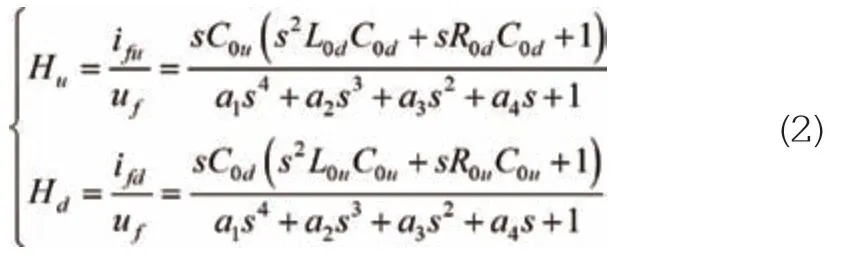
式中：

以图1中馈线L3发生单相接地故障f4为例，由式(1)～(2)计算出不同lf和Rf的Hu、Hd的极点和su(t)、sd(t)，见表1和表2。表1中，Rf=10Ω 时，三个位置的Hu(或Hd)的极点均为两对共轭复根，则故障上下游暂态零模电流含有两个不同衰减速度和振荡频率的分量，且两分量的幅值比例不同；同一对共轭极点对应的上下游分量在幅值或相位上存在差异。表2表明Rf较大时，lf=1.5km 的Hu(或Hd)的极点为一对共轭复根和两个负实根，则故障上下游暂态零模电流主要是一个振荡衰减分量，下游分量的幅值接近上游的2倍。

表1 Rf=10Ω，不同lf 的Hu、Hd 的极点与su(t)、sd(t)

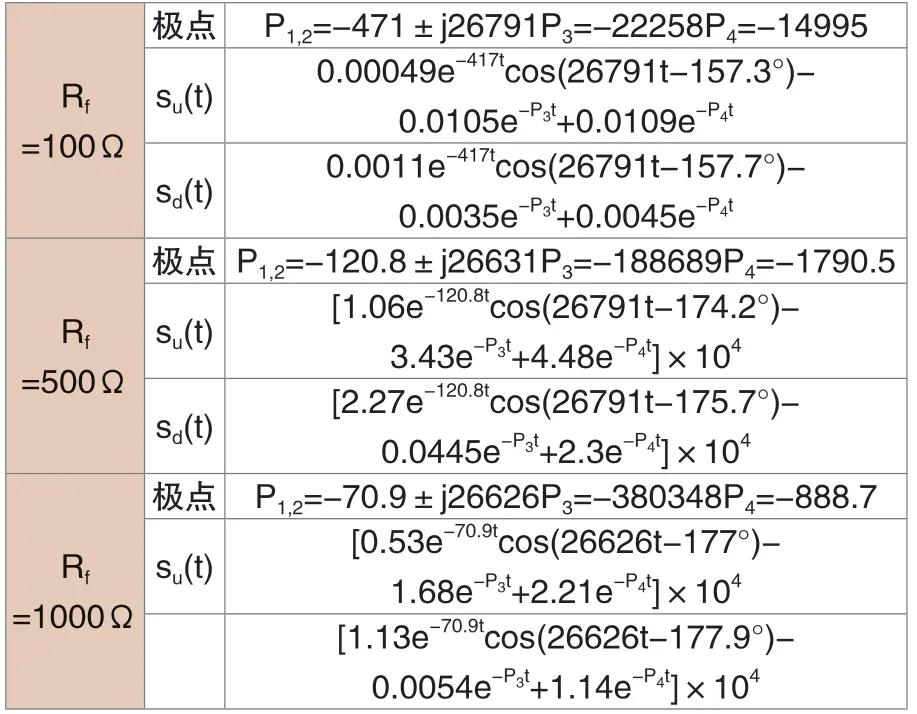
表2 lf=1.5km，不同Rf 的Hu、Hd 的极点与su(t)、sd(t)

2 基于指数归一化欧式距离的故障区段定位方法

2.1 指数归一化欧式距离

不同线路的暂态零模电流幅值变化范围大，导致信号距离大幅变化，不利于设定固定阈值判据，故需先对信号距离进行特征缩放。常用的特征缩放方法包括最值归一化和零均值标准化。前者可能存在过度缩放，而后者的缩放比例综合了所有样本点影响。另外，混合线路的暂态零模电流波形复杂，曼哈顿或欧式距离所表征的低次差异特征很可能相近。为挖掘新的特征，引入了信号距离d 的自然指数函数归一化变换f(d)，如式(3)所示，其具有如下性质：ex可展成泰勒级数，则f(d)等价于无穷多个d 的各次幂项加权，既获得d 的高次特征，又避免高次项直接计算；f(d)随着d 增大而单调递增，并映射到[0,1]。

综上，将零均值标准化与f(d)相结合，构造出指数归一化欧式距离。设相邻FTUx 和FTUy 的零模电流序列分别为i0x={i0x1,i0x2,...,i0xN}，i0y={i0y1,i0y2,...,i0yN}，则i0x和i0y之间指数归一化欧式距离的定义如式(4)所示，记作dxy_e。

式中：σ 为带宽，其数值由i0x-i0y的标准差确定；||i0x-i0y||为i0x与i0y之间欧式距离。i0x和i0y之间最值归一化DTW 如式(5)所示，将其记作dxy_DTW，以便同dxy_e进行对比。式中：规整路径P={p1,p2,...,pr}；元素pk表示路径上第k 点的坐标，即pk=(i,j)，对应的点距离d(pk)=|i0xi-i0yj|。

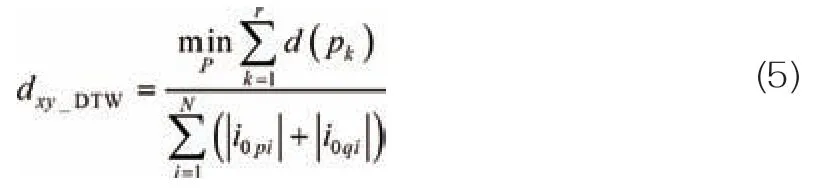
2.2 幅值、极性和频率差异对指数归一化欧式距离的影响

为初步验证dxy_e的性能，先模拟单一特征频率的暂态零模电流。设参考电流序列i0r与测试电流序列i0t分别为：

式中：kA表示幅值比和极性关系；kf为频率比；采样时刻t=[0:0.0002:0.0048]s。

根据零模电流分布特点，0＜kA＜1时，i0r和i0t可代表同侧零模电流；kA＜0时，i0r和i0t可代表异侧零模电流。kf可代表不同主谐振频率。将式(6)代入式(4)和式(5)，得到drt_DTW与drt_e关于kA和kf的关系曲线如图3所示。

图3(a)中，不同kf的drt_DTW-kA关系曲线规律一致，在分界点kA=0，drt_DTW恒为最大值1，分界点的左侧总体呈V 形，而右侧单调下降。kA＜-2的drt_DTW变化规律表明故障点的异侧幅值和频率差异越大，drt_DTW越大。显然，分界点两侧很可能出现drt_DTW相近的情况而无法判定故障区段；图3(b)中，当kA＜0，不同kf的drt_e沿kA正方向单调递减，且随着kf远离1而小幅下降，如kf=1和kf=0.2之间偏移最大位置为kA=-1.4，drt_e由0.6101下降至0.4857。0＜kA＜1且0.933＜kf＜1.067范围的drt_e小于kA＜0范围的drt_e，保证故障异侧的drt_e大于故障同侧，有效消除了定位盲区，所以适应性优于drt_DTW。

图3 i0r 和i0t 取不同kA 和kf 的drt_e 与drt_DTW

2.3 故障区段定位方法

基于指数归一化欧式距离的混合线路故障区段定位流程如图4所示。首先，采用暂态零模电流群体比幅比相法进行故障选线[3]。然后，计算故障馈线上各区段两端暂态零模电流的dxy_e，其中最大值对应的区段判定为故障区段。

图4 故障区段定位流程图

3 仿真验证

为验证所提出的混合线路故障区段定位方法的有效性，搭建了图1的MATLAB/Simulink 仿真模型。其中架空线和电缆正序和零序参数见表3。仿真步长为1μs，采样频率为5kHz。分别在分段线路的中点f1～f4处设置A 相单相接地故障，且故障初相位为60°、过渡电阻为10Ω。取故障前5ms 和故障后15ms 的暂态零模电流仿真数据，计算dxy_e(i0x,i0y,σ=40)与dxy_DTW(i0x,i0y)。

表3 架空线和电缆正序和零序参数

图5为故障f4对应的FTU7～FTU9的暂态零模电流响应曲线。观察FTU7与FTU8的暂态零模电流波形，两者幅值接近、极性相反，主谐振频率不同，其中小窗口为截取故障后5ms 的暂态零模电流波形和图2等值电路计算的零状态响应ifu、ifd。各小窗口中的两个响应曲线的重合度较高，由此表明FTU7与FTU8的暂态零模电流波形的衰减特性与振荡频率规律与第1节的理论分析保持一致。相邻的下游非故障电缆线路两端FTU8与FTU9的暂态零模电流的极性相同，主谐振频率接近，而幅值差异较大。结合图3(a)，此时可以初步判断故障f4易处于DTW 法的定位盲区。

图5 故障f4的暂态零模电流响应曲线

表4为混合线路发生故障f1～f4对应的dxy_e与dxy_DTW以及故障定位结果。由表4可见，在定位故障f1（或f4）时，相邻非故障电缆区段(FTU3,FTU4)（或(FTU8,FTU9)）的dxy_DTW稍高于故障区段，dxy_DTW法产生了误判，由此表明dxy_DTW法在混合线路故障定位中存在定位盲区。dxy_DTW法失效的原因在于电缆线路对地电容较大，导致非故障电缆区段两端的暂态零模电流之间幅值差异大，此时它们的dxy_DTW很可能靠近1.0而超过故障区段。相反，故障f1～f4所在故障区段的dxy_e均显著高于非故障区段，准确识别出故障区段，反映出dxy_e在综合表征故障暂态零模电流之间幅值、极性与频率差异的优势。因此，所提出的dxy_e法有效消除了混合线路的故障定位盲区，且适应性良好。

表4 故障定位结果

表5为故障f1在不同故障初相角和过渡电阻情况下，馈线L2各区段的dxy_e 值。由表5可见，在0°～90°，故障初相角越大dxy_e值越大。相同故障初相角，过渡电阻越大dxy_e值越小。当过渡电阻≥500Ω 时，故障初相角对dxy_e值的影响很小。对不同故障初相角和过渡电阻，尤其在高阻接地时，故障区段的dxy_e值都大于非故障区段，进一步反映了dxy_e法的适应性较强。但需注意高阻接地时故障暂态零模电流幅值显著减小，不利于故障信号检测。因此，高阻接地故障准确识别仍有待下一步研究。

表5 故障f1在不同故障初相角和过渡电阻的dxy_e

综上，本文提出了一种基于指数归一化欧式距离的架空线-电缆混合线路故障区段定位方法。相比动态时间弯曲距离法，指数归一化欧式距离不仅综合反映了相邻暂态零模电流差异的低次和高次特征，而且保证故障区段的特征值显著高于非故障区段，有效消除了架空线-电缆混合线路故障定位盲区，实现准确识别故障区段。