质量放大系数对三代轮毂轴承旋压铆合仿真的影响

梁天,董绍江,2,朱孙科,赵兴新,李洋,潘雪娇,蒙志强,朱朋

(1.重庆交通大学机电与车辆工程学院，重庆 400074；2.磁浮技术与磁浮列车教育部重点实验室，四川成都 610031； 3.重庆长江轴承股份有限公司，重庆 401336)

0 前言

三代轮毂轴承(见图1)目前在轿车领域运用广泛，是汽车关键零部件之一。相比于传统轮毂轴承通过螺母将内圈、外圈、滚珠、保持架固定在一起，三代轮毂轴承通过旋压铆合工艺将各个零件固定在一起，结构更紧凑、节约了空间、降低了质量。目前，为探究该工艺主要运用有限元仿真的方式。由于三代轮毂轴承具有结构复杂、接触对较多、收敛困难的特点，主要采用处理高度非线性动力学问题能力更强的显式算法进行仿真。

图1 三代轮毂轴承

许多学者对三代轮毂轴承的旋压铆合工艺进行了有限元仿真分析。肖耘亚等去掉保持架等非关键零件，并将滚珠、外圈等零件设置为刚体，以缩短计算时间，分析了铆装力、翻边的形状以及内圈的外径变化。杨军等人仅考虑了压头、大小内圈进行旋压铆合仿真，分析了压头倾角、保压时间、压头轨迹等因素对三代轮毂轴承的影响。李雪原等仅对小内圈和芯轴进行旋压铆合仿真，分析了在不同倾斜角度下，压头受到的轴向力和内圈卡紧力。汪浔建立了考虑两个内圈和法兰轮毂的接触模型，进行了轮毂轴承的刚性分析。牛荣军等利用有限元软件，仿真分析了仅包含轴端部位和小内圈的旋压铆合工艺，分析了该部位应力和应变的特性。由于显式算法具有计算增量步极小的特点，对旋压铆合工艺实际需要的时间较长，仿真难度极大。上述文献中，对于旋压铆合工艺的仿真主要是针对大小内圈部分的分析，未考虑其他零件为弹性体的情况。

李文亚等分析了质量放大系数对搅拌摩擦焊接插入过程的影响。利用质量放大系数，大大减少了仿真计算时间，提高了工作效率。有限元仿真分析是针对三代轮毂轴承旋压铆合工艺的重要研究方法。但是，由于旋压铆合工艺的实际工作时长、三代轮毂轴承结构特点和工作特点，其仿真耗时极长。本文作者通过仿真分析不同质量放大系数下的旋压铆合加工，对比分析三代轮毂轴承小内圈外径膨胀量、翻边外径的差值、铆装力情况、小内圈的受载特点和整体应力分布情况，探讨质量放大系数对三代轮毂轴承旋压铆合工艺的影响，确定合适的质量放大系数。

1 数学模型

1.1 模型参数和边界条件

在ABAQUS中建立三代轮毂轴承三维模型，考虑到计算量巨大，忽略部分次要零件。在旋压铆合工艺中，滚珠相对运动较小，保持架起到隔开作用，受到的载荷较小，则将保持架设置成刚体，且仅保留与滚珠接触的兜孔和连接兜孔的部位。滚珠的接触复杂，在滚珠切割后网格质量较差，对计算速度影响极大，但滚珠的接触载荷等极为重要，保留为弹性体。压头刚度相对于其他零件而言较大，故设置为刚体。最终保留为弹性体的有滚珠、大内圈、小内圈、外圈，建立三代轮毂轴承有限元网格模型如图2所示。各零件的材料属性如表1所示。同时，对大内圈翻边部位设置塑性材料属性。

图2 三代轮毂轴承有限元网格模型

表1 第三代轮毂轴承单元零件材料属性

根据实际加工条件，将大内圈的法兰盘端面固定，对压头设置合适的进给速度和旋转速度。在此次仿真中，为保证旋压铆合工艺的合理性，进给量相对于理论厚度增加了0.2 mm，以保证翻边与小内圈贴合。各个零件通过接触关系相互连接，滚珠与保持架的接触设置为无摩擦接触，滚珠与内外沟道、压头与大内圈之间的摩擦因数设为0.12。

旋压铆合工艺进给时间为6 s、保压时间为0.2 s，并考虑在仿真中存在的振动对参数提取的影响，将回退和静置时间设置为3.8 s，则仿真总时长共10 s。对于以极小稳定增量步计算的显式求解器而言，该工艺仿真耗时极长，亟需一种可以缩短分析时间的方法，故应适当地考虑质量放大系数。

1.2 质量放大系数

在实际加工中，旋压铆合工艺的时间虽然仅有6.2 s，但是在显式动力学仿真时，由于某结构复杂、网格尺寸限制以及显式求解时间增量步极短，导致仿真耗时极长，不能在较短时间内得到合适的结果。质量放大作为一种能够不需要人为提高旋压铆合进给速度以减少仿真时间的方法而被考虑。最小稳定时间增量Δ计算公式为

(1)

式中：为模型最小单元长度；为材料的膨胀波速。在三代轮毂轴承的旋压铆合工艺仿真中，初始时网格最小单元尺寸出现在滚珠上。对于线弹性材料，膨胀波速为

(2)

式中：为材料的弹性模量；为材料的泊松比；为材料的密度。当材料的密度增加时，材料的膨胀波速降低到原来的1/2次方，随之，最小稳定时间增量增大到原来的1/2次方。在质量增大后，由于惯性增大，仿真的结果也会受到影响，故需要考虑适当的质量放大系数。

2 仿真结果分析及讨论

采用Intel core i9 10900X(3.7 GHz、10核心、20线程，文中仿真为避免死机仅用19线程)进行旋压铆合仿真，在没有考虑质量放大系数的情况下，模型大概要计算20天，计算时间极长，不能用于多种工况的分析以及对旋压铆合工艺和三代轮毂轴承结构的优化。在质量放大系数达到10时，模型由于惯性过大会出现过度扭曲、报错。分别在质量放大系数为10、10、10、10、10时进行仿真，得到不同质量放大系数下，旋压铆合仿真工艺仿真总时长如图3所示。可知：在质量放大系数为10时，仿真总时长为28.63 h;在质量放大系数在10以后时，仿真时间变化减小，且耗时仅几个小时。

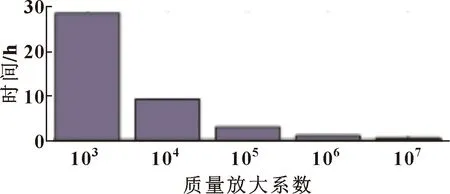
图3 不同质量放大系数下仿真耗时

2.1 质量放大系数对小内圈轴向位移的影响

在不同质量放大系数下，对小内圈在旋压铆合工艺过程中的位移进行研究，结果如图4所示。小内圈在旋压铆合前期，由于受到压头的冲击，产生振动，向上爬升；在旋压铆合后期，由于翻边变形量增大，对小内圈产生下压作用，故出现明显的下降，该过程与文献[2]中现象一致。

图4 不同质量放大系数下小内圈轴向位移随时间的变化

在压头回退一端后，小内圈稳定处于一个位置，文中将该位置作为小内圈最终的位移量。经分析发现，除质量放大系数为10外，在6.3～6.5 s时，该值趋于稳定，后续可缩短回退及静置仿真时间，进一步提高计算速度。研究不同质量放大系数下的小内圈的位移量，可知：小内圈最终的位移量随着质量放大系数增大，逐渐从负值变成了正值；在质量放大系数为10和10时，小内圈的位移量分别为-0.012 882 9、-0.010 564 2 mm，即在相应压头进给量作用下，小内圈下降，滚珠和沟道存在挤压，产生了负游隙。

2.2 质量放大系数对小内圈外径膨胀量的影响

小内圈在旋压铆合加工过程中会发生径向膨胀，这样的膨胀对三代轮毂轴承的寿命影响巨大。在不同质量放大系数下，在小内圈的外径处取若干个点(文中在取翻边和小内圈各点时，由于取点困难，仅相对均匀地间隔取点，未完全实现同编号为同一点)，分析其径向膨胀量，结果如图5所示。

图5 不同质量放大系数下小内圈外径膨胀量

由图5可知:其小内圈外径的膨胀量均小于实际加工的三代轮毂轴承的外径膨胀量的最大值；但是，与实际测得的最小值对比时，仅有质量放大系数为10和10时仿真所得到的各点的小内圈外径膨胀量比实际测得的最小值高；对比不同质量放大系数下的小内圈外径膨胀量，质量放大系数越小，各点处测得的小内圈外径膨胀量波动越小，故可以考虑采用较小质量放大系数来进行仿真。综合对比，质量放大系数为10和10时的小内圈外径膨胀量更合适。

2.3 质量放大系数对翻边外径的影响

将利用不同质量放大系数仿真得到的翻边外径减去装配名义尺寸，并与公差比较，结果如图6所示。由于进给量设置较大，故翻边外径的差值更接近上极限偏差。对比不同质量放大系数仿真得到的翻边外径差值，发现仅有质量放大系数为10时，翻边外径差值平均值为0.017 mm，其平均值和所取各值总体在公差范围之内。而质量放大系数为10和10时，靠近上极限偏差，平均值分别为0.022、0.023 mm。在分析模型网格后，认为翻边部位的网格尺寸较大是原因之一。同时，质量放大系数增大，导致的惯性增大也可能是另一个原因。当质量放大系数过大时，翻边外径已经远离上极限尺寸。

图6 不同质量放大系数下翻边外径

2.4 质量放大系数对铆装力的影响

将压头受到的反作用力的轴向分力作为铆装力。由于=6.2 s以后压头与翻边部位分离，压头不受任何载荷作用，故仅对0～6.2 s进行分析，结果如图7所示。可知：在0～6 s时，压头处于旋铆阶段，随着压头与翻边处的金属流质接触面积增大;铆装力逐渐增大;在6～6.2 s时，压头处于保压阶段，由于翻边部位发生塑性变形且最终定形，铆装力逐渐减小至定值；在6.2～6.3 s时，压头回退，脱离与翻边的接触，铆装力逐渐消失，趋近于0。

图7 不同质量放大系数下的铆装力

总体上看，对于不同的质量放大系数，在整个旋压铆合过程中，铆装力基本差别较小，这可能是因为虽然有惯性力作用，但是压头本身的运动轨迹是固定的，大内圈的自由度也在法兰盘部位受到限制，没有设置其余速度、载荷等边界条件和释放边界条件，故质量放大系数对铆装力影响相对较小。

2.5 质量放大系数对整体应力和小内圈轴向载荷的影响

在旋压铆合加工中，翻边部位受到的挤压最大，故应力在该部位集中，如图8所示。如图8(a)、(b)所示，在与小内圈倒角接触的翻边部位应力最大，故该部位是主要的受载部位，为小内圈提供主要的轴向卡紧力。对比分析不同质量放大系数下的应力，可知在质量放大系数为10和10时，三代轮毂轴承的应力分布较接近，其中最大等效应力分别为501.6、498.5 MPa；其余质量放大系数应力下，三代轮毂轴承应力差别巨大。

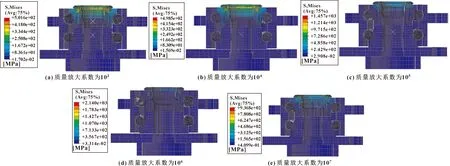
图8 不同质量放大系数下的应力云图

对小内圈的轴向受载情况进行分析，结果如图9所示。其中，小内圈与翻边的轴向接触力和大小内圈挤压变形后内壁的轴向接触载荷之和应该约等于小内圈与第一排滚珠的轴向接触合力和大小内圈阶梯处的轴向合力之和，如图10所示。可知：小内圈内壁由于小内圈膨胀后倾斜度较小，其轴向分量极小；与第一排滚珠的轴向接触载荷随着质量放大系数的增大而增大，这可能是由于滚珠的自由度没有受到约束，在质量放大系数增大后，惯性增大，故冲击力提高。总体的载荷随着质量放大系数的增大而减小，但质量放大系数在10和10时，总体载荷相差较小，且轴向卡紧力分别为34 134.1、29 324.7 N，随后载荷减小明显。故主要考虑质量放大系数在低于10时的分析结果较合理。

图9 小内圈轴向受力分析示意

图10 不同质量放大系数下小内圈的轴向载荷

2.6 模型结果分析和讨论

质量放大系数对旋压铆合工艺仿真存在影响。从仿真耗时上看，仿真时长随着质量放大系数增大而降低。

从仿真提取的各数据对比看，在质量放大系数为10和10情况下，小内圈外径膨胀量均在实测值最大值和最小值之间，且小内圈的受载情况和整体模型的应力分布基本相同。但是，针对翻边外径时，仅质量放大系数为10时在公差的上下极限偏差范围内。在铆装力对比时，各质量放大系数所得结果的趋势和大小均相近。

综上所述，质量放大系数过大会由于惯性过大等问题导致结果不合理。根据对比分析结果，旋压铆合工艺有限元仿真时可以考虑取质量放大系数为10。此外，对于三代轮毂轴承旋压铆合仿真，翻边部位的网格密度同样影响求解结果。当翻边部位网格加密后，可考虑利用10的质量放大系数以提高计算速度，可以尝试将它用于初步分析，为后续更精确的旋铆仿真分析提供参考。

3 结论

(1) 三代轮毂轴承单元的旋压铆合工艺有限元仿真计算量极大、计算耗时长，可考虑利用质量放大系数提高计算速度。

(2) 通过对比分析，发现质量放大系数为10时，仿真结果所受的影响较小；在进行初步分析时，可以考虑取质量放大系数为10，以减少仿真时间，但后续应进一步进行更精确的三代轮毂轴承旋压铆合仿真。

(3) 在回退和静置时间大概约为0.3 s时，小内圈的轴向位移量趋于稳定，铆装力为0 N。后续分析时，可以考虑将回退和静置的时间缩短，以减少仿真时间。