3-PRS & 3P混联机构运动学分析

全红鹏，林光春，黄金月，梁建波，王韬略，廖勋宝

(1.四川大学机械工程学院，四川成都 610065；2.四川阿斯特医疗器械有限公司技术部，四川泸州646100)

0 前言

混联机构兼具串联机构和并联机构的优点，具有承载能力强、刚度好、精度高、响应快、工作范围大等优点，已被广泛用于航天、医疗、工业、军事等各个领域，具有良好的实用性能。

为了更好地运用混联机构，国内外许多学者对其进行了研究。黄俊杰等提出用D-H法和图形可视化相结合的方法对3-PRS并联机构进行正向运动学求解。史晓娟和王高洋将仿真逆解曲线以样条驱动函数形式输入给3-UPU并联机构,得出样条驱动函数下的位置正解曲线。张伟中等设计了一种新型四自由度并联机构，并采用螺旋理论分析了机构的运动特性。崔马茹等采用空间封闭矢量法求解3-URPR并联机构的位置逆解。康件丽等充分利用蒙特卡洛方法的随机性，可以找到3-PRS并联机构的所有位置正解。黄思等人采用双参数数值延拓同伦算法求出正运动学的数值解。黄俊杰和赵俊伟运用遗传算法并结合运动方程给出并联机构运动学位置正解适应度函数和目标函数，将计算结果代入运动方程求出杆长。黄亮等人针对一种3SPS-3SRR并联机构,运用符号法对该机构进行位置分析。杨应洪和尹显明通过支链变异法,提出一种可满足机床2R1T运动要求的2RPS-RPU并联机构，并对其进行了运动学分析。

本文作者提出了一种新型3-PRS & 3P混联机构，对混联机构进行自由度分析；然后对该混联机构进行机构运动学逆解和正解分析，再通过数值算例进行验证；最后讨论了该混联机构动平台2的运动范围。通过以上分析，可以为后面分析该混联机构的动力学及其运动控制提供了一定的理论基础。

1 机构描述以及动、静坐标系的建立

3-PRS & 3P混联机构主要由定平台、动平台1、动平台2、滑块1、滑块2、滑块3、支链1、支链2、支链3、支链4、支链5、支链6组成，如图1所示。其中定平台与动平台1通过3个移动副连接，动平台1与3个滑块通过3个移动副连接，滑块1、滑块2、滑块3分别与支链4、支链5、支链6通过3个转动副连接，支链4、支链5、支链6与动平台2通过3个球副连接。各铰接点分别为：(=1,2,3)、(=1,2,3)、(=1,2,3) 、(=1,2,3) ，如图1所示。且、、构成一个边长为的正三角形；、、构成一个边长为的正三角形；、、构成一个边长为的正三角形；、、构成一个边长为的正三角形。

图1 3-PRS & 3P混联机构构型

为3-PRS & 3P混联机构建立动、静坐标系，如图2所示，其中定平台坐标系为-，动平台1的坐标系为′-′′′，动平台2的坐标系为″-″″″。(=1,2,3)在定坐标系下的方向高度为，(=1,2,3)在定坐标系下的方向高度为，(=1,2,3)在定坐标系下的方向高度为。

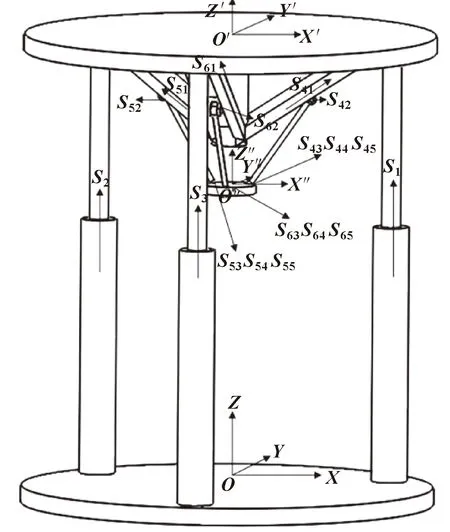
图2 动、静坐标系的建立

各铰接点在定平台坐标系-(初始位型)的坐标为

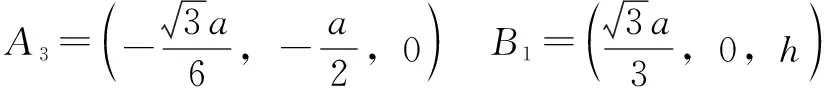
2 机构自由度分析

如图2所示，各支链的运动螺旋系均在定平台坐标系-下表示。支链1的运动螺旋系为

=(0 0 0; 0 0 1)

(1)

对支链1求反螺旋，得到支链1的约束螺旋系为

(2)

对式(2)求二次反螺旋得

(3)

同理支链2和支链3的运动螺旋系与支链1的运动螺旋系是一样的，所以支链2和支链3的约束螺旋系与支链1的也一样。所以动平台1受到5个约束，分别约束绕着轴、轴、轴的转动和沿着轴和轴的移动。所以动平台1只有一个沿着轴的移动自由度。

支链4的运动螺旋系为

(4)

式中:、、、为非零的有限实数。对支链4求反螺旋，得到支链4的约束螺旋为

(5)

式(5)表示过点且平行支链4转动副轴线的约束力。

由于机构具有对称性，同理得支链5的约束反螺旋为

(6)

式(6)表示过点且平行支链5转动副轴线的约束力。

同理支链6的约束反螺旋为

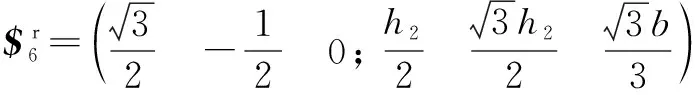
(7)

式(7)表示过点且平行支链6转动副轴线的约束力。

对式(5)(6)(7)求二次反螺旋得：

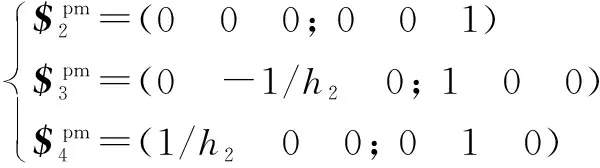
(8)

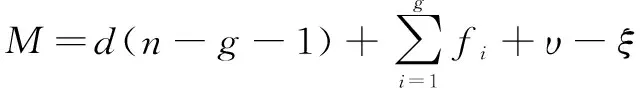
(9)

其中:表示机构的自由度;表示机构的阶数，它依赖于公共约束，=6-;表示机构的构件数(包括固定构件);表示运动副数目;表示第个运动副的自由度;表示冗余约束;表示局部自由度。在该混联机构中=6、=9，运动副所含有的自由度为18(3+3+3+2×3)，冗余约束=10，局部自由度=0。所以机构的自由度为：=6(9-12-1)+18+10-0=4。这与螺旋理论算出来的自由度一致。

3 机构运动学分析

由于支链1、支链2、支链3只改变动平台1的工作空间，因此这里运动学分析时，先假设它们固定不动，而只考虑支链4、支链5、支链6运动的情况，这样就简化了分析的难度，相当于分析3-PRS并联机构。后文再说明考虑了支链1、支链2、支链3运动时的情况。

3.1 机构的逆解分析

混联机构逆解分析就是已知动平台2中心″的位姿，求驱动杆长()(=1,2,3)的输入量。设为球副所在平面的中心，绕着轴的转角为，绕着轴的转角为。

设动平台2中心″在定平台上的坐标=(,,)，(=1,2,3)在动平台2的动坐标系下的坐标为(″,″,″)，则在定坐标系下的坐标表达式为·+(=1,2,3)。其中：

(10)

图3 逆解分析模型

(11)

(=1,2,3)有两组解，为了提高混联机构的刚度，统一取负号，即点从顶部向底部滑动。

3.2 机构的正解分析

已知输入杆长(=1,2,3)，求动平台2的位姿。求解混联机构的正解是有一定难度，而一般构型采用数值分析法进行求解。本文作者也采用数值分析法求解。已知移动驱动杆长的变化规律，则可以求出点的具体数值。点坐标表达式为:·+(=1,2,3)，这样点坐标就含有未知参数、和。由于||=(=1,2,3)，则有

(12)

对式(12)，采用牛顿迭代法来求解该非线性方程组。其中，式(12)可以写成

()=0，=(,,)，=(,,)。根据牛顿迭代法有：+1=-·，其中为雅可比矩阵：

给定输入参数1、2、3，根据给定的初始向量进行迭代，最后得到符合精度要求的向量，即混联机构输出位姿参数。初始向量的给定要符合机构的近似解，不然在一定的精度要求下，可能得不到解。

4 数值实例验证及其仿真

下面通过表1所示的混联机构具体的结构参数，对机构运动学的逆解模型和正解模型进行仿真和验证。

表1 具体的结构参数

其中:表示、、形成的正三角形边长;表示动平台2三个球副中心点形成的正三角形边长;表示点(=1,2,3)到点(=1,2,3)的固定距离;表示点在定坐标系下的初始高度；表示点在定坐标系下的初始高度。

4.1 反解模型

给定动平台2中心点″的运动规律如下：

(13)

在SolidWorks中建立混联机构三维模型，然后将其导入ADAMS中，如图4所示，并将给定的运动规律添加到动平台2中心点。其中在ADAMS中，添加的驱动为一般点驱动。

图4 ADAMS虚拟样机模型

逆解模型的仿真结果如图5(a)所示。根据式(11)，利用MATLAB编程，并绘制出(=1,2,3)杆长变化曲线，如图5(b)所示。

图5 反解模型计算和仿真结果对比

从图5(a)和图5(b)可以看出:两者(=1,2,3)变化曲线高度吻合，从而验证了运动学反解模型的正确性。

4.2 正解模型

给定3个滑块移动驱动运动规律如下：

(14)

在ADAMS中，给定3个滑块的移动驱动，然后仿真求解动平台2的位姿如图6(a)、图6(b)所示。根据式(12)，采用牛顿迭代法，在MATLAB中编程。其中，给定的初始值为(0 0 177.8),求解精度为1×10。绘制动平台2位姿曲线如图6(c)、图6(d)所示。

图6 正解模型计算和仿真结果对比

从图6(a)和图6(c)可以看出:两者动平台2中心点的位置变化曲线高度吻合；从图6(b)和图6(d)可以看出:两者旋转角度、变化曲线高度吻合，从而验证了运动学正解模型的正确性。

5 混联机构动平台2运动范围分析

前面运动学分析都是基于支链1、支链2、支链3杆长保持固定不变，这样做的目的是便于分析该混联机构的正解、逆解。但是，为了增加动平台2的运动范围，可以让一个电机同时驱动支链1、支链2、支链3到达一定的高度保持不变，然后在这一高度下，再次进行混联机构的正解和逆解的分析，分析方式和前面一致，只是竖直方向的位移发生了变化而已。理论上，当只有支链1、支链2、支链3驱动，则该混联机构动平台2中心点″竖直方向的位移可在71.57～221.57 mm内变化。而前面的运动学分析，是动平台2中心点″在定坐标系下，方向为177.80 mm(初始位型)下的正解、逆解而已。

当仍采用式(14)运动规律时，动平台2运动范围如图7所示。可以看出：该混联机构的动平台2具有较大的运动范围，使该混联机构得到了最大化利用。

图7 动平台2运动范围

6 结论

(2)通过余弦定理、空间坐标变换法和牛顿迭代法等建立该混联机构运动学分析的逆解模型和正解模型，并在SolidWorks中建立该混联机构三维模型，再将其导入ADAMS中进行仿真验证。验证结果高度吻合，证明了混联机构逆解模型和正解模型的正确性。

(3)提出了一种3-PRS & 3P混联机构，并对其动平台2的运动范围进行了分析，分析结果表明：该混联机构动平台2具有较大的运动范围。