方钢管柱-H型钢梁单向螺栓平齐式端板连接节点性能研究

刘 伟 徐季漩

(合肥学院 城市建设与交通学院，安徽 合肥 230601)

引言

单向螺栓可以很好地解决装配式钢结构中闭口截面节点安装问题，既可以在不损坏节点其他部位的前提下连接梁柱，又可以尽可能地减少焊接量.近年来国内外很多学者对单向螺栓做了大量的研究，李国强等[1]基于Hollo-Bolt螺栓基础之上研制出国产自锁式8.8级单向螺栓，并对该型螺栓的力学性能做了相关试验.郏书朔等[2]对单边螺栓进行了试验和有限元分析，得到了节点的滞回曲线，对比了单边螺栓和常规螺栓连接节点抗震性能的差异性.蒋蕴涵等[3]针对8.8级国产单向螺栓连接轴向拉伸刚度较小的问题进行了改进.简小刚等[4]学者研究发现Hollo-Bolt的外套管材料比较弱，最后提出优化方案.王静峰等[5]为探究单边高强螺栓端板连接钢管混凝土框架结构在地震作用下的抗震性能，对不同截面形式的钢管混凝土框架试件进行了拟静力试验.这些工作主要集中在试验，通过试验来获得单向螺栓连接节点的一系列力学性能指标，而没有给出节点有关初始转动刚度、极限弯矩、形状系数n的近似公式，本文基于三参数模型，用拟合出的三个近似计算公式描绘出单向螺栓平齐式端板连接的弯矩-转角曲线，并与有限元模型初始刚度、极限弯矩结果对比，验证了近似计算公式的正确性.

1 有限元模型验证

1.1 试验参数

为验证有限元模型的准确性，本文选取同济大学李国强教授[6]的试验模型，选取其中一组试件来进行有限元模型验证.本组试验的主要目的是为了研究螺栓直径对单向螺栓平齐式端板连接的初始刚度和极限弯矩的影响.试件为矩形钢管柱-H型钢梁，矩形钢管柱高1.2 m，H型梁长1 m，螺栓选用同济大学研究发明的单向螺栓STUCK-BOM，梁、柱、端板截面尺寸见表1，节点详图如图1所示.正式加载时，梁端由作动器施加单向静力荷载.

表1 试件参数表 mm

图1 试件节点详图(单位：mm)

1.2 有限元模型

为了与试验结果尽可能相近，有限元模型中的材料属性参考材性试验，节点试件材料特性[7]如表2所示.为了得到梁端极限位移，在梁端腹板中心处设置一个集合.节点中的部件全都选用C3D8R单元.加密区网格尺寸为10 mm,非加密区网格尺寸为40 mm，螺栓网格尺寸为4 mm，节点网络划分情况如图2所示.模型分为三个分析步，初始分析步对柱端施加完全固定约束，第一个分析步对螺栓施加70 kN预紧力，第二个分析步使螺栓固定在当前长度，第三个分析步为在梁端施加竖向荷载.

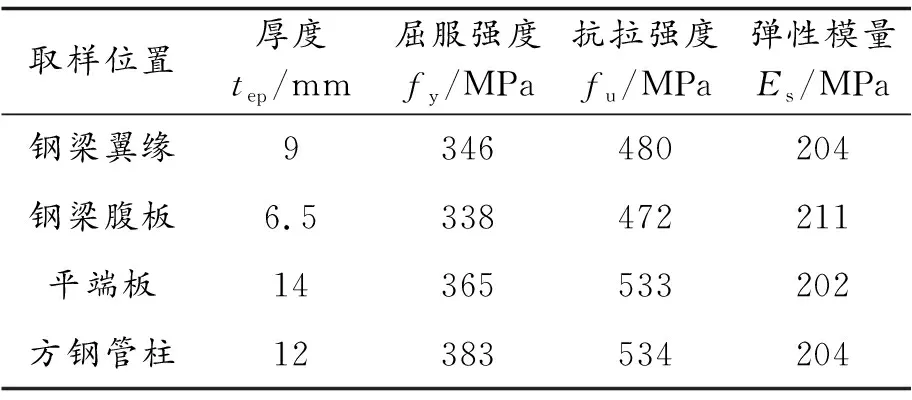
表2 钢材材性试验结果

图2 节点及螺栓网格划分

1.3 有限元结果

随着梁端荷载逐渐增大，外套管分支与螺栓孔相互挤压，使得外套管分支向内收缩，螺栓产生滑移.端板与柱壁间的缝隙不断增大，柱上排螺栓孔周围产生鼓曲变形，随着梁端荷载逐渐增加，最上排螺栓几乎被拔出，导致节点丧失承载力.

模型破坏应力云图如图3所示，外套管分肢在梁端荷载作用下与柱螺栓孔挤压造成应力集中，柱壁发生鼓曲变形且在柱最上排螺栓孔周围产生应力集中.从图3可以看出，螺栓杆和外套管达到了极限承载力.节点极限承载力为128 kN，梁端极限位移为136 mm.

图3 节点及螺栓破坏应力云图

1.4 对比分析

表3给出了节点有限元模型与节点试验得到的初始转动刚度与极限弯矩[6-8].试件SR1-1弯矩-转角曲线如图4所示，当梁端转角达到0.175 rad时，节点发生破坏，ABAQUS只显示极限承载力而不能显示螺栓破坏后节点承载力急剧减小的现象[9]，因此只需比较节点转角达到0.175 rad之前有限元模型弯矩转角曲线与节点试验弯矩转角曲线.通过对比看出，有限元模型的结果与试验数据非常接近，表明有限元模型具有一定的准确性和可靠性.

表3 计算结果对比

图4 试件SR1-1弯矩-转角曲线

2 有限元模型参数分析

2.1 初始刚度

为探索影响节点初始刚度和极限弯矩的主要参数，利用ABAQUS建立了22个单向螺栓平齐式端板连接有限元模型.表4列出了模型1～22的截面尺寸，具体参数含义如图5所示.

表4 有限元模型主要参数 mm

续表4

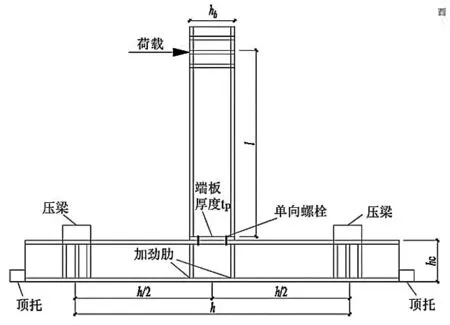
图5 有限元模型详图

通过对以上22个模型进行有限元分析，得到有限元模型的初始刚度以及极限弯矩，几乎所有模型都是螺栓破坏，模型的初始转动刚度和极限弯矩数值见表5.

表5 节点初始转动刚度和极限弯矩

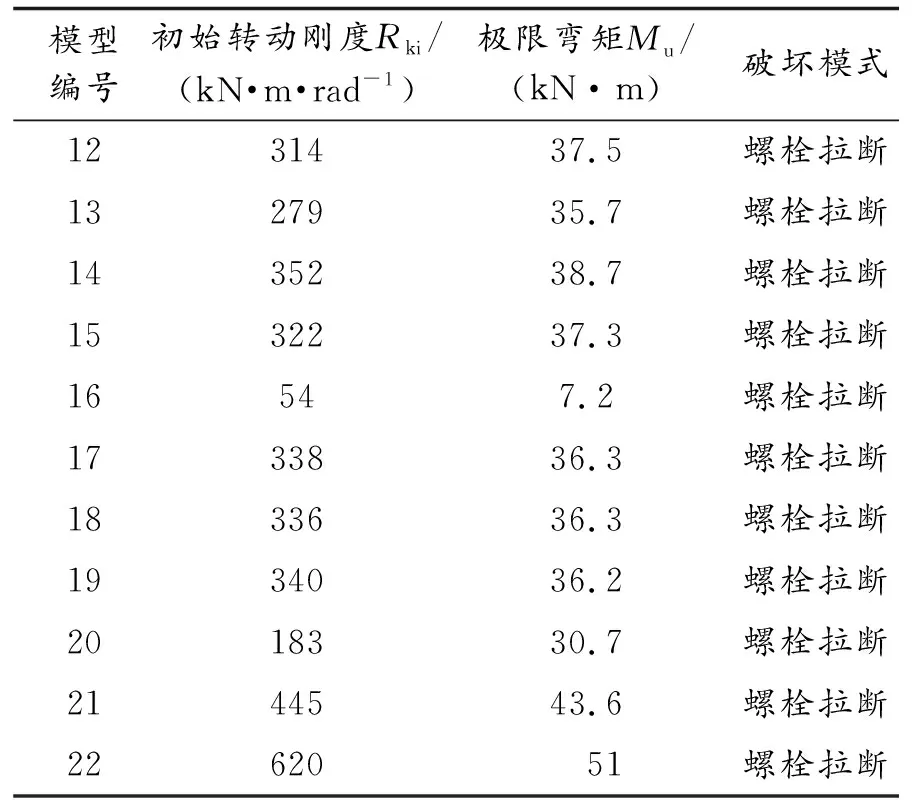
续表5

随着参数的改变，单向螺栓平齐式端板连接初始刚度值的变化规律以及影响程度如图6～图12所示.

图6 柱壁厚度对初始刚度的影响

从图6-图12可以看出，对单向螺栓平齐式端板连接节点初始转动刚度影响较大的参数有：柱壁厚度tc、梁高度hb、螺栓直径d、螺栓端距p2、螺栓边距p3.当柱壁厚度从10 mm增大到16 mm，节点初始刚度提高25%；当螺栓边距从50 mm增加到80 mm，节点初始刚度减小84%；当螺栓端距从25 mm增加到45 mm，节点初始刚度减小20%；当梁的高度从200 mm增加到350 mm，节点初始刚度提高70%.其中节点初始转动刚度值随着柱壁厚度、梁高度的增加而变大，随着螺栓端距p2以及螺栓边距p3的增大而减小.在现场施工过程中，螺栓端距p2至少要大于2d0，螺栓中心至构件边缘距离p3不能大于4d0.d0为螺栓孔孔径.保留对初始刚度影响较大的因素，拟合出初始转动刚度的近似公式，见式(1).

(1)

式中：Rki为初始刚度；E为钢材的弹性模量；hb为梁的高度；tc为柱壁厚度；d为螺杆直径，d0为螺栓孔孔径.

用式(1)重新计算初始转动刚度，计算结果及与有限元解的误差见表6.

实际工程中，螺栓中心至构件边缘距离p3不能大于4d0，而模型16螺栓边距过大，不符合实际工程要求，因此忽略模型16的计算结果.如表6所示，两者误差基本控制在10%以内.

2.2 极限弯矩

通过表5可知，对极限弯矩值影响大的参数有柱壁厚度tc、螺栓边距p3、梁的高度hb.当柱壁厚度从10 mm增大到16 mm，极限弯矩提高32%；当螺栓边距从50 mm增加到80 mm，极限弯矩减小81%；当梁的高度从200 mm增加到350 mm，极限弯矩提高39.8%.保留对极限弯矩影响大的参数，略去对极限弯矩影响小的参数，通过数值拟合出极限弯矩的近似计算公式，见式(2).

(2)

式中：Mu为极限弯矩；E为钢材的弹性模量；bb为梁的宽度，hb为梁的高度；tc为柱壁厚度；d为螺杆直径，d0为螺栓孔孔径.

用式(2)重新计算极限弯矩，计算结果及与有限元解的误差见表7.

实际工程中，螺栓中心至构件边缘距离p3不能大于4d0，而模型16螺栓边距过大，不符合实际工程要求，因此忽略模型16的计算结果.如表7所示，两者误差基本控制在10%以内.

2.3 形状系数

本文采用三参数模型来拟合单向螺栓平齐式端板连接节点的弯矩-转角曲线.其形式为：

式中，θ—梁端转角;M—节点转角弯矩;Rki—初始转动刚度;n—形状系数；θ0—参考塑性转角，θ0=Mu/Rki;Mu—极限弯矩.

在实际工程中，无法对每种单向螺栓平齐式端板连接进行试验以获得形状系数n[10].因此，需要我们通过参数化分析，拟合出形状系数n的近似求解公式.形状系数n的拟合值及近似值见表8.本节以表4中的有限元模型为研究对象，将22个有限元模型的初始刚度、极限弯矩代入三参数模型公式中，求得形状系数n的值，使

通过对22个有限元模型进行分析，发现形状系数n与θ0有关，将参考塑性角θ0的值作为x轴，形状系数n的值作为y轴，如图13所示，形状系数n随参考塑性角θ0呈线性分布.为了能快速得到形状系数n的值，利用最小二乘法，得到形状系数n的近似求解公式，见式(3).

n<0.11n=267.63θ0-10.35

0.11≤n<0.13n=172.647θ0-8.2

(3)

n≥0.13n=335.55θ0-39.16

3 基于三参数模型的M-θ曲线研究

利用本文所得到的三个公式，得到节点初始刚度、极限弯矩、形状系数，代入三参数模型中，绘制出三参数模型M-θ曲线.由于篇幅限制，每种参数变换给出一个模型的M-θ曲线，通过图14-图21可以看出基于三参数模型的M-θ曲线与通过有限元模型的M-θ吻合地较好，从而验证了三参数模型的正确性.

4 结论

在试验现象和试验数据吻合的有限元模型基础之上，通过对单向螺栓平齐式端板梁柱连接节点有限元模型的初始刚度、极限弯矩进行研究分析，可以得出以下结论：

(1)本文所建立的有限元模型与参考文献[6]中试验数据吻合良好，表明所建立的有限元模型具有一定的准确性和可靠性.

(2)通过参数化分析得知，对节点初始刚度和极限弯矩影响较大的因素依次是梁高度hb、螺栓边距p3、柱壁厚度tc.当柱壁厚度从10 mm增大到16 mm，节点初始刚度提高25%；当螺栓边距从50 mm增加到80 mm，节点初始刚度减小84%；当螺栓端距从25 mm增加到45 mm，节点初始刚度减小20%；当梁的高度从200 mm增加到350 mm，节点初始刚度提高70%.对极限弯矩值影响大的参数有柱壁厚度tc、螺栓边距p3、梁的高度hb. 当柱壁厚度从10 mm增大到16 mm， 极限弯矩提高32%；当螺栓边距从50 mm增加到80 mm，极限弯矩减小81%；当梁的高度从200 mm增加到350 mm，极限弯矩提高39.8%.

(3)通过对22个单向螺栓平齐式端板连接有限元模型分析，保留对初始转动刚度、极限弯矩影响大的参数，略去对初始转动刚度、极限弯矩影响小的参数，拟合出初始转动刚度、极限弯矩计算公式.结果表明：拟合公式计算结果与有限元解误差基本在10%以内.

(4)利用最小二乘法，拟合出形状系数的近似公式，绘制出三参数模型的M-θ曲线，结果显示三参数模型的M-θ曲线与有限元模型的M-θ吻合得较好，从而验证了三参数模型的正确性.