也谈数学归纳法在解题中的应用
内蒙古巴彦淖尔市临河区第一中学
薛思谦
1 引言
对于一类与正整数有关的命题的论证问题,当其他方法无法证明时,往往想到数学归纳法.用数学归纳法证明问题分三个步骤:第一步先证明当n取初始值n0(n0∈N*)时命题成立.这是第二步的前提,不可省去,初始值n0视题目而定,不一定是1.第二步先假设当n=k(k∈N*,k≥n0)时命题成立,在此基础上,推证当n=k+1时命题也成立.这一步骤是数学归纳法最关键的步骤,要求对有关表达式进行恰当变形,而且在证明当n=k+1时命题成立时,必须以“当n=k时命题成立”为条件,否则是“假数学归纳”.第三步则由以上两个步骤得出所证结论.这一步必须规范书写,否则就不是数学归纳法.由此可见,数学归纳法不同于其他数学方法,它是一个特别注重书写格式和过程规范的证明方法,这一点要引起大家的注意.在数学解题中,数学归纳法有着广泛的应用.主要体现在以下四个方面:用数学归纳法证明等式;用数学归纳法证明不等式;用数学归纳法证明数的整除性;用数学归纳法证明猜想的结论.下文举例说明.
2 用数学归纳法证明等式
对于有些与正自然数有关的等式的证明问题,当其他证明方法无能为力或过程太繁琐冗长时,就可以采用数学归纳法.

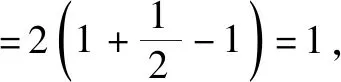
(2)假设n=k(k≥2,k∈N*)时,等式成立,即f(1)+f(2)+f(3)+……+f(k-1)=k[f(k)-1],上式两边同时加上f(k),得
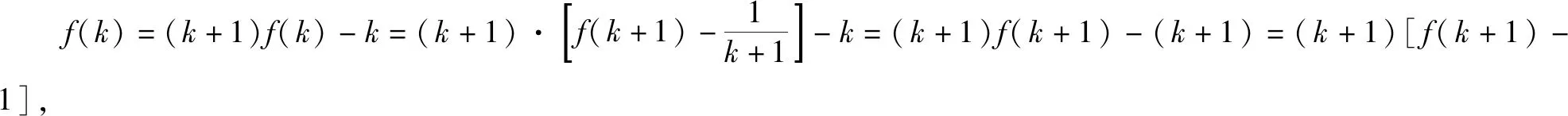
即当n=k+1时等式依旧成立.
由(1)(2)可知,f(1)+f(2)+f(3)+……+f(n-1)=n[f(n)-1]对n≥2,n∈N*都成立.
点评:用数学归纳法证明等式问题的关键点在于弄清所证等式两边各项的规律,等式两边含有的项数,初始值n0是哪个数.由n=k出发证明n=k+1命题也成立时,除了要考虑等式两边变化的项之外,还要充分利用n=k时的式子.
3 用数学归纳法证明不等式
用数学归纳法证明与n有关的不等式,通常出现两种情况:一是直接给出不等式,按要求进行证明;二是给出两个式子,按要求比较它们的大小.对第二类问题可先对变量n取最初几个特殊值分别验证比较,从而得出所证结论,最后再用数学归纳法证明这个不等式.
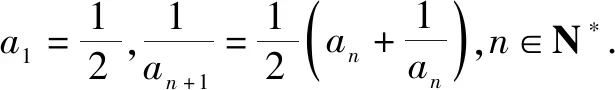
(1)证明:0 证明:(1)①当n=1时显然成立; 综合①②可知,0 点评:本题第(1)问用了数学归纳法,第(2)问用的是综合法,请注意它们之间的区别.用数学归纳法证明不等式的关键还是由n=k成立,推证n=k+1时也成立,用了归纳假设后,可采用其他证明不等式的所有方法,如分析法与综合法、比较法与放缩法等. 关于与正整数n有关的指数型代数式的整除性问题的证明,一般用到两种证明方法:一是直接法,即构造二项式,并利用二项式定理将其展开进行证明;二是利用数学归纳法,严格按照数学归纳法的三个步骤加以论证. 例3试证(3n+1)·7n-1(n∈N*)能被9整除. 证明:(1)当n=1时,(3+1)×7-1=27能被9整除,故命题成立; (2)假设当n=k时命题成立,即(3k+1)·7k-1(n∈N*)能被9整除,那么 [3(k+1)+1]·7k+1-1 =(3k+1)·7k+1+3·7k+1-1 =7·(3k+1)·7k+3·7k+1-1 =(3k+1)·7k-1+6·(3k+1)·7k+3·7k+1 =[(3k+1)·7k-1]+(18k+27)·7k, 由归纳假设(3k+1)·7k-1(n∈N*)能被9整除及(18k+27)·7k是9的倍数,可得[(3k+1)·7k-1]+(18k+27)·7k能被9整除,即n=k+1时,命题成立. 由(1)(2)可知,命题对任意的n∈N*都成立. 点评:用数学归纳法证明整除性问题,关键还是在第二步,将[3(k+1)+1]·7k+1-1变形成[(3k+1)·7k-1]+(18k+27)·7k,考查等式的变形能力. 先归纳,再猜想,后证明,是一种不完全归纳法与数学归纳法“联合作战”的解题模式. (1)求f1(x),f2(x);(2)猜想fn(x)的表达式,并证明你的结论. 证明:①当n=1时,由(1)知猜想的结论正确; ②假设当n=k,k∈N*时,结论正确,即有 =(-1)k-1·ak-1·(bc-ad)·k!.[(ax+b)-(k+1)]′ 即当n=k+1时结论成立. 由①②可知,对一切n∈N*猜想的结论正确. 点评:本题的第(1)问,借助题设条件运用导数知识直接求解;第(2)问归纳法推证时,能借助(1)猜想结论,进而运用数学归纳法分析推证,从而获证.本题证明的难点有两个:一是猜想的结论不可有丝毫差错,二是从n=k,k∈N*到n=k+1中的式子的变形. 本文最后值得一提的是,数学归纳法作为一种数学证明的方法,虽然用途比较广泛,尤其是在高考压轴题或数学竞赛中,有着不可或缺的作用,但由于它的书写格式要求比较高,所以建议慎用.当采用别的证法也能顺利解决问题时,还是以其他证明方法为上策.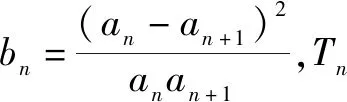
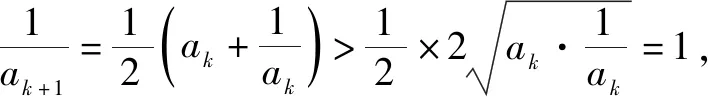
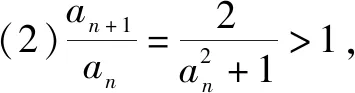
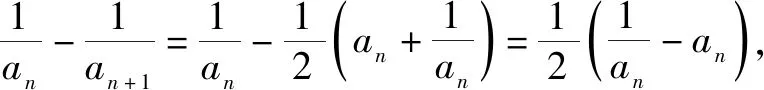
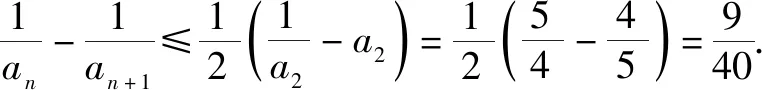
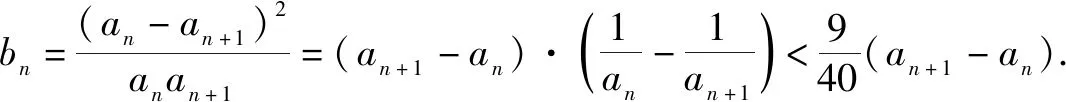
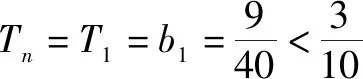
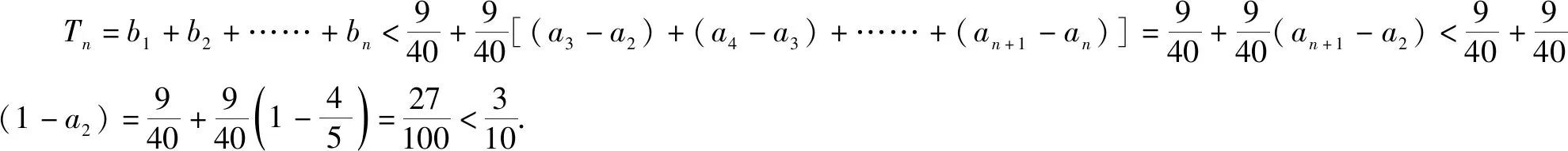
4 用数学归纳法证明整除性问题
5 用数学归纳法证明猜想的结论
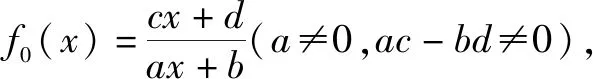
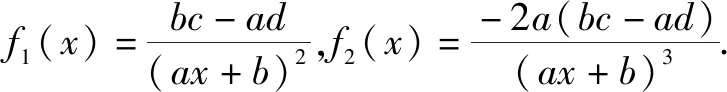
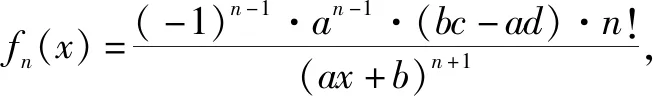
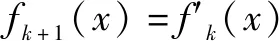
6 结语

