水陆两栖六足机器人的设计与性能评估
王 宇 周 爽 李亚鑫
西南石油大学电气信息学院,成都,610500
0 引言
与单一环境下活动的水下机器人或足类机器人不同,两栖机器人通常搭载具有独特机械设计与运动特性的复合推进机构,以保障它可在陆地、水下以及水陆交接的过渡环境中执行包括生态环境监测、水下资源勘探、灾后搜索救援在内的众多任务[1-3]。
水陆两栖机器人应用前景广阔,众多学者受两栖动物外形结构、生理特征、运动规律的启发,提出了一系列仿生机器人样机。哈尔滨工程大学王立权教授团队研发的足桨混合驱动水陆两栖机器人就是以海蟹为仿生原型设计而成的[4-5],根据任务所在的不同环境,机器人可灵活选取步行足或游泳桨作为运动驱动方式,但由于该机器人推进装置完全模仿海蟹的运动生理特征,因此需要具备水下推进和陆地爬行两套不同执行机构。中国科学技术大学张世武教授团队提出的AmphiHex则基于部分仿生的设计思想[6-8],陆地环境以蟑螂为仿生目标采用可变形弧形腿的推进机构,在水下借鉴鱼类波动运动特征,采用波动矢量推进方式,因此,针对AmphiHex水陆两栖机器人设计而成的可变性腿-鳍复合推进方式仅采用一套变形机构即可实现运动腿形状的有效改变,从而为水下、陆地两种复合运动提供了解决方案。中科院自动化研究所提出了轮-桨-鳍多模态仿生两栖机器人[9-10],在水下可结合仿鱼推进和仿海豚式游动,在陆地则驱动机器人身体两侧的轮式运动机构。考虑到两栖机器人需要应对不平坦的水陆环境,相较于轮式运动方式,采用步行足的腿式两栖机器人具有更好的地形适应能力。因此,日本国立香川大学的郭书祥教授团队为四足球型两栖机器人提出了腿式运动肢-复合喷水电机的一体化设计[11-13],一方面该机器人可采用腿式结构在陆地上实现较丰富的步态控制;另一方面由于每一条运动肢在水下都是矢量推进器,因此通过合理配置四足的相对位置,球形机器人可在水下轻松地完成包括直行、旋转、上浮和下潜在内的多自由度运动。但由于该机器人是四足设计且每条腿只有两个自由度,故大大限制了机器人在运动过程中姿态控制方面的多样性。
综上所述,两栖机器人的设计、推进器的结构、水陆间运动机构的切换方式都决定了机器人对多变环境的适应性及其运动的机动性、灵活性。针对以上挑战,本文提出了一款水陆两栖六足机器人,它搭载的三自由度步行足机构不仅结合了六足昆虫类运动肢的生理特征,还通过复合喷水电机实现了水陆运动切换简单的一体化矢量推进方式。
1 水陆两栖六足机器人设计
1.1 机械设计
本文提出的水陆两栖机器人采用部分仿生的设计思想,其整体机械设计如图1所示。该机器人主要由用于密封控制电路的半球形机舱和均匀分布于机身的6条足式复合运动肢组成。

图1 水陆两栖六足机器人模型图Fig.1 Amphibious hexapod robot model
机器人六足设计的灵感主要源于如蚂蚁、蟑螂等昆虫类突出的陆地运动性能。通过观察它们的生理特征不难发现,每条运动肢分别由基节、股节、胫节和跗节等组成,这种多自由度的腿部结构不仅保证了它们在复杂陆地环境的通过性,更提高了爬行运动的稳定性。因此,本文在综合了六足昆虫类生理特性与机械设计复杂度等因素后,提出了模拟基节-股节-胫节的三自由度运动肢结构。初始状态下每条运动肢呈圆周状均匀分布于机身,这在保证每条运动肢具有足够运动空间的前提下,避免了相邻足间的相互干扰。与此同时,为了实现水陆两栖机器人在水下运动的高灵活性与机动性,受水母、乌贼等喷射推进方式的启发,通过在上述陆地步行足上搭载喷水电机,设计出了综合陆地爬行与水下矢量推进的机器人复合运动肢。该运动肢采用了三连杆并联结构,其基节、股节和胫节关节处的三个防水舵机不仅可以合理控制每条腿在爬行过程中的相对位置,而且由于喷水电机的出水口配置于足端,因此三自由度运动机构可使每条运动肢成为一个独立矢量推进器,方便机器人实现灵活的水下运动。如图1细节图所示,该复合运动肢的基节由于近机身侧,负荷较重,因此由铝合金CNC加工而成以确保其结构强度。相较之下,股节与胫节则采用韧性好、质量小的高性能尼龙3D打印而成(3D打印机型号:HP Jet Fusion 3D 4200)。同时,为了尽量减小机器人爬行过程中每条运动肢舵机上承受的负荷,质量较大的喷水电机被固定于机舱外侧而非运动肢足端。基于以上考量设计而成的水陆足式复合运动肢既保证了两栖机器人在陆地复杂地形的爬行能力,又通过矢量推进方式实现了机器人在水下的灵活运动。
此外,用于密封机器人控制电路并且负责固定运动肢的机舱也由高性能尼龙材料3D打印而成。由该种材料制成的机舱质量小且强度高,这不仅减小了机器人陆地爬行时运动肢的负荷,也确保了其水下运动时机身可承受足够大的压力。
1.2 电气电路设计
为了方便控制两栖机器人在陆地与水下的各种运动姿态,设计了图2所示的密封于机舱内部的机器人电气电路。该机器人主控板采用Arduino Mega 2560,通过舵机控制板(SSC-32)控制6条运动肢上18个舵机转动,从而合理调整每条三自由度复合运动肢的足端位姿。为兼顾机器人水陆两栖的运动环境,舵机使用防水舵机(Hitec HS-5646WP)。机器人通过搭载5300 mA·h的锂电池给主控板和舵机控制板供电。与此同时,为保证机器人在水下具有良好的续航能力,本文采用6个1300 mA·h锂电池分别为各条运动肢上的喷水电机供电,可保证其在额定功率下连续工作1.5 h。机器人在水下矢量推力的大小则由主控板产生的6路脉宽调制(pulse width modulation,PWM)信号控制。PWM信号通过调节喷水电机转速进而改变足端喷水口的流速,达到控制矢量推力大小的目的。此外,为了保证机器人在陆地与水下运动的机动性,还配置了感知自身姿态的陀螺仪(BNO055)与检测水下深度的压力传感器(MS5837-30BA),通过实时获取机器人当前运动状态并反馈给主控板,为水陆两栖机器人更好地适应复杂环境提供了硬件方面的支持。

图2 电气电路设计模块图Fig.2 The framework of electrical circuit
2 运动规划
2.1 陆地运动规划
两栖机器人在陆地爬行时面临众多挑战,特别是应对斜坡地形遇到的机身稳定性问题。本文在陆地运动规划中重点解决机器人适应不同斜坡坡度的运动控制问题。基于运动学分析,本文首先在运动肢的基节、股节、胫节及足端分别建立D-H(Denavit-Hartenberg)坐标系,用以获取运动肢各关节角度与足端位置之间的关系。由于机器人6条运动肢结构相同且呈圆周对称分布,因此任意选出一条运动肢建立D-H坐标系,如图3所示,在此坐标系下运动肢D-H参数如表1所示。其中,αi为连杆转角,ai为连杆长度,di为连杆偏距,θi为关节角。根据坐标系之间的位姿变换关系,可以得到机器人足端坐标系{O3}相对于基节处坐标系{O0}的位姿变换矩阵:

图3 运动肢D-H坐标系Fig.3 The D-H coordinate of one leg
式中,sθ1表示sinθ1;cθ1表示cosθ1;sθ23表示sin(θ2+θ3);cθ23表示cos(θ2+θ3)。
为了提高机器人在斜坡地形下的运动性能,本文借助移动效率高的三足步态,将爬坡角度融入步态规划中并实现了一种可适应于斜坡爬行的三角步态。具体过程如下:机器人可依据陀螺仪检测到的当前位置坡度自适应地调节机身质心与斜坡的垂直高度;与此同时,通过规划三角步态中运动肢足端的轨迹及实时的机身姿态,由逆运动学求解运动肢基节、股节、胫节处关节角θ1、θ2、θ3:
θ1=arctan 2(py,px)
(1)
(2)
(3)
式中,p为足端的位置矢量。
式(1)~(3)即可用来驱动运动肢,进而提高机器人对不同坡度的适应能力。
在爬行过程中,机器人三角步态规划如图4所示,将机器人6条腿分为A、B两组,R2、L1、L3为A组,R1、R3、L2为B组。机器人整个爬行过程分为准备阶段和爬行阶段。由于机器的6条运动肢初始化下呈圆周对称分布,因此在准备阶段A组腿抬起向前摆动一个步长,B组腿支撑不动,为机器人爬行做好准备。在爬行阶段,步态周期设定为T,在0~T/2时间段,B组腿作为摆动相,抬起腿向前摆动一个步长,A组腿作为支撑相,向后摆动一个步长,机身向前移动一个步长;在T/2~T时间段,A组腿作为摆动相,抬起腿向前摆动一个步长,B组腿作为支撑相,向后摆动一个步长,机身再次前进一个步长。因此,在一个完整步态周期下机器人机身可向前前进两个步长,当A、B两组腿连续交替摆动-支撑时,机器人可向前实现三角爬行步态。这种步态在蚂蚁类六足昆虫中比较常见,由于每组运动肢在处于支撑相时可构成三角形支架结构,因此稳定性好,并且两组运动肢交替前进,移动效率较高。
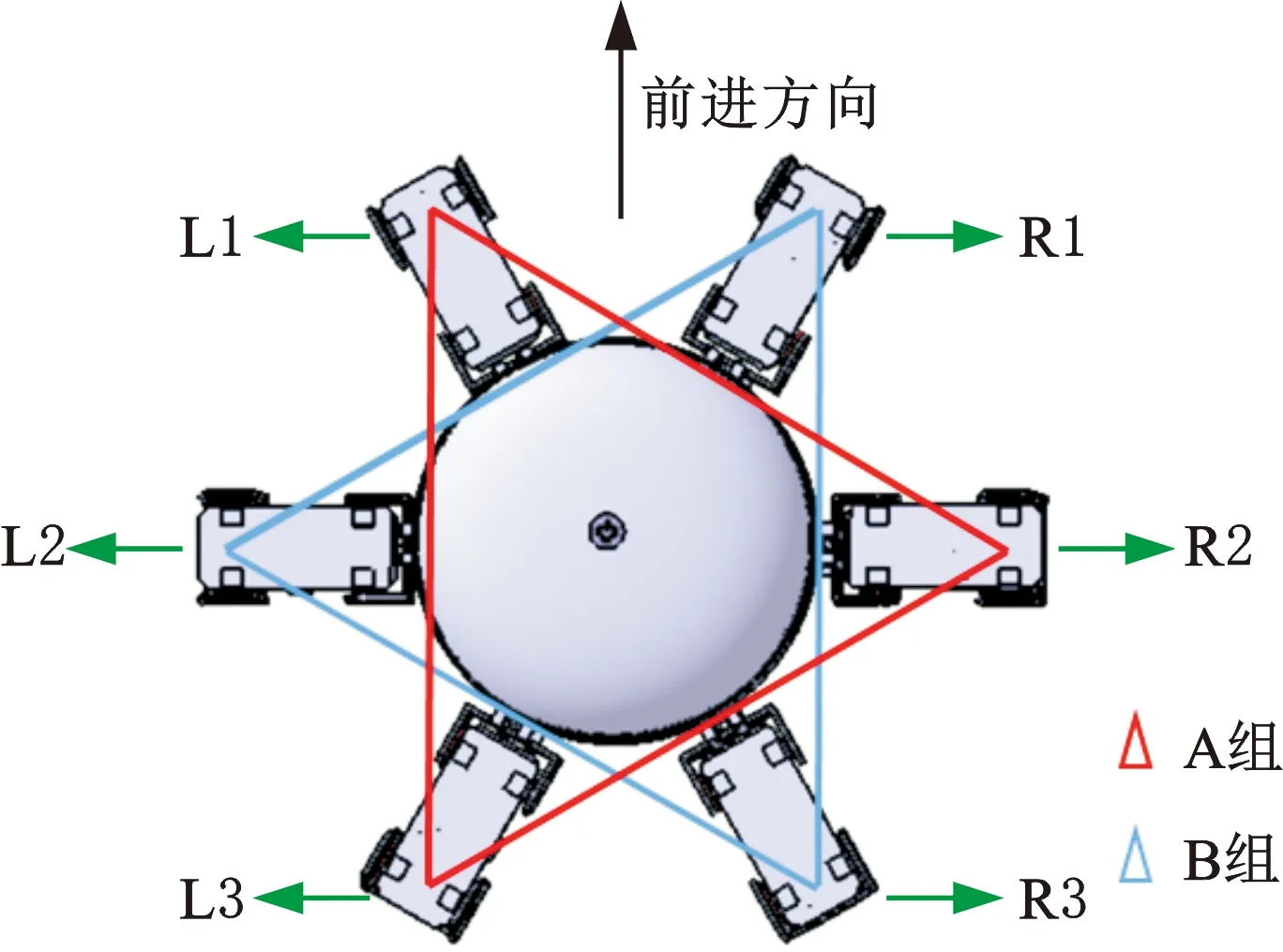
图4 三角步态示意图Fig.4 The tripod gait planning
2.2 水下姿态规划
由于水陆两栖机器人的每条运动肢都是一个复合了喷水电机的三自由度矢量推进器,因此通过合理地改变运动肢的姿态及喷水电机的转速,机器人即可控制矢量推进器的推力方向和大小,从而确保其在水下实现包括直行、旋转、上浮和下潜在内的多自由度运动。
具体来说,当矢量推进器调整为图5a所示的姿态时,机器人可实现直行运动。此时,矢量推进器1、2、3相互平行,推进器4、5与水平方向成60°。机器人若要实现原地旋转,其矢量推进器可配置为图5b所示的姿态,此时6组推进器在机器人质心处产生的转矩将使其逆时针原地旋转,顺时针原地旋转运动同理。当矢量推进器配置成图5c所示的姿态时,6条运动肢足端垂直向下喷水,机器人可实现上浮运动。当矢量推进器调整为图5d所示的姿态时,运动肢足端喷口斜向上45°,且由于矢量推进器均匀分布于机身,机器人在合力作用下实现下潜运动。综上所述,通过合理配置6组矢量推进器的相对位置,两栖机器人在水下可实现灵活的多自由度运动。

(a)直行 (b)旋转

(c)上浮 (d)下潜图5 水下多自由度运动示意图Fig.5 Underwater motion of multi-DoF
3 斜坡爬行ADAMS仿真
为了验证提出的陆地运动规划方法可以协助机器人更好地适应不同斜坡坡度,本文在ADAMS 2019环境下对机器人进行了运动学仿真实验,对比了该机器人在平坦地面、4°斜坡、8°斜坡和12°斜坡下机器人机身的稳定性。
在仿真实验中,首先将两栖六足机器人的三维模型导入ADAMS中,如图6所示,其所有运动肢的18个转动关节设置为旋转副,由于机器人的其他部件不需要移动和转动,因此设置为固定副。本文采用了MATLAB Robotics Toolbox规划运动肢的足端轨迹并求解相应基节、股节、胫节处的关节角。运动肢的轨迹规划分为摆动与支撑两部分,步态周期T设定为2 s,步长为4 cm,最大抬腿高度为4 cm。将MATLAB求解出的逆运动学结果导入ADAMS中生成样条曲线,并作为驱动函数使18个旋转副旋转,进而驱动机器人完成平地、各坡度斜坡的爬行任务。与此同时,为了保障机器人足端与行走地面有足够的摩擦力,在ADAMS中静态摩擦因数和动态摩擦因数分别设置为0.3和0.25,仿真时长为24 s。
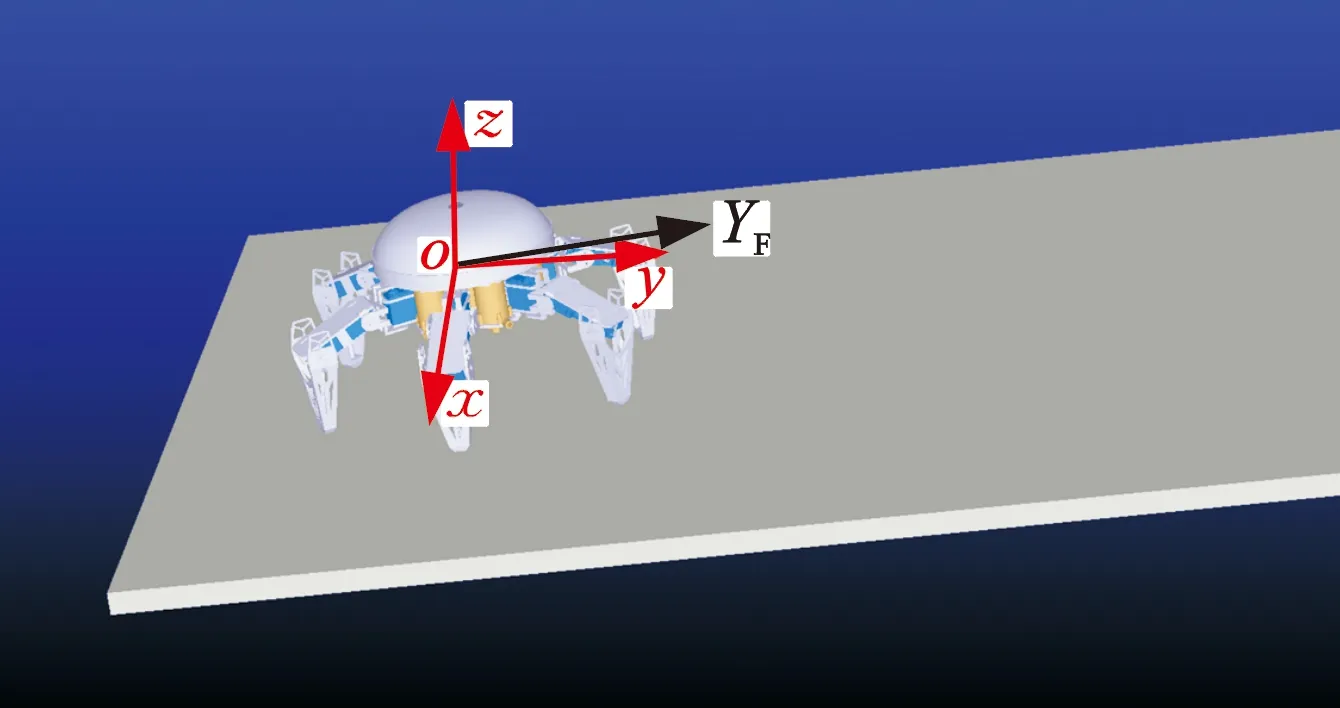
图6 导入ADAMS中的机器人三维模型Fig.6 The imported robot 3D model in ADAMS
为方便观察机器人在运动过程中机身的稳定性,本文在机器人爬行起始位置建立全局坐标系oxyz,如图6所示。机器人在起始位置时的质心刚好位于坐标系原点,oxy平面平行于水平面,z轴正方向垂直于水平面,y轴方向指向机器人在平地爬行时水平前进的方向。YF记为机器人沿斜坡前进时的方向。图7分别展示了机器人在平地、 4°斜坡、8°斜坡和12°斜坡下质心在全局坐标系下位移随时间变化的情况。与平地爬行相比,机器人质心在x轴方向的左右摆动位移基本一致,均不超过0.3 cm。在z轴方向上,机器人机身随坡度虽上下波动略有增加,但总体来说位移曲线平滑没有突变发生,这表明机器人在爬坡过程中机身质心上下波动较小,运动稳定性较高。此外,观察机器人质心在y轴的位移变化情况可知,机器人不论是在平地还是斜坡,其每一个步态周期位移均一致,运动流畅平稳度较好,且运动肢之间也没有相互干扰的情况出现。以上仿真结果一方面表明了机器人在爬行过程中具有较好的稳定性,同时也从侧面验证了该两栖机器人机械设计的合理性。

(a)平坦地面机器人质心轨迹 (b)4°斜坡机器人质心轨迹
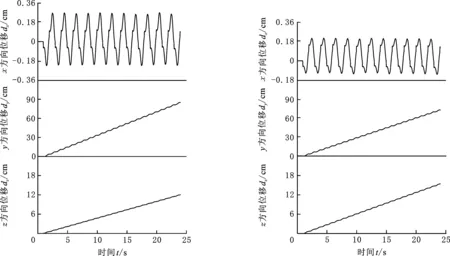
(c)8°斜坡机器人质心轨迹 (d)12°斜坡机器人质心轨迹图7 机器人不同斜坡爬行质心位移曲线Fig.7 Displacement curve of the robot centroid on the different slopes
4 实验
为进一步评估两栖机器人的运动性能,本文搭建完成了图8所示的水陆两栖机器人样机,并分别测试机器人在陆地适应斜坡地形以及在水下实现多自由度运动的各项性能。

图8 水陆两栖六足机器人样机Fig.8 Amphibious hexapod robot prototype
4.1 陆地实验
本实验采用已搭建好的机器人样机在与仿真相同实验地形下(平地、4°斜坡、8°斜坡和12°斜坡)进一步测试陆地运动性能。机器人所爬行的斜坡由一块长1.4 m、宽0.7 m的木板搭建而成,且设置了标尺以方便观测机器人前进的位移情况。图9展示的是机器人在12°斜坡上向前爬行的过程,其中0~6 s为机器人获取斜坡坡度并自适应调节机身质心高度的阶段,6~30 s为机器人爬行阶段。图10展示了机器人在不同斜坡下的运动性能,可以看出,不论平地还是斜坡,爬行位移随时间呈线性增长趋势。这表明机器人爬行过程中速度恒定且运动平稳,对不同坡度的斜坡具有较好的适应性。

图9 机器人在12°斜坡爬行过程Fig.9 The process of the robot crawling on the 12° slope
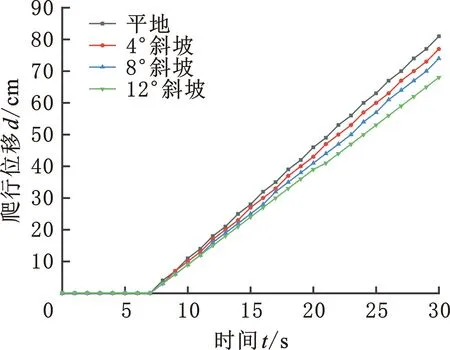
图10 不同斜坡下的运动性能Fig.10 Creeping performance of the robot prototype
表2对比了机器人在仿真环境下和现实环境中的平均速度,总体而言,机器人的运动速度随坡度的增加而减慢。样机在平面爬行时,机器人前进速度高达3.375 cm/s,机器人在12°斜坡爬行时速度减低至2.833 cm/s。在此需要说明,由于机器人足端与斜坡摩擦力有限,本文只验证了机器人在不超过12°斜坡下的运动性能,以防止其在爬行过程中出现下滑现象。

表2 样机的平均速度与仿真结果对比Tab.2 Comparison of creeping speeds between robot prototype and simulation results
4.2 水下实验
为评估两栖机器人样机在矢量推进器驱动下的多自由度运动性能,本文进行了包括直行、旋转、上浮和下潜在内的水下实验。实验均在一个小型户外泳池中进行,其长宽高分别为4 m×1.5 m×1.6 m。
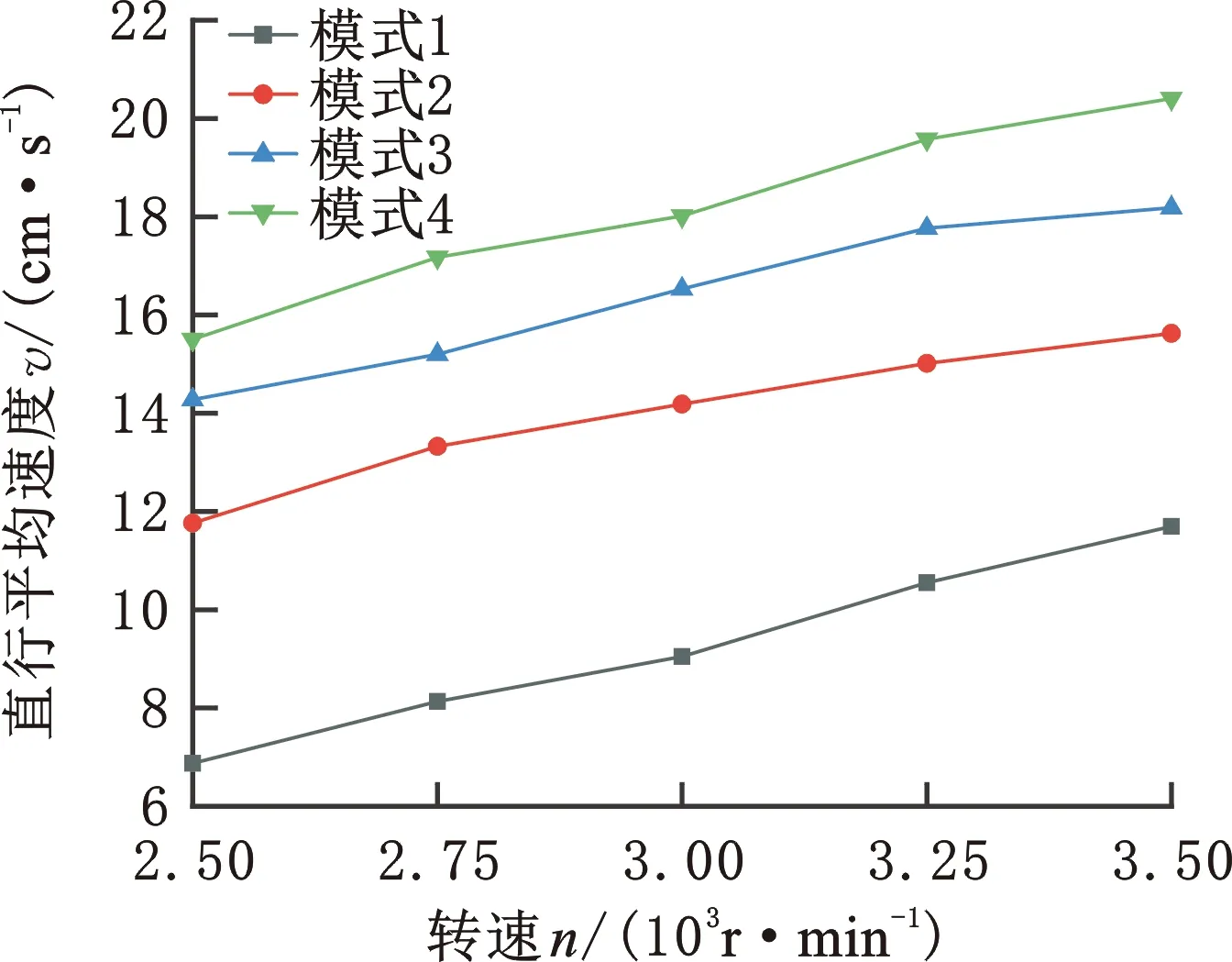
对于水下直行运动,机器人6条运动肢可调整为图5a所示的姿态,通过驱动不同矢量推进器并控制其喷水电机转速,即可调整两栖机器人样机在水下以不同速度进行直行运动。根据图5a所示的矢量推进器姿态,实验中将只开启矢量推进器1的驱动方式称为模式1;将开启矢量推进器2和3的方式称为模式2;将同时开启矢量推进1、2、3的方式称为模式3;将矢量推进器1、2、3、4、5同时工作的方式称为模式4。机器人样机将分别在这4种驱动模式下进行直行运动,直行距离为2 m。在每种驱动模式下,矢量推进器的喷水电机将分别以2500,2750,3000,3250,3500 r/min的转速为机器人提供动力,其中3500 r/min是喷水电机的额定转速。图11a展示的是样机在模式3下且喷水电机以额定转速输出时机器人直线前行的过程。上述每组实验将重复5次用以统计机器人的平均速度。在4种驱动模式下样机的平均速度与转速的关系如图11b所示,实验结果表明,不同的矢量推进器驱动模式配合喷水电机转速控制可帮助两栖机器人样机在水下获得较广的直行速度范围。其中,在模式1下若矢量推进器的喷水电机以2500 r/min运行时,机器人的平均运行速度只有6.9 cm/s;在模式4下,若矢量推进器的喷水电机工作在额定转速下,它提供的推力可使机器人样机以20.4 cm/s的平均速度直行。此外,机器人样机在直行运动中这种低速与高速的转换只需改变矢量推进器的驱动模式和喷水电机的转速即可实现,控制过程相对简便。

(a)机器人直行过程(模式3,额定转速)
(b)不同模式不同转速下的平均速度图11 机器人水下直行实验Fig.11 Experiment of robot prototype moving forward
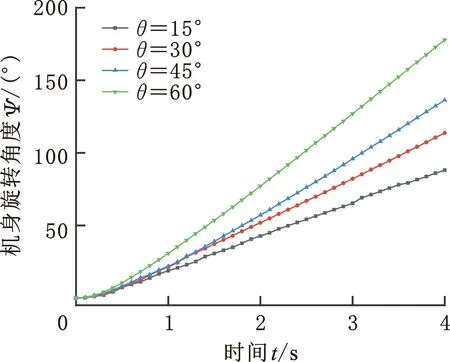
机器人样机在水下实现原地旋转运动,可参考图5b所示的矢量推进器的姿态。由于运动肢与其初始位置的夹角θ不同,因此其每组矢量推进器在机身产生的转矩不同,这将影响到机器人在原地转动的速度。考虑到每条运动肢在基节关节处的机械结构约束,其活动范围相对于初始位置最大转动为±60°,所以实验中分别选取了15°、30°、45°、60°四种情况,测试机器人样机在喷水电机额定转速下原地旋转情况。在每组实验下,机器人样机旋转4 s并通过自身搭载的陀螺仪记录其角度,每组实验重复5次。图12a展示了运动肢与其初始位置的夹角θ为60°时机器人样机原地逆时针旋转4 s的过程,不难发现由于机器人矢量推进器的姿态呈中心对称,因此其机身所受合力可使其在静水环境下原地旋转。图12b统计了机器人样机在运动肢与其初始位置的夹角θ为15°、30°、45°和60°时旋转角度与时间的关系。图12b所示的数据和实验预期一致,随着运动肢与其初始位置的角度增大,矢量推进器在机身产生的转矩增大,因而旋转角速度也随之增大,在夹角θ为60°时机器人样机的最大旋转角速度可达44.5°/s。

(a)机器人旋转过程(θ=60°)
(b)机器人旋转时其角度变化图12 机器人水下旋转实验Fig.12 Experiment of robot prototype rotating
基于图5c和图5d所示的矢量推进器姿态,机器人样机在水下上浮、下潜的运动过程如图13a所示。机器人在保持机身稳定的前提下,经过3 s可从距离水面51 cm处上浮至距离水面13.8 cm处。利用位于机器人机舱底部的压力传感器,图13b展示了上浮和下潜过程中样机当前距离水面深度随时间变化关系,该曲线在样机上浮过程中基本呈线性分布,这表明其运动具有较好的平稳性。

(a)机器人上浮下潜过程

(b)上浮下潜时机器人距水面深度变化图13 机器人上浮下潜实验Fig.13 Experiment of robot prototype surfing and diving
5 结论
本文基于部分仿生的设计思想研发了一款水陆两栖六足机器人。结合机器人的机械与电气设计,本文对两栖机器人进行陆地和水下的运动规划,并利用ADAMS运动学仿真,验证了机器人在不同斜坡路面爬行过程中的机身稳定性。为进一步评估机器人运动特性,本文搭建了机器人样机并进行性能测试实验。在陆地实验中,本文选取与仿真环境相同坡度的斜坡进行测试,实验结果表明机器人运动稳定且对不同坡度有较好的适应性。在水下实验中,通过配置矢量推进器的位姿,机器人实现了包括直行、旋转、上浮和下潜在内的多自由度运动,验证了它在水下运动的平稳性与灵活性。针对机器人应对陆地、水下及水陆过渡环境中的各项挑战,后续将在已搭建好的水陆两栖机器人平台上采用机器视觉等手段,实现水陆运动模式的自动切换并完成具有自主巡航功能的机器人运动控制策略。

