线切蓝宝石晶片面形质量评价方法的试验研究

王兰青 黄 辉 崔长彩

华侨大学制造工程研究院，厦门，361021

0 引言

随着光伏、微电子等行业的飞速发展，对蓝宝石、晶体硅、碳化硅等硬脆性材料的加工要求也日益提高[1]。硬脆性材料常见的加工制程为：切片-研磨-抛光[2]。目前常采用多线切割技术将其由晶棒变为晶片，随后通过研磨加工去除线切划痕，因此切割后的晶片质量对后续的研磨及抛光工艺有很大的影响。

国内外学者对线切后晶片的表面质量进行了大量研究。文献[3-5]对多线切割加工运动方式进行理论分析，通过调整加工工艺参数提高线切晶片的表面质量。文献[6]通过仿真研究多线锯切过程中的切削温度对切割后晶片表面翘曲度的影响规律。文献[7-8]对线网不同位置处的晶片表面质量进行检测，分析了线锯磨损对晶片表面质量的影响规律。文献[9]研究了工艺参数对单晶硅表面质量的影响规律。

在上述研究中，对线切后晶片面形质量的评价主要采用了抛光晶片的表面质量评价指标，包括总厚度偏差(total thickness variation TTV)、弯曲度(bow)、翘曲度(warp)。总厚度偏差值表征了加工后晶片最大厚度值与最小厚度值的绝对差值。晶片弯曲度是晶片中心点到参考平面的差值，反映晶片的凹凸程度。晶片翘曲度是用晶片中间面上的最高点与最低点的距离来表征晶片的翘曲程度。

线锯加工中，一方面在磨粒的作用下，晶片形成高低起伏的表面，另一方面受到加工过程中的机械应力及温度应力的综合作用[10]，晶片整体会产生弯曲变形。但现有的评价指标难以较好地统一表征线锯加工后的晶片面形质量。

本文针对目前线切晶片面形质量评价指标存在的问题，提出一种新型的线切晶片面形质量评价指标，给出了新评价指标的检测方法，并比较分析了不同工艺参数对线切片面形质量的影响规律。

1 线切片最小加工余量的计算

1.1 最小加工余量的定义及计算原理

本文提出以线切片的最小加工余量(minimum machining allowance，MMA)为线切片面形质量的评价指标。线切片最小加工余量是指在线切片内部寻找一组平行的平面(为假想的衬底片理想平面)，平面外侧部分是需要在后续研磨抛光中去除的加工余量，通过寻找合适的平行平面，保证其最外侧的加工余量最小。此时计算得到的外侧体积总和为最小加工余量，如图1所示。

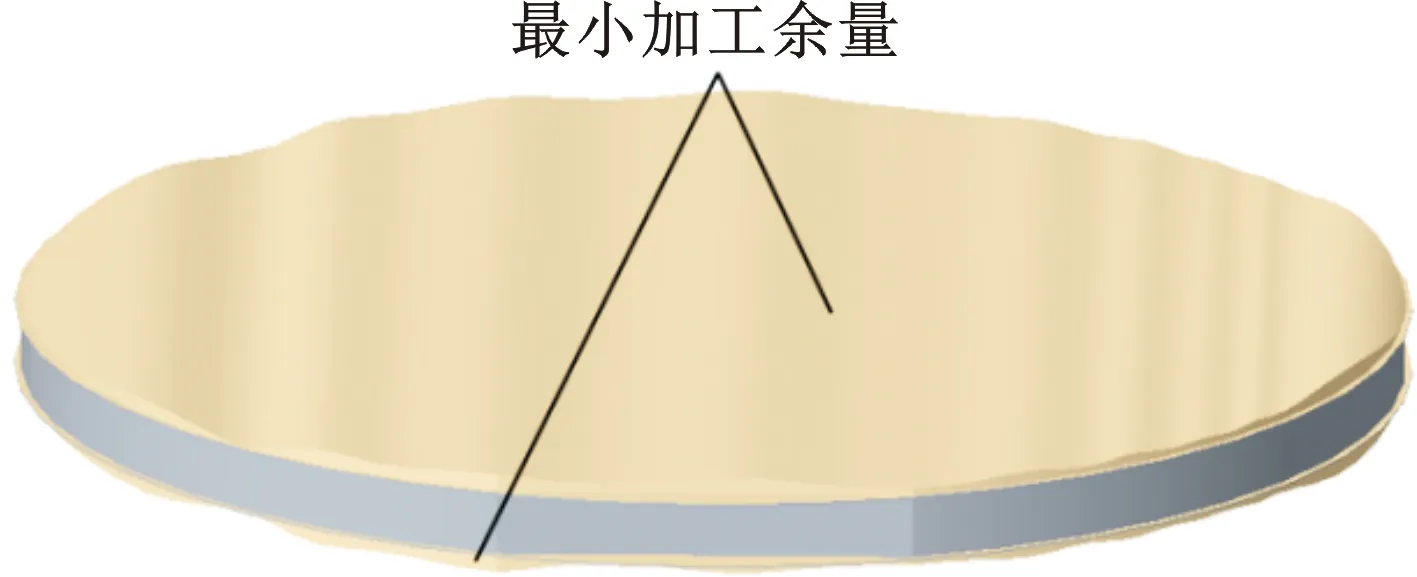
图1 线切片的最小加工余量Fig.1 MMA for wire saw wafer

线切片的MMA计算流程如图2所示。首先在晶片表面进行分区选点，对晶片每个点位置处上下表面进行精密测量；然后通过对检测点的拟合，得出晶片上下表面的形貌；由上下表面的极值点，做相应的平行平面，计算其外侧的工件体积量，从而获得MMA值。具体实施过程如下。

图2 MMA计算流程Fig.2 MMA calculation flow chart

晶片不受其他外力作用的情况下放置在一个可移动的晶片夹具上，晶片上下安装有两个传感器探头，可分别测量传感器到晶片表面的距离。其中上传感器探头到晶片上表面的距离为a，下传感器探头到晶片下表面的距离为b，如图3所示。上下传感器同时进行扫描，即可得到晶片不同位置处所对应的a、b值。

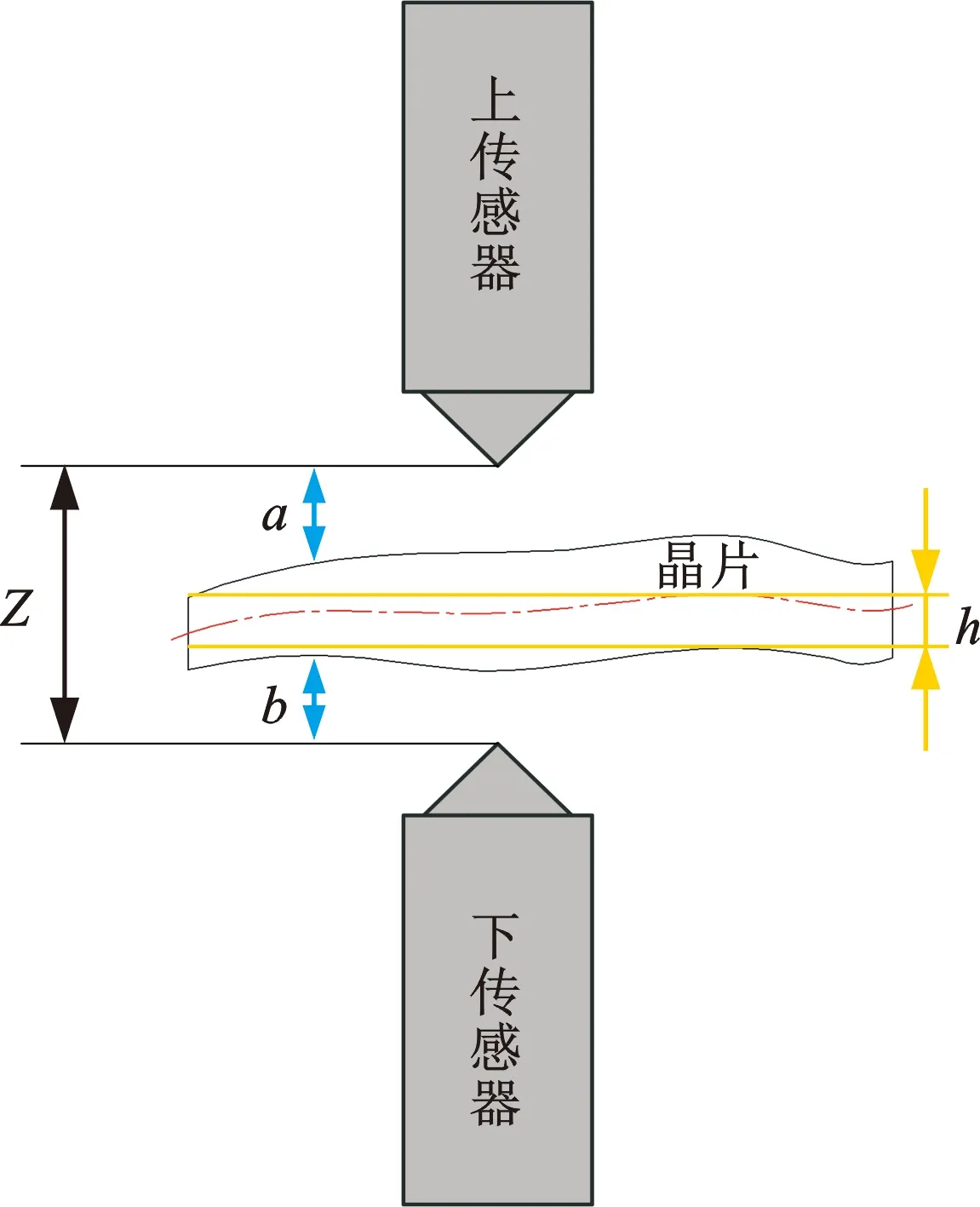
图3 线切片MMA检测原理图Fig.3 Schematic of wire saw wafer MMA detection

对所获得上下平面的点数据分别拟合，对得到的晶片进行找平处理，以消除因晶片放置引起的测量误差。对找平后的晶片上下表面分别积分，得到上表面与下表面对应的曲面体积Vup和Vdown：

Vup=∭(a1x2+b1y2+c1x+d1y+e1z+f1)dV

(1)

Vdown=∭(a2x2+b2y2+c2x+d2y+e2z+f2)dV

(2)

式中，x、y为晶片不同位置的测量点；z为晶片测量点所对应的高度值；a1、b1、c1、d1、e1、f1、a2、b2、c2、d2、e2、f2为拟合曲面参数；V为曲面总体积。

对两个曲面体积作差即可得到线切片体积：

VT=Vup-Vdown

(3)

通过上下表面的极值点(上表面的最低值amax和下表面的最高值bmax)做出两个平行的理想平面，将两个理想平面的间距定义为线切片理论上下表面间距h(图3)：

h=z-amax-bmax

(4)

式中，z为两传感器探头的间距。

在理想状态下，研磨后线切片厚度为h，此时线切片理论平整体积

VM=Sh

(5)

式中，S为理论线切片的底面积。

最小加工余量VMMA则为总体积VT和理论平整体积VM之差：

VMMA=VT-VM

(6)

1.2 最小加工余量的具体计算方法

试验以φ101.6 mm(4英寸)蓝宝石晶片为例，将线切片表面沿横纵方向20等分，在分割线的交点处进行采样测量，共计400个采样点，如图4所示。

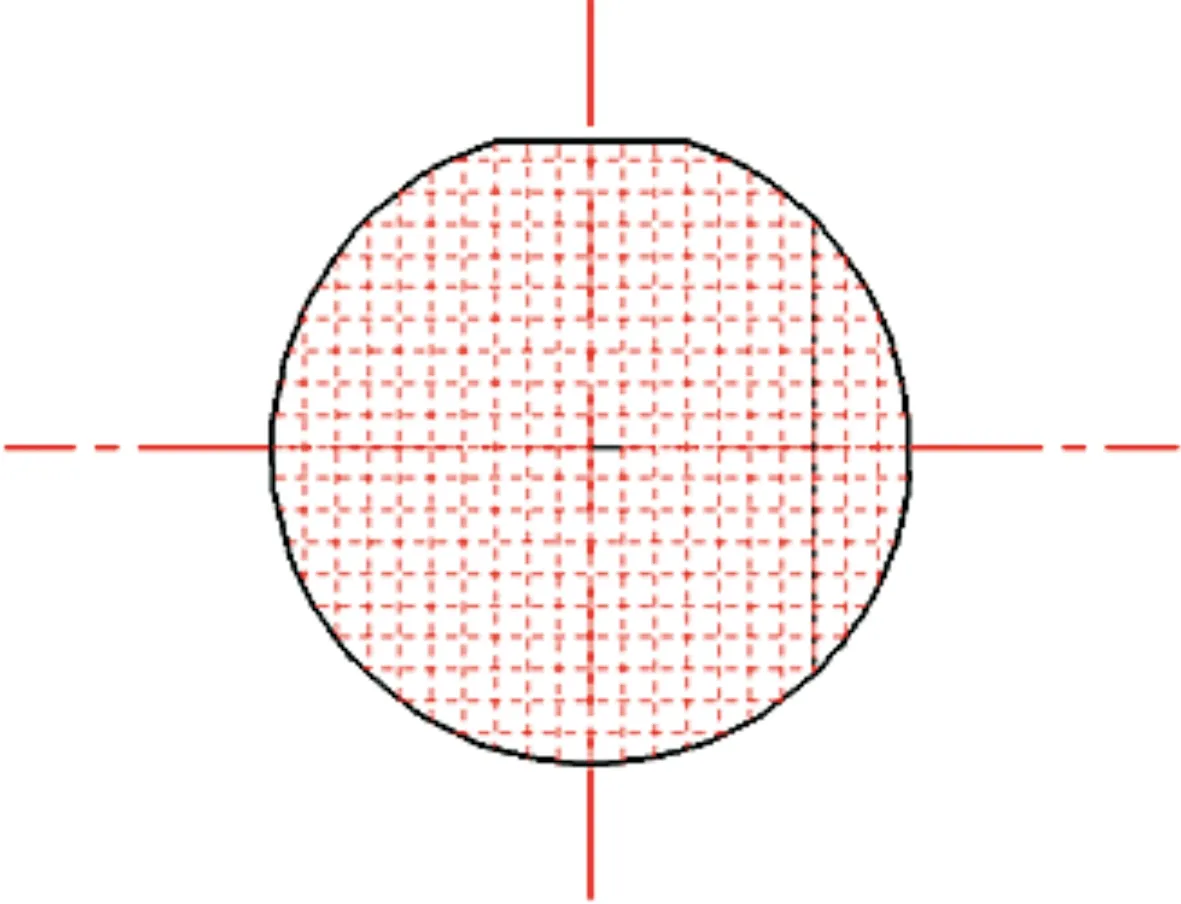
图4 线切片采样点示意图Fig.4 Schematic of sampling points for the wire saw wafer

在自行研制的衬底厚度检测仪上进行晶片采样，如图5所示。衬底厚度检测仪由上下两个激光位移传感器探头和一个X-Y数控工作台组成。激光位移传感器探头精度为0.01 μm。数控工作台可以控制晶片进行X、Y方向的平行移动(精度为0.01 mm)。将所需检测点坐标输入检测仪中，设备自动完成各检测点上下表面a、b值的测量。测量结果如图6所示。

图5 衬底厚度检测仪Fig.5 An instrument of wafer thickness detection

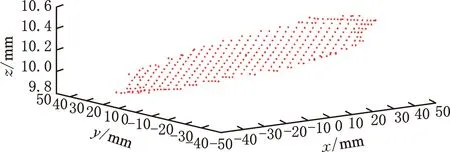
图6 晶片单面检测数据Fig.6 Single side detection data of the wafer

本文采用BP神经网络进行测量曲面拟合。神经元网络输入为不同位置处的距离测量值，输出为拟合曲面。神经元网络输入层与输出层已经给定，只需确定隐含层结构即可得到完整的神经元网络结构。隐含层节点数和层数的选取对拟合结果的准确度有很大影响。最佳隐含层节点参考公式如下：

(7)

式中，n为输入层节点数；l为隐含层节点数；m为输出层节点数；c为0～10的常数。

根据式(7)确定节点数的大致范围，并用试凑法确定最佳节点数和隐含层层数[11]。预测误差与隐含层节点数关系如图7所示。根据试凑结果，确定网络的隐含层层数为3，隐含层节点数为11，晶片单面的拟合曲面结果如图8所示。图9是根据上述方法所获得的同一晶片上下表面的拟合曲面。由图9可以看出，晶片表面呈现一定的倾斜，这主要是晶片的安装误差所致。因此在计算晶片MMA值前，需要对拟合面进行平面取平。

图7 不同隐含层节点数所对应的误差波动Fig.7 Error of nodes number in hidden layers

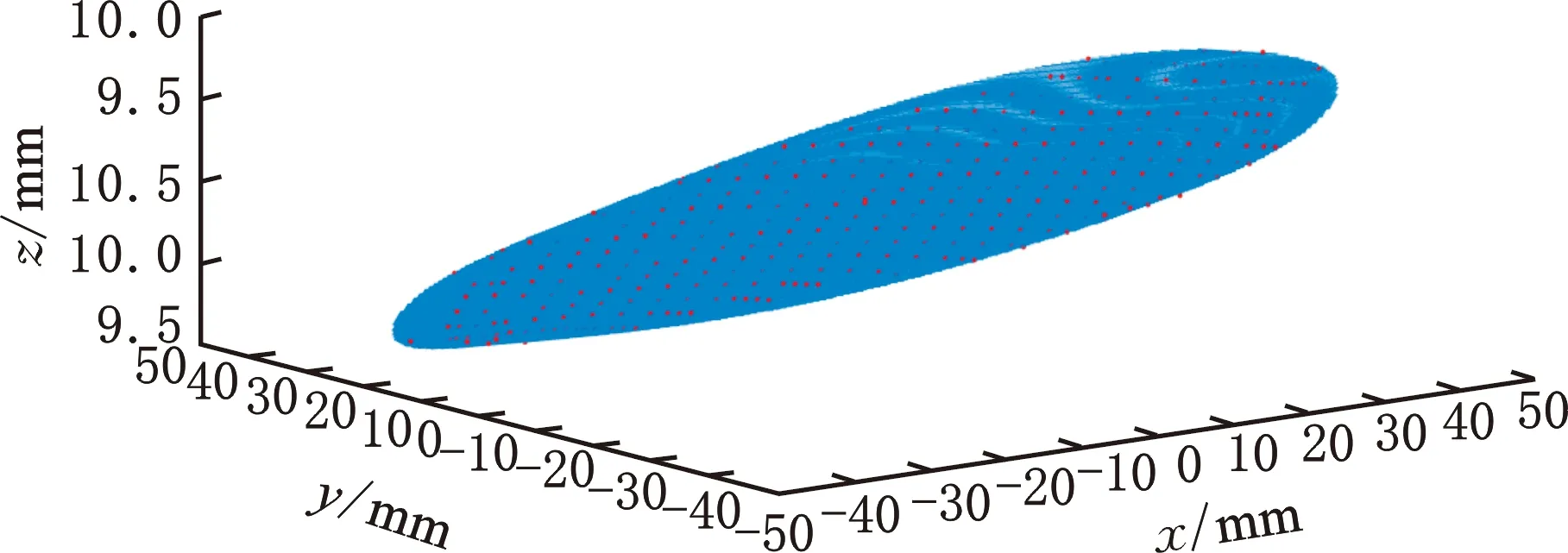
图8 晶片单面拟合结果Fig.8 Single side fitting result of the wafer

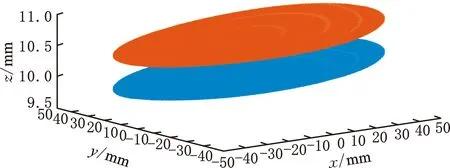
图9 晶片上下表面的拟合结果Fig.9 Fitting result of the wafer upper and lower sides

本文采用最小二乘法进行晶面取平，具体操作如下。将拟合后得到的晶片表面数据记为点集P={(xi，yi，zi)}。假设有一个拟合平面，其点集数据位于z=Ax+By+C平面，按最小二乘法确定该平面的点集W满足(zi-Axi-Byi-C)2。点集Q为点集P与点集W之差。对表面点集数据P求均值，并将其均值作为参考水平面高度H。将点集Q与参考水平高度H相加，即可完成对拟合曲面的晶面取平，取平后的结果见图10。利用MATLAB编程，根据式(6)计算出线切晶片的MMA。

图10 晶面取平后的拟合晶片表面Fig.10 Flattening result of the wafer upper and lower sides

2 锯切试验方案

切割试验采用X07M250×350-1D-O多线切割机，线槽间距0.75 mm，切割所用金刚石固结线锯线径基体为φ0.18 mm，磨粒大小30～40 μm。切割所用工件为长114 mm的蓝宝石晶棒，工件在定向后装夹于夹具上，加工过程中工件自上而下进给并且同时进行摇摆运动，试验装置如图11所示。

图11 多线切割试验装置Fig.11 Experimental setup of multi-wire sawing

本文采用单一变量法，通过改变切割过程中的不同工艺参数，得到不同工艺参数下的线切晶片。试验参数见表1[12]。

表1 切割试验参数Tab.1 Sawing parameters

一次切割加工可得152片晶片，从供线端开始每隔10片抽取一片晶片进行检测，一组工艺中共计取15片晶片进行检测。采用上文所述方法进行MMA值的检测。

3 试验结果

3.1 总耗线量的影响

图12所示是三组不同总耗线量下的MMA检测结果，其中t=360 min,θ=10°,F=45 N,vf=25 m/s。从图中可以看出，从供线端到收线端，晶片的MMA呈现先减小再逐渐增大的趋势。当总耗线量为2 km和2.5 km时，除了在供线端和收线端首尾有所波动外，其中间部分晶片的MMA大致呈线性增加；当总耗线量为3 km时，MMA从供线端到收线端呈现较为明显的波动。总体而言，随着总耗线量的减少，晶片的MMA逐渐减小，但减小幅度不大。

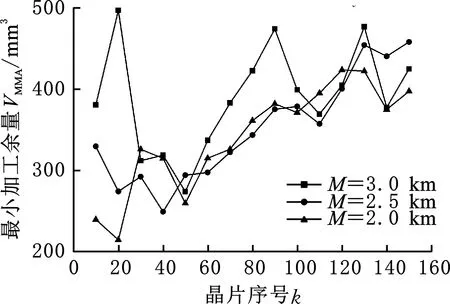
图12 不同总耗线量下的MMAFig.12 MMA with different total consumption wire

3.2 张紧力的影响

图13所示是三组不同张紧力下的MMA变化情况，其中t=360 min,M=3 km,θ=10°,vf=25 m/s。从图中可以看出，晶片的MMA值从供线端到收线端是先减小再逐渐增大，当张紧力为35 N时，MMA值从供线端到收线端大致保持稳定。总体而言，随着张紧力的减小，MMA值大致减小。

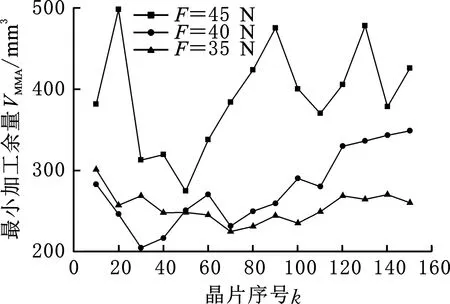
图13 不同张紧力下的MMAFig.13 MMA with different tensions

3.3 线速度的影响

图14所示是三组不同线速度下的MMA变化情况，其中t=360 min,M=3 km,θ=10°,F=45 N。从图中可以看出，晶片的MMA值从供线端到收线端先减小再增大。当线速度较高时，MMA值变化较大；当线速度减小到一定程度时，MMA值的变化不明显。

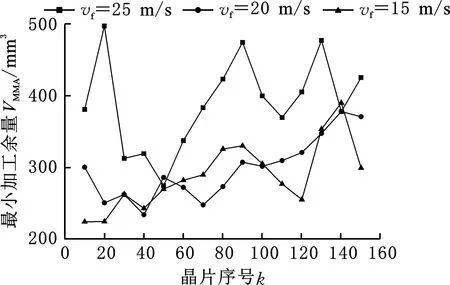
图14 不同线速度下的MMAFig.14 MMA with different wire speeds

3.4 总切割时间的影响

图15所示是两组不同总切割时间下MMA的检测结果，其中M=3 km,θ=10°,F=45 N,vf=25 m/s。从图中可以看出，晶片的MMA值从供线端到收线端的变化趋势与上文相似，都是先减小再增大。总切割时间为360 min时，MMA的变化起伏较大；当总切割时间增加时，MMA的变化减小。总体而言，随着总切割时间的增加，MMA值减小。

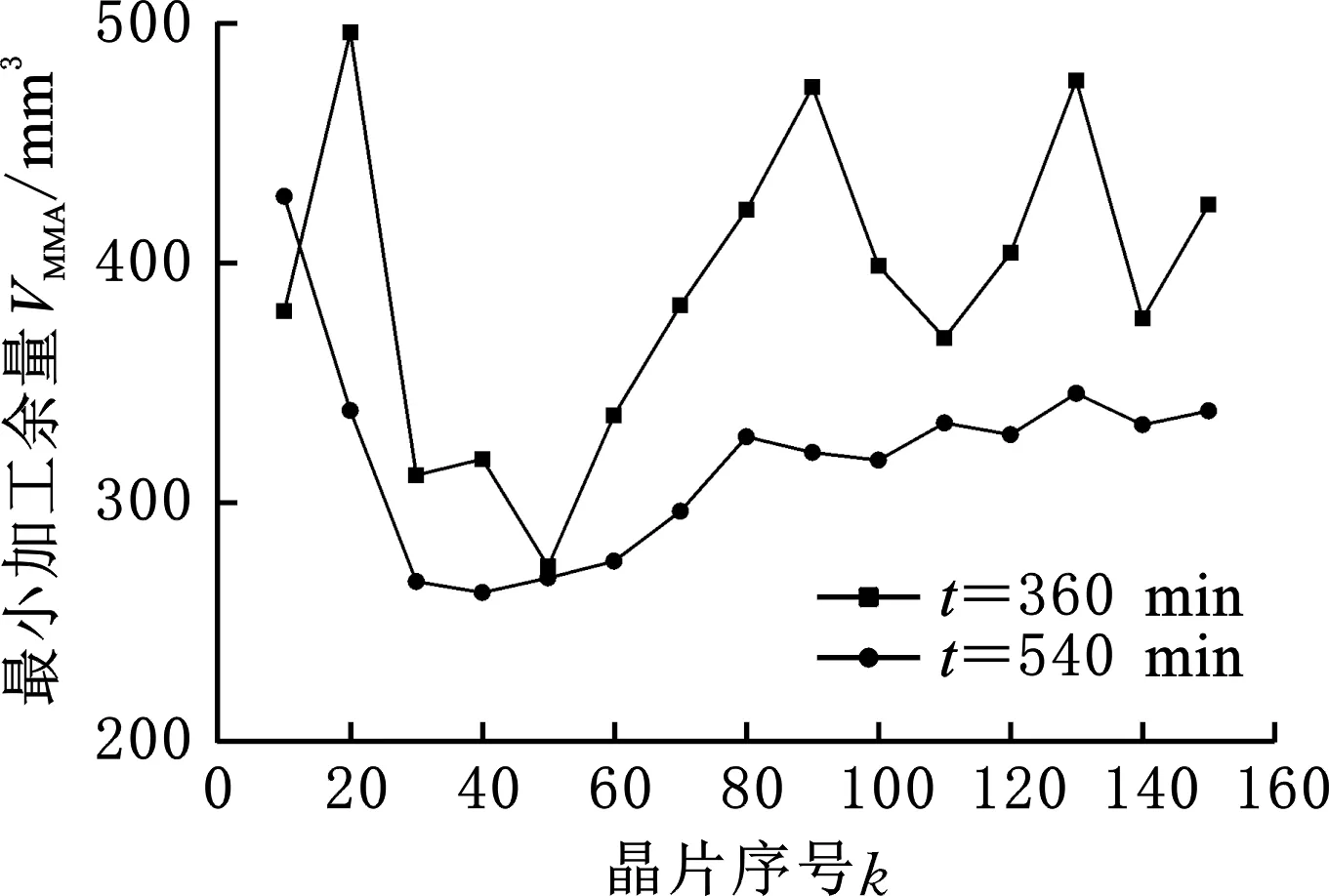
图15 不同总切割时间下的MMAFig.15 MMA with different total cutting time

3.5 摇摆角度的影响

图16所示是两组不同摇摆角度下的MMA变化情况，其中t=540 min,M=3 km,F=45 N,vf=25 m/s。从图中可以看出，晶片的MMA值从供线端到收线端的变化规律与上文相似。在大摇摆角度下，MMA值变化较为平稳；在小摇摆角度下，MMA值呈明显的线性增长。

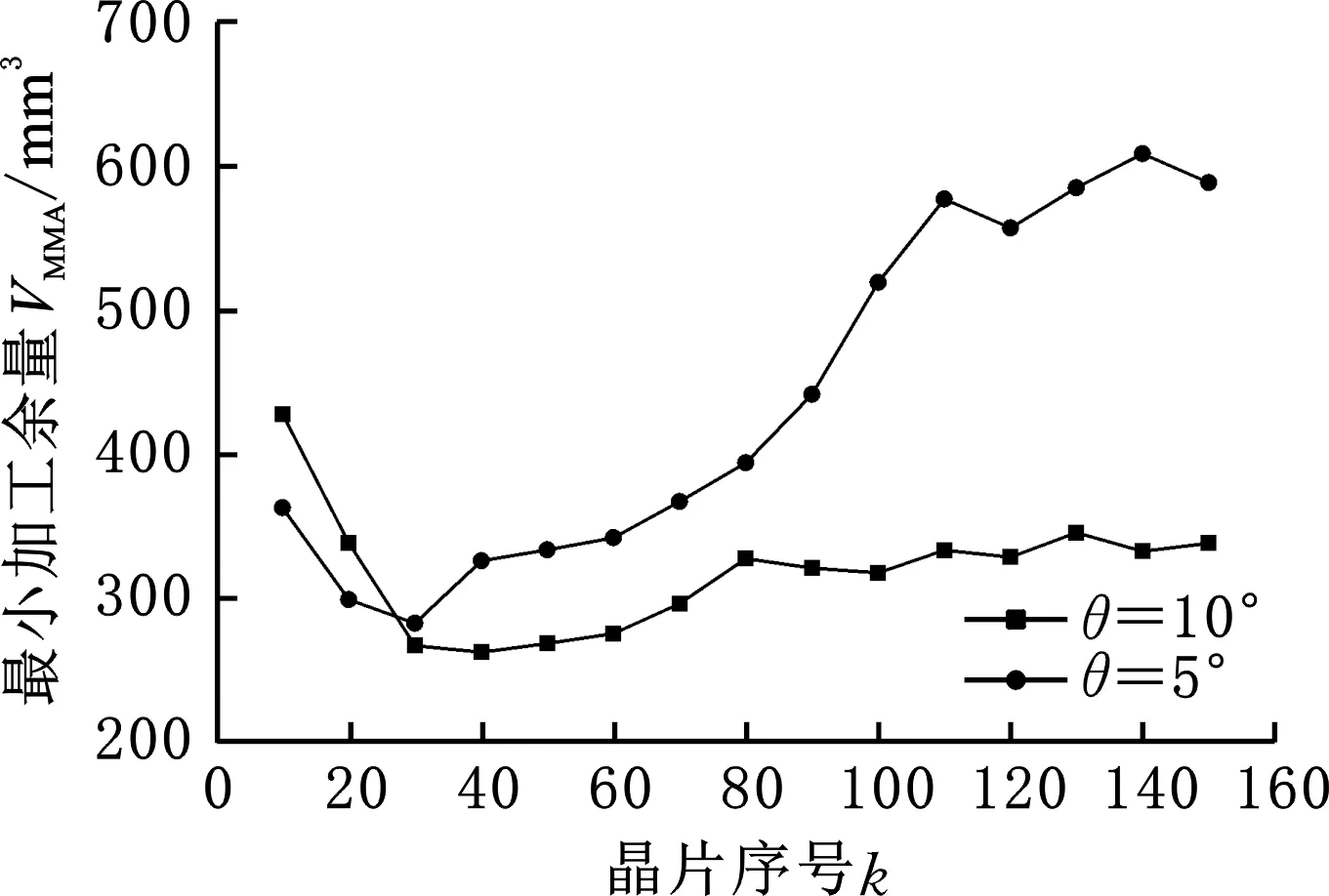
图16 不同摇摆角度下的MMAFig.16 MMA with different swing angles

4 讨论与分析

本文试验条件下蓝宝石线切片的总厚度偏差、弯曲度、翘曲度的测量值见文献[12]。试验结果表明，线切后蓝宝石晶片的总厚度偏差在5～20 μm波动，弯曲度在-25～25 μm波动，翘曲度在20～80 μm波动。常规的晶片面形质量评价体系与加工工艺参数中没有较好的对应关系，因此难以评价线切片的面形质量。

当加工机床确定时，线切片的加工面形质量主要受加工工艺参数以及线锯磨损的影响。结合图12～图16可以看出，在所有的加工条件下，MMA值从供线端到收线端都大致呈先减小后增大的变化趋势。与常规评价指标不同的是，MMA值基本与工艺参数的变化有一定的对应关系。相比而言，随着总耗线量的减小，张紧力的减小，线速度的减少，总切割时间的增加以及摇摆角度的增大，单片MMA的值都大致呈减小的趋势，与此同时，整个加工过程中晶片的面形质量也会更加稳定。试验得到的规律与实际生产加工的经验有较好的吻合性。

5 结论

本文针对切割加工晶片，提出了一种新的质量评价指标：线切片最小加工余量(MMA)，建立了一套完整的MMA评价方法。通过对不同加工参数下的线切蓝宝石晶片加工质量的综合检测发现：MMA值从供线端到收线端大致呈先减小后增大的趋势。MMA值反映了晶片加工后的表面质量变化，也包括了晶片的整体形状变化，是总厚度偏差和翘曲度的综合体现。在试验范围内，线切片MMA值基本与工艺参数的变化有较好的对应关系，因此可以更直观地反映锯切工艺参数的影响规律，更有效地为后续磨削加工提供参考依据。