砂糖橘体积及质量的线性回归分析*

应希源

（曲靖职业技术学院公共课教学部，云南 曲靖 655000）

0 引言

砂糖橘是生活中常见的水果，果实大小及质量是植物基因表达、生长状况等属性的表征，同时也是果实外在品质的表现。植物的生长状况及生长环境是影响植物果实发育、成长、成熟的重要因素，因此，通过图像技术对砂糖橘体积及质量进行预测，可以为植物生长状况分析、栽培管理优化等提供一定的参考，植物果实体积、质量的快速测量对研究植物特性和优质丰产培育具有重要意义[1-6]。

机器视觉无损检测分级是实现自动化分级的重要发展方向，而形状和重量是划分砂糖橘级别的重要指标，因此，对砂糖橘体积、质量进行线性回归分析，为自动化分级研究提供参考模型，具有一定的实际意义。

彭丽君[7]在球坐标的基础上对植物果实砂糖橘三维点云开展研究，对果实进行长宽高、体积精细测量，与测量值比较的平均误差分别为3 mm、2.3 mL。史燕山等[8]以苹果的纵径、横径、周长、纵径横径乘积分别与果实体积和果实重量进行了线性回归及一元非线性回归分析。张青等[9]通过多元线性回归分析建立了草莓重量分级模型，提出了一种基于机器视觉技术的草莓重量与形状分级方法。本文在此基础上，以市场上售卖的砂糖橘果实为材料，对纵径、横径、周长、横向投影面积分别与果实的体积和质量进行一元、多元线性回归分析，为植物生长状况分析及果实自动分级提供参考。

1 砂糖橘体积及质量的线性回归分析

采用图像法获取砂糖橘的纵径、横径、周长、横向投影面积数据，采用量筒、机械天平分别测得砂糖橘的体积及质量数据，再分别进行一元、多元线性回归分析。测量质量的天平型号为HC-TP11-2，最大称量200 g，分度值0.2 g。

图像法获取砂糖橘数据步骤如下：1）在A4白纸上打印一个2.0 cm×2.0 cm的正方形作为参照物，将砂糖橘编号后放置在A4纸上，再用手机在垂直上空居中位置拍照；2）打开PotoshopCS6软件，插入步骤1）所得图片，用“标尺”工具沿着正方形的水平位置画一条线段，点击“拉直图层”将图片调正；3）读取图像分辨率（本例为72像素/英寸），依次点击“图像”“分析”“设置测量比例”“自定”，像素长度设为“72”，逻辑长度设为“2.54”，逻辑单位设为“厘米”；4）调出“标尺工具”测量正方形的宽和高，再根据实际长度2.0 cm计算缩放比例后再调整图像大小，再测量参照物正方形的宽高，直至标尺测量长度为2.0 cm；5）用“快速选择”工具建立砂糖橘待测选区，依次点击“图像”“分析”“记录测量”便可得到纵径、横径、周长、横向投影面积数据，测量结束后再批量导出数据。

运用上述方法对某一品种的砂糖橘测量了30组数据作为实验样本。分别绘制砂糖橘体积概率分布图及砂糖橘质量概率分布图，从图1、图2可以看出砂糖橘体积、质量概率分布接近正态分布。从获取数据的散点图可以初步得出体积及质量与横径、纵径、横向投影面积呈线性关系。回归分析采用学生常用的办公软件：Microsoft Excel 2010，体积、质量分别用V（单位：cm3）、m（单位：g）表示，纵径（单位：cm）、横径（单位：cm）、周长（单位：cm）、横向投影面积（单位：cm2）分别用x1、x2、x3、x4表示。

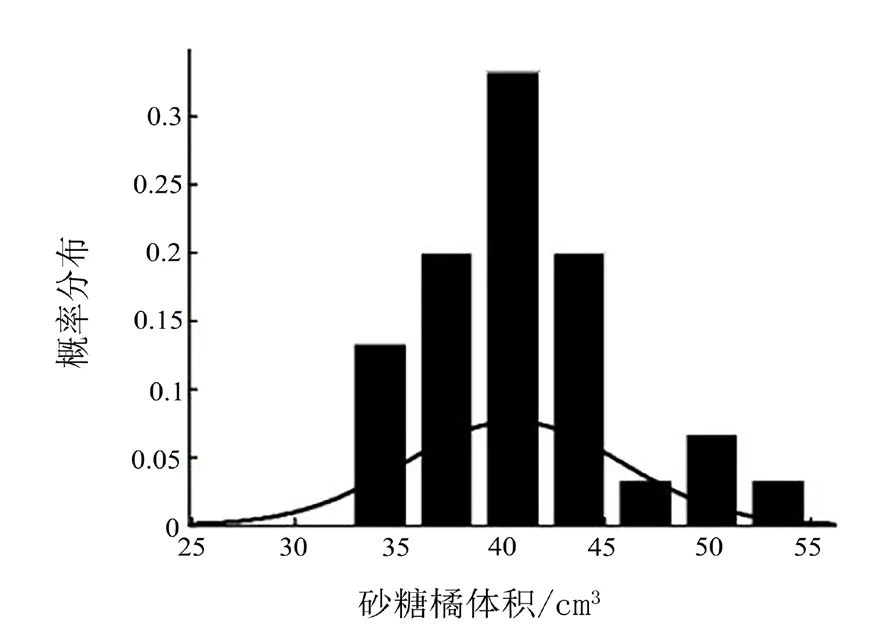
图1 砂糖橘体积概率分布图

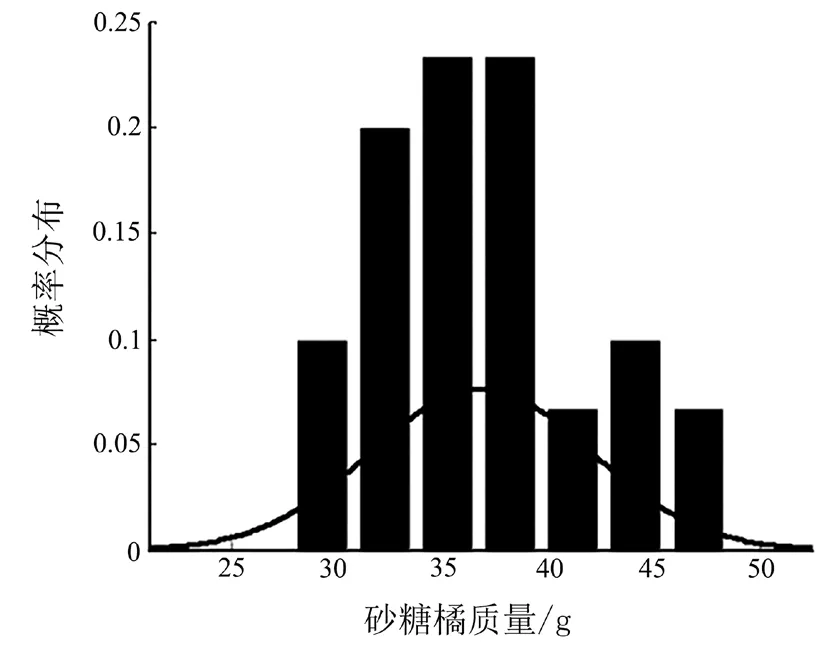
图2 砂糖橘质量概率分布图

1.1 砂糖橘体积及质量的一元线性回归分析

分别对砂糖橘体积V与x1、V与x2、V与x3、V与x4进行一元线性回归，置信度取95%，拟合结果如表1所示，从表1可以看出，砂糖橘体积与横向投影面积x4的拟合效果最好，具有显著的线性相关关系。根据参数F、Significanc F大小得出拟合模型通过F检验。拟合表达式V=-7.21+2.41x4为较优的一元线性拟合模型，在所选的变量中，砂糖橘体积受横向投影面积影响最大。

表1 砂糖橘体积一元线性拟合结果

砂糖橘质量的一元线性回归步骤与体积的一元线性回归步骤一致，经拟合检验后得到通过F检验的模型为m=-54.31+5.32x3，砂糖橘质量受周长影响最大。

1.2 砂糖橘体积及质量的多元线性回归分析

利用Microsoft Excel 2010的多元线性回归工具，对砂糖橘体积与纵径x1、横径x2、周长x3、横向投影面积x4四个变量建立体积模型，置信度取95%，拟合结果如表2所示，由Significance F值＜0.05可得模型通过F检验，但根据t检验的P-value值（简称“P值”）得出模型变量未通过t检验，因此将P值最大的变量x1删除后再重复进行拟合、检验，经4次拟合、检验后得到通过F检验及t检验的模型为V=-7.21+2.41x4。

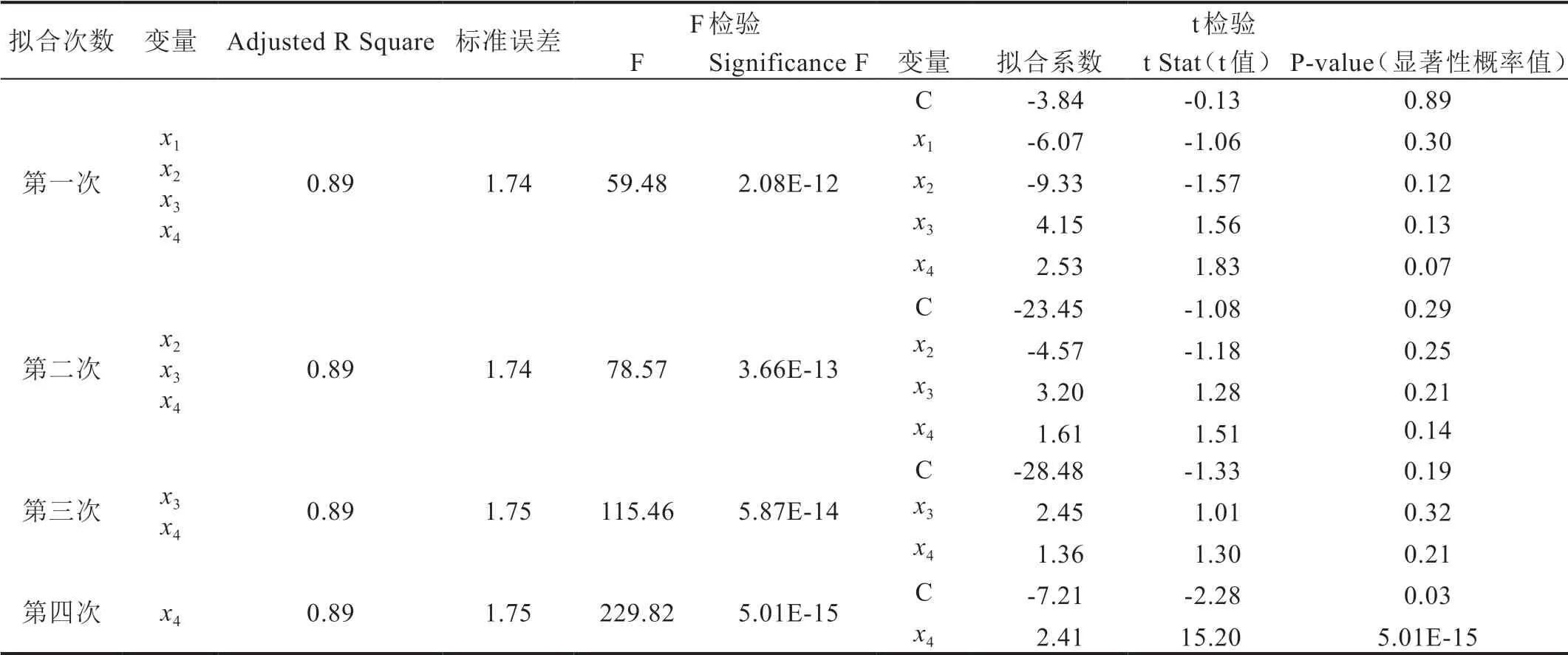
表2 砂糖橘体积多元线性拟合结果

砂糖橘质量的多元线性回归步骤与体积的多元线性回归步骤一致，经四次拟合检验后得到通过F检验、t检验的模型为m=-54.31+5.32x3。

1.3 线性回归模型讨论

对砂糖橘体积、质量进行多元线性回归时，体积、质量对全变量多元回归得到的模型均通过F检验，说明回归方程总体是线性相关的，但并不能说明回归方程中所有自变量都对因变量有显著影响[10]，因此还要对回归系数进行t检验。若自变量对应的P值未大于0.05，则该自变量未通过t检验，此时采用后退法，将P值最大的变量删除后再进行回归检验，直至回归模型同时通过F检验及t检验。在本例中，直至剩余自变量为1个时，回归总体方程及系数才通过F检验及t检验，出现此种情况，主要因为刚开始选取的自变量中存在多重共线性。采用逐步删除变量方法进行多元线性回归后得到的较优模型与一元线性回归比较得到的较优模型一致，较优的体积模型为V=-7.21+2.41x4，较优的质量模型为m=-54.31+5.32x3，也即砂糖橘的体积与横向投影面积显著相关，砂糖橘的质量与投影面的周长显著相关。

2 模型预测结果分析

采用线性回归分析得出的较优体积、质量模型对砂糖橘的体积及质量进行预测。具体步骤为：1）选取该品种的10个砂糖橘，通过测量获取体积、质量、周长、横向投影面积数据；2）将砂糖橘的横向投影面积代入体积模型、将周长代入质量模型，计算出砂糖橘的体积及质量；3）将计算值与测量值进行比较。模型预测结果如表3所示，线性回归模型预测砂糖橘体积及质量与测量值比较的平均相对误差分别为4.94%、6.52%。

表3 较优一元及多元线性回归模型的预测结果

3 结论

对某一品种砂糖橘的体积及质量分别进行了一元及多元线性回归，得出较优体积模型为V=-7.21+2.41x4，较优质量模型为m=-54.31+5.32x3。并将模型计算值与测量值进行了比较，得出模型体积预测值、质量预测值与测量值比较的平均相对误差分别为4.94%、6.52%。对于其他品种砂糖橘的体积及质量模型还需进一步验证。