基于和声搜索优化支持向量回归的软件可靠性预测

汪顺和

(安徽开放大学 学习资源中心,合肥 230022)

一、引言

软件可靠性 (Software Reliability )是软件产品在规定的条件下和规定的时间区间完成规定功能的能力。规定的条件是指直接与软件运行相关的使用该软件的计算机系统的状态和软件的输入条件，或统称为软件运行时的外部输入条件；规定的时间区间是指软件的实际运行时间区间；规定功能是指为提供给定的服务，软件产品所必须具备的功能。软件可靠性不但与软件存在的缺陷和(或)差错有关，而且与系统输入和系统使用有关。

软件可靠性模型就是根据已发生的软件失效数据，通过统计方法计算出软件的可靠性估计值或预测值[1]。它是评估和预测软件可靠性的重要工具，对于软件可靠性的评估起着核心作用，从而对软件质量的保证有着重要的意义，也为改善软件质量提供了指南。张坤等人使用神经网络对软件可靠性建模[2]，张婷婷等人[3]建立了贝叶斯组合模型用来提高模型的预测精度和模型的适应性，李思雨等人[3]利用极限学习机对软件可靠性建模，将经典软件可靠性模型和人工智能算法有机结合。

和声搜索(Harmony Search，简称HS)算法[5]是Greem提出的一种新型启发式优化算法。类似于遗传算法对生物进化的模仿、模拟退火算法对物理退火的模拟以及粒子群优化算法对鸟群的模仿等。和声算法模拟了音乐演奏的原理，在音乐演奏中，乐师们凭借自己的记忆，通过反复调整乐队中各乐器的音调，最终达到一个美妙的和声状态。该算法简单，易于与其他算法混合，构造出具有更优性能的算法[4]，在参数寻优问题上有很大的优势。

支持向量机[6](Support Vector Machine，简称SVM)由Vapnik首先提出，它是一种监督式学习的方法，广泛地应用于统计分类以及回归分析中。该方法理论基础是统计学习理论，可用于模式识别和回归问题，能提供很好的全局最优性和泛化能力。SVM的关键在于核函数的选择、SVM中参数和核函数中参数难以确定。传统的方法有：实验法、经验选择法、交叉验证法等，其中交叉验证法使用较多。近年来，启发式算法已被成功地应用到SVM参数优化中来，如遗传算法、粒子群算法、模拟退火算法。本文利用和声搜索算法参数寻优的优点，用来优化支持向量回归中的参数，并将之用于软件可靠性预测，提出了一种基于和声搜索优化支持向量回归的软件可靠性预测模型，并通过实验证明该方法的可行性和有效性。

二、算法原理

(一)支持向量回归(Support Vector Regression, SVR)

SVM作为一种监督式学习的方法，其理论基础是统计学习理论，既可以用于模式识别，又可以用于回归问题。这两方面上本质是相同的，都有一个可以是属性矩阵或者是自变量的输入x，也都有一个输出y。模式识别输出是分类标签的，回归输出是因变量，即相当于一个函数映射y=f(x)。利用训练集中已知数据(x，y)来建立模型，再利用这个模型去对测试集进行分类或者回归。研究表明，SVM在回归问题上也具有极好的性能。

设给定训练集{(xi,yi)}∈Rn×R,i=1,2，…,l。

对于线性回归，采用f(x)=w·x+b作为回归函数，其中w表示权重向量，b表示偏项，目标就是寻找合适的w和b，使得f(xi)估计yi时的估计误差最小，即回归风险最小。采用ε-不敏感损失函数，回归问题转化为：

s.t.wTxi+b-yi≤ε+ξi

(1)

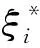
引入Lagrange函数，公式(1)可以转化为其对偶问题：

(2)

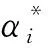
对于非线性回归，首先将输入数据集映射到一个高维特征空间中，紧接着在高维特征空间中进行线性回归，这其中需要构造一个非线性映射。只需要将公式(2)中的(xi,xj)用核函数K(xi,xj)代替。因此，非线性回归的优化问题为：

(3)

在线性不可分的情况下，将最优化问题转化为二重QP问题，在原空间得到如下非线性判定函数：

(4)

(二) 标准和声搜索算法(Harmony Search，HS)

HS算法模拟音乐家创作的过程：HS算法中将每次演奏的和声类比于每次迭代的解向量；和声中的音调类比解向量中的分量；美学评价类比目标函数；最佳的和声类比全局最优。首先，算法产生N个初始解(和声)放入和声记忆库HM内，以概率HMCR在HM内搜索新解，以概率1-HMCR在HM外变量可能值域中搜索。然后，算法以概率PAR对新解产生局部扰动，判断新解目标函数值是否优于HM内的最差解，若是，则替换之；再不断迭代，直至达到预定迭代次数Ni为止。HS算法中参数有：决策变量的个数N，各个决策变量的取值范围[Li,Ui]，和声记忆库大小HMS，和声记忆库取值概率HMCR，音调微调概率PAR，音调微调带宽BW，最大迭代次数Ni。HS具体的算法步骤如下：

Step 1确定目标函数和初始化参数。

Step2初始化和声记忆库，并计算目标函数值。

在每个决策变量取值范围内，随机生成HMS个解向量放入和声记忆库HM中，每个决策变量按照以下公式生成：

(5)

其中i=1，2，…，N，k=1，2，…，HMS；

Step3产生一个新和声(即新解)。

新和声x′=(x′1,x′2,…,x′N)中任一音调(即变量)x′i按照如下规则产生：首先产生一个0到1之间的随机数rand1，如果rand1小于和声记忆库取值概率HMCR，则在和声记忆库中HM个第i维变量中随机选择一个，然后产生一个0到1之间的随机数rand2，如果rand2小于音调微调概率PAR，按照公式(6)进行局部干扰；如果rand1大于和声记忆库取值概率HMCR，则按照公式(5)随机产生一个新解。

x′i=x′i+rand2*BW

(6)

Step4若Step3中的新解优于HM中的最差和声，则将新解x′替换HM中当前最差和声，更新和声记忆库HM。

Step5判断算法终止条件，若满足，则停止迭代，输出最优解；否则重复步骤Step3和Step4。

(三)基于和声搜索优化支持向量回归(HS-SVR)的软件可靠性预测

构造出一个具有良好性能的SVM，核函数的选择是关键。核函数的选择包括两部分工作：一是核函数类型的选择，二是确定核函数类型后相关参数的选择。常用的核函数有线性核函数，多项式核函数，径向基核函数，Sigmoid核函数。

径向基核函数也叫高斯核函数，是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，是应用最广的一个核函数，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少。本文基于 HS-SVM的软件可靠性预测模型选取径向基核函数作为核函数，公式(7)是其表达式，将公式(3)中的K(xi,xj)替换成公式(7)。模型中需 要 优化 的 参 数 有 惩 罚 因 子C、核函数参数σ及损失函数中的ε，采用和声搜索算法来优化参数C、σ和ε。

(7)

其中，σ是高斯核的宽度，其值大于0。

和声搜索算法优化支持向量回归模型中参数时，将参数(C,σ,ε)看作为和声，即问题的解，回归指标均方差作为HS算法中的目标函数，当目标函数最小时所对应的解(C,σ,ε)是最优的。基于和声搜索算法的支持向量回归(HS-SVR)的软件可靠性预测建立的步骤如下：

(1)对选定的失效数据进行归一化处理，确定训练样本数据和预测样本数据；

(2)选择SVM模型中的回归指标均方差作为HS算法中的目标函数；

(3)初始化和声算法的参数和C、σ和ε的取值范围；

(4)将训练样本数据代入目标函数，得到C、σ和ε的最佳组合值(CO,σO,εO)；

(5)将最佳组合值(CO,σO,εO)代入SVM模型中， 预测测试样本值。

三、仿真实验及结果分析

(一) 仿真实验

为了验证本文提出模型的可行性和有效性，实验选择两组真实故障数据SYS1和SYS2作为测试数据，两组数据均来自Muse数据集[7]。SY1数据中有136条记录，SYS2数据中有86条记录。两组数据中每一条记录由两列构成，第一列是故障编号，第二列是当前故障与上次故障发生的时间间隔。

实验前两组数据中的第二列数据转化为累计时间，然后对故障数和连续时间进行归一化处理，SYS1中取前90条数据作为训练样本，SY2中取前56条数据作为训练样本，两组数据中剩下部分作为预测样本。实验平台采用Matlab2013，实验中和声搜索算法参数设置为HMS=5，HMCR=0.95，PAR=0.5，BW=0.01，Ni=200。算法独立运行10次，取均方差最小所对应的参数为最终参数。均方差值越小，说明参数估计的精确度越高。将得到的最佳参数代入模型，对测试集进行预测，再与真实值进行比较。仿真实验结果如表1所示，表1、表2和表3中的G-O和M-O模型的数据来自参考文献[8]。

表1 两组数据对应的模型中的参数

(二) 结果分析

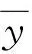
均方差是误差平方的平均数，则均方差定义为：

(8)

平方相关系数，以R2表示。R2提供了吻合度相关信息，用来评价预测模型的好坏。R2的值表示模型预测值真实值相吻合的程度，值越大吻合度越高。平方相关系数定义为：

(9)

由表1可以得出，用和声搜索算法优化支持向量回归中的参数方法效果很好，没有拟合不出来的情况，说明本文提出的软件可靠性预测模型是可行的。

对于G-O模型和M-O模型,以故障数据向量和失效累计时间向量作为输入量,利用和声搜索算法进行参数估计，参数估计结果见表1。利用三种模型分别对相同的训练数据和测试数据进行分析计算,计算结果见表2和表3。可以看出，HS-SVR模型与G-O模型和M-O模型相比，HS-SVR模型的均方差最小，平方相关系数最大，这说明模型的预测能力和吻合度非常好。

表2 SYS1的训练误差及预测误差

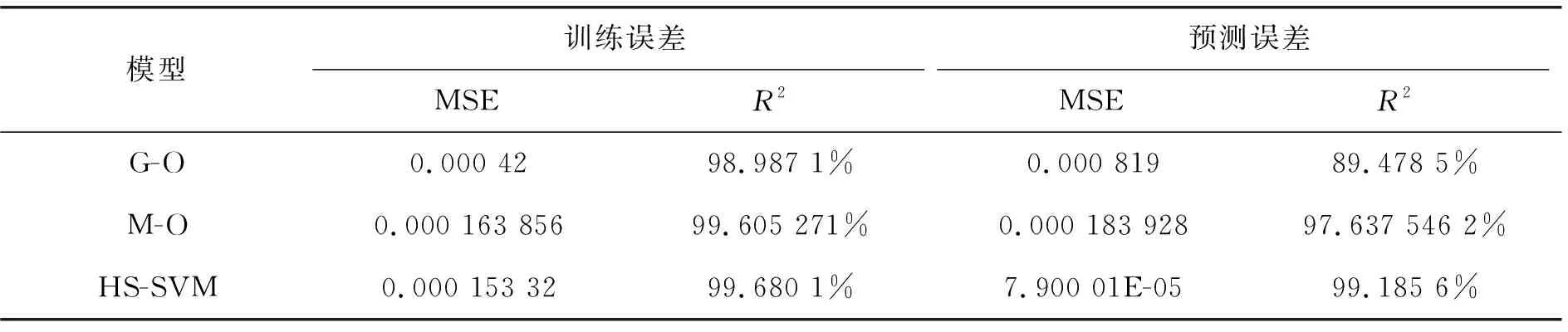
表3 SYS2的训练误差及预测误差

G-O模型的均值函数：

μ(t)=a(1-e-bt)

(10)

M-O模型的均值函数：

μ(t)=ln(λθt+1)/θ

(11)

其中，μ(t)表示截止到t时刻检测到错误数的期望值，t表示错误发现的时刻，a、b、λ、θ是未知参数。

将本文提出的HS-SVR模型、G-O模型、M-O模型各自生成的曲线和原始数据点进行对比，如图1、图2所示，可以发现，模型曲线和原始观测数据点非常接近,仅有少量的偏离,说明模型的吻合度非常好,预测能力非常强,优于其他两种模型。

四、结论

软件可靠性模型是评估和预测软件可靠性的重要工具，支持向量回归在小样本数据预测中具有较为突出优势。本文为了提高软件可靠性预测的精确度，提出了一种基于和声搜索优化支持向量回归的软件可靠性预测模型，并通过两组数据进行实验，证实了模型的有效性。将实验结果与两个经典软件可靠性模型做比较，结果表明，该模型具有较好的预测效果。文中的方法原理简单，容易实现，也可以运用到其他应用中，具有一定的通用性。