基于路段转移采样的最优路径集计算方法

李 军， 郭育炜， 叶 威

(中山大学智能工程学院/广东省智能交通系统重点实验室， 广州 510006)

路径选择是出行行为研究的一个热点问题[1]，对于路径诱导、出行行为分析、交通管理与规划具有重要意义。随着现阶段交通大数据以及计算机技术的发展，利用历史数据驱动来进行最优路径计算具有较高计算效率，逐渐成为当前研究与应用的主流。

当前路径选择研究中，基于Markov过程是一类主要方法，即依据节点或路段之间的位置转移来建立路径选择过程[2-4]。现阶段通过视频监控、GPS和手机定位等技术获取的交叉口车辆转向比例是较简便的工作，有学者依据历史数据获取的交叉口转向比例来建立路径选择方法[5-7]；有学者提出基于区域与时段划分来计算转向比例，并设计最大概率路径求解算法来计算最优路径[8]。然而在实际需求中，往往需要将路径选择从一条扩展到多条[9]。首先，出行者对于“最优”的认知存在偏差，每个出行者都有自身选择的最优路径；其次，每个出行者的每次出行往往是在多条路径中进行选择，每次选择不一定相同。对于给定的出行起点和终点，出行者可选择的“最优路径”虽然很多，但选择频率最高的往往只有数条，这些路径在本研究中被定义为最优路径集。随着交通大数据以及计算技术的发展，如何获取多条最优路径已被广泛研究[10]。其中，最短路径问题是研究最多的最优路径问题。例如：对Dijkstra方法进行改进，以计算K条最短路径[11]；采用KSP相关算法，在获取最短路径的基础上计算次短、再次短路径[12]等。然而，已有的对于多条最优路径的研究均基于路段阻抗来实现，而由于交通状况的复杂性，获取路段阻抗有较大难度；并且在实际应用中未考虑两方面问题：一是交通状况随时间变化的影响；二是路网中起点与终点数量巨大，特定点对之间数据量不足。

通过交通大数据获取路段间转移概率是较简便的过程。对于多条路径计算，依据概率采样是较适合的方法：首先，基于转移概率，从起点向终点逐步对路段进行采样来获取完整轨迹[13-15]；然后，对采样得到的轨迹进行统计，得到最优路径集。本文基于概率采样的思想，提出了基于路段间转移概率进行轨迹采样来获取最优路径集的方法(最优路径集路段转移概率法)：首先，依据交通小区之间在不同时段下的路段间转移概率，提出路段转移采样方法；然后，设计基于路段转移采样的轨迹采样算法，并给出最优路径集收敛规则。该方法一方面避免了对阻抗的计算；另一方面考虑了交通状况随时间变化的影响，且避免特定点对之间数据量不足的问题。最后以广州市越秀区的1个案例对方法的有效性进行验证。

1 最优路径集路段转移概率法

将路网表示为G=(V,A)。其中，V={vi|i=1,2,…,IV}为节点集合，vi为任意一个节点，IV为节点数量；A={al|l=1,2,…,IA}为路段集合，al为任意一个路段，IA为路段数量。

为避免起点与终点之间数据量不足的问题，将给定的点扩展到交通小区，将起点r、终点s所在区域分别记为交通小区O、D。由于不同时段的交通特征具有差异性，本研究根据交通状况随时间的变化进行时段划分。利用从交通小区O到交通小区D在分时段下的历史的出行轨迹数据计算交叉口车辆转向比例，称其为路段间转移概率。假设有路段ai与aj(i,j{1,2,…,IA},i≠j)，记路段ai到路段aj的转移概率为如图1A所示，路段a1向下游路段a2、a3、a4的转移概率分别为满足[0,1]，且

由于起点为一个点，因此还需定义由起点r选择某一个起始路段的概率为起始概率，可由历史的出行轨迹数据统计得到。假设路段al(l{1,2,…,IA})为起点r的一个起始路段，将选择al的概率记为如图1B所示，起点r选择路段a1、a2、a3的起始概率分别为满足[0,1]，且

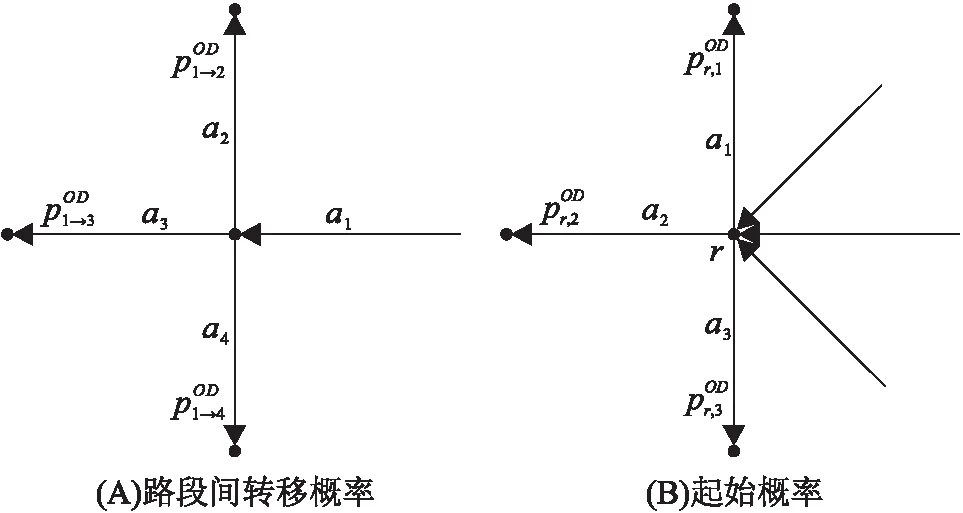
图1 转移概率示意图

本研究利用交通小区之间在分时段下的路段转移概率，计算起点到终点的最优路径集。最优路径集路段转移概率法包括3个部分：一是根据路段转移概率，进行路段间的转移采样；二是设计基于路段转移采样的轨迹采样方法；三是基于轨迹采样，给出最优路径集的收敛规则。

1.1 路段转移采样方法

1.1.1 起始路段采样 对于起点r，用n(r)表示r的起始路段数量，将起始路段表示为al1,al2,…,aln(r)(l1,l2,…,ln(r){1,2,…,IA})，起始概率表示为具体步骤如下：

Step 1：将[0,1]分成n(r)个子区间W1,W2,…,Wn(r)，每个子区间长度与对应起始路段的起始概率值相等，即

(1)

Step 2：产生一个在[0,1]上服从均匀分布的随机数q。

Step 3：判断q所在的子区间，若qWu(u{1,2,…,n(r)})，则该子区间对应的路段alu即为采样得到的起始路段。

1.1.2 路段间转移采样 对于一个路段ai(i{1,2,…,IA})，用m(ai)表示ai的下游路段数量，将下游路段表示为aj1,aj2,…,ajm(ai)(j1,j2,…,jm(ai){1,2,…,IA})，各下游路段转移概率分别为则路段间转移采样的具体步骤如下：

Step 1：将[0,1]分成m(ai)个子区间U1,U2,U3,…,Um(ai)，每个子区间长度与对应下游路段的转移概率值相等，即

(2)

Step 2：产生一个在[0,1]上服从均匀分布的随机数w。

Step 3：判断w所在的子区间，若wUk(k{1,2,…,m(ai)})，则该子区间对应的路段ajk即为采样得到的下游路段。

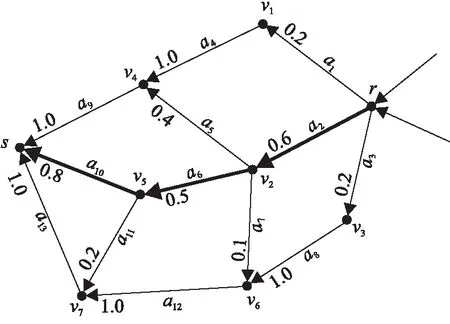
图2 路段转移采样示意图

1.2 轨迹采样方法

由起点r逐步执行起始路段采样、路段间转移采样，将前一步采样所得路段作为当前路段(用a′表示)来采样下游路段，直到到达终点s，结束采样。每一步采样均记录所得下游节点的前一个节点(用λ(vi)表示节点vi的前一个节点)；采样结束时，由终点s向起点r依次回溯搜索记录的节点，并顺次连接起来，获得从起点r到终点s的采样轨迹。若采样过程出现以下情况，则重新由起点r开始采样：一是转移次数(用n′表示)达到某个上限值(设为T次)仍未到达终点s；二是采样过程中因某个路段向下游路段转移的路段数据缺失而导致无法继续采样。具体步骤如下：

Step 1：按照起始路段采样方法，将采样所得起始路段记为ac；记路段ac的末端节点为H(ac)，记录节点H(ac)的前一个节点λ(H(ac))为起点r，记路段a′为当前路段ac，令n′=1。

Step 2：按照路段间转移采样方法，将由当前路段a′采样所得下游路段记为ah；记路段ah的首端节点为G(ah)、末端节点为H(ah)，记录节点H(ah)的前一个节点λ(H(ah))为G(ah)，令n′=n′+1。若当前路段a′向下游路段转移的路段数据缺失，则返回Step 1重新采样。

Step 3：判断H(ah)=s是否成立？若成立，则记终点s的前一个节点λ(s)为G(ah)，进入Step 5；否则，进入Step 4。

Step 4：判断n′≥T是否满足？若满足，重新开始Step 1；否则，令a′=ah，返回Step 2。

Step 5：由终点s开始，依次搜索前一个节点，记为vg1,vg2,…,vgx(vg1=λ(s),vg2=λ(vg1),…,vgx=λ(vgx-1),r=λ(vgx))，则采样轨迹为：r→vgx→vgx-1→…→vg2→vg1→s。

以图2为例，要采样获得轨迹L:r→a2→a6→a10→s，需依次实现：(1)由起点r采样得到路段a2；(2)由路段a2采样得到路段a6；(3)由路段a6采样得到路段a10并到达终点s。

1.3 最优路径集计算方法

用C表示所有生成轨迹的集合，用Ri表示集合C中出现频率(对应同一路径的轨迹数量占采样轨迹总数的比例)排在第i位的路径，则出现频率排名前K位的路径所组成的集合ZK={R1,R2,…,RK}为本研究希望获得的最优路径集。由于采样的随机性，最优路径集可能随采样而变化，但会随着采样次数的增加而逐步趋于稳定，所以，本研究采用逐步增加采样次数的方法来获得稳定的结果。其收敛规则为：设定采样轨迹的最低条数(Nmin)与最高条数(Nmax)。首先采样Nmin条轨迹，然后逐次新增采样固定条数(设为M)的轨迹，将新增的M条轨迹加入所得轨迹集C中。当出现以下情况之一时，采样结束：一是当逐次新增采样的过程中所产生的最优路径集ZK连续若干次(设为H次)一致时，结束采样；二是采样轨迹总数(记为Q(C))达到最高条数Nmax，结束采样。最优路径集计算的具体步骤如下：

Step 1：令采样轨迹集C=∅；用t表示新增采样过程中，所得轨迹集C中出现频率排名前K位的路径连续一致的次数，初始时令t=0。

Step 2：按照轨迹采样方法采样Nmin条轨迹，记Nmin条轨迹集为CNmin，令C=CNmin；统计轨迹集C中出现频率排名前K位的路径，得到路径集ZK。

Step 3：按照轨迹采样方法新增采样M条轨迹，将新增的M条轨迹加入轨迹集C中；统计轨迹集C中出现频率排名前K位的路径，得到路径集Z′K。

Step 4：判断Q(C)≥Nmax是否成立。若成立，则更新ZK=Z′K,采样结束；否则，进入Step 5。

Step 5：判断轨迹集C中出现频率排名前K位的路径集是否有变化。如果有变化(即Z′K≠ZK)，令t=0并更新ZK=Z′K，返回Step 3；否则，令t=t+1，进入Step 6。

Step 6：判断t≥H是否成立。若成立，采样结束；否则，返回Step 3。

采样结束后，所得到的路径集ZK即为最终的最优路径集。

2 案例分析

为验证本文方法，选取广州市越秀区的一对起点r与终点s为例子，采用的数据为2014.02.24—03.21约1个月的广州市出租车历史出行轨迹。一方面，案例选取出租车的历史轨迹数据，是由于出租车轨迹数据包含了真实的出行路径，可用于对计算产生的路径进行检验。另一方面，选取该实验区域是由于该区域内部之间具有足够多的历史出行轨迹。

根据交通出行特征的相似性，对区域进行划分，记起点r、终点s所在区域分别为区域O、D。为分析区域划分大小的影响，将该路网范围按2种不同的网格大小进行划分(分别称为“粗划分”与“细划分”)[8]。粗划分情形下单个区域较大，可获得更多历史出行数据；细化分情形下单个区域较小，可更体现出行特征。2种种划分情形如图3所示。

图3 交通小区划分

根据广州市交通状态随时间的变化，选取早高峰(7:00～9:00)、晚高峰(17:00～19:00)、平峰(12:00～14:00)共3个时段，并与粗划分、细划分2种区域划分情形进行组合，从而得到6种组合进行实验。

从历史轨迹中选取给定时段下、由区域O前往区域D的轨迹，作为有效轨迹集ΓOD。

由起点r选择每个起始路段al(l{1,2,…,IA})的概率计算如下：

(3)

路段ai到路段aj(i,j{1,2,…,IA}，i≠j)的转移概率计算如下：

(4)

考虑出行者需求一般为2～3条参考路径，根据最优路径集计算方法，本案例取K=3；为验证方法的合理性，此处设定较严格的收敛条件，取H=5。下面通过初步试验来设定Nmin、Nmax、M的值。

Nmin的设定需根据K值而变化，当K值更大时，Nmin也需设定更大的值。根据试验经验，Nmin大约取K值的15～20倍。经过试验，当采样轨迹总数达到40～60条时，出现频率排名前二的路径有较稳定的结果，而出现频率排名第三的路径在数条路径间变动，因此，本案例取最低采样条数Nmin=50。为避免因特殊情况导致采样结果难以收敛，本案例取最高采样条数Nmax=500。

对于每次新增采样条数的设定，取M=10,20,30作试验。结果显示：M=10时，所需轨迹采样总数虽然相对较小，但不能很好地确保采样的收敛性，在某些实验中出现频率排名第三的路径难以稳定；M=20时，可在较低的轨迹采样总数下达到收敛，同时可基本保证采样的收敛性；M=30时，采样轨迹总数会较大幅度增加，明显降低计算效率。因此，本案例取M=20。

2.1 收敛性分析

该案例实验在配置为Intel(R) Pentium(R) CPU G640、Windows 7的平台上使用Matlab软件来运行，共进行了6次实验(表1)，每次实验平均所需运行时间仅约0.59 s，对计算机性能要求较低。由每次实验达到收敛时所需的采样轨迹总数(表1)可知：每组实验达到收敛时所需的采样轨迹总数约为150～300条，平均所需采样轨迹总数约为200条，即在设定的最低采样轨迹数的基础上，新增采样次数平均约为7次，表明算法收敛性良好。

表1 收敛时所需新增采样次数及采样轨迹总数

由于本研究采用概率采样方法，收敛时所需新增采样次数和采样轨迹总数只与转移概率的分布有关，区域划分大小和不同时段对概率分布影响不大，因此，所需新增采样次数和采样轨迹总数在不同条件下基本一致。其中细划分情况下所需新增采样次数及采样轨迹总数略低于粗划分情况下的，原因是细划分情况所获取的有效轨迹相对于特定的起终点更加精确，因此，计算路径略快地收敛于验证路径。

2.2 准确性分析

将每次实验所得出现频率排名前三的计算路径与选择频率(某条路径的选择次数占实际出行轨迹总数的比例)排名前三的验证路径进行整理，合并两者重复出现的路径，从而得到6条不同的路径;由于实验所产生的计算路径与验证路径有部分路段重叠，为了在一张图中直观描绘，将不同路径之间存在分支的交叉口处用黑色节点加以表示；对于一条完整的计算路径或验证路径，用该路径依次经过的节点来表示(图4)。表2给出了每次实验所得出现频率排名前三的计算路径与选择频率排名前三的验证路径的对比。

图4 高频率出行路径

实验结果(图4、表2)表明利用最优路径集路段转移概率法所产生的计算路径与验证路径之间的覆盖程度较高：(1)每次实验中出现频率排名前二的计算路径与选择频率排名前二的验证路径均一致；实验III和实验IV中出现频率排名前三的计算路径与相应的验证路径完全一致，其他实验中仅频率排名第三的计算路径与相应的验证路径不同，表明最优路径集路段转移概率法的有效性。(2)每次实验中出现频率排名前二的计算路径的出现频率较大，同样条件下的选择频率排名前二的路径的选择频率也较大，表明计算路径与实际的选择路径可准确覆盖；而代表其他路径的轨迹的数量所占比例均较小，不能准确计算，因而计算结果产生差异。另外，根据计算所得路径的完整排名结果及对应的实际数据统计的路径完整排名结果，实验II、V、VI中，出现频率排名第三的计算路径在相应的验证路径中选择频率排序第四，由于本文提出的方法为基于历史数据的估算，产生路径的排序有差别属正常结果；实验I中出现频率排列第三的计算路径在其对应的验证路径中排序靠后，原因是该次实验的验证轨迹数量较少，除了出现频率排名前二的计算路径之外，代表其他路径的轨迹数量很少且彼此之间相差小于3条，导致计算结果的偶然性。

不同条件下的对比结果(表2)表明：(1)区域划分大小对计算结果的准确性影响较小。在粗划分(实验I、II、III)与细划分(实验IV、V、VI)各3次实验中：均有1次实验的排名前三的计算路径与验证路径完全一致；在其他实验中排名前二的2条路径保持一致，仅排名第三的路径不一致。由于点对数量巨大，特定起点和终点很难采集足够数据进行分析，案例结果表明用出行区域替代具体起终点是可行的，可明显降低对数据的要求，增强方法的实用性。(2)不同时段下的计算路径存在差异性。在粗划分的3个不同时段(实验I、II、III)中，平峰时段与其他2个时段条件下所得出现频率排名第三的计算路径和选择频率排名第三的验证路径不一致；在细划分的3种不同时段(实验IV、V、VI)中，晚高峰与平峰时段所得出现频率排名第三的计算路径和对应的选择频率排名第三的验证路径均不一致。并且，早高峰与其他时段条件下的出现频率排名前二的计算路径和选择频率排名前二的验证路径排序均不同。该结果表明对时段进行划分是有必要的，可有效反应交通状况的影响。

表2 高出现频率的计算路径与高选择频率的验证路径

3 结论

车辆在交叉口的转向数据是很容易获取的数据，且隐含出行者对路径的选择。由于出行者往往需要在多条备选路径中进行选择，本文利用转向数据，提出基于路段转移采样来获取多条最优路径的方法(最优路径集路段转移概率法)。该方法不需计算路段阻抗，考虑了交通状况随时间变化的影响，利用出行区域替代特定的起点和终点来避免历史数据量不足的问题。采用广州市越秀区某对起点和终点的出租车数据，在早高峰、晚高峰和平峰3个时间段的验证结果表明：最优路径集路段转移概率法的计算路径与实际验证路径的涵盖程度高，对数据要求低，可通过扩展出行区域范围来获取更充足的数据量，对时段进行划分可有效反应交通状况。

本研究所采用的数据较为齐全，但在实际工程中可能遇到数据难以覆盖研究区域内所有路段的情况，未来可以针对部分路段数据缺失的情况进行拓展研究。另外，本研究中交通小区的划分方式较简单，利用历史数据对交通小区进行智能划分来提升结果精度也值得进一步研究。