基于PCA-ERBF-SVM的边坡稳定性分析模型*
姚 怡, 王晓敏
(西安科技大学 高新学院,陕西 西安 710109)
本世纪以来,全球科技发展突飞猛进,与此同时各种工程活动也在不断加剧,水利工程建设活动便成为了全社会重点关注的对象[1-2]。而随着水利工程建设过程中所涉及的技术水平越来越先进,对工程地质环境的破坏越来越严重,尤其是工程开发区域的边坡稳定性成为了工程建设者和相关研究人员关注的焦点[3-4]。
从20世纪开始,学者们就已经逐步开展了对坡体稳定性的研究[5]。最初,人们将结构面相关理论引入到边坡稳定性研究中,就此形成了岩体结构的雏形[6]。20世纪70年代开始逐渐转向对边坡变形的机理及失稳过程的研究[7]。直至21世纪初以来,随着计算机技术和通信技术的发展,研究方法开始从传统的定性研究向现代的定量研究转变[8-9]。
近年来,有学者采用快速拉格朗日有限差分法对岩体变形的过程进行数值模拟建立本构方程[10],该方法虽然可运用于对各类材料,但其过程繁琐计算复杂,实际并未得到广泛应用;有研究人员利用Morgenstern-price极限平衡法针对尾矿坝边坡进行稳定性计算[11],但该方法本身需要假设破坏面,过于依赖经验;也有研究者借助神经网络构建边坡稳定性分析模型[12],但这种方法需要大量的工程数据且神经网络本身具有不可避免的缺陷,如“黑匣子”问题等,这就造成当预测失败时很难针对原因进行改进;有研究者基于因子分析和模糊理论对边坡稳定性进行研究[13],该方法有效解决了神经网络的不可解释性,同时也在一定程度上避免了对于经验的依赖,但求解权重的过程难以找到最优途径;还有研究人员将网格搜索SVM应用于边坡稳定性分析[14],尽管取得了一定的效果,但网格搜索过于耗时,不适合参数过多的情况。
为了改善以上研究方法的缺点,同时,考虑到影响边坡稳定性的各因子之间可能具有相关性,这种相关性可能会使输入变得复杂且影响分析效果,因此研究中采用主成分分析PCA结合扩展RBF核支持向量机建立边坡稳定性分析模型,并通过免疫算法对模型参数进行优化,以提高边坡稳定性的预测精度并缩短模型的训练时间。
1 研究区概况
1.1 气象水文
崆峒水库建于甘肃省平凉市西部的中山区和泾河峡谷内,距平凉市区约12 km[15]。泾河源于六盘山,经大阴山后到达崆峒山,位居黄河中游,是渭河主要支流之一,该流域所属为半湿润半干旱气候带。降水主要集中于第三季度,年均降雨量约680 mm,几乎占到该区域全年降雨总量的70%。水源主要来源于雨水,暴雨成为径流的重要补给方式。径流变差系数为0.5左右,其年际变化较大。
1.2 地形地貌
崆峒水库是平凉市西部唯一具有调蓄能力的水库,属于不完全年调节水库,目前以服务地方农业为主,兼顾市区生活和发电站供水[16]。该水库类型为峡谷型,河流由南向北蔓延,谷底状似V字型,两侧距离30~90 m,河床两侧距离10~25 m,河道两岸地势陡峭。崆峒水库的西面是崆峒主峰,边坡与河道近似呈90°夹角;水库东面地势略微平缓,边坡坡角大约为30°~50°,水库两侧山坡的相对高差为400~500 m。
1.3 水库容量
水库控制积水面积约602 km2,多年平均流量为3.59 m3/s,多年平均径流量1.13×108m3。崆峒水库总容量为2.97×107m3,死库容量为6×106m3,有效库容量为2.23×107m3,改扩建工程将库容提升至4.57×107m3。
2 基础理论
2.1 RBF核SVM
SVM的基本想法是在样本空间中构造最优超平面,满足该平面与样本间的距离最大化,从而使其泛化能力得到增强[17]。图1所示为SVM示意图。

图1 支持向量机
SVM以分类间隔最大化为主要目标,目前已发展为一种优越的回归预测方法[18]。设系统输入为n维(n>1),输出为1维,样本集T={(x1,y1),…,(xi,yi),…(xl,yl)},其中xi∈Rn为输入变量,yi∈R为输出变量,i=1,2,…,l。以f(x)=ω·x+b为例,允许拟合存在误差的情况下,选用ε误差不敏感函数,则软间隔SVM可表述为:
minω,b,ξ(*)
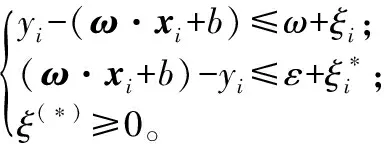
(1)
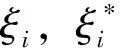
2.1.1ν-SVM
由于ε难以预先指定,由传统SVM发展来的ν-SVM有效地避免了这一问题[19]。其描述为:
minω,b,ξ(*),ε
(2)
式中:v∈(0,1]用于控制支持向量数量。采用拉格朗日乘子,可得上述问题的对偶问题:
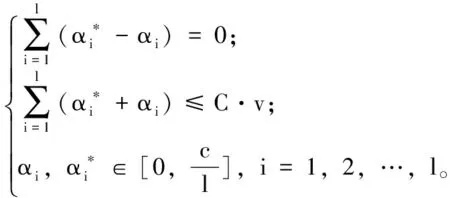
(3)
求解上式可得(α,α*),对新的输入变量x构造线性回归预测函数:
(4)

(5)
由于边坡稳定分析模型非线性的特点,因此样本T几乎无法位于超平面上,所以将输入变量x映射至高维空间Φ(x)。回归预测函数可表示为:
(6)
对于一般的多输入变量问题,由映射到的映射几乎无法预先指定,故引入核函数K(xi,x)=(Φ(xi)·Φ(x))。当前常用核函数有Sigmoid核函数、径向基核函数、多项式核函数等[20]。
2.1.2 ERBF-SVM
正是因为径向基核函数拥有极强的逼近能力,现已被用于各种工程领域当中。当输入变量x为d维时,RBF核形式如下:
K(x,x′)=exp(-(x-x′)TQ(x-x′))。
(7)
上式说明计算RBF核时各输入变量的分量被赋予同样的权值。而实际工程问题中显然无法满足以上条件,当输出受多因子影响时,各因素对结果的贡献是不一致的。为此,这里考虑对角矩阵Q为对称正定阵的情况,可以证明,此时由式(7)确定的K(x,x′)仍然可以成为一个核函数。
研究中考虑Q为正定对角阵,其主对角元素qii>0,i=1,2,…,d为核函数参数,可通过2.2节的优化方式确定。以扩展RBF为核函数的支持向量机记为ERBF-SVM。
2.2 参数优化
为了训练ERBF-SVM,需确定的参数包括C、v和qii。为了寻找最合理的参数组合Ab,结合免疫算法,以待定参数(C,v,q11,…,qdd)为抗体,以最终值为抗原,抗体可以自适应学习抗原,具体流程如图2所示。
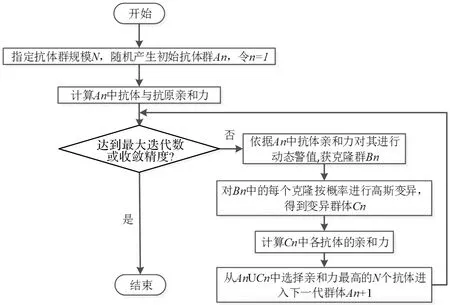
图2 免疫算法流程图
2.2.1 亲和力
设样本集T中含有l个样本,将其按照(l-1)∶1的比例划分为训练集和验证集,假定误差为ei,则
(8)
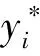
(9)
抗体Ab的亲和力为:
(10)
2.2.2 动态繁殖算子
已知抗体亲和力和抗体间距离的前提下,为了确定抗体繁殖数量,引入动态繁殖算子。再在该算子中引入δ(抑制半径)、pr(抑制概率),具有较高亲和力的Ab可以有效抑制具有较低亲和力的Ab,被抑制的Ab就无法进行繁殖。算法的具体流程如图3所示。

图3 优化算法流程图
抗体的抑制范围取决于的大小,也就是说,δ与抗体间最大距离相关。
δ=η×maxi,j=1,…,n(d(Abi,Abj))。
(11)
这里,d(Abi,Abj)表示Abi到Abj的Euclid距离。
(12)
这里,iter表示当前迭代次数,表示最大迭代次数。
3 模型建立
结合基础理论,建立了基于PCA-ERBF-SVM的边坡稳定性分析模型如(图4)。模型建立步骤如下。
步骤1:选取边坡失稳的致灾因子数据集;
步骤2:对Step1中所选数据进行归一化[21]处理;
步骤3:对归一化处理后的数据进行PCA分析,从初始影响因子中提取出主要影响因子;
步骤4:将Step3中选取的因子数据随机划分为训练样本、预测样本和验证样本,以Step3的结果为输入,稳定性系数为输出建立PCA-ERBF-SVM模型;
步骤5:利用遗传算法对模型进行优化,确定参数;
步骤6:利用预测样本的数据对经Step5后训练好的模型进行预测;
步骤7:利用验证样本数据对模型进行验证并对结果作出分析。
4 算例分析
SVM的计算速度由输入数据的维度所决定,因各因子之间存在相关性,所以借助PCA来筛选出不相关的主成分并将其剔掉,使得所建模型的分析效果得以提升。
4.1 主成分提取
此处选取边坡稳定性分析中常用的6个影响因子[22]构成模型输入矩阵,具体参数及符号表示如表1所示。
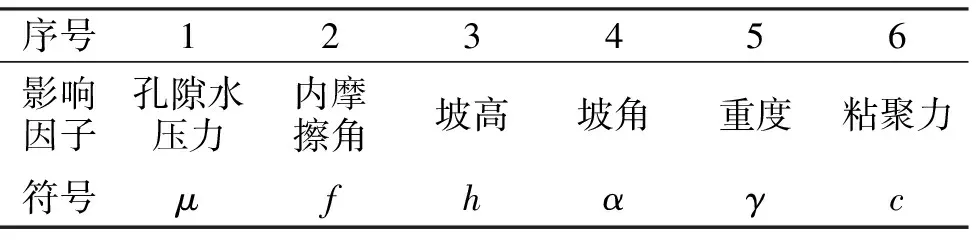
表1 影响因子符号表示
以前文所述工程为例,随机选取200组数据作为算例分析的样本集,并按照180∶15∶5的比例将样本集划分为训练集、预测集和验证集。其中,预测样本数据和验证样本数据如表2和表3所示。

图4 模型建立流程
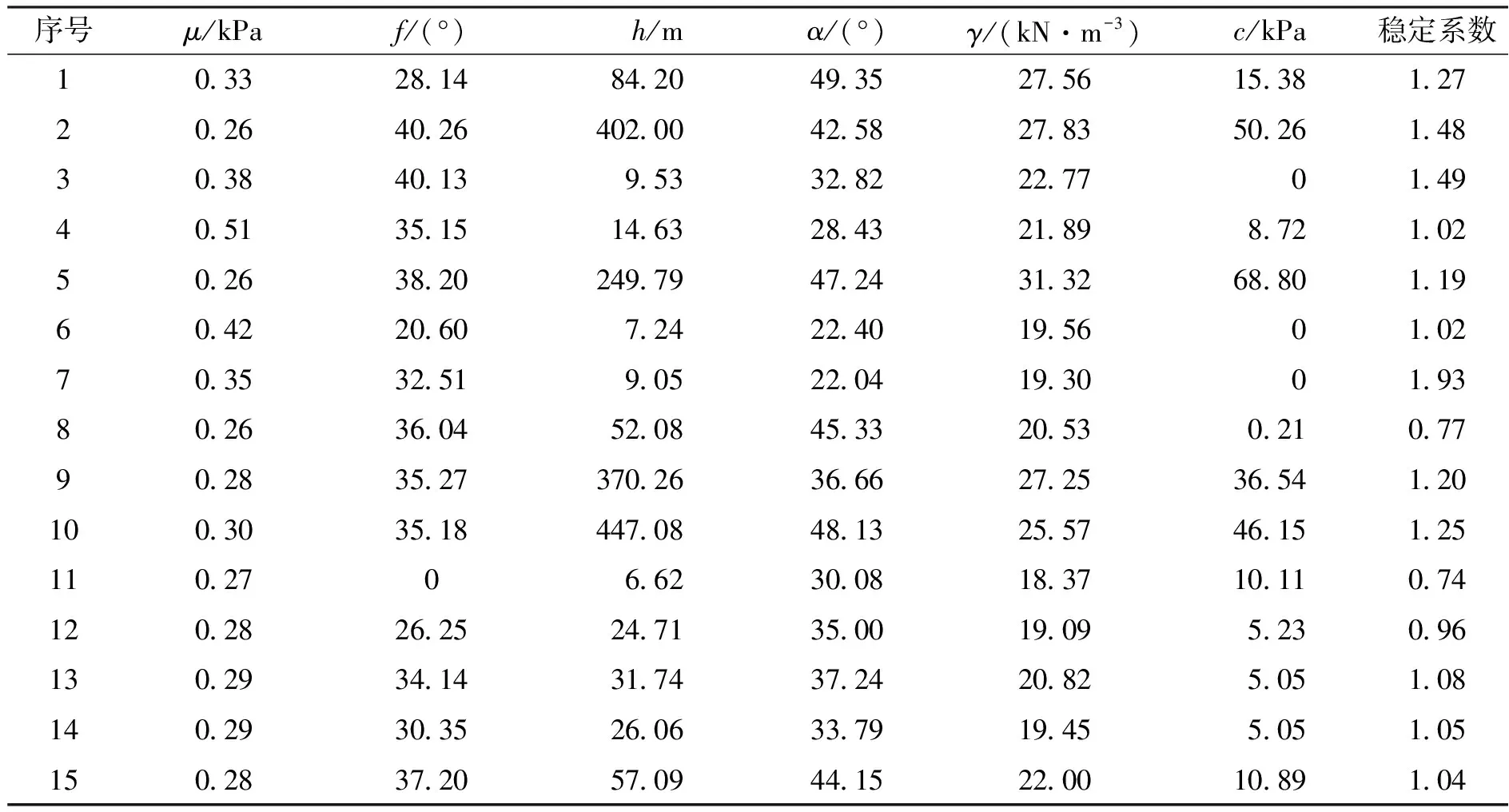
表2 预测样本集

表3 验证样本集
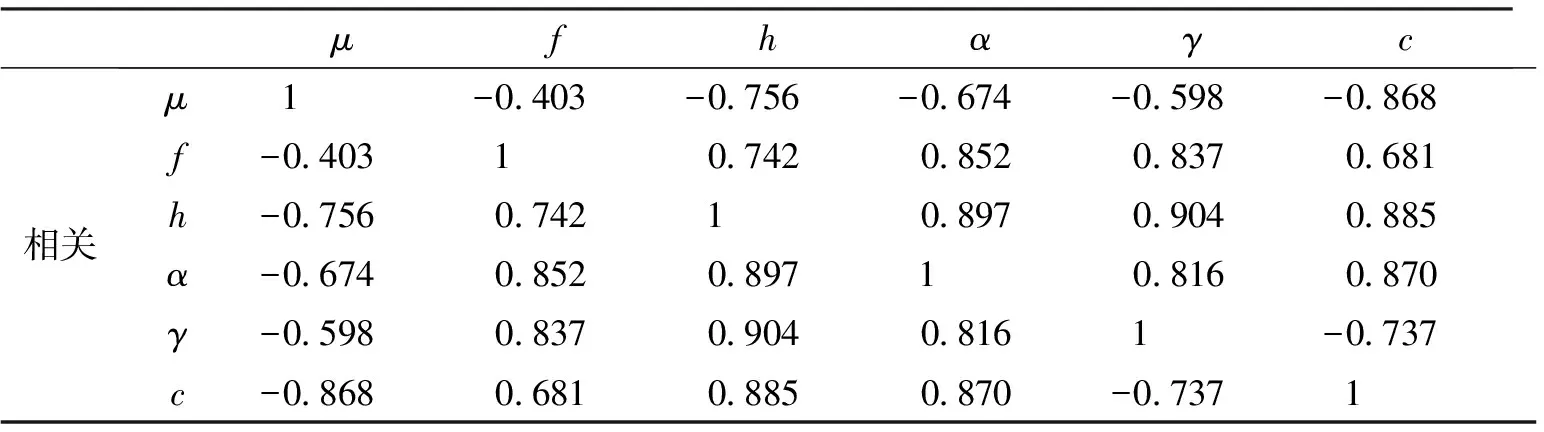
表4 相关系数矩阵
对表2中的各因子数据做相关性分析,得到相关系数矩阵,如表4所示。
从表4可以看出,因子之间相关性在0.8以上的有8个,根据PCA原理[25]可以判断,这些因子间存在一定相关性。如果以以上6个因子作为模型输入,输出的准确度势必会收到影响,为了保证结果的准确性,需要对输入数据的主成分进行分析。
通过SPSS软件对预测样本集中的输入数据进行分析,得到成分矩阵如表5所示,方差如表6所示。
表6数据显示,第一个主成分的贡献率达83.571%,第二个主成分的贡献率为12.905%,这两个的累计贡献率已占到总贡献率的96.476%,可以有效反应出输入数据的信息。

表5 成分矩阵
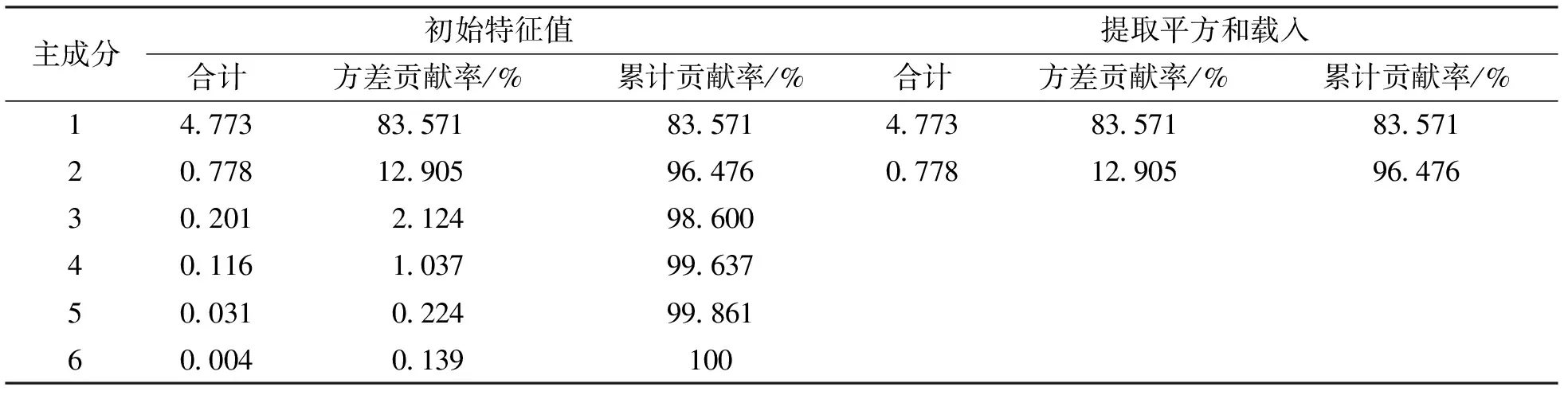
表6 解释的总方差

表7 主成分因子载荷数据
再将表5中的数据通过Transform-computer变换,得到主成分载荷因子矩阵,如表7所示。
根据表7数据,写出主成分表达式,如式(13)所示。
(13)
4.2 仿真实验
采用传统SVM进行边坡安全计算时,由于输入变量之间可能具有相关性且输入数据维数过大,因此结合PCA与SVM构建模型并利用免疫算法进优化,以期对边坡稳定性系数做出合理的分析。
根据边坡模型的特点,选用ERBF核函数作为支持向量核函数,需要调整的参数共有4个:C、v、q11、q22。其中,0.001≤C≤1 000,0.001≤v≤1,0.001≤qii≤1,i=1,2。为了找到最优的4个参数,采用前文所述的免疫算法进行寻优,具体设置如表8所示。

表8 免疫算法参数设置
利用前文选取的180组数据分别对经PCA处理后的PCA-ERBF-SVM模型和未经PCA处理的ERBF-SVM模型进行训练,采用预测样本集中的15个数据对边坡稳定系数进行预测,将两种模型预测结果进行对比,如图5所示。
图5中实际值为采用圆弧滑动法计算所得,后文与此一致。从图5可以看出,PCA-ERBF-SVM的预测结果更接近实际边坡稳定性系数。显然,预测效果比ERBF-SVM更好,说明采用PCA对输入数据进行降维是很有必要的。
再依次选取训练样本集中的10组数据、20组数据、…、180组训练数据,将PCA-ERBF-SVM的预测结果与目前研究中常见GA-BP神经网络[23]进行比较,GA-BP的参数设置如表9所示,误差如图6所示,稳定性预测结果如图7所示。

表9 GA-BP参数设置
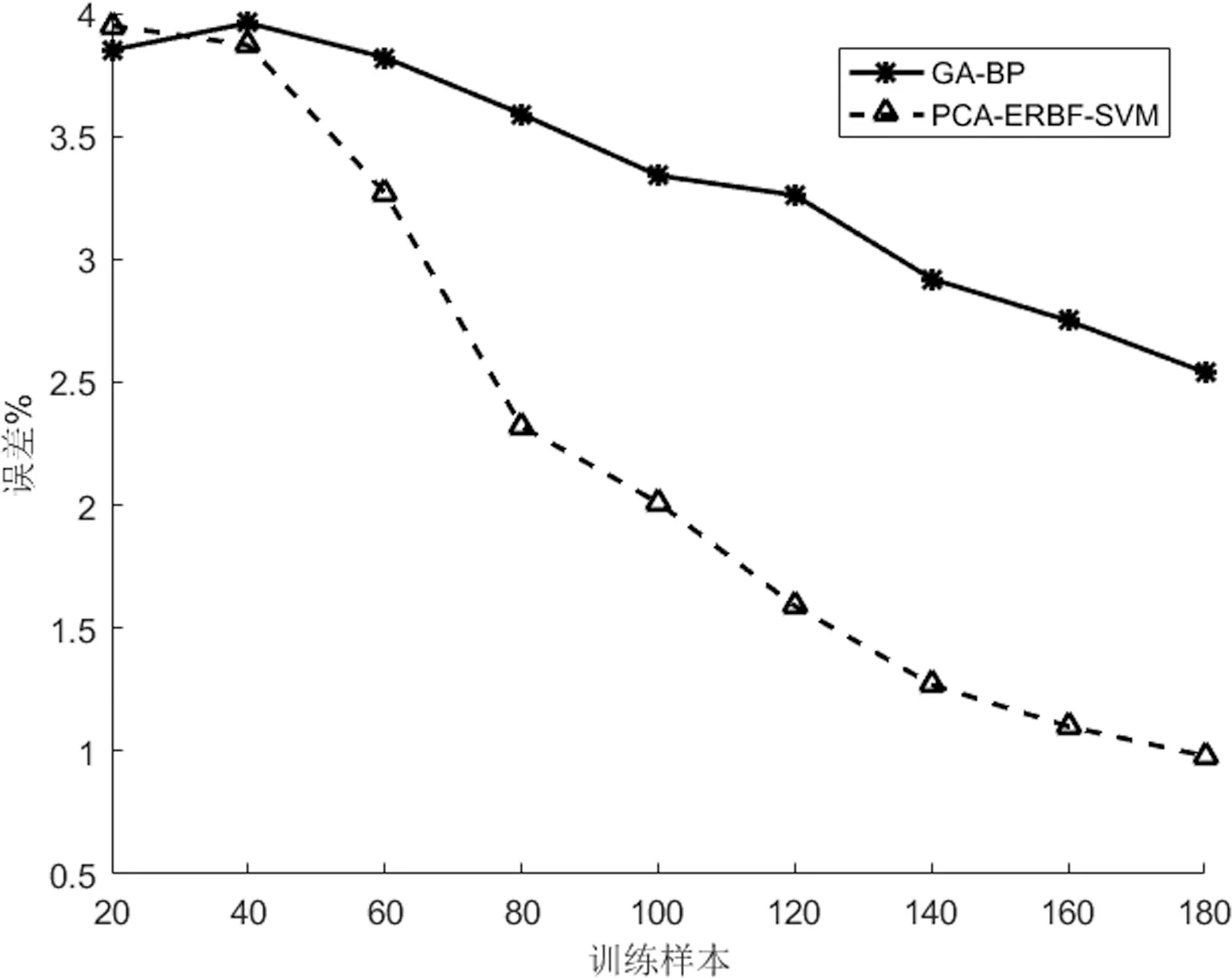
图6 不同训练样本数误差对比

图7 不同训练样本稳定系数对比
图6中,PCV-ERBF-SVM表示PSV-ERBF-SVM的误差曲线,GA-BP表示GA-BP神经网络的误差曲线。可以看出,当训练样本数据较少时,二者的误差均较大,随着样本的增加误差均逐渐减小。但是当样本数达到180个时,PSV-ERBF-SVM的误差已经降至0.001以下,而GA-BP的误差在0.01以上。这说明PSV-ERBF-SVM在处理小样本集时更具优势。
图7中,PSV-ERBF-SVM-50、PSV-ERBF-SVM-100、PSV-ERBF-SVM-180分别表示样本为50个、100个、180个时PSV-ERBF-SVM的预测结果,GA-BP-50、GA-BP-100、GA-BP-180分别表示样本数为50个、100个、180个时GA-BP神经网络的预测结果。从整体上看,样本数越多,PSV-ERBF-SVM的预测值越接近于实际值,而GA-BP的趋势则表现的不明显,这也与样本数较少有关,再次说明PSV-ERBF-SVM更适合小样本集的数据处理。同时,PSV-ERBF-SVM-180的预测结果与实际值已非常接近,说明将PSV-ERBF-SVM模型用于边坡稳定性分析是有可能的。
为了进一步分析该模型的有效性,用同样的数据分别训练传统的网格搜索SVM模型(PCA-SVM)、一般RBF核SVM[24](PCA-v-SVM)、多尺度SVM[25](PCA-MS-SVM),分别以均方根误差RMSE[26]、LOO误差和训练时间TIME为指标与扩展RBF核SVM(PCA-EBRF-SVM)的结果进行比较,如图8和表10所示。
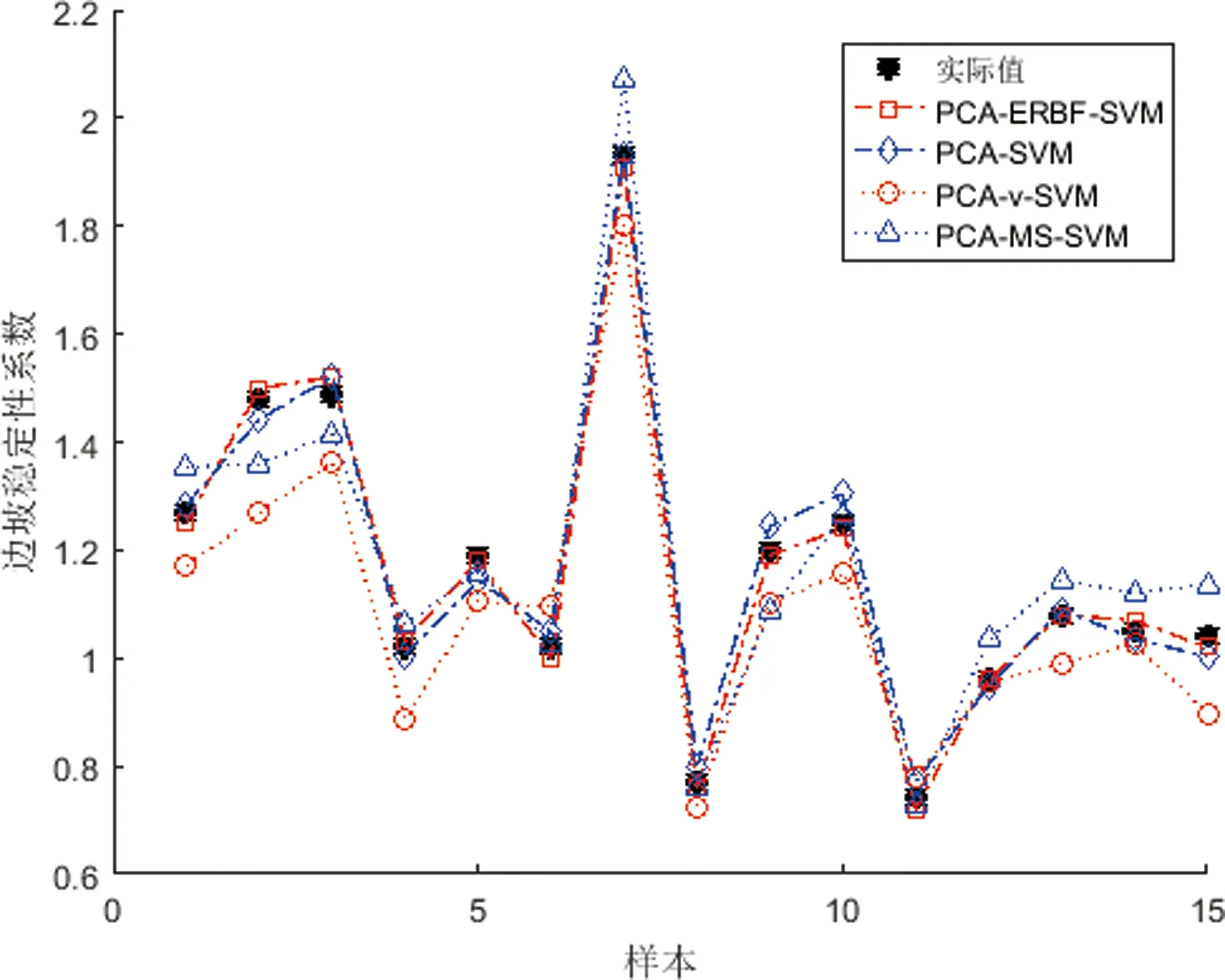
图8 四种模型的预测效果
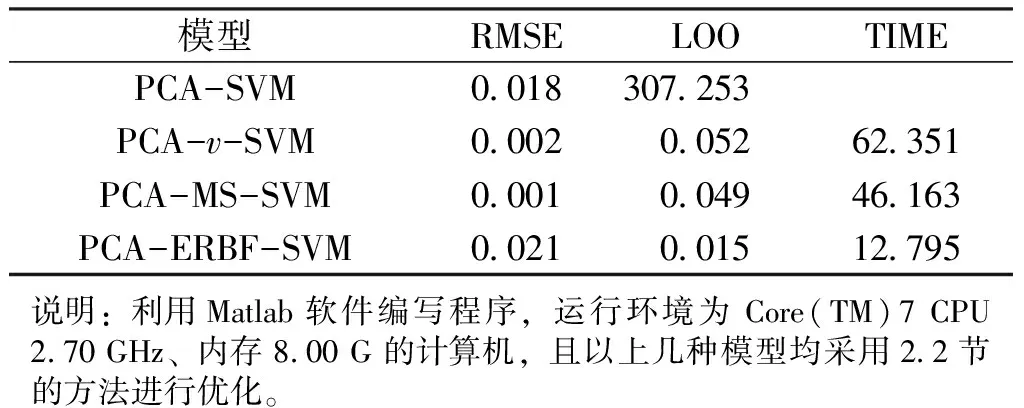
表10 四种模型的指标评价
从图8可以大致看出,整体上PCA-ERBF-SVM和PCA-SVM的预测结果都十分接近实际值,在个别样本点处,PCA-SVM的表现甚至更优于PCA-ERBF-SVM。PCA-MS-SVM的预测效果较弱,而PCA-v-SVM的预测值偏离实际值最远。
表10数据表明,从误差来看,PCA-EBRF-SVM和PCA-SVM的性能十分接近,PCA-ERBF-SVM并没有表现出明显的优势,但从训练时间来看,PCA-ERBF-SVM仅是PCA-SVM的4.16%,优势相当明显。随着实际工程中所采集的数据越来越多,PCA-EBRF-SVM的优势将更加明显。
利用表3中所列的崆峒水库五个测试点处的边坡影响因子数据再次对PCA-ERBF-SVM模型的有效性进行验证,分别与PCA-v-SVM模型、PCA-MS-SVM模型和PCA-ERBF-SVM模型进行比较,边坡稳定性系数如图9所示,绝对误差如表11所示。

图9 四种模型在不同测试点处的边坡稳定性系数

表11 四种模型在不同测试点处的误差
图8曲线表明,PCA-ERBF-SVM在五个测试点处的结果最接近实际值,从表11可以看出,PCA-ERBF-SVM在五个测试点处的绝对误差和LOO误差均为所有模型中最小的。图9和表11的结果再次验证了PCA-ERBF-SVM在边坡稳定性分析中的有效性。
5 结论
(1)本研究将PCA和扩展RBF核的支持向量机相结合构建PCA-ERBF-SVM边坡稳定性分析模型,并通过免疫算法对模型中的参数进行了优化。首先通过PCA对输入矩阵进行简化,很大程度上减小了因影响因子间存在相关性所引起的计算误差,然后利用化简后的数据对边坡稳定性进行预测,实验结果证实了该方法的有效性。
(2)PCA-ERBF-SVM模型输出的边坡稳定性系数与RBF-SVM模型输出的边坡稳定性系数表明,经PCA处理后的预测准确率更高,误差更小,表明将PCA算法对边坡稳定性影响因子作用的有效性。
(3)PCA-ERBF-SVM模型与常用的GA-BP模型、PCA-SVM模型、PCA-v-SVM模型和PCA-MS—SVM模型分别进行对比,结果表明PCA-ERBF-SVM模型的输出结果与实际值最接近,同时均方根误差、LOO误差和训练时间也最小,研究区的验证结果再次验证了该模型的有效性和可行性。
(4)考虑到研究中所用工程数据的局限性,该模型的普适性还有待进一步验证,后期还需通过更多的边坡数据类型和样本量对其普适性加以验证。

