基于一致性算法的城市微网群分层协同控制
刘鑫蕊,张明超,王 睿,孙秋野
(东北大学信息科学与工程学院,辽宁省沈阳市 110819)
0 引言
微网(microgrid,MG)由风电机组和光伏等分布式电源、蓄电池、负载和其他发用电设备组成[1]。单一微网的供电质量和稳定性较差[2],当分布式电源或负载的功率波动时,可能会破坏整个微网的稳定性[3],故延伸出微网群(microgrid cluster,MGC)的概念。通过适当的控制策略,可使能量在各子网之间有序流动[4],从而提高系统的稳定性和供电质量[5]。由于城市内各微网间地理距离较小,且负荷分布密集、负荷投切较频繁,建设城市微网群供电系统可充分利用微网间信息传递、能量互济互补和降碳环保,具有较好的现实意义。
现有微网控制策略多为分层控制[6]。文献[7]提出一种基于一致性算法的分布式储能系统功率分配策略,但未讨论储能系统间的功率传输损耗,无法应用于微网群。结合优化算法的集中式分层控制被广泛应用于微网群,顶层为能量管理层,负责制定微网群的运行策略;中间层用于选择微网的运行模态;底层为设备层,负责实现对微网内部各控制器的控制[8-11]。文献[12]提出直流微网群各子网分散自律控制方案,但未针对储能设备荷电状态(state of charge,SOC)不足或过高引起子网工作状态的切换给出解决方案,而这种工作状态的切换会破坏整个多微网系统的稳定性。
近年来,分布式控制架构[13]和多智能体一致性算法被广泛应用于交直流混合微网群控制[14]、优化调度运行[15]、功率分配[16]、多微网协调控制[17]、多光伏分布式协调控制等领域[18]。与集中控制相比,基于一致性算法的微网群分布式控制降低了对通信系统的要求[19]。文献[20]提出一种基于一致性算法、以经济性为目标的微网群分层控制策略,但在上层功率分配过程中未考虑蓄电池SOC 变化导致工作模式的切换,仅将其作为约束条件进行优化,影响了系统的稳定性和经济性。文献[21]提出一种基于一致性算法的功率分配策略,优化了微网群的运行成本,但未讨论蓄电池的SOC 差异给微网群带来的影响。文献[22]提出一种针对互联微网的分层能源管理策略,虽然微网群系统能够在进行功率分配的同时降低微网群的运行成本,但中央能源管理系统将增加微网群对通信系统的要求。
为解决蓄电池SOC 变化导致城市微网群工作模式的频繁切换,本文提出基于一致性算法的城市微网群分层控制方法。顶层控制通过一致性算法获得微网群蓄电池组负载率;底层控制由各子网根据蓄电池SOC 和蓄电池组的负载率求解并控制其各可控单元的功率。该方法具有以下三方面优势。
1)顶层控制减少了由于SOC 偏离正常工作区间而导致工作模式的切换,进而降低了微网群系统的调节成本。
2)能量在子网间有序流动,避免了其在蓄电池间的环流。
3)各可控单元根据顶层控制制定的优先级次序依次求解并控制其功率,降低了成本。
1 微网群多智能体的一致性算法
1.1 微网群的结构
微网群是由互联的分布式中压或者低压微网组成的具有特定功能和运行目标的系统。微网群中的各子网不仅需要独立运行,还需要接收和执行微网群的调度指令,完成群级运行目标。每个微网可以通过群级命令与其他微网实现能量互济。根据运行方式的不同,微网群可以分为并网运行微网群和孤岛运行微网群。为体现近零碳微网群系统的风光储互补特性,本文所构建微网群中分布式电源仅考虑风电和光伏。在孤岛运行模式下,直流微网群的拓扑及其分布式通信控制结构如图1 所示。不失一般性,本文假设子网、智能体、节点和蓄电池的序号是一一对应的。

图1 微网群结构Fig.1 Structure of microgrid cluster
1.2 多智能体一致性算法的数学模型
多智能体可用图G={Q,E}表示,其中,Q表示微网群中相互独立的智能体集合;E⊆Q×Q是一组边,从节点i到j的无向边由无序对(i,j)∈E表示,节 点i的 邻 集 表 示 为Ni={j|j⊆Q;(i,j)∈E}。图G的邻接矩阵A=(aij)表示节点间的通信关系,若节点i和j存在通信链路,则aij=1,否则aij=0,且所有对角线元素aii=0。
每个智能体状态的变化取决于其自身的当前状态以及与其在通信结构上相邻智能体的当前状态。在计算功率时,通过引入收敛系数γ将微网间功率传输损耗代入一致性迭代公式,进而提高一致性算法的收敛精度,可得:
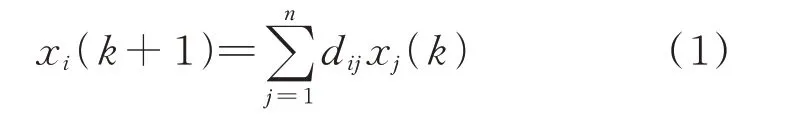

式中:xi(k)和xj(k)分别为第i个节点状态变量和第j个节点状态变量第k次迭代值,i∈Q,j∈Q;yi(k+1)为引入收敛系数后的第j个节点状态变量第k次迭代值;dij为第i个节点和第j个节点智能体之间的通信系数;γj为第j个节点状态变量的收敛系数;n为智能体总数。
在多智能体网络中,每个智能体与相邻的智能体基于状态转移矩阵D完成迭代更新。为了实现算法的高效和准确,通信系数dij构造如式(3)所示。当D为双向随机矩阵时,每个节点i的稳定状态变量xi,∞通过一致性算法收敛到初始状态变量的平均值,如式(4)所示[23]。
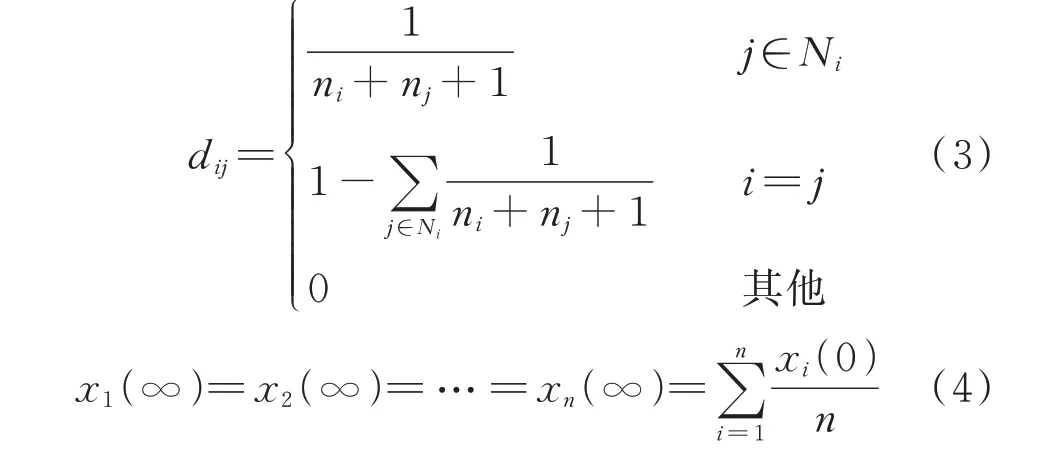
式中:ni为节点i邻接点的个数;xi(0)为第i个节点状态变量的初始值;xi(∞)为第i个节点状态变量迭代后的收敛值。
本文所提功率分配策略的控制输入是蓄电池的功率,状态变量是蓄电池的SOC。关于一致性算法收敛性的证明见附录A[24]。在城市微网群分布式控制架构下,运行数据在子网间传输的通信时滞较小,这为一致性算法应用于微网群并且实现收敛提供了通信保障。
2 微网群的分层控制
本文根据控制目标不同分为顶层控制和底层控制。顶层控制首先根据SOC 求出蓄电池单位调节成本和可中断源荷切除的单位成本用来制定各可控单元的调节优先级,然后,基于一致性算法得出蓄电池负载率;底层控制根据顶层求得的蓄电池负载率、各可控单元的调节优先级和子网内各蓄电池SOC校正值,为各可控单元分配功率并执行功率命令。算法流程如附录B 图B1 所示。
2.1 微网群的顶层控制
2.1.1 基于调节成本的可控单元调节优先级制定
微网群的运行成本包括微网中各可控单元的功率调节成本和各微网之间能量传输损耗成本。微网群中可控单元的调节成本可以用采样间隔TS内调节的电量来计算。
为有效延长蓄电池的工作寿命并避免其频繁地深度充放电,为蓄电池SOC 设置这2 个边界值,其中,Smax为 上 界 值;Smin为 下 界 值。当SOC 在2 个 边界值划定的区间外时,蓄电池退出运行。在此基础上,定义2 个SOC 预警值,其中,Shigh是上预警值;Slow是下预警值。4 个边界预警值将SOC 运行区间分为3 段,如附录B 图B2 所示。通过在不同的SOC区间段设定不同的蓄电池调节单价(SOC 区间段距离上、下边界越近,调节单价越高)来降低SOC 到达临界状态的速度,进而起到减少微网群工作状态切换次数和降低微网群运行成本的作用。蓄电池的功率调节成本如下式所示:

式中:CDG,i(∙)为第i个子网采样区间内分布式电源的切除成本;rDG,i为分布式电源的单位调节电价;ΔPDG,i为分布式电源的切除功率;PmaxDG,i为分布式电源最大可切除功率;PPV,i为光伏发电功率;PWT,i为风电输出功率;i∈Q。
可中断负荷的调节成本如下式所示:

式中:CIL,i(∙)为第i个子网采样区间内可中断负荷的调节成本;rIL,i为可中断负荷的单位调节电价;ΔPIL,i为可中断负荷的切除功率;PmaxIL,i为可中断负荷最大可切除功率;PIL,i为可中断负荷的功率;i∈Q。
可控单元的优先级原则为调节成本最小的优先级最高,调节成本最大的优先级最低。式(8)所示为第i个子网的源荷功率差ΔPMG,i分别取正、负值时,比较不同可控单元的调节成本,并依次制定各可控单元参与功率调节的优先级。

式中:Ui为第i个子网的母线电压;Ri为第i个子网与微网群连接线的直流阻抗;VES,i为第i个子网蓄电池的容量;Si为第i个子网蓄电池的SOC;ΔP为微网群的源荷功率差;i∈Q。
当ΔPMG,i=0 时,该子网内的蓄电池处于恒压控制模式,在子网功率波动时可迅速响应。当微网群功率波动时,各微网的源荷功率差、传输损耗以及蓄电池的SOC 分别作为一致性变量进行迭代。将迭代后的功率和蓄电池的SOC 代入式(10)得到蓄电池的负载率。基于离散一致性算法,各智能体一致性变量的更新方程为:
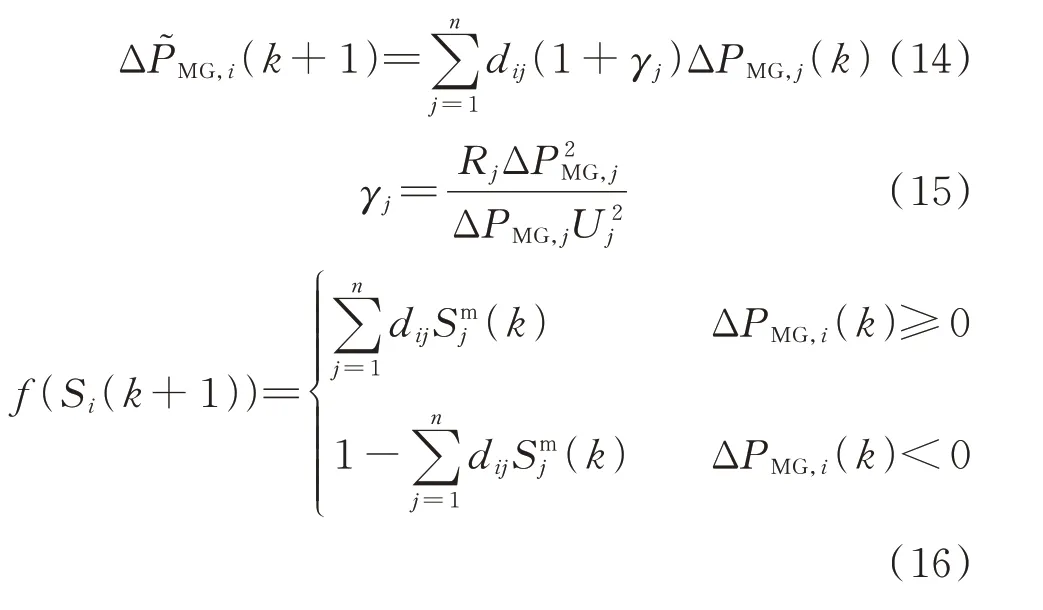

2.2 微网群的底层控制
2.2.1 可控单元功率分配
经过k͂次迭代得到蓄电池负载率λi(k͂)满足相邻2 次迭代误差小于参考值ζ,各微网根据蓄电池负载率和本地蓄电池SOC 进行功率分配如下式所示:


2.2.2 蓄电池容量选取
蓄电池主要用于补充能量短缺和吸收微网群运行过程中产生的多余能量。因此,蓄电池是一种能量型储能系统。为了确保微网群系统能够在特定条件下稳定运行特定时间,且考虑蓄电池SOC 的约束[25],微网群中蓄电池容量应该满足下式:
2.3 微网群的累积运行成本
在第2.1 节得到各可控单元的单位调节成本,第2.2 节得到各可控单元的调节功率后,即可求得由累积功率调节成本和累积传输损耗成本组成的微网群累积运行成本如下式所示。
式中:C为累计运行成本;t0为运行起始时间;te为运行结束时间。
3 仿真和实验
3.1 仿真结构及参数
本文基于MATLAB 搭建了具有4 个典型城市微网的孤岛型微网群仿真模型,其结构如附录B图B4 所示,运行数据来源于同一城市4 个不同微网。第1 个是校园微网示范工程,其负载主要是教学楼和宿舍的照明系统、路灯和浴室的锅炉;第2 个微网为公园,其负载主要是路灯、游乐场照明系统和动力设备;第3 个微网位于市图书馆,其负载主要是图书馆的室内照明和计算机中心;第4 个微网位于住宅社区,其负载主要是草坪灌溉设备、路灯和家用电器。各微网中分布式电源和负载的参数如附录B 表B1 所示。4 个微网春季典型日的运行数据如附录B 图B5(a)至图B5(d)所示。根据采集的功率和设定的电压参考值,计算出在微网与微网群间流动的电流为0~60 A。本文选用由6 根铝线和1 根钢线组成的A2/S1B 型传输导线,单根铝线和单根钢线的直径为1.98 mm,直流阻抗约为1.793 4 Ω∕km,参数如附录B 表B2 所示。底层控制采用比例-积分(proportional-integral,PI)控制器,蓄电池电流内环的PI 参数调整原理见附录C[26],电压外环与功率外环PI 控制器参数调节原理与此类似。
3.2 仿真结果
本文关于功率分配的顶层控制采样时间间隔TS=36 s;关于执行控制命令的底层控制采样时间间隔为TB=50 μs。在配置为Inter i7-11800H CPU和MATLAB 2019b 的计算机上执行控制算法,并收集在10:30—10:36 时间段执行算法10 次所用时间TE,如附录D 表D1 所示。
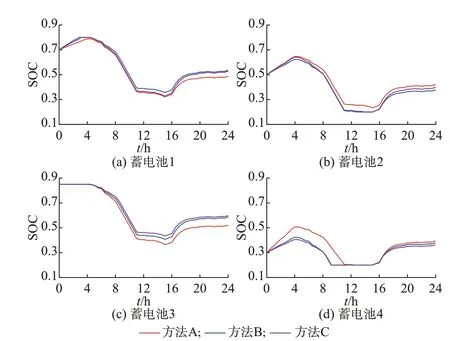
根据收集结果可知,算法执行时间TE远小于上层采样间隔时间TS;底层控制的采样时间间隔TB小于上层采样间隔时间TS,且在满足TE+TB 为了验证本文算法的实用性,对3 种功率差分配方法下蓄电池SOC 的收敛性以及微网群的运行成本的仿真结果进行了对比。 1)方法A(本文方法):以蓄电池的负载率作为状态变量。 2)方法B:以微网功率调节成本作为状态变量[21]。 3)方法C:微网群分层能量管理方法[22]。 3.2.1 蓄电池功率和SOC 收敛性对比 微网群运行期间4 个蓄电池的功率PESB和SOC在方法A、B、C 控制下的变化分别如图2 和图3 所示。在微网群运行的过程中,所有蓄电池的运行状态都是一致的,即具有同时充电或放电状态,有效避免了能量环流导致的损耗。从图2 可见,与方法B和方法C 相比,本文方法减少了由于蓄电池SOC 偏移出正常工作范围导致微网工作模式的切换次数,进而减少了其对系统稳定性冲击的次数。 图2 蓄电池功率Fig.2 Power of batteries 图3 蓄电池的SOCFig.3 SOC of batteries 在方法B 中,t=3.20 h 时,第1 个微网的蓄电池SOC 达到上限并退出运行,切除7.01 kW 分布式电源;t=9.17 h 时,第4 个 微 网 蓄 电 池SOC 达 到 下 限并退出运行,切除20 kW 负载;t=13.88 h时,第2个微网的蓄电池退出运行,切除2.79 kW 负载。在方法C 中,t=2.82 h 时,第1 个 微 网 蓄 电 池SOC 达 到 上 限并退出运行,切除7.86 kW 分布式电源;t=9.20 h时,第4 个微网蓄电池SOC 达到下限并停止运行,切 除20 kW 负 载;t=12.37 h 时,第2 个 微 网 蓄 电 池退出运行,切除1.84 kW 负载。在方法A 中,t=12.35 h 时,第4 个微网蓄电池SOC 达到下限并退出运行,切断1.44 kW 负载。 微网群中蓄电池SOC 的收敛性可由标准差表示,蓄电池SOC 的变化如图3 所示。3 种功率分配方法的蓄电池SOC 收敛性比较结果如附录D 表D2所示。与方法B 和方法C 相比,本文方法的蓄电池SOC 收敛性更好。 3.2.2 运行成本对比 图4(a)至图4(d)为各微网的实时功率调节成本,图4(e)为不考虑传输损耗的微网群实时功率调节成本,图4(f)为微网群运行24 h 的累计运行成本,图4(g)为微网群运行24 h 的累计传输损耗成本。 图4 微网群成本Fig.4 Cost of microgrid cluster 根据图4(a)至图4(e)可知,微网在2.82、3.20、9.17、9.20、12.35、12.37、13.88 h 等时间点的工作模式发生变换,微网和微网群的调节成本均增加。方法A 的调节成本比方法B 和方法C 小。 根据图4(f)和图4(g)可知,微网群的运行成本由各微网中可控单元的调节成本和微网之间能量传输损耗成本组成。基于本文提出的功率分配方法,各可控单元累计调节成本约占累计运行成本的95.18%。累计传输损耗成本约占累计运营成本的4.82%。方法A、B、C 的累计运行成本分别约为276.0、326.0、310.4 元。 3.2.3 典型日运行成本和SOC 统计数据 夏季、秋季和冬季典型日的微网群的累计运行成本分别如附录D 图D1(a)、图D1(b)和图D1(c)所示。夏季、秋季和冬季典型日的微网群中子网的SOC 变化分别如附录D 图D1(d)至图D1(g)、图D1(h)至图D1(k)以及图D1(l)至图D1(o)所示。与方法B、C 相比,本文方法的累计运行成本最小且SOC收敛速度最快。 为了进一步验证基于一致性算法得到的功率分配策略的有效性,在OPAL-RT OP5600 仿真平台上进行了硬件在环实验,数字信号处理器型号为TMS320F28335。实时仿真步长为50 μs。硬件在环实验原理如附录D 图D2 所示。 当微网群中的分布式电源功率下降或负载突然增加时,各子网电压、输出功率、蓄电池功率及其SOC 在24 s 内的变化分别如附录D 图D3(a)至图D3(d)所示。第1 个子网和第2 个子网在8 s 时切断12 kW 的分布式电源并且在12 s 时恢复。第3 个子网和第4 个子网在16 s 时增加12 kW(100%)的负载并且在20 s 时恢复。由图D3(a)可见,当切除12 kW 分布式电源时,电压下降约100 V,1.1 s 后恢复到其参考值。当分布式电源恢复时,电压上升约2.3 V,0.6 s 后恢复。当负载增加12 kW 时,电压下降约4.2 V,0.4 s 后恢复到参考值。负载恢复时,电压上升2.4 V,0.6 s 后恢复。比较图D3(c)和D3(d)可见,各蓄电池都可根据SOC 合理分配功率。为了在较短时间内观察到蓄电池SOC 的变化情况,本实验中选择了4 个0.024 kW·h 的小容量电池。硬件在环实验充分证明了本文所提控制策略的有效性。 通过对基于一致性算法的微网群功率分配方法的理论分析和仿真验证,得到以下结论: 1)蓄电池SOC 具有很好的收敛性,增强了微网群抵抗风险能力,为单个微网小功率波动的平抑提供了保障。 2)微网工作模式切换的次数减少。功率分配过程中考虑了SOC,减少了由于SOC 偏移导致的工作模式切换。当SOC 测量不准确时,基于一致性算法得到的SOC 校正策略可保证微网群正常运行。 3)当微网工作模式切换时,传输功率变化的幅值变小。当工作模式处于切换的边缘时,蓄电池的调节功率较小。当蓄电池退出运行时,相应转移到另一个单元的调节功率的幅值也较小。 4)降低了微网群的调节成本。第1 个原因是功率调节成本低的调节单元优先投入调节;第2 个原因是工作模式切换次数减少导致功率调节成本降低。 通过上述分析可知,本文所提基于一致性算法的分层协调控制方法适用于孤岛型城市微网群系统,且只需要满足微网间通信网络结构为连通图的条件,而不受微网个数的影响,具有一定的通用性。本文的关注点在于蓄电池SOC 的变化导致微网群系统工作模式的切换以及所带来的运行成本变化。如果蓄电池容量足够大,则SOC 的变化给系统带来的影响非常小,需要从其他角度对微网群的能量管理、控制策略及运行成本进行分析。值得注意的是,在通信条件较差时,微网群分布式控制可能会因为存在通信时滞和丢包而失效。在后续的研究中,将进一步探讨微网群所能容忍的时滞和丢包极限,并研究可以克服时滞和丢包的改进型一致性算法,实现对通信受限情况下微网群的有效控制。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。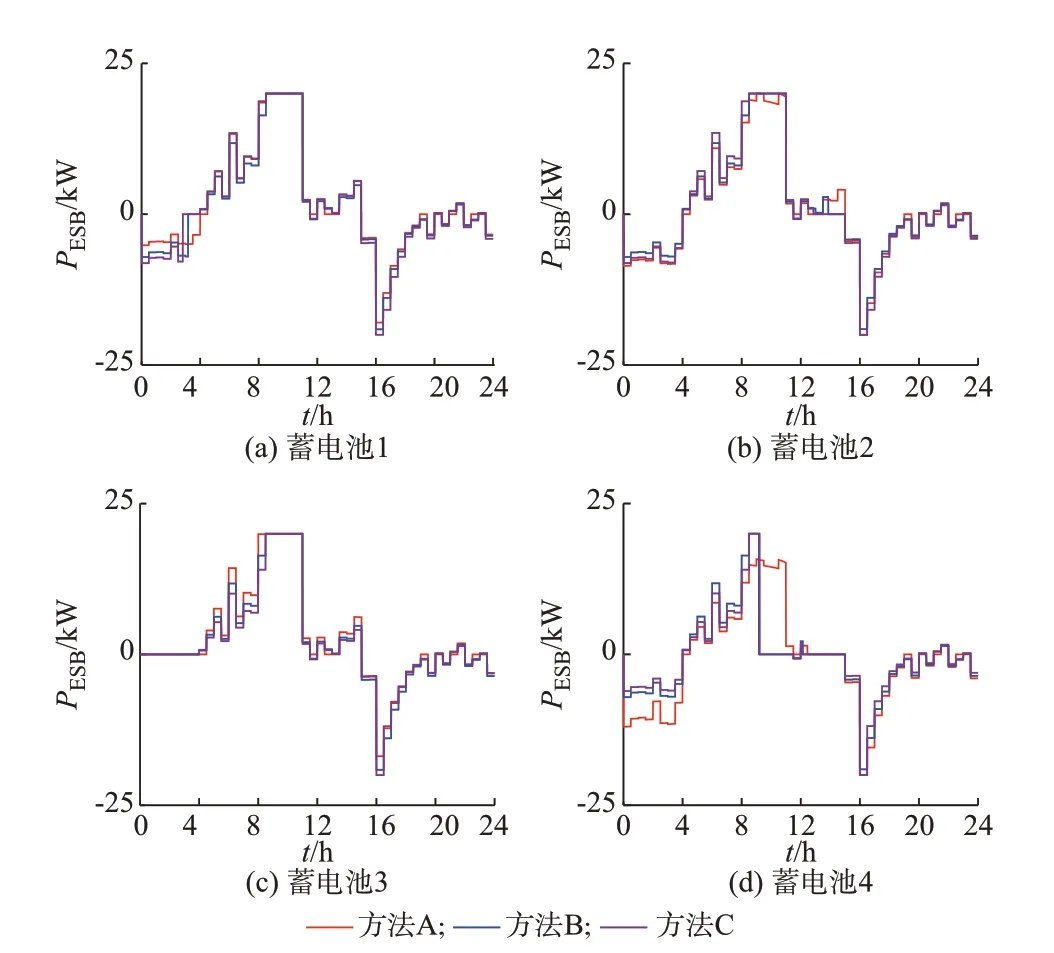

3.3 实验分析
4 结语

