特高压直流合约交易电量约束下送端电网日前调度优化

陈 浩，郝丽丽，吕肖旭，蔡霁霖，李延和，曲立楠

（1. 南京工业大学电气工程与控制科学学院,江苏省南京市 211816；2. 国网青海省电力有限公司,青海省西宁市 810008；3. 中国电力科学研究院有限公司（南京）,江苏省南京市 210003）

0 引言

“双碳”目标将推动中国新能源的高速发展,预计到2030 年,风电和太阳能发电总装机容量将达1.2 TW 以上［1］。由于新能源装机与负荷逆向分布、灵活调节电源比重低、电网互联互通水平有限等原因,局部地区新能源消纳矛盾日益突出［2］。通过特高压直流输电将富余电力跨区外送对风光发电资源的跨区消纳起到了重要作用［3］。通常根据区间长期合约交易电量为特高压直流输电制定固定阶梯的送电方式［4］,既难以充分发挥直流输电的功率调节潜力,又无法适应送端电网风电和光伏等新能源发电出力的随机性和波动性,易引起送端电网新能源的弃电,增大送端电网传统机组的调峰压力。

目前,电力系统通过直流联络线跨省跨区调度的研究多集中于省区级的安全约束经济调度优化［5-6］。文献［5］建立了考虑无功设备动作次数的交直流互联电网日前两阶段随机优化调度模型；文献［6］建立日前-日间直流功率调整约束模型,在日前优化结果的基础上对日间直流联络线功率进行调整,促进新能源跨区消纳。现有涉及直流输电计划的研究多侧重于在日前或日间对已知直流日外送电量进行优化分配。然而,对于已知年、月等较长时间尺度的直流外送合约交易电量,如何由其得到日交易电量却少有研究。此外,由于实际运行场景的动态变化,还需要根据每日实际输送的电量自适应更新后续剩余的合约电量及其分配计划。

对于电网中渗透率逐渐增大的随机性电源,近年来,国内外学者对不确定性机组组合问题进行了大量研究,相继提出了场景法［7-9］、机会约束规划［10-12］和鲁棒优化［13-15］等方法。其中,场景法与机会约束规划中随机性电源出力分布概率较难准确获取,使得优化结果存在安全风险,而鲁棒优化决策的优化结果偏保守。为解决上述矛盾,部分研究结合机会约束规划和鲁棒优化,建立了分布鲁棒优化方法［16-22］。根据引入的描述随机变量的概率分布集合（模糊集合）的不同,分布鲁棒调度有不同的决策模型及对应的处理方法。文献［20］提出了一阶、二阶矩约束下的分布鲁棒优化,其集合中分布类型不固定,矩信息也不固定,且考虑了各不确定量之间的相关性。在此基础上,文献［22］利用该分布集合,提出一种新的模型等价转化方法。该方法将原问题等价转化为二次约束二次规划（quadratically constrained quadratic programming,QCQP）问题,并使用重构线性化技术（reformulation linearization technique,RLT）松弛模型对含风电和火电机组的系统进行实时调度优化。电网经济调度研究中所涉及的常规机组多为火电机组,对水电、抽水蓄能等机组涉及较少［23］。中国西北地区有较多富余的水力和风光发电资源,大量的清洁能源发电通过省际直流输电送出,计及水力发电的季节特性和库容约束进行生产模拟尤为必要。

针对上述问题,本文建立了考虑长期合约交易电量约束的新能源高占比送端电网随机生产模拟两层框架。参照中国西北某省级送端电网的能源构成和分布建立算例,对所提框架及方法的有效性进行了仿真验证。

1 随机生产模拟框架

本文在特高压直流长期合约交易电量约束下,建立了统一多个时间尺度的新能源高占比送端电网随机生产模拟两层框架。根据系统多年历史运行数据提取不同时间尺度的负荷特性和新能源出力特性信息,迭代优化各月、各日直流外送电量分配。同时,跟踪实际执行过程更新后续生产模拟结果,根据负荷及新能源预测信息迭代优化小时尺度的直流外送功率和机组出力。框架充分兼顾不同时间尺度信息的完备性和准确性,由全面、低精度、大时间尺度的整体电量规划到局部、高精度、小时间尺度的运行方式计划,提高优化的可靠性。随机生产模拟框架如图1 所示。

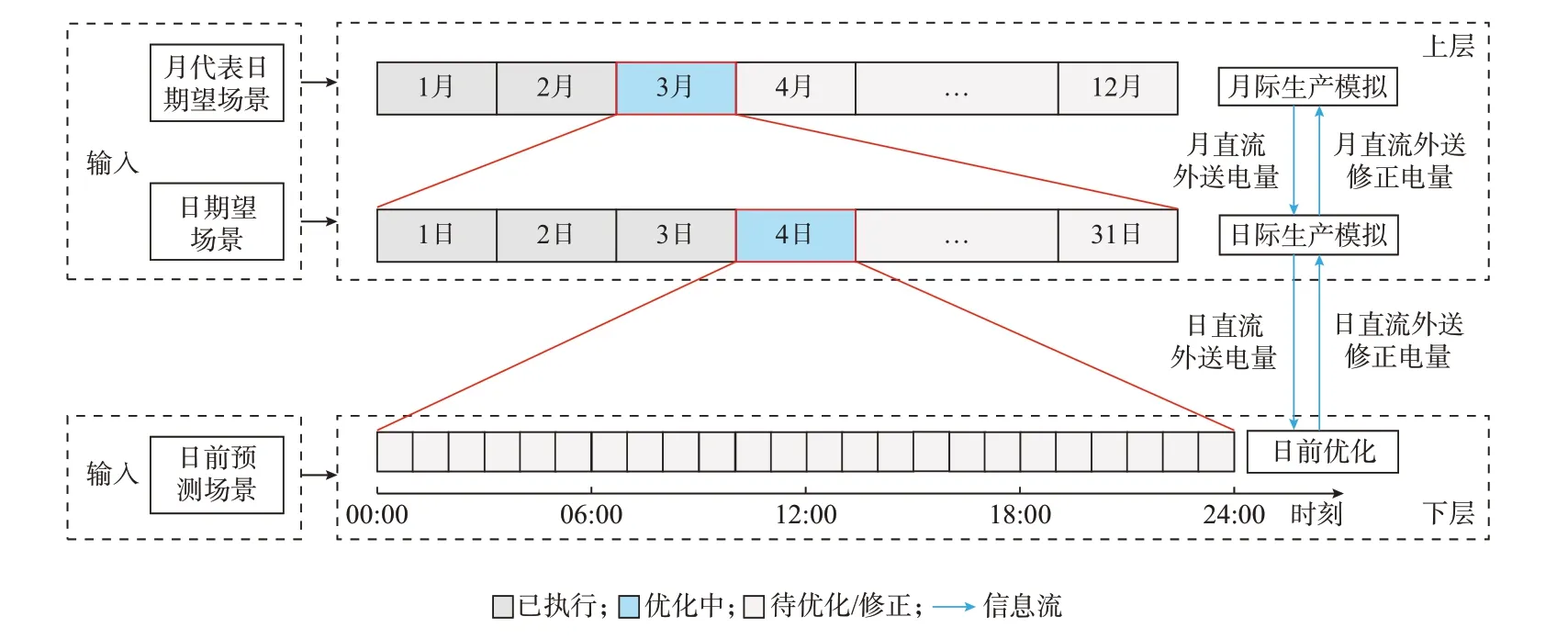
图1 随机生产模拟两层框架Fig.1 Two-layer framework for stochastic production simulation

1）框架上层

框架上层通过月际生产模拟、日际生产模拟及二者间的迭代,可以在月、日时间尺度上得到待优化目标年或月内送端电网日直流外送电量。其中,月际生产模拟所需待优化目标月的代表日及其期望场景和日际生产模拟所需待优化目标月内各日的期望场景,均根据历史数据所表征的电网负荷特征和新能源出力特征得到。

月际生产模拟根据各月代表日期望场景,在全年及各月合约外送电量的约束条件下,优化送端电网各月的直流外送电量分布。据此,日际生产模拟根据待优化目标月内各日的期望场景,对目标月直流外送电量进行逐日优化分配。当分配结果无法满足系统某月的运行约束时,将分配给该月的固定外送电量作为月外送电量约束,优化其各日的直流外送电量,并用各日直流外送电量之和作为月直流外送修正电量返送至月际生产模拟,重启月际生产模拟为未执行的各月进行电量优化,直至上层迭代结束。可在年前进行长周期生产模拟确定次年的直流外送电量分配预案,或在年内执行过程中和下层配合修正未执行各月的直流外送电量。

2）框架下层

框架下层根据日际生产模拟优化得到的日直流外送电量,结合日前预测场景,优化得到次日该系统的直流外送功率。日前优化根据更为准确的日前预测场景,并充分利用直流联络线的调整能力,对日际生产模拟下送的日直流外送电量进行有偿调整,调整量作为日直流外送修正电量返送至日际生产模拟。

3）上下层迭代优化

上层日际生产模拟优化得到的日直流外送电量送至下层日前优化,为保证日前优化的经济性,该部分的直流外送电量为有偿可调。调整后的日直流外送修正电量上送并重启日际生产模拟,对该月剩余日进行电量重新分配。当该月迭代结束后,返送月直流外送修正电量,重启月际生产模拟对剩余月进行电量优化,直到完成全年计划。

4）新能源出力不确定性的处理

考虑到中长期的负荷和新能源出力预测精度有限,在上层月际、日际生产模拟中,基于长期历史数据计算期望场景以反映系统的不确定性,以最小化期望场景下的运行成本为目标,在确定的约束条件下进行长周期随机生产模拟。

日前预测场景准确性较好,但实际运行中仍存在预测误差,给系统安全运行带来隐患。故下层选用了不确定分布集合［20］来描述新能源机组出力预测误差。基于此,以最小化预测场景下的运行成本为目标,在含有随机变量的约束下进行短周期分布鲁棒优化。

2 月际-日际生产模拟

2.1 月际-日际生产模拟目标函数

长周期随机生产模拟的目标为最小化期望场景下的总运行成本:

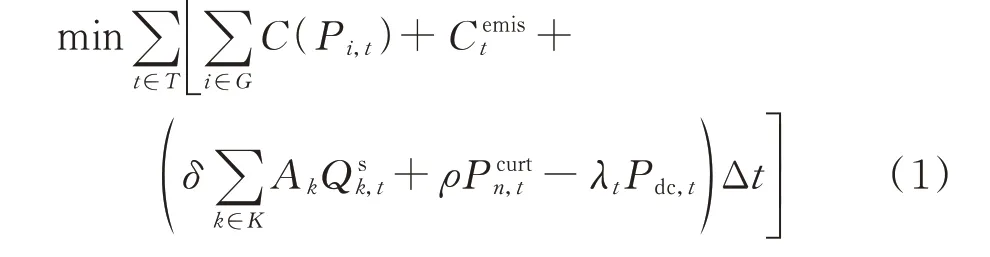
式中:T为计算周期内时段集合；Δt为各时段时长；G为火电机组集合；Pi,t为火电机组i在t时段的有功出力；C(∙)为发电成本函数；Cemist为系统在t时段的排放成本；δ为水电上网电价；K为水电站集合；Ak为水电站k的发电出力系数；Qsk,t为水电站k在t时段的弃水流量,该水量无法进入水电机组发电,因此会产生一定损失；ρ为新能源弃电罚因子；Pcurtn,t为新能源机组n在t时段的弃电功率；λt为t时段直流外送电价；Pdc,t为t时段的直流外送功率。

火电机组i在t时段的发电成本为:

框架上层的月际-日际生产模拟具体流程见附录A 图A1。

2.2 月际-日际生产模拟约束条件

2.2.1 系统运行约束

1）功率平衡约束

2）支路潮流约束

当节点负荷需求在静态安全域内变化时,要保证支路传输功率不超过允许的安全范围,应采用基于直流潮流的转移分布因子来描述这一约束［24］:

2.2.2 火电机组约束

火电机组约束包含出力约束和爬坡约束,具体可见附录A 式（A1）和式（A2）。

2.2.3 水电机组约束

水电机组约束包含出力约束、水库库容约束、发电流量约束、弃水流量约束、水量平衡方程约束以及水电机组出力表达式,具体可见附录A 式（A3）至式（A8）［25］。

2.2.4 新能源机组约束

1）出力约束

3 日前分布鲁棒优化

3.1 日前分布鲁棒优化目标函数

日前优化目标为最小化预测场景下的运行成本:

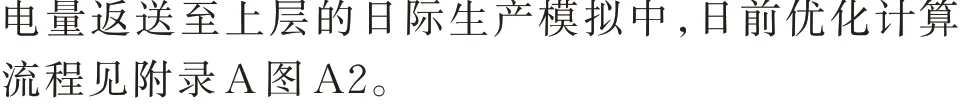
3.2 约束条件和分布集合的构建

3.2.1 约束条件

式中:Pb,t为支路b在t时段的传输功率；KGb、KJb、KNb分别为火电机组节点、水电机组节点、新能源机组节点对支路b的注入转移分布因子向量；PG,t为t时段所有火电机组出力向量；PJ,t为t时段所有水电机组出力向量；PN,t为t时段所有新能源机组出力向量。

6）其余约束

其余约束同附录A 式（A2）、式（A4）至式（A8）及式（8）至式（10）。

3.2.2 分布集合的构建

本文选用文献［20］所提出的不确定集合来描述Ωt的不确定性,表达式为:

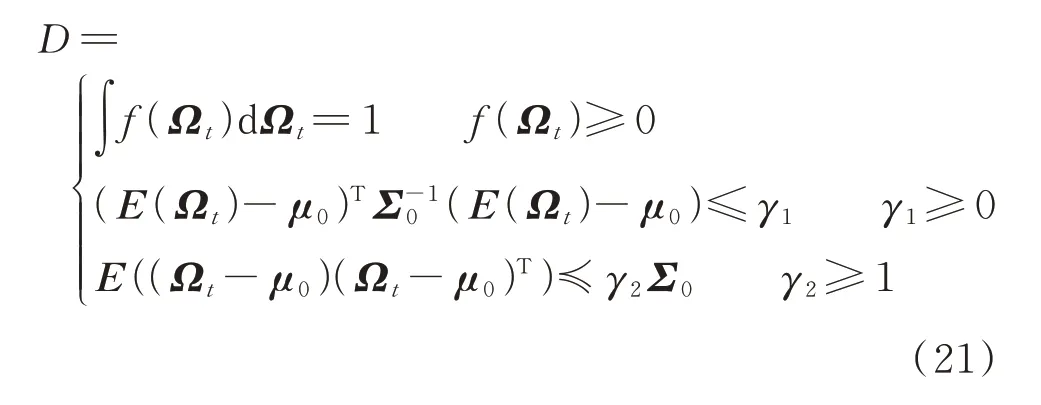
式中:f(Ωt)为Ωt的联合概率密度函数；μ0和Σ0分别为Ωt的一阶矩与二阶矩的统计值向量；γ1为期望的椭球不确定集半径的限定参数；γ2协方差矩阵的半定锥不确定集范围的限定参数；E(∙)为期望运算函数；≼为半负定符号。

综上,式（13）至式（21）构成了短周期分布鲁棒优化模型。但由于鲁棒机会约束直接求解具有一定的困难,下文将介绍如何将其等价转换为易于求解的模型。

3.3 模型的转换与求解

上述短周期分布鲁棒优化模型求解的关键在于对式（18）至式（20）的等价转换。文献［21］给出一种等价转换方式并进行了证明,本文参考该方法将式（18）至式（20）等价转换为式（22）至式（25）,从而形成确定性的QCQP 优化问题。具体转换过程详见附录B［26］。

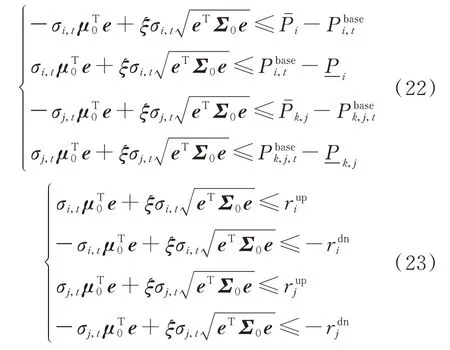
4 算例分析

参照中国西北以清洁能源为主的某省级送端电网的能源构成及其时空分布,并结合其受端电网条件,本文对IEEE 10 机39 节点系统进行改进,构建送、受端直流互联算例系统,如图2 所示。送端电网按其电源特性分为A、B、C、D、E 这5 个区域。送端电网的新能源机组集中分布于A、D 区域,其中,风电场G6、G7分别接于母线30 和31,光 伏电站G8、G9分别接于母线32 和37。C 区域包含了大部分的水电站和火电厂,其中,G3设置为调频电厂。另有一部分水电站位于B 区域,即水电站G5。火电机组的相关参数见附录C 表C1。设置丰水期为5 至10 月,其余月份为枯水期,丰、枯水期水电站的出力、排水量和库容约束等设置参见表C2 和表C3。E 区域无电源无负荷,仅作为功率交换区域。受端电网用火电厂G10和负荷进行等值。部分参数的设置详见附录A。本文基于MATLAB 平台,利用Yalmip 工具包并调用CPLEX 求解器进行求解。

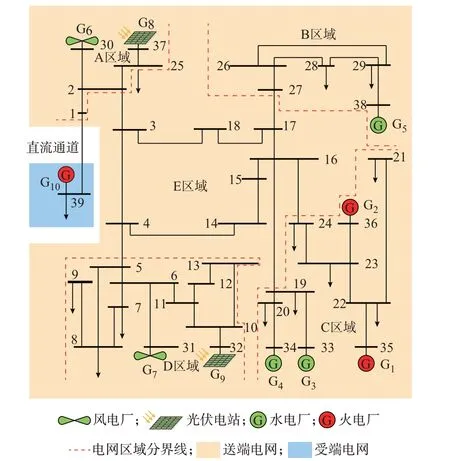
图2 改进的IEEE 10 机39 节点系统Fig.2 Improved IEEE 10-generator 39-bus system

4.1 月际-日际生产模拟算例

采用本文所提框架上层为送端电网待优化年进行月际-日际生产模拟,在2 月的日际优化阶段产生了月直流修正电量,重启月际生产模拟。在后续的迭代过程中,8、11 月也分别产生了月直流修正电量,按相同的策略处理,最终得到优化年各月、日的直流外送电量。其中,月直流外送电量的上层优化结果见图3（a）；以枯水期中的1 月、丰水期中的7 月为例,其日直流外送电量的上层优化结果分别见图3（b）和（c）。

由图3（a）可知,5 至10 月各月直流外送电量整体较高,其中,5 月外送电量为全年最高。1 至4 月和11 至12 月的月直流外送电量较小,11 月外送电量为全年最低。由图3（b）和（c）可知,7 月各日直流外送电量差别较小,且大多明显高于1 月各日直流外送电量,而1 月各日直流外送电量差别较大。主要原因为送端电网的常规机组大多为水电机组,5 至10 月处于丰水期,为了减少弃水,限制了各水电站的出力下限。因此,丰水期和枯水期的直流外送电量存在差异。

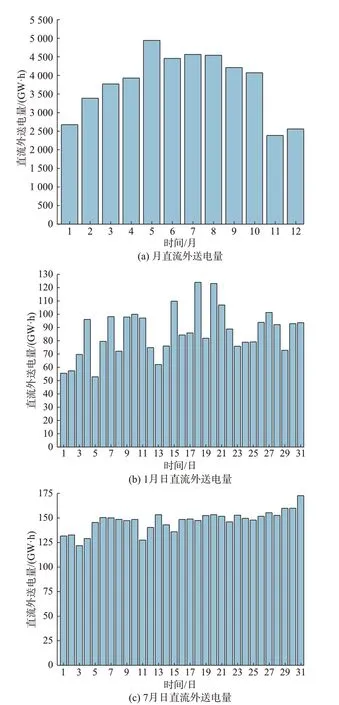
图3 直流外送电量Fig.3 Electricity quantity of DC transmission

4.2 日前分布鲁棒优化算例

执行至1 月21 日时,对1 月22 日进行日前调度优化,得到优化结果如图4（a）和附录C 图C1、图C2所示。与1 月22 日的日期望场景及日际直流送电计划相比可知:9～12 h 时,送端电网新能源出力大发,使得上层日际直流送电优化过程中已按单次最大直流调整幅度上调外送功率,日前优化时不再具有上调空间。因此,日前直流外送结果仍与日际优化结果接近；13～24 h 时,日前预测场景的新能源出力大于日期望场景,且直流外送上调空间充足,因此,日前优化进一步提高了新能源的消纳。

执行至6 月30 日时,对7 月1 日进行日前调度优化,结 果 如 图4（b）和 附 录C 图C3、图C4 所 示。与7 月1 日的日期望场景及日际直流送电计划相比可知:1）因当天预测的次日新能源出力总体减少,故日前调度优化得到的日直流送电量大多较日际优化结果有所降低；2）在日前预测新能源出力减少的情况下,7～12 h 时直流联络线的日前优化外送功率反而较日际外送功率增加,因为7 h 时G2至G5均处于满发状态,为确保机组调整因数约束式（17）和鲁棒机会约束式（22）成立,即机组调整因数不允许同时为0,需要增大G1出力以预留足够的下调峰能力。因此,7 h 时的直流外送功率增加,且直流调整结束后还需在一段时间内保持外送功率恒定,导致7～9 h时外送功率整体上升。

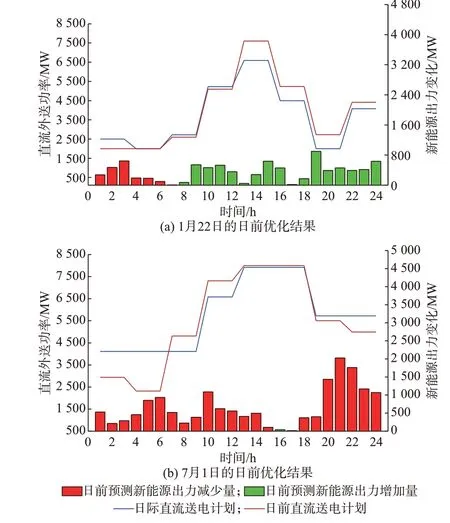
图4 日前优化结果Fig.4 Results of day-ahead optimization

日前优化中产生并返送给日际生产模拟的日直流外送修正电量分别如附录C 图C5 和图C6 所示。全年优化结束后,各月的月修正电量如图C7 所示。观察月修正电量可以发现,1 至4 月和11 至12 月的各月修正电量均为正,5 至10 月的各月修正电量均为负,呈明显的丰、枯水季节特性,且枯水期修正电量的绝对值明显大于丰水期,说明枯水期各日日前优化的日修正电量较大,而丰水期则偏小,与图C5和图C6 的结果一致。由此可以看出,对于有较多水电接入的电网,其丰、枯水季节特性对新能源消纳和电能调度有较大影响。

4.3 调度方法对比分析

为验证本文所提方法的有效性,设置其他2 种调度优化方法进行对比分析。

方法1:结合系统的待优化运行方式,采用文献［7］的方法模拟新能源的随机出力场景并进行场景筛选,随后启动日前调度优化,其中直流联络线功率控制方式与本文所提方法一致。

方法2:在本文方法基础上,仅将直流联络线交换功率的调整方式根据送端电网负荷的峰谷时段设置为传统的两段式［6］,峰时段为9～21 h,其余为谷时段。

方法3:本文所提调度优化方法。

方法1 至3 计算得到的直流送电计划如图5 所示。方法2、3 均采用本文所提方法来反映新能源出力的不确定性,仅直流送电调整能力不同,其中方法2 因日直流外送调整能力仅根据送端负荷的峰谷时段进行调节,故外送水平明显较低,主要体现为直流外送曲线无法根据新能源出力进行灵活调整。方法1、3 的直流外送调整能力均灵活设置,且约束相同,仅在新能源出力随机性的处理上不同,所以2 种方法得到的直流外送功率均能灵活跟踪送端新能源出力的时序分布,促进风光资源跨区消纳。方法1 通过场景筛选扣除了高风险场景的影响,因此,其直流外送整体水平较高,但具有一定运行风险。设算例系统中各新能源电站的输出功率服从高斯分布,通过随机抽样得到各电站的日出力曲线作为实际运行场景,用上述3 种方法得到的出力计划来模拟运行,判断是否满足机组出力约束、系统备用约束及支路潮流约束。通过对实际运行场景进行多次模拟（本文设为1 000 次）,统计不满足约束的次数占模拟总数的比值,作为越界概率以衡量运行风险,结果如表1 所示。

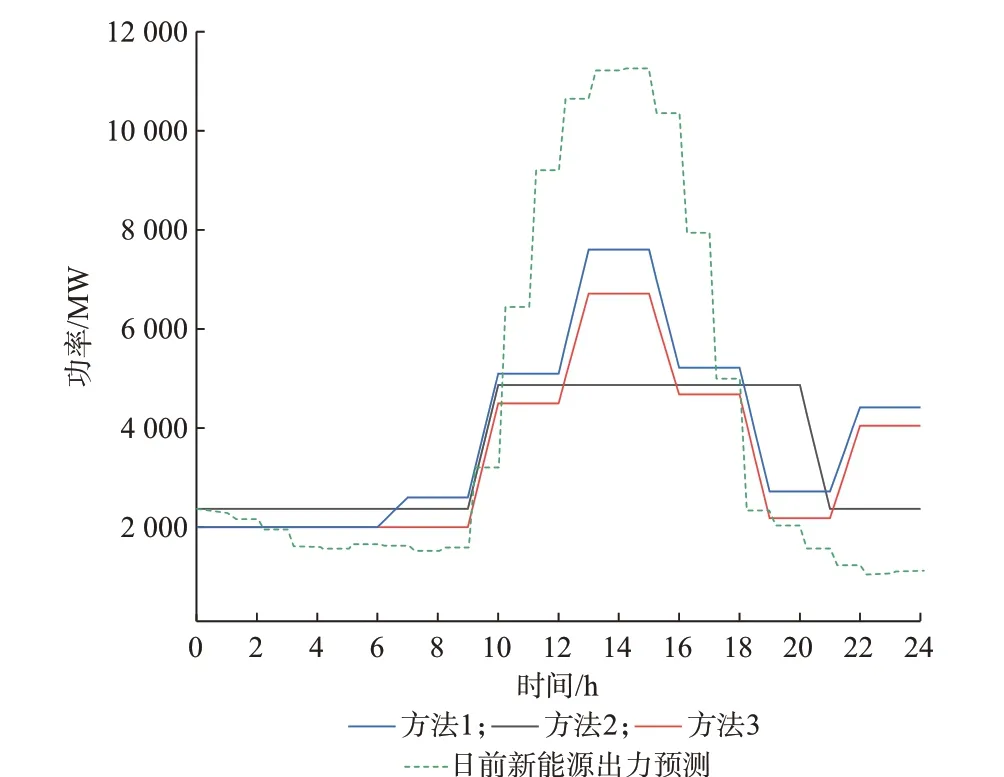
图5 不同方法下直流外送计划对比Fig.5 Comparison of DC transmission plans with different methods

由表1 可知:1）从日（年）收益和弃电率的角度,方法1 和3 明显优于方法2,说明灵活的直流外送调整能力可以大幅度改善系统对新能源的消纳水平,并提高系统运行经济性,其中,方法1 对于新能源消纳和收益的提高效果较方法3 更为明显；2）从系统安全性的角度,方法1 的越界概率远远超过了本文设定的风险系数ε=0.2。这意味着如果不充分计及新能源的不确定性,而是冒进地安排运行方式,会使系统面临较大的安全风险。方法3（本文方法）对应的越界概率仅为0.08,远小于本文设定的风险系数。这也充分说明本文所采用的鲁棒机会约束方法可以有效保证高占比新能源送端电网的安全运行,同时兼顾其经济性和新能源的消纳水平。

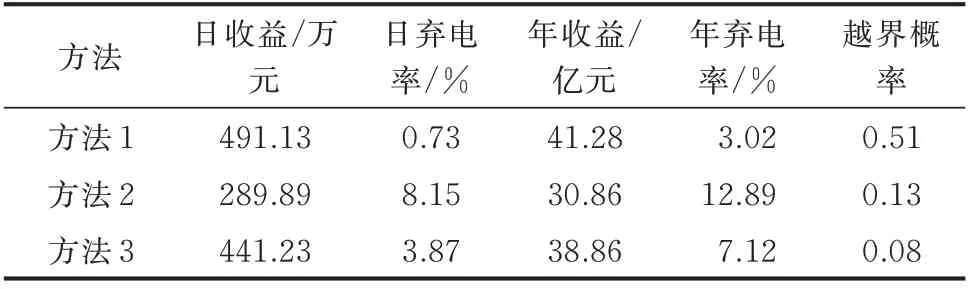
表1 不同方法的优化结果对比Table 1 Comparison of optimization results with different methods

5 结语

本文面向清洁能源高占比送端电网,建立了考虑长期合约交易电量约束的随机生产模拟两层框架。通过理论研究和仿真验证得到结论如下:

1）将直流联络线日外送电量由固定值变为由长、短周期的上下层协调优化得到,以适应新能源出力、负荷或系统运行条件等的不确定；

2）将直流联络线的调整方式由传统的两段式调整为多段阶梯式,可以充分利用其调整能力,促进送端电网的新能源消纳；

3）在下层采用分布鲁棒优化方法处理新能源出力的随机性,兼顾系统运行的安全性和经济性；

4）对于水电资源富集的电网,充分计及水力发电的丰、枯水季节特性和库容约束,可以有效调度水电机组的调峰能力。

本文在省间电力交易环节的设置较为简单,后续拟进一步细化相关研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。