微型空气压缩机组合式曲轴的扭振分析

李程翊，吴伟烽，李晓然，张 寅

(1.西安交通大学能源与动力工程学院，710049 陕西 西安；2.浙江科力车辆控制系统有限公司，324123 浙江 衢州)

1 引言

曲轴是往复压缩机中的核心的部件之一，其主要的作用是将曲轴的旋转运动转化为活塞的往复运动。在压缩机的工作过程中，曲轴承载着弯曲、轴向和扭转3个方向的交变载荷，这些交变载荷的作用会造成曲轴在这3个方向的振动，使曲轴表现出弯曲、扭转及弯扭耦合等复杂运动形态[1-3]。其中，当曲轴发生扭转共振时，会通过曲柄销对连杆及其往复质量造成冲击，这种冲击轻则使得曲柄销轴承的油膜破裂，轴瓦擦伤，重则导致曲轴发生疲劳破坏乃至断裂[4-7]。此外，曲轴的扭转振动会通过主轴承传递至机体，进而使机体辐射噪声[8-10]。因此，曲轴扭转振动直接威胁着往复压缩机的正常运行，是压缩机制造商、使用者、国内外学者所高度关注的重要内容[11]。

目前，对曲轴扭振的研究多集中在石油化工行业的大型往复压缩机中，其原因在于该类压缩机曲轴较长、往复质量及其转动惯量较大、扭转刚度较小，使得曲轴在工作转速范围内容易发生扭转共振。对于微型压缩机的轴系扭转振动特性的研究则相对较少。

本研究所使用的某微型空压机，其噪声明显超标。通过近场法对机体噪声进行1/3倍频程测试后发现，声压级峰值出现在1250 Hz左右，且曲轴箱是整机噪声较高的部分。而轴系振动是曲轴箱主要的振动来源，因此有必要对空压机轴系的振动进行进一步的分析。首先采用常惯性质量模型[12，13]分析了曲轴的模态，得到了曲轴的各阶固有频率和模态振型；并进一步对引起曲轴发生扭转变形的切向力进行了谐波分析，结合模态分析的结果阐明了轴系不会发生扭转共振。

2 模态分析的基本原理

动力学通用方程为

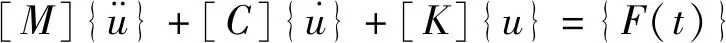
(1)

式中 [M]——整体质量矩阵

[C]——阻尼矩阵

[K]——整体刚度矩阵

F(t)——外部动力载荷

u——位移

模态分析的基本方程为

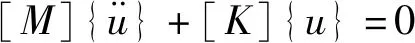
(2)

令u=Usin(ωt) ，方程变化为

(3)

求解上式即可得到结构的固有圆频率ωi和振型φi。本文通过ANSYS有限元软件提取轴系的模态参数。

本研究所用轴系是结构复杂的装配体，有三大特点：(1)曲柄滑块机构为变转动惯量系统，通常的处理方法是转化为常惯量，即将往复质量的影响视为其一半集中在曲柄销处随后者一起回转；(2)曲轴各部件之间通过螺栓紧固，始终保持紧密接触，且模态计算为线性分析，故将接触类型处理为绑定；(3)轴系与曲轴箱之间通过轴承约束，且工作时的额定转速为1500 r/min，计算时应予以考虑。

3 轴系模型的建立

研究所用的微型往复空压机轴系由曲轴、平衡重、电机主轴及转子、往复质量等四部分构成，其各段材料及关键参数汇总如表1所示。

表1 轴系各段材料及属性

3.1 结构简化及网格划分

根据曲轴的结构形状特点，以有限元计算的数据准备工作量、求解时间及精度等为基本尺度，在不影响轴系动力学特性的前提下，需要对曲轴建模结构进行简化[14]。

曲轴结构中存在圆角、倒角、螺纹孔、螺栓、间隙等结构，参考其他学者的研究，忽略这些细小结构并重新修正几何模型[15，16]。修正后的模型如图1所示。

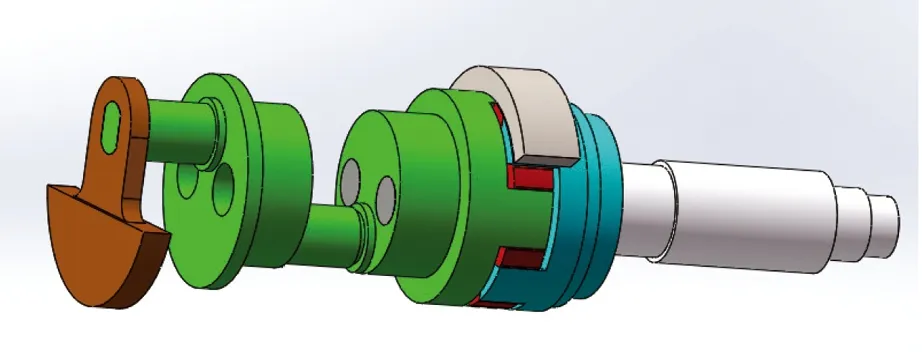
图1 曲轴几何模型

ANSYS中提供了多种网格类型，对于规则的几何结构，如平衡重、曲柄销、轴盘堵头、联轴器弹性体等部件，采用六面体网格；而对于不规则几何结构，如轴盘、电机主轴及转子等部件，采用四面体网格。通过网格无关性的验证[17，18]，最终确定网格数369568，网格节点数590558，模型网格划分如图2所示。

图2 曲轴网格划分

3.2 材料参数调整及边界条件设置

如前所述，在考虑了一半的往复质量和各连接螺栓的质量后，对各轴段的材料参数做修正，结果如表2所示。

表2 曲轴材料参数调整

空压机的额定转速为1500 r/min。曲轴在实际运行中，受到轴承的约束，仅沿着周向是自由运动的。首先对曲轴施加旋转速度进行静力计算，然后以此为边界条件，进行模态计算。曲轴的静力计算结果如图3所示。可见在额定转速下，曲轴变形量最大发生在平衡重处，最大值为0.005 mm，这是因为平衡重具有一定的重量，旋转惯性力较大；而在曲轴其他结构部分变形量均较小，几乎为0。

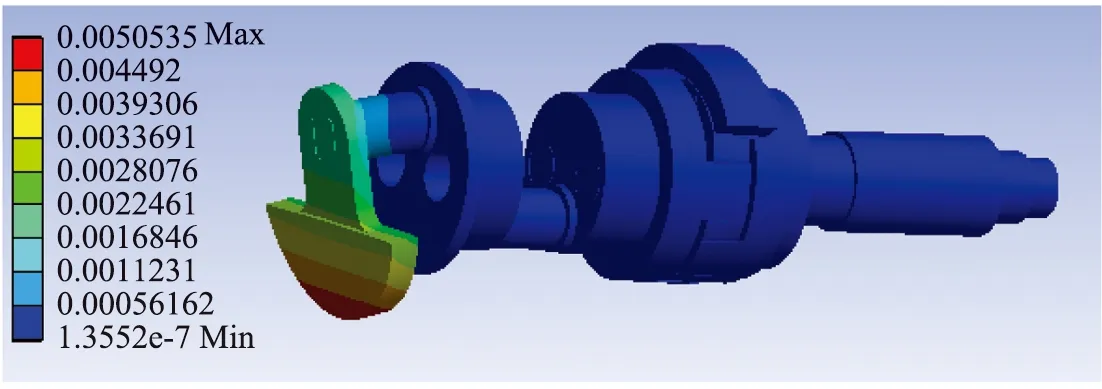
图3 曲轴总变形(单位：mm)

4 轴系的模态分析

4.1 模态参数提取结果

采用Block Lanczos法进行模态参数的提取。该法适用于大型对称特征值问题的求解，且具有较快的收敛速度[14]。提取了轴系前5阶固有频率和模态振型，结果如表3和图4所示。

图4 轴系模态振型

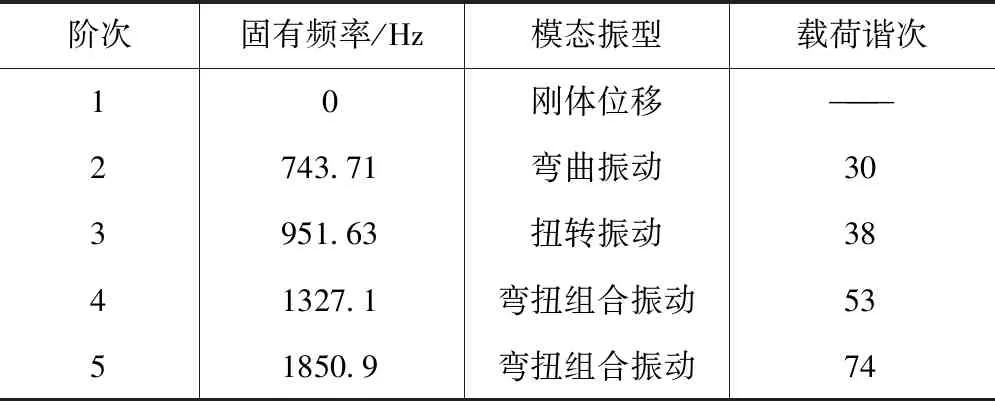
表3 轴系各段材料及属性

4.2 模态计算结果分析

从模态计算结果可见，第一阶固有频率为0，即所谓的刚体模态，这是因为曲轴的周向没有约束而解得的零特征值[19]。2～5阶为非刚体模态。第2阶固有频率为743.7 Hz，振动形式为弯曲振动；第3阶固有频率为951.6 Hz，振动形式为扭转振动；第4阶固有频率为1327.1 Hz，振动形式为弯曲和扭转振动的组合；第5阶固有频率为1850.9 Hz，振动形式为弯曲和扭转振动的组合。以上各阶模态振型的最大振幅均位于自由端平衡重边缘处。进一步分析发现，弯曲振动易发生在自由端平衡重与轴盘相连的轴段上，且自由端平衡重易发生扭转、弯曲或两者组合的振动，这是因为平衡重由于高速旋转而产生了较大的离心力。

根据美国石油协会在API618标准[20]中规定了往复压缩机的临界转速，本微型空压机的基频为25 Hz，轴系固有频率满足以上标准的要求。但轴系的各阶固有频率与载荷谐次均较为接近，故仅从模态分析还无法判定轴系是否会发生共振。本样机噪声信号的1/3倍频程分析中，中心频率位于1250Hz的频带范围为[1120 Hz，1410 Hz]，包含了轴系第4阶固有频率(1327.1 Hz)。因此有必要做进一步分析，判断轴系是否发生了共振。

5 切向力谐波分析

为了进一步确定轴系是否发生扭转共振，需要对引起轴系产生扭转共振的激振力——切向力进行谐波分析。图5～7表示了分别额定工况下4500 Hz内的一、二级切向力及总切向力的谐波分析结果，即切向力的幅频特性。

由图5、图6和图7可知，第一列切向力的主要幅值有4个，从高到低依次为616.0 N、304.0 N、231.7 N和86.9 N，分别对应基频和第2、3、4倍谐频；第二列切向力的主要幅值有4个，从高到低依次为 1166.6 N、376.5 N、234.6 N和89.1 N，分别对应基频和第2、3、4倍谐频；总切向力的主要幅值有4个，其中2倍谐频对应峰值674.4 N，基频对应次峰573.2 N，4倍谐频和6倍谐频分别对应第三峰值176.0 N和第四峰值87.7 N。但在可能引起轴系共振的各阶谐频(750 Hz、950 Hz、1325 Hz、1850 Hz、2125 Hz、3550 Hz、3800 Hz、4250 Hz)处，一级切向力幅值均小于3N，二级切向力幅值均小于3.5 N，总切向力幅值均小于5 N。这说明额定工况下轴系所受切向力在各固有频率附近的谐频处的能量微乎其微，压缩机轴系不足以发生扭转共振。

图5 一级切向力谐波分析

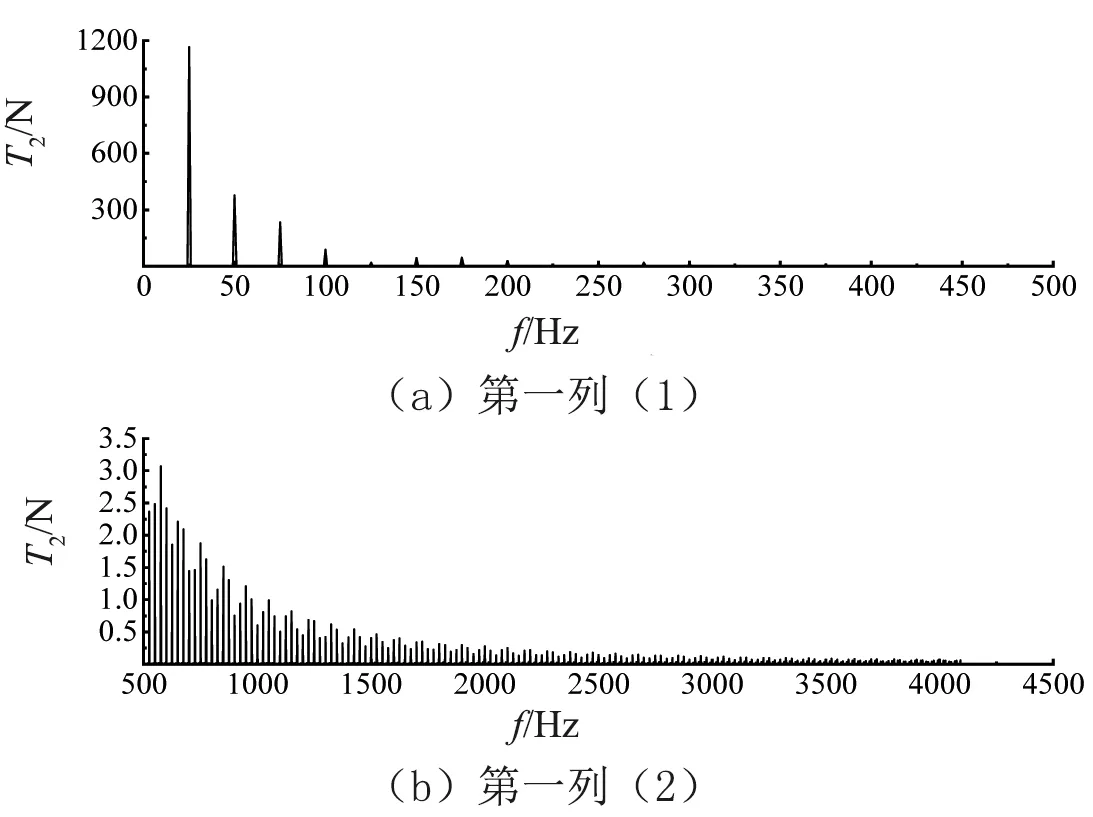
图6 二级切向力谐波分析

图7 总切向力谐波分析

6 结论

本文对微型空气压缩机轴系的扭振特性进行了研究。

首先结合本样机轴系的装配体特性，对模型进行了适当处理；采用常转动惯量模型处理往复质量的影响，并在考虑了实际工程约束和转速的基础上，采用有限元技术对轴系进行了静力计算。接着以静力计算的结果为边界条件，提取了轴系前5阶的固有频率和模态振型，分析发现其30倍频、38倍频、53倍频和74倍频分别落在轴系二阶、三阶、四阶和五阶固有频率的共振区间内，因此仅凭模态分析不足以判定压缩机的轴系是否发生了共振。

对使轴系产生扭转振动的切向力进行了谐波分析，发现这种组合式曲轴的两列曲柄销处所受切向力仅在基频和2、3、4倍谐频处存在较大幅值，总切向力仅在基频和2、4、6倍谐频处存在较大幅值，而在轴系各阶固有频率附近的谐频处切向力的幅值均很小。

本文从原理上阐明了微型两列立式往复式空压机的组合式轴系振动并不受高阶谐频载荷的影响，判断轴系在工况范围内并不会发生扭转共振。