基于平均群改进鲸鱼优化算法的最优潮流计算

陈将宏, 张晨昊, 胡炀

(三峡大学 电气与新能源学院, 湖北 宜昌 443002)

0 引言

20世纪60年代初,Carpentier[1]、Dommel等[2]提出最优潮流(optimal power flow)的概念,由于同时考虑了电力系统运行的安全性和经济性,因此最优潮流问题一直受到人们的广泛关注。初期求解电力系统最优潮流一般使用传统的数学规划类方法,如牛顿法[3]、二次规划法[4]、线性规划法[5]和内点法[6]等。最优潮流的约束条件复杂，极值多,是一个非线性非凸优化问题[7],在使用传统的数学规划类方法时,一般需要计算目标函数对控制变量的一阶或二阶梯度,并且当初值落入局部最优点的收敛域内时,整个搜索过程易陷入局部最优,导致其在大规模非线性优化问题中的使用受限。相比之下，智能优化算法的结构简单,内在并行性较强,对目标函数和约束条件没有任何限制,当遇到非连续、非光滑和高度非线性解空间的复杂问题时,能够通过迭代更新随机解集,十分灵活的寻找最优解,解决了传统数学方法求解电力系统最优潮流问题的缺陷。随着研究不断深入,求解最优潮流问题的智能算法主要分为两大类：一类是进化算法,例如遗传算法(genetic algorithm,GA)[8]、差分进化算法(differential evolution algorithm,DE)[9]等；另一类则是群智能算法,例如粒子群算法(particle swarm optimization,PSO)[10]、飞蛾扑火算法(moth-flame optimization,MFO)[11]、人工蜂群算法(artificial bee colony,ABC)[12]、樽海鞘群算法(slap swarm algorithm,SSA)[13]和灰狼优化算法(grey wolf optimizer,GWO)[14]等。文献[8]和文献[9]采用GA和DE算法求解最优潮流问题,具有编程简单且寻优速度较快等优势。文献[11]和文献[12]提出的MFO和ABC算法,虽然初始值较大,但是在迭代初期的下降性能好,有效提升了最优潮流的寻优精度。近年来,应用于求解最优潮流问题的智能算法越来越多,无论是进化算法还是群智能算法,想要得到理想的优化结果都要依靠算法本身的全局搜索和局部开发能力,因此如何在算法设计中寻求平衡成为了现阶段研究的重点。文献[13]针对SSA算法全局搜索能力差、易陷入局部最优的缺点,通过在位置更新公式中加入随机突变因子并结合自适应权重来提高算法的收敛性能和搜索效率。文献[14]提出的CS-GWO算法,在原有灰狼算法独特的双搜索寻优方式中加入交叉搜索机制,强化了算法跳出局部最优的能力。文献[15]提出一种聚类的差分进化算法,将优化过程分为2个阶段,在第一个阶段中将DE算法和聚类相结合快速确定局部最优解区域,在第二个阶段中采用局部优化方法高速收敛得到最优解。

鲸鱼优化算法(whale optimization algorithm,WOA)由澳大利亚学者Seyedali Mirjalili于2016年提出,该算法模拟了座头鲸特有的泡泡网觅食行为,通过包围猎物、搜索猎物、螺旋更新3个阶段,不断接近最优解[16]。文献[16]中,利用23种基准测试函数对WOA算法进行检验,结果显示WOA算法具有良好的全局寻优性能和搜索精度,收敛速度也明显优于大多数经典智能算法的。并且当把WOA算法运用在张力、压缩弹簧和焊接梁等机械设计中,该算法在处理这类多随机变量的问题时具有较为明显的优势。文献[17]和文献[18]提出,将WOA算法运用在机械臂轨迹规划和锂电池充电方法中,能够有效提升其工作效率。

针对WOA算法本身仍然存在求解精度较低、收敛速度较慢和易陷入局部最优等缺点[19],提出一种平均群改进鲸鱼优化算法(average swarm improved whale optimization algorithm,AWOA)求解电力系统最优潮流问题。

1 最优潮流的数学模型

最优潮流问题的主要目的是通过调整电力系统中的控制变量如发电机输出功率、可调变压器抽头等来寻找能满足所有运行约束条件的,使系统的某些性能指标(如发电成本或网络损耗)达到最优值时的潮流分布[1]。数学上可表示为

minF(x,u),

(1)

(2)

式中：F代表待优化的目标函数；x、u分别为状态变量、控制变量；g(x,u)、h(x,u)分别代表等式约束、不等式约束。

1.1 状态变量和控制变量

状态变量x可表示为

x=[PG1,V1，V2，…，VNb,QG1，QG2，…，QGNg,SL1，SL2，…，SLNl],

(3)

式中：PG1为平衡节点的有功出力；V1,V2，…,VNb为负荷节点的电压幅值；QG1，QG2，…，QGNg为发电机的无功出力；SL1，SL2，…，SLNl为支路容量约束,其中Nb、Ng、Nl分别为系统负荷节点、发电机、支路的总个数。

控制变量u可表示为

u=[PG2，PG3，…，PGNg,VG1，VG2，…，VGNg,T1，T2，…，TNt,QC1，QC2，…，QCNc],

(4)

式中：PG2，PG3，…，PGNg为除了平衡节点外,其他发电机的有功出力(通常将第一台发电机设为平衡节点)；VG1，VG2，…，VGNg为发电机节点的机端电压；T1，T2，…，TNt为可调变压器变比；QC1，QC2，…，QCNc为无功补偿装置输入的无功功率,其中,Ng、Nt、Nc分别为系统中发电机、变压器和无功补偿装置的总个数。

1.2 等式约束

最优潮流的本质是潮流计算,需满足系统中各节点的功率平衡约束。

(5)

(6)

式中：PGi、QGi分别为发电机i的有功、无功出力；PDi、QDi分别为节点i的有功、无功功率；Gij、Bij、δij分别为节点i、j之间所连支路的电导、电纳、两节点之间的相位差；Vi、Vj分别为节点i、j的电压;N为系统总节点数。

1.3 不等式约束

式(3)中状态变量的不等式约束包括平衡节点有功出力、节点电压幅值、发电机无功出力约束和支路容量约束。

(7)

(8)

(9)

(10)

式(4)中控制变量的不等式约束包括发电机有功出力、电压约束；变压器变比约束和无功补偿上下限约束。

(11)

(12)

(13)

(14)

1.4 目标函数

选取发电成本、网络损耗、发电成本与网络损耗加权和、发电成本与电压偏移加权和为目标函数。

① 发电成本。

(15)

式中ai、bi、ci分别为发电机i的成本系数。

② 网络损耗。

(16)

式中PDi为节点i的负荷功率。

③ 发电成本与网络损耗加权和。

(17)

式中:Ploss为系统的网络损耗；wloss为网络损耗的权值系数,文中取1 950[11]。最优潮流问题往往不能单纯的考虑发电成本或者网络损耗,有时需要将两者结合起来,在降低网络损耗的前提下尽可能提高系统运行的经济性。

④ 发电成本与电压偏移加权和。

(18)

式中:wv为电压偏移的权值因子,文中取100[20]。负荷节点电压是电力系统的安全指标和服务质量指标,过度追求降低发电成本可能会导致电压质量无法达到规定要求,因此要同时考虑发电成本和节点电压偏移。

为了解决不等式约束在求解过程中的越限问题,可以利用惩罚函数予以纠正。在目标函数后加上状态变量的约束限制,得到完整的目标函数如下：

F=Fobj+Fp,

(19)

(20)

式中：λP、λV、λQ、λS分别为惩罚系数；ΔPG1、ΔVBi、ΔQGi、ΔSLi分别为平衡节点有功出力越限惩罚项、节点电压越限惩罚项、发电机无功出力越限惩罚项、支路容量越限惩罚项。对惩罚项的具体计算方法如下：

(21)

(22)

若在求解过程中出现越限问题,使用式(22)计算各惩罚项,否则各惩罚项均取0。

2 鲸鱼优化算法

鲸鱼优化算法是模拟座头鲸的泡泡网觅食方式发展而来的群智能优化算法[16]。该算法共包含3个阶段,分别为搜寻猎物、包围猎物和螺旋更新。座头鲸群首先通过搜寻猎物获取猎物的有关信息,然后以猎物为中心不断地螺旋上升,在上升的过程中同时吐出气泡,最后形成一个圆形的气幕大网,完成猎食行为,即找到问题的最优解。整个觅食过程如图1所示

图1 泡泡网觅食过程

2.1 搜寻猎物

假设整个种群中共有n条鲸鱼,搜索空间为d维,则所有鲸鱼在空间中的位置可以用矩阵表示为

(23)

在矩阵W中,每只鲸鱼的位置即对应问题的一个解,可以用Wi表示。在搜寻猎物阶段,由于鲸鱼无法及时获取猎物的任何信息,需要通过随机游走的方式不断搜寻猎物的线索。根据第t次的搜索行为,当|A|>1时,鲸鱼对第t+1次的搜索行为进行更新,此时的数学模型为

D=|CWrand(t)-Wi(t)|,

(24)

Wi(t+1)=Wrand(t)-AD,

(25)

式中：D为当前鲸鱼与猎物之间的距离；Wi(t)为当前鲸鱼的位置；Wrand(t)为群体内任意鲸鱼的位置；t为当前迭代的次数；A和C分别为系数向量,即

A=2ar1-a,

(26)

C=2r2,

(27)

式中：r1,2∈[0,1]；a为控制参数,即

(28)

式中：tmax_iter为设定的最大迭代次数。

2.2 包围猎物

式(28)中,控制参数a随着迭代次数的增加,从2线性递减到0,此时系数向量A也相应地减小,当|A|≤1时,算法从搜寻猎物阶段进入包围猎物阶段。此时,猎物的位置即对应问题的全局最优解,包围猎物阶段的数学模型为

D=|CWp(t)-Wi(t)|,

(29)

Wi(t+1)=Wp(t)-AD,

(30)

式中Wp(t)为猎物位置,即全局最优解。

2.3 螺旋更新

座头鲸在进行泡泡网觅食时,以猎物为中心不断地螺旋上升,在上升过程中同时吐出气泡,最终形成一个圆形的气幕大网,完成猎食行为。模拟鲸鱼螺旋更新阶段的数学模型为

Wi(t+1)=D′eblcos(2πl)+Wp(t),

(31)

式中：b为对数螺旋线的形状参数,文中取1；l为[-1,1]的随机数；D′表示当前鲸鱼的位置和猎物位置之间的距离,即

D′=|Wp(t)-Wi(t)|。

(32)

由于座头鲸捕食过程需要实现包围猎物和螺线更新2个阶段同时进行,为了模拟这种行为,设置随机概率p对位置更新策略进行选择,p为0～1的随机数,具体的数学模型为

(33)

3 改进的鲸鱼优化算法

在电力、机械等实际工程中,由于求解的大多数为高维问题,目标函数复杂,且需要考虑多种约束,基本的鲸鱼优化算法仍然存在着求解精度低、收敛速度慢等缺点。

文献[19]提出从种群初始化、位置更新以及预防陷入局部最优3个方面改进WOA算法,使用了准反向学习初始化种群、自适应权值策略和差分变异策略。

文献[21]提出用Levy飞行学习策略替代算法中的螺旋更新阶段,加强算法的搜索能力。

现有文献中,对WOA算法的改进大多数都是从调整参数入手,通过改进算法中的部分参数来达到平衡全局搜索和局部开发能力。而最优潮流问题的目标函数复杂,极值多,针对这样一个非线性非凸优化问题仅调整参数无法达到预期的寻优效果,因此提出一种平均群改进鲸鱼优化算法(average swarm improved whale optimization algorithm,AWOA)。在AWOA算法中,通过加入一个新的数学模型强化搜寻、包围猎物阶段的搜索能力,同时结合适用于其他非凸优化问题的非线性收敛因子和Levy飞行策略,平衡算法的全局搜索和局部开发能力,帮助算法跳出局部最优。

3.1 平均群模型

由式(24)、(29)可以看出,在WOA算法的搜寻、包围猎物阶段,任意鲸鱼位置Wrand和系数向量C起到关键性作用。随着迭代的不断进行,任意鲸鱼位置Wrand能够为算法提供全局随机寻优,系数向量C能够帮助算法跳出局部最优。然而最优潮流问题的变量多,目标函数较为复杂,使用WOA算法求解时,任意鲸鱼位置Wrand和系数向量C由于随机性太强,在寻优过程中能够起到的作用不大。为了强化算法的搜索阶段,提出一种新的数学模型：

(34)

D=|Wavg,d-Wd|,

(35)

式中：Wid为各维度下鲸鱼种群的位置向量；n为初始设置的种群数量；d为问题的维度。

平均群模型寻优流程如图2所示。根据式(34)中鲸鱼种群的位置向量Wid,计算每一维度,即每个变量的平均值,得到一个d维的群平均值向量Wavg,d。然后,计算所有个体向量到群平均值向量Wavg,d的距离矩阵D。最后,用式(35)替换式(26)、(31),其余步骤按原WOA算法进行。平均群模型能够驱使种群中的每条鲸鱼都参与后续迭代,在平均值范围附近进行位置更新,针对最优潮流问题使用该模型,能够避免在搜寻、包围猎物阶段不断的从种群矩阵W中随机寻找个体鲸鱼,有效提升算法的全局搜索能力。

图2 平均群模型寻优流程

3.2 非线性收敛因子

系数向量A是WOA算法中调整全局搜索和局部开发的重要因素,主要通过收敛因子a计算得到。由式(28)可知,收敛因子a随迭代次数的增加呈线性递减,使得算法无法有效平衡全局搜索和局部开发能力,因此提出一种余弦型非线性收敛因子，

(36)

图3为非线性收敛因子迭代至200次时的示意图。

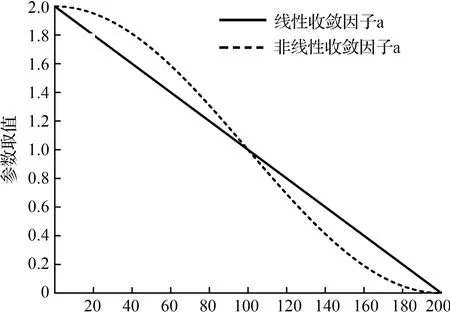
迭代次数

由图可见,在前100次迭代中,所提出的余弦型收敛因子增大以提高算法前期的全局搜索能力。随着算法的不断进行,当进入到后100次迭代时,余弦型收敛因子相应减小,这样可以细化算法后期的局部搜索,提高算法的局部开发能力。

3.3 Levy飞行策略

Levy飞行作为一种随机搜索方式,在多种智能算法的非凸优化问题上得到了运用。采用Levy飞行策略,利用随机步长于当前最优位置附近进行小范围搜索,在算法每次迭代后再额外迭代1次,扩大算法的搜索范围,有效帮助算法跳出局部最优。Levy飞行位置更新的数学模型为

Wp(t+1)=Wp(t)+α⊕Levy(β),

(37)

式中：α为步长尺度系数,文中取0.01；⊕为点积；Levy(β)为飞行分布下的随机步长,

(38)

式中：β为0到2之间的常数,文中取1.5；u～N(0,σ2)；v～N(0,1)；σ的计算公式为

(39)

式中,Γ(x)为Gamma函数,即Γ(x)=(1-x)!。

4 AWOA算法流程

AWOA算法求解最优潮流的具体步骤如下:

Step1:电力系统初始化。输入系统的节点和线路参数、发电机有功出力、节点电压幅值、变压器变比和无功补偿器功率上下限。

Step2:将含不等式约束的非线性最优潮流规划问题转化为带惩罚项的无约束规划问题,如式(19)所示,等式约束满足基本的潮流方程。

Step3:AWOA算法初始化,设置最优潮流的控制变量维度d、鲸鱼种群数量n、最大迭代次数tmax_iter和对数螺旋线的形状参数b。

Step4:在搜寻、包围猎物阶段使用平均群模型,用式(35)替代式(26)、(31),同时结合非线性收敛因子。当p<0.5时,若|A|≤1,选择式(30)更新个体位置；当|A|>1,选择式(25)更新个体位置；当p≥0.5时,选择式(31)更新个体位置。通过不断迭代更新种群位置矩阵,计算每次的适应度值并选取最优解。

Step5:在迭代的过程中,针对每次迭代的最优解,采用Levy飞行策略即式(37)进行小范围搜索,并对比搜索前后的适应度值,得到4个目标函数的全局最优值。

Step6:输出全局最优值下各控制变量的具体结果。

AWOA算法流程如图4所示。

图4 AWOA算法流程

5 算例分析

5.1 优化结果分析

为了检验改进后的AWOA算法是否有效,采用IEEE30节点系统求解最优潮流问题。该系统共包含6台发电机组、4台变压器和41条支路。文中待求的控制变量共有24个,包含5个发电机的有功出力(平衡节点除外)、6个发电机母线电压幅值、4个变压器变比以及9个无功补偿装置。

为了方便与现有文献给出的结果进行比较,假设变压器变比和无功补偿容量均为连续可调变量。

IEEE30节点系统的接线图和各项参数参见文献[22]。

仿真实验采用MATLAB R2018a软件进行,将AWOA算法的鲸鱼数量设置为30,tmax_iter设置为200,求解文中4个目标函数,得到各目标的全局最优解和控制变量的结果见表1。

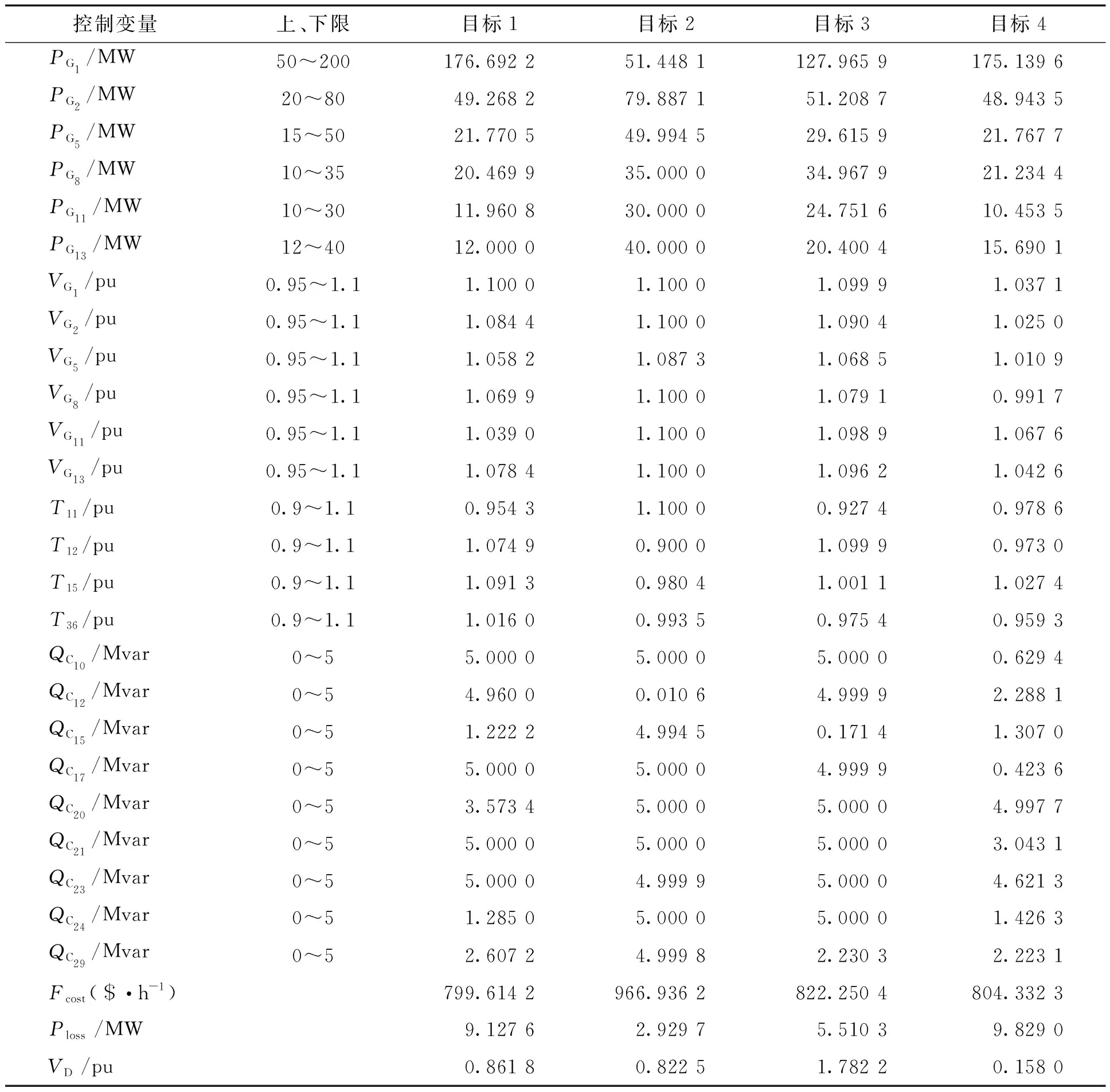
表1 AWOA算法的最优潮流计算结果

由文献[10]可知,在优化前,系统的初始发电成本为901.88 $/h,初始系统网络损耗为5.608 MW,节点电压偏移为1.155 4 pu。对目标1使用AWOA算法优化后,发电成本下降为799.614 2 $/h,节约了11.34%的发电费用。对目标2优化后,网络损耗下降为2.929 7 MW,降损约为47.76%。目标3同时考虑了发电成本和网络损耗,对目标3优化后,发电成本下降为822.250 4 $/h,网络损耗下降为5.510 3 MW,做到节约发电成本时保证网络损耗最小。目标4同时考虑了发电成本和电压偏移,对目标4优化后,发电成本下降为804.332 3 $/h,并且节点电压始终维持在1.0 pu左右,在节约发电成本的基础上保证了电压质量,电压偏移指标远小于前面3种情况。

5.2 算法对比分析

5.2.1 改进前后对比

为了体现AWOA算法的优势,选取以上4个目标为适应度函数,鲸鱼数量设置为30,tmax_iter设置为200,其他参数保持一致,分别计算30次,得到改进前后的数据统计和平均计算耗时比较见表2。

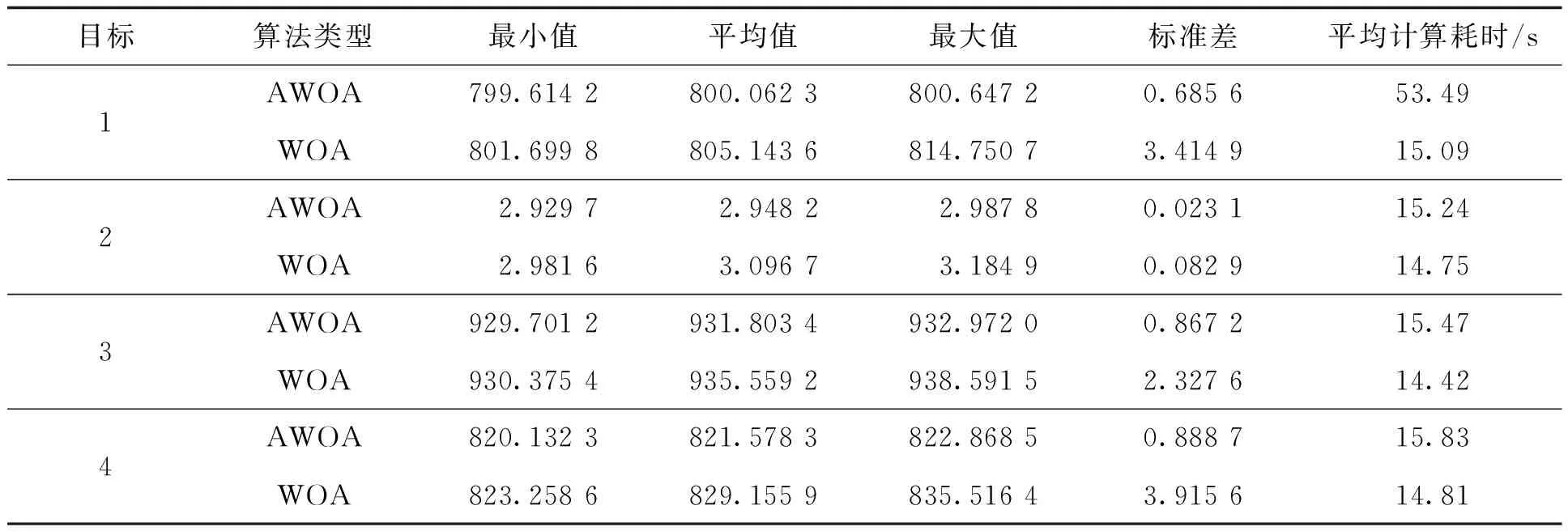
表2 改进前后的数据统计和平均计算耗时比较

由表可知,改进后的AWOA算法虽然在平均计算耗时上有所增加,但是可以搜寻到更小的目标值,并且综合这30次迭代优化可以发现,AWOA算法的标准差更小,说明改进后算法的性能更加稳定,在平衡收敛速度和求解精度方面具有显著优势。为了直观地展现改进前后算法的寻优过程,选取表2中4个目标函数的最小适应度值作收敛曲线,如图5—8所示。

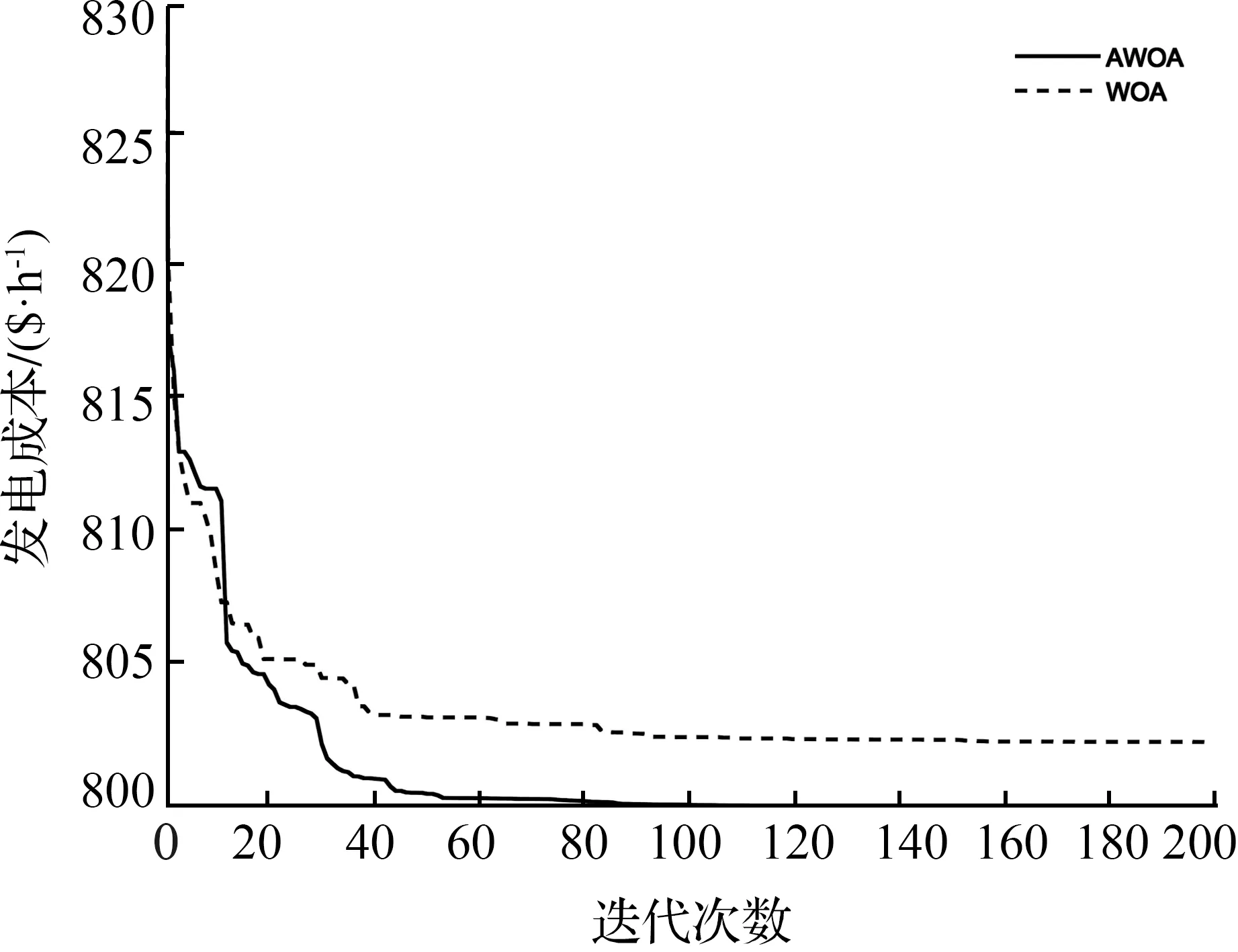
图5 目标1收敛曲线

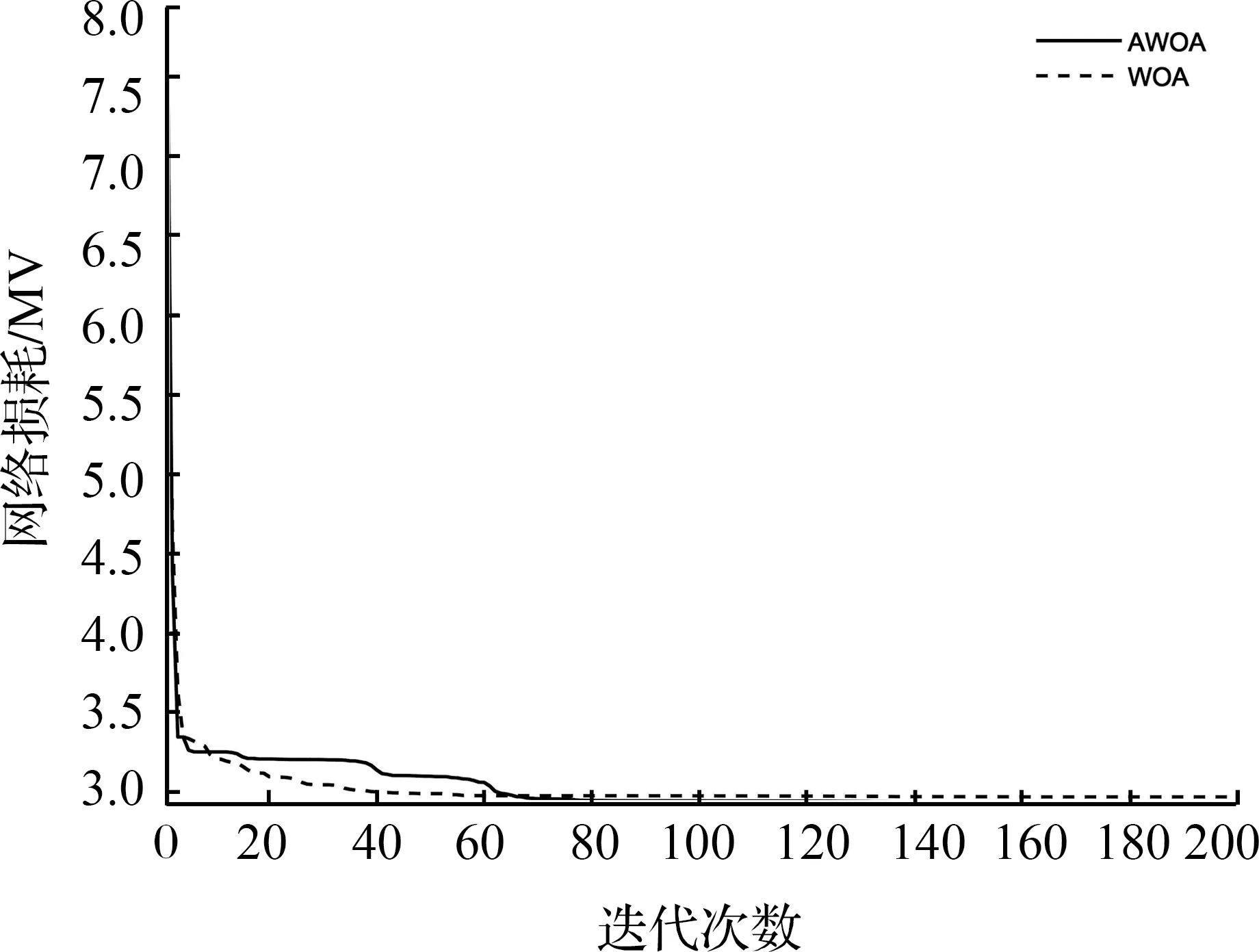
图6 目标2收敛曲线

图7 目标3收敛曲线

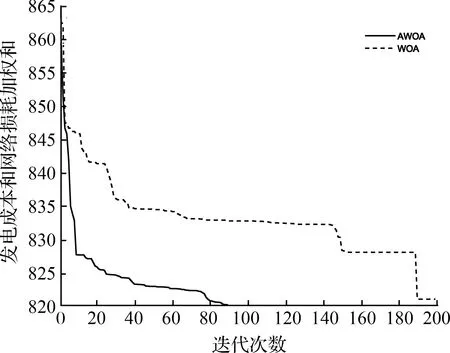
图8 目标4收敛曲线

从以上4图中可以明显看出,AWOA算法收敛速度更快,在迭代次数为40～80时收敛至最小值,并且收敛性能更加稳定。仅对比收敛曲线,无法直观地看出改进后算法在寻优过程中的优势,因此选择图5中的目标一收敛曲线,记录下每次迭代的最优位置,将最优位置的第1、2、3维(1号、2号、5号发电机的有功出力)映射至三维坐标系中作个体位置分布图,如图9、10所示。

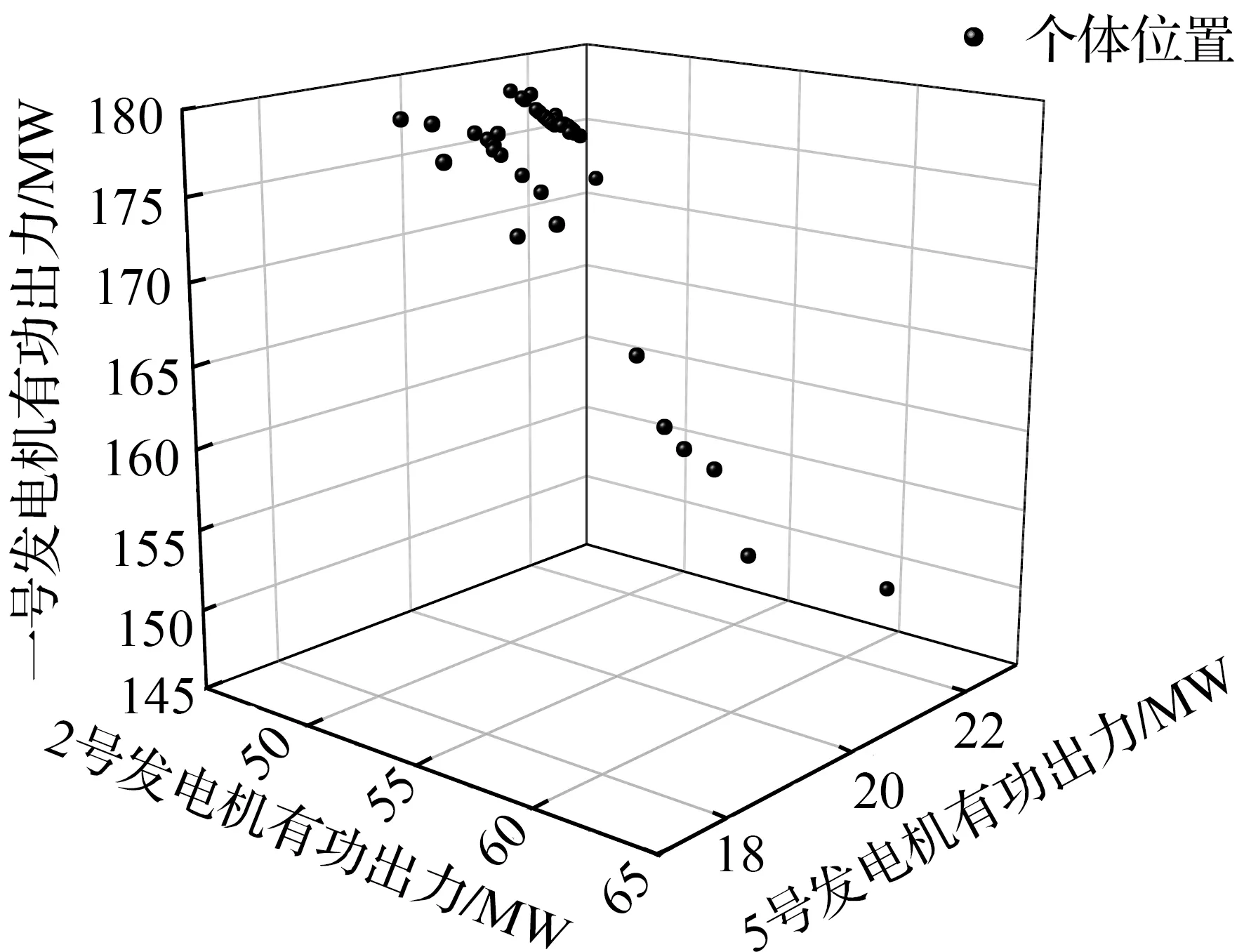
图9 WOA个体位置分布

图9中,WOA个体位置分布松散,且可以观察到,在200次迭代过程中,出现了较多重复位置,说明算法易陷入局部最优,整体寻优能力较差。而图10中,AWOA个体位置分布紧密且重复位置较少,算法可以围绕最优解进行细致搜寻,后期能够有效跳出局部最优。

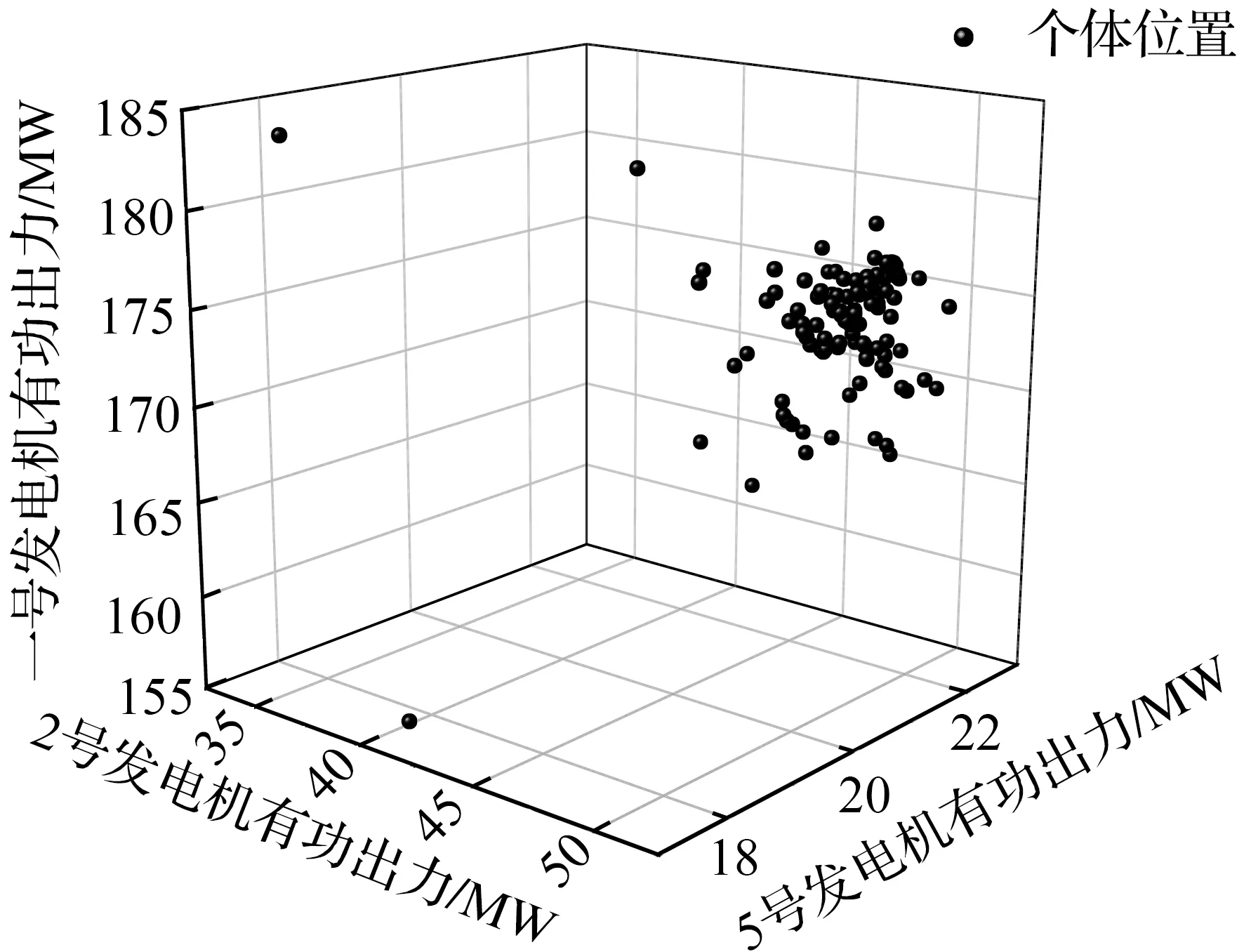
图10 AWOA个体位置分布

经过上述平均计算耗时、收敛曲线和个体位置分布的对比,可以得出改进后的AWOA算法虽然在计算时间上有所增加,但是收敛速度快，寻优精度高,而且在迭代过程中能够在最优解附近进行小范围搜索,跳出局部最优的能力强。

5.2.2 其他算法对比

由于仅对比WOA算法,无法充分说明改进后算法的优势,因此增加PSO、ABC、MFO3种智能优化算法和AWOA算法作比较。选取目标1为适应度函数,各智能算法的最大迭代次数均设置为200,种群数量设置为30,分别计算30次,并选择其中最小的适应度值作收敛曲线,各算法的收敛曲线如图11所示。

图11 各算法目标一收敛曲线

从图中可见,AWOA算法的初始值较小,并且在迭代前期的下降速度最快,能够搜寻到比PSO、ABC、MFO等智能优化算法更小的发电成本,有效提升了算法的求解精度。

选取文中4个目标为适应度函数,进一步求得改进前后AWOA算法的最优潮流优化值,并和现有文献中其他智能优化算法比较,得到的详细数据见表3。

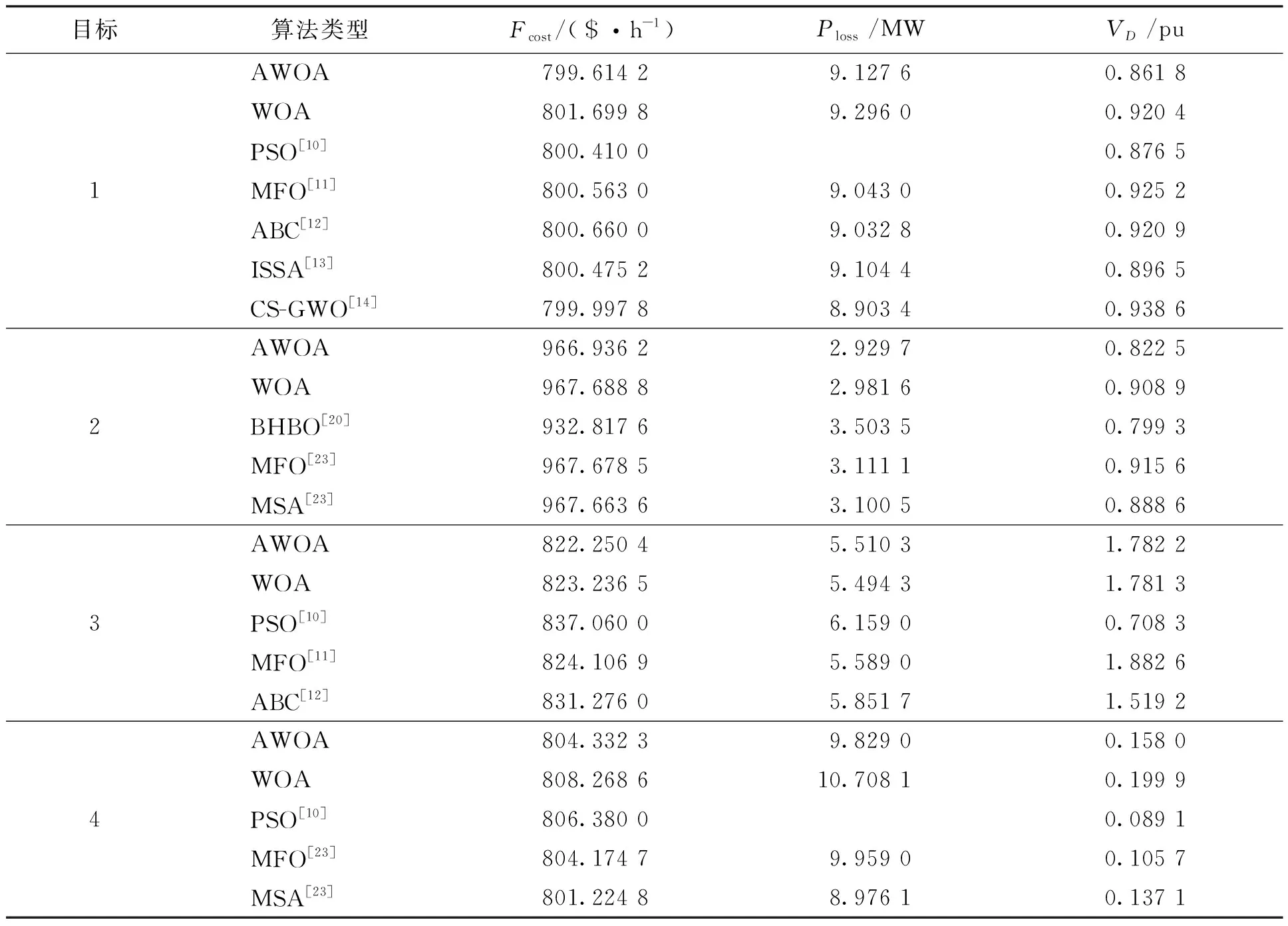
表3 不同算法仿真结果比较

通过观察图11中的收敛曲线和表3中的仿真结果,可以得出AWOA算法在求解电力系统最优潮流这类复杂问题时,能够在多约束条件下搜寻到更理想的目标值,与其他智能优化算法相比,具有为明显的优势。

6 结语

本文中提出了一种基于平均群改进鲸鱼优化算法(AWOA)的最优潮流计算。针对鲸鱼优化算法在求解高维、复杂问题时易陷入局部最优的缺点,采用平均群模型并结合非线性收敛因子、Levy飞行策略对算法进行改进。在IEEE30节点系统下对改进后的算法进行验证,结果表明AWOA算法的收敛速度更快且寻优精度更高,在求解最优潮流问题时具有明显优势。接下来的工作是研究多目标的最优潮流计算以及概率潮流计算。