综合测量纺织面料的红外发射率及光热吸收率

陈益松，张 悦

(东华大学 a.服装与艺术设计学院；b.现代服装设计与技术教育部重点实验室，上海 200051)

红外发射率和光热吸收率是物体的两个重要热学指标。红外发射率是标识物体向外辐射红外波段能量的指标，光热吸收率是标识物体在可见光波段和红外波段对外界辐射能吸收能力的指标，两者虽不相同却又相互联系。自然界的物体都会向外界辐射红外光谱，同时也吸收来自外界的光热辐射。纺织面料作为服装的主要构成材料，夏季需要其光热吸收率越低越好，而冬季相反。纺织面料在隐身领域，其红外发射率则越小越好；而在海水淡化领域则需要覆盖海水面料的光热吸收率通常越高越好。因此，有效测量面料的红外发射率和光热吸收率是十分重要的。

红外发射率可以使用以反射率法为基础的光谱仪进行测量[1]，但全谱光谱仪价格昂贵、操作复杂并不普及。相对独立的红外发射率测量方法也有多种，其中以反射率法为基础研制的IR-2型红外发射率仪得到了广泛应用[2-3]。反射率法是通过瞬间曝光进行测量的，在实际测量过程中还需考虑未曝光时热源的影响。量热法或能量比较法也是测量红外发射率的常用方法，如Zhang等[4]使用黑体炉和辐射计对面料的发射率进行了测量，但试验过程中面料存在透射以及面料内外表面温度不相等都会导致测量误差。徐军等[5]则使用热板仪测量面料的热阻，并通过反算的方式获得红外发射率，解决了真实温度测量的问题，但依然存在透射的不良影响。陈益松等[6]将反射率法和量热法相结合开发了测量面料红外发射率的新装置和方法，能准确测量真实温度且避免了透射的影响，然而这种测量以红外传感器为基础建立辐射平衡关系，在概念上都局限在红外计量仪所在的8～14 μm波段内，并没有解决全谱段红外发射率的测量问题。全谱段红外平均发射率在工程热学计算更具有实际意义。

光热吸收率也可以使用光谱仪进行测量[7]，文献 [8-10]使用光谱仪测量了织物的光热吸收率。但除使用光谱仪之外的其他相对独立的测量方法还未有报道。

纵观上述，面料的红外发射率及光热吸收率在测量原理和测量方法方面的研究相对匮乏，本文依据光热辐射及相关传热学的基本原理，探索了常规实验室条件下全谱段红外平均发射率和光热吸收率的新测量方法，并结合自制的试验装置，对一组面料进行了测量并得到了可信的结果。

1 光谱分布与光谱仪

太阳辐射光谱能量主要集中于可见光(波长为0.36～0.72 μm)和近红外区(波长为0.72～2.50 μm)[11-12]。根据普朗克定律，通常物体于0～50 ℃下的常温热辐射能量主要体现在中远红外波段(能量95%分布在波长为5.00～60.00 μm)。物体在吸收外部的光热辐射后，内能增加并温度升高，同时以中远红外辐射的方式释放部分能量。

全光谱光热吸收率是所有光谱段上吸收的能量与投射到物体上全部光谱的能量之比，通常是在0.3～2.5 μm可见光波段和红外波段进行的[13]。利用光谱仪在全波段测量物体表面的反射率和透射率来计算全光谱光热吸收率(β)；在被测物体为灰体且检测波段为红外波段时，红外发射率等于红外吸收率，因此，只需对红外波段进行积分就可以得到物体的红外发射率[1]：

(1)

式中：λ为光谱波长;λmax为光谱最大波长;λmin为光谱最小波长；R(λ)为光谱反射率分布；T(λ)为光谱透射率分布；G(λ)为光谱入射强度分布。

虽然在测量原理上红外发射率和光热吸收率都可以通过全谱光谱仪实现，但光敏传感器的频谱响应范围通常是有限的，不能广域兼顾可见光到远红外光谱，需要多种规格的传感器联合工作。因此，能够全光谱测量的光谱仪是复杂且昂贵的，应用并不普及。

2 新测量原理

采用外部光热辐射源对贴于绝热装置的面料进行辐射加热，由于面料背面方向绝热，面料温度升高只会向正面方向辐射红外线，并与环境空气发生对流达到热平衡，通过测量面料的真实温度、有效辐射温度以及相应的环境温度，可以计算出面料相应谱段的平均红外发射率和光热吸收率。

2.1 红外发射率测量

光线在纺织面料表面一般呈漫反射状态。因此面料归属于物理学“灰体”，而灰体的红外发射率等于红外吸收率[14]。当不考虑面料的透射时，则：

ρ=1-δ=1-ε

(2)

式中：ρ为面料的红外反射率；δ为面料的红外吸收率；ε为面料的红外发射率。

当测量装置放置在一个恒温环境箱内，由于近距离测量，可以忽略空气本身的影响，根据辐射能守恒定律，则面料向外有效辐射能计算如式(3)所示[15]。

(3)

式中：Er为面料向外的有效辐射能(即外界所能检测到的辐射能)，W/m2；σ为黑体辐射常数，5.67×10-8W/(m2·K4)；Tr为面料的有效辐射温度，K；Tf为面料的实际温度，K；Ta为环境温度，K。

将式(2)和(3)变换，就得到面料表面的红外发射率计算如式(4)所示。

(4)

式(3)与(4)是建立在整个红外波段上的，其能够实现全波段红外发射率的测量。虽然在形式上与文献[6]的公式相同，但物理含义是不同的。

2.2 光热吸收率测量

根据物理定义，面料的光热吸收率β计算方法如式(5)所示。

(5)

式中：Qf为面料吸收的光热辐射量，W；Qin为入射光照量，W。

黑体则是一种理想化的物体，其没有任何的反射与透射，能吸收外来的全部电磁辐射，即黑体吸收的光热辐射量为入射光照量。以黑体作为参考标准进行比较，面料的光热吸收率计算如式(6)所示。

(6)

式中：Qb为黑体吸收的光热辐射量，W。

直接测量面料和黑体吸收的光热辐射量较为困难，但面料吸收光热辐射后通常会转换为能量储备，从而使自身的温度升高，同时面料也会向外界散失更多的热量。当面料与外界环境达到热平衡时，面料吸收的光热辐射量则为与外界对流和向外热辐射散失的热量(即非静态空气热传导基本不存在)，如式(7)所示。

Qf=Qc+Qr

(7)

式中：Qc为以热对流传递的热量，W；Qr为面料向外环境的热辐射量，W。

如果面料正面接受光热辐射而其背向绝热，则沿面料正面竖直方向上的自然对流传热热量为

Qc=hA(Tf-Ta)

(8)

式中：h为自然对流传热系数，W/(m2·K)；A为传热面积，m2。

在试验中，面料试样的面积相较于实验室内空间表面的面积小很多，故面料与室内空间表面的相互辐射传热可简化为式(9)[15]：

(9)

面料在吸热和放热平衡条件下，将面料光热吸收率的计算式改写为式(10)。

(10)

式中：Tb为黑体的表面温度，K。

将式(4)代入到式(10)则得：

(11)

2.3 黑体温度Tb的确定

在同一光热源辐射的情况下，黑体的表面温度可用黑漆铜板的表面温度换算得到。假设黑体和黑漆铜板在受到光热辐射后表面温度分别上升至Tb和T0，两者的关系可表示为

(12)

式中：ε0为黑漆铜板的红外发射率，公认数值为0.95[16]；E0为黑漆铜板的辐射功率，W/m2；Eb为黑体的辐射功率，W/m2；T0为黑漆铜板的表面温度，K。

将式(12)改写为式(13)，得到黑体的表面温度。

(13)

2.4 对流传热系数h的确定

在自然对流的情况下，用瑞利数Ra来判断空气的流动情况。当104≤Ra≤109时，空气的流动状态为层流；当109≤Ra≤1013，空气的流动状态为湍流。Ra计算方法如式(14)所示。

(14)

式中：g为重力加速度,g=9.8 m/s2；γ为热膨胀系数，对于理想气体，其数值为定性温度的倒数，K-1；l为特征长度，m；ν为运动黏度，m2/s；D为热扩散率，m2/s。

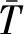
(15)

因为空气可看作理想气体，则热膨胀系数γ可表示为

(16)

在试验中，面料的特征长度l为0.30 m，Tf与Ta的温差为14.80～18.40 K。稳态下计算出的定性温度为301.25～302.65 K，则定性温度可取300.00 K，在该温度下空气的物性参数的具体情况如表1所示。

表1 温度300.00 K下空气的物性参数Table 1 Physical parameters of air at 300.00 K

根据式(14)计算出瑞利数Ra为3.65×107～4.54×107，空气流动状态为层流。对于垂直平板且空气流动为层流时，可根据努塞尔数Nu来计算对流系数h[18],如式(17)所示。

(17)

则根据式(17)可计算出对流传热系数h为3.56～3.76 W/(m·K)，本次试验中对流传热系数取3.60 W/(m·K)。

3 试验设计

3.1 试验装置构成

采用两盏功率为500 W的新闻碘钨灯作为光热辐射源，并使用稳压电源供电，以保证光热辐射功率的稳定性。灯色温约3 000 K，95%的辐射能量分布在波段0.55～5.50 μm，光热比例为3∶7，用来模拟与地面呈25°～45°夹角的太阳光照。面料温度为0～60 ℃，其向外辐射的95%能量集中在波段6～60 μm，与碘钨灯的辐射波段基本没有交集，即两者并不相互干扰。两盏灯呈60°夹角对面料进行辐射加热，可以使面料更均匀地接受光热辐射，同时也可以使红外热像仪(或测温枪)居中测量。热像仪通常检测的波段为8～14 μm，其主要感知面料常温波段的红外辐射，而对光热灯不敏感。因此试验采用IHT600型测温枪，分辨率为0.1 ℃，当内置发射率ε设置为1时，所测量温度则为面料的有效辐射温度Tr。

1—水银温度计； 2—面料； 3—KT板+泡沫板；4—光热辐射源； 5—红外测温仪或测温枪。图1 面料发射率的测量装置Fig.1 Fabric infrared emissivity measuring equipment

将面料直接贴附于由高反射率(白色)的KT板和泡沫板构成的近似“绝热”的装置上。KT板上制作凹槽用于放置水银温度计。KT板+泡沫板的厚度为3 cm，热阻实测为0.98 (m2·K)/W，是普通面料的50倍左右，由此可以认为相对于面料而言，KT板+泡沫板是“绝热”的。由于面料背面与“绝热”装置没有热流传递，面料正反面的温差为0，则面料后面的水银温度计测得的温度为面料正面的真实温度。水银温度计的量程为0～50 ℃，精度为-0.1～0.1 ℃。

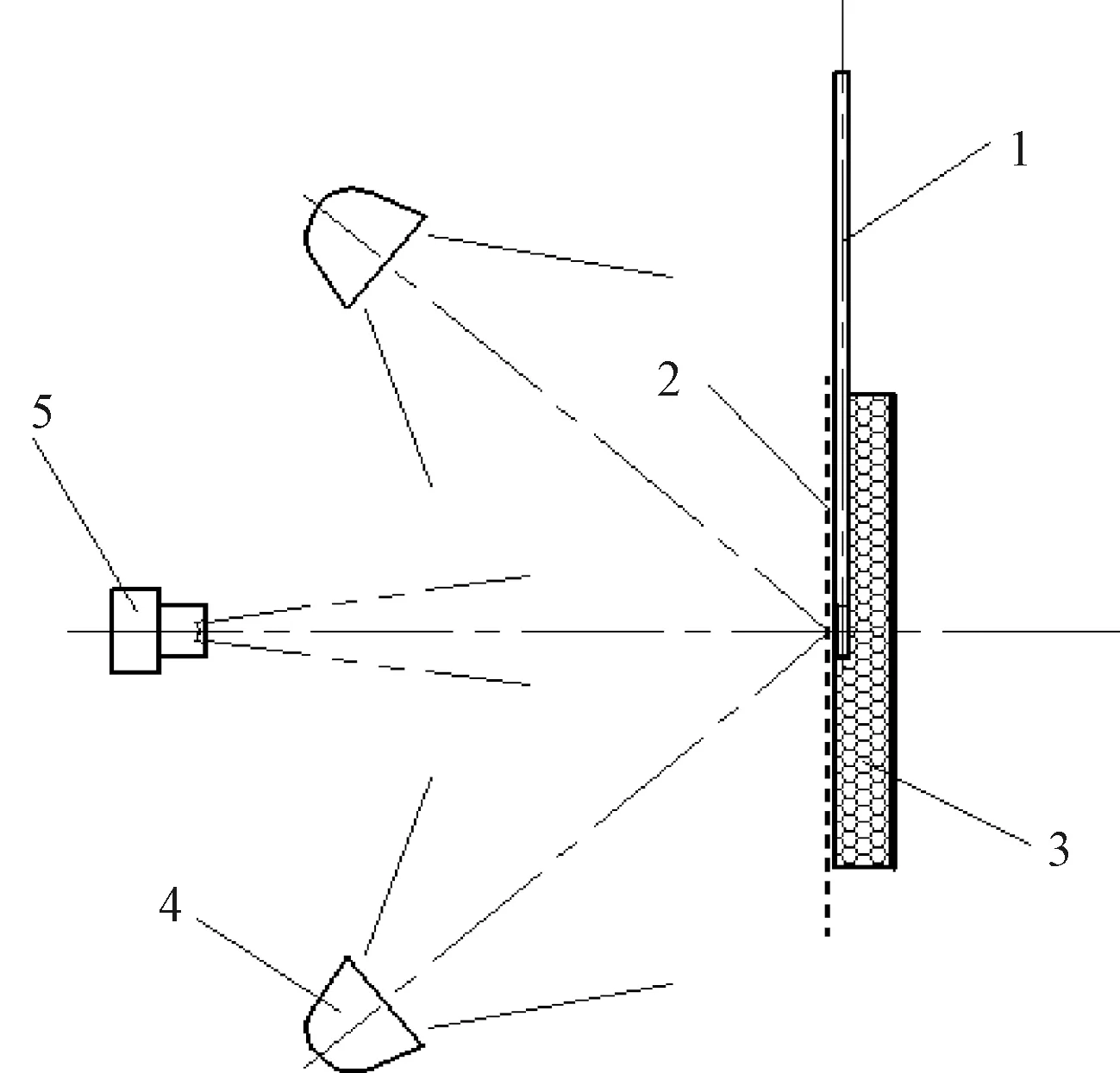
面料的光与红外线透射率为5%左右[4,19]。采用高反射率表面的KT板可使穿透面料的光热再次反射回面料，当反透射回的光和红外线再次透射的比例下降到0.25%或更少，可忽略此项影响。图2为试验红外热像图。由图2可知，红线位置为KT板及泡沫板隔热装置，面料吸收热量升温后呈深红色，而未覆盖面料部分KT板的温度基本和周边环境一致，这说明KT板对光热辐射的吸收率很低。

图2 试验红外图像Fig.2 Infrared image of the test

3.2 试验环境

本次试验均在恒温、恒湿的实验室中进行，试验环境参数如表2所示。

表2 试验环境参数设置Table 2 Test environment parameter setting

3.3 试验面料

试验面料选用了黑、紫、蓝、绿、红、黄(橙)、白等7种颜色的棉机织物、色丁织物和棉针织物，不同材质面料相应的色彩之间稍有差异。其中色丁织物因织造结构因素，其正面光滑，反光率高于反面。表3为试样成分及其组织结构。本次试验还将对黑漆铜板进行测量，从而计算得到黑体的光热吸收功率。

表3 试样成分和组织结构Table 3 Composition and structure of the samples

3.4 试验时长

通过预试验发现面料系统在试验30 min后即达到平衡且保持稳定，试验总时间为60 min，取后3次数据，求均值。试验过程中，各温度参数随时间变化的典型曲线如图3所示。

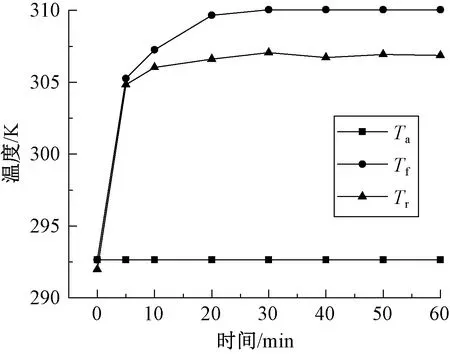
图3 各温度参数随时间变化的典型曲线Fig.3 Typical curve of each temperature parameter changing with time

4 结果与分析

在试验达到平衡后分别记录面料的有效辐射温度Tr和面料的真实温度Tf，其中，发射率为0.95的黑漆铜板的表面温度为318.25 K。根据式(13)计算黑体的表面温度为322.36 K。表4为试样的试验数据及相应的测算值。由表4可知，不同面料之间的光热吸收率和红外发射率均存在差异。

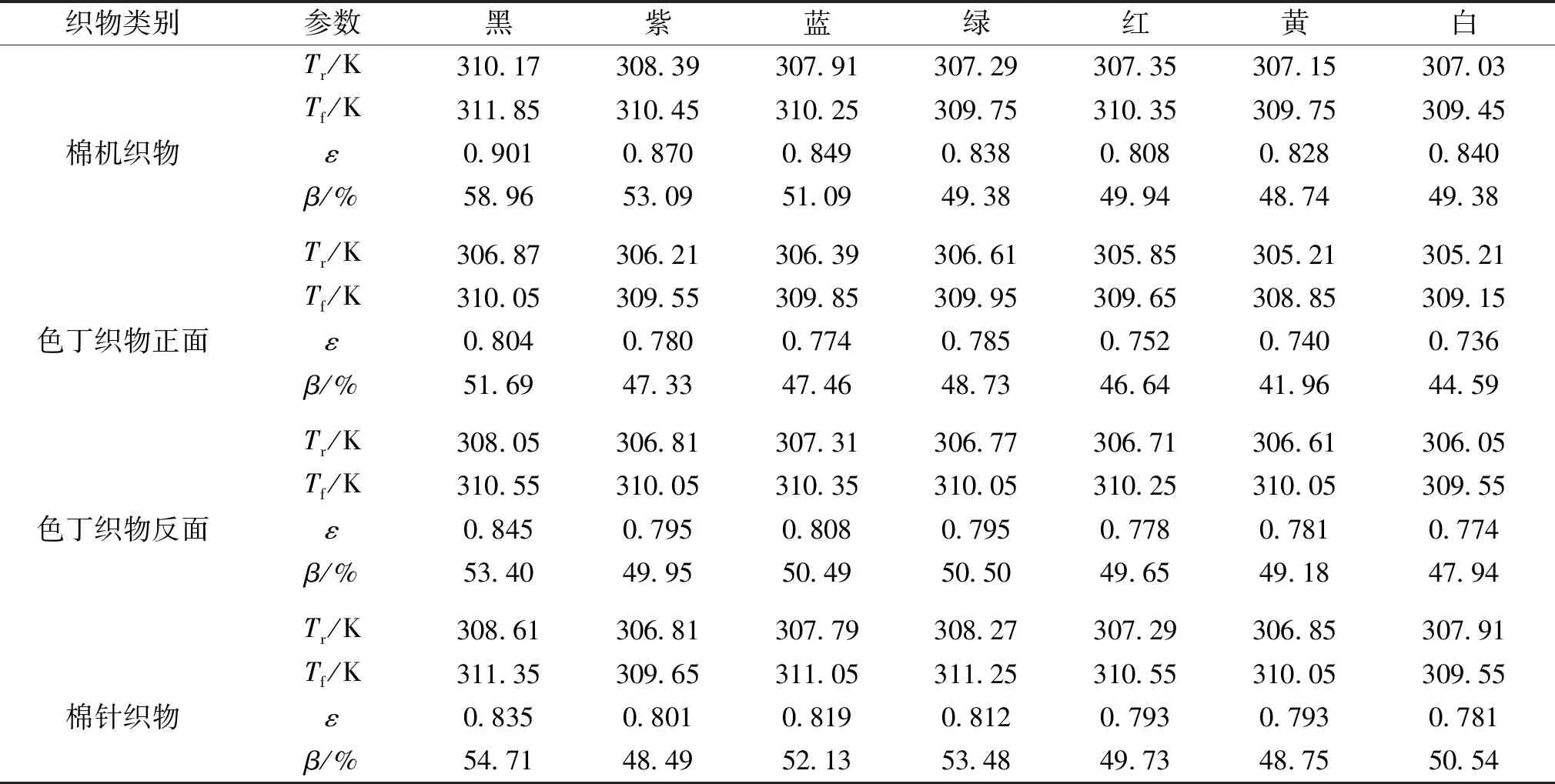
表4 试样的试验数据Table 4 Test data of specimens

试验面料的红外发射率为0.736～0.901，红外发射率由大到小的顺序为棉机织物>棉针织面料>色丁织物反面>色丁织物正面。其中，深色面料的红外发射率略高于浅色，但差异不大。

试验面料的光热吸收率为41.96%～58.96%，与文献[21]表明的无涂层面料的光热吸收率(40%～50%)基本相符，光热吸收率由大到小的顺序为棉机织物>棉针织物>色丁织物反面>色丁织物正面。其中，色丁织物正面的光热吸收率要小于反面，这是因为色丁织物组织结构的差异导致正面的光热反射能力高于反面。由此可知，面料正面吸收和透射热的能力较弱，其温度低，即光热吸收能力差。

为验证试验装置检测的可信度，本文对黑漆亚光铜板(漆面为高分子材料，按灰体来对待)、不锈钢板的红外发射率和光热吸收率进行了测量，结果如表5所示。由表5可知：亚光黑漆铜板的发射率约为0.934，与文献[20]中黑漆发射率0.880～0.960的参考值差别不大；不锈钢板(因久置而表面较暗淡)所测的发射率约为0.251，在0.170～0.300的参考值[20]范围内。亚光黑漆铜板的光热吸收率为80.74%，光面不锈钢板的光热吸收率为37.84%，两者数值差异明显要高于面料。由此可知，本文试验装置的检测结果具有较高可信度。

表5 参考物的试验数据Table 5 Test data of reference materials

总体而言，黑色面料的光热吸收率最高，而浅色(黄或白)的光热吸收率相对较低，中间一些颜色的光热吸收率差异不明显，这是因为在本次试验中光源的光热比为3∶7，可见光的占比较小。若今后试验采用高色温的光热源，即增加可见光的占比，则颜色间的光热吸收率差异会增大。

5 结 语

本文以单向传热为基础推演确立了纺织面料的红外发射率及光热吸收率的测量原理，并借助自制的试验装置，在一般实验室条件下实现了面料红外发射率和光热吸收率的同步测量。

试验面料的红外发射率为0.736～0.901，不同颜色的红外发射率差异不大。试验中面料的光热吸收率为41.96%～58.96%，与现有的无涂层织物光热吸收率的数据范围基本相符，深色面料的光热吸收率要高于浅色面料。利用自制的试验装置检测黑漆铜板和不锈钢板的红外发射率，测量结果与相关文献中的数据相符，且黑漆表面和抛光不锈钢面的光热吸收率间的差异远大于不同颜色面料间的差异，与实际情况相符，因此试验结果具有较高可信度。

此外，试验中所测的是全红外波段的平均红外发射率，与光热辐射源的光谱基本没有重合，即测量结果与所使用的光热辐射源的类型基本无关；但光热吸收率与光热辐射源频谱处于高度重合范围，即与辐射源光谱分布直接相关，使用不同色温的光热源会得到不同的结果。