源于课本 渗透素养——2021年武汉中考数学第21题评析

武前炜

(安徽省合肥一六八陶冲湖中学 230601)

作为学科知识的重要载体，教材的重要作用和基础地位不容置疑

.

在教学过程中，教师要正确使用教材，更要创造性地使用教材，在课本的基础上适时、适当、适度地进行延伸与发散，重视课本的本源性

.

中考试卷中一些关键位置的题目具有较强的思维发散性，决定着整张试卷的区分度，但是发散的“源头”往往来自课本，课本习题承担着帮助学生理解和掌握数学基本知识、形成和发展数学基本技能的重要功能，特别是一些经典例题、习题是十分有价值的教学资源，也是很多中考题源的根

.

重视经典习题的探究学习、改编，能很好地帮助学生整合知识、探索规律、形成方法、获得经验，从而发展思维，提升素养，达到“做一题、会一类、通一片”的高效追求

.

1 题目呈现

如图1，

AB

是⊙

O

的直径，

C

,

D

是⊙

O

上两点，点

C

是的中点，过点

C

作

AD

的垂线

.

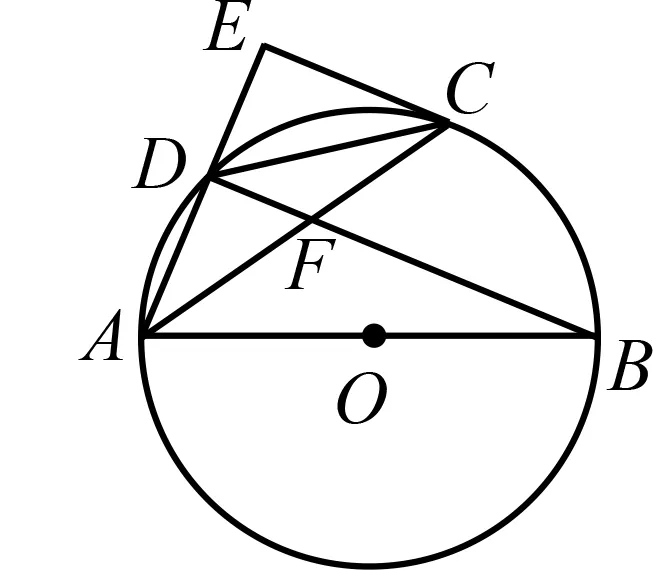
图1

(1)求证：

CE

是⊙

O

的切线；(2)若求cos∠

ABD

的值．本题为2021年湖北省武汉市中考数学第21题

.

2 追根溯源

本题以沪科版数学九年级下册第24章《圆》第69页第14题题干为基础，挖掘几何关系，可谓“根”在课本

.

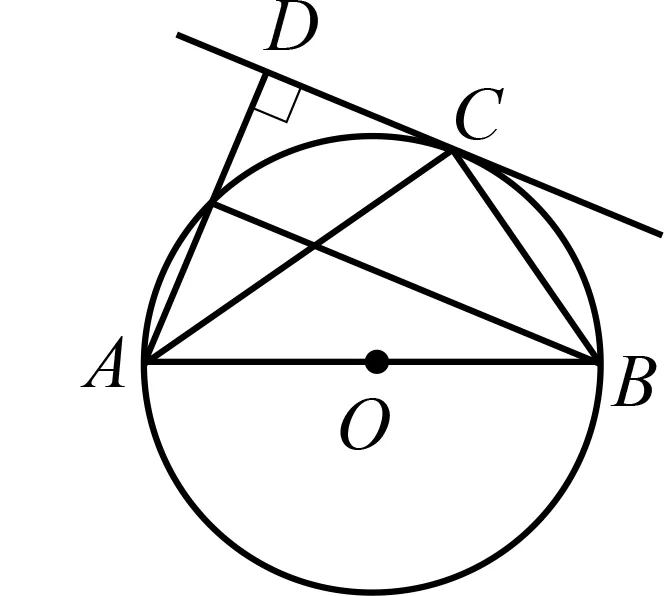
图2

(课本原题)已知：如图2，

AB

为⊙

O

的直径，点

C

在⊙

O

上，

AD

与过点

C

的切线垂直，垂足为

D.

求证：

AC

平分∠

DAB.

题目蕴含丰富的几何关系，比如圆周角定理、切线性质、垂径定理、角平分线性质、弦切角定理、三角形相似、圆内接四边形等，这些内容对锻炼学生的识图能力、辨析能力、推理能力以及转化意识都有重要的作用

.

正如叶圣陶所说：“教材只是个例子

.

”作为教师在教学中要依托课本习题，从不同的角度、不同的层面、不同的条件进行拓展研究，挖掘问题本质，帮助学生学会学习，强化知识理解与应用，发挥习题最大功效，从而帮助学生跳出“题海”

.

3 解法探究

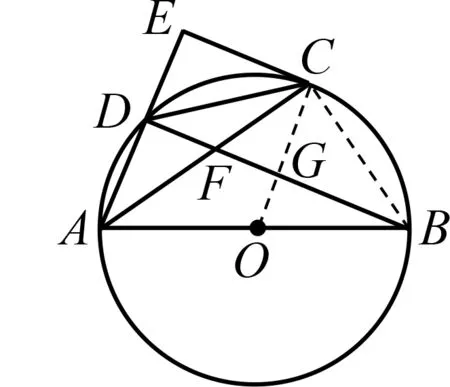
图3

分析 (1)如图3，连结

OC

交

BD

于点

G.

由

C

是的中点，可得

OC

⊥

BD

，且点

G

为

BD

中点

.

从而可得

OC

∥

AE

，于是

OC

⊥

EC

，即

CE

是⊙

O

的切线

.

(2)连结

BC

,由

C

是的中点，所以

CD

=

BC.

因为不妨设从而

解法1

(射影定理) 设

FG

=

a

，于是

BG

=

DG

=

a

+1

.

因为

AB

是⊙

O

的直径，于是∠

BCF

=90°

.

在Rt△

BCF

中，

BC

=

BG

·

BF

，即解得

a

=1(负值舍去)

.

于是可证△

ADF

≌△

CGF

(AAS)，从而

AD

=

CG.

由点

O

,

G

分别为

AB

,

BD

的中点，可知即在Rt△

BOG

中，可知

解法2

(相似) 因为点

C

是的中点，根据圆周角定理可得∠

DAC

=∠

CDF

,于是△

CDF

∽△

CAD

，于是不妨设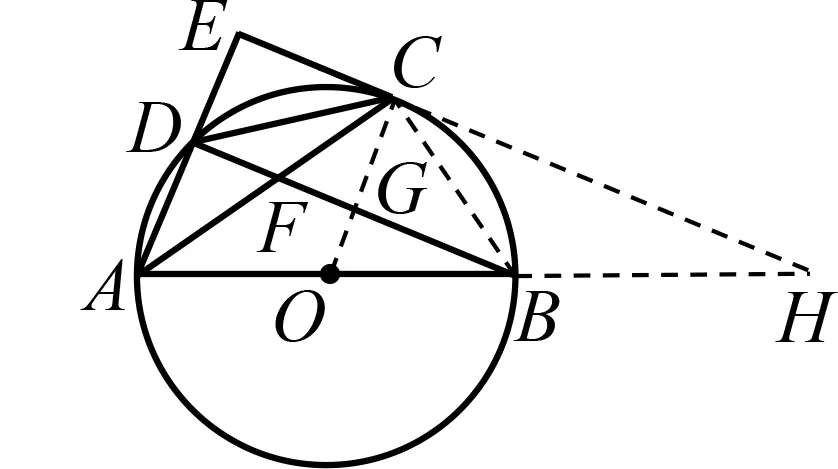

图4

如图4，延长

AB

,

EC

交于点

H.

因为∠

ADC

=∠

ADB

+∠

BDC

=90°+∠

BDC

,∠

ACH

=∠

OCH

+∠

ACO

=90°+∠

ACO

,而∠

ACO

=∠

OAC

=∠

BDC

,于是∠

ADC

=∠

ACH

,所以△

ADC

∽△

ACH

，则

AC

=

AD

·

AH

，解得

AH

=6

.

设⊙

O

半径为

r

，则

OA

=

OB

=

OC

=

r

，由△

ADB

∽△

OCH

,可得即解得(负值舍去)

.

在Rt△

ABD

中，可知

解法3

(相似+勾股定理) 由

BD

∥

EC

，可知∠

ECD

=∠

CDB

,而点

C

是的中点，于是可得∠

ECD

=∠

EAC

，从而△

ECD

∽△

EAC

，于是

EC

=

ED

·

EA.

设

EC

=

a

,

ED

=

b

，则

a

=

b

·(

b

+1)

.

由解法2知不妨设

AD

=1，在Rt△

ACE

中，由勾股定理得

AC

=

AE

+

EC

,即解得于是

CG

=

ED

=1

.

由点

O

,

G

分别为

AB

,

BD

的中点，可知即在Rt△

BOG

中，可知

4 解后反思

本题源自一道有价值的课本习题

.

图形中蕴含丰富的内涵，如“题目中的三个论断：①

CE

⊥

AD

；②

CE

是⊙

O

切线；③点

C

是的中点，可知二推一”、根据圆的性质导出等角产生很多相似结构、四边形

ABCD

为对角互补且邻边

BC

=

CD

具有旋转结构、

AC

平分∠

DAB

具有对称结构

.

通过图形结构剖析，对培养学生思维的发散性和灵活性十分有益

.

备考阶段，选取有价值的素材，展开全面研究，引导学生研究试题的“内涵”、解法、变式以及推广，构建知识链条，形成知识体系，落实核心素养

.

本题求解中条件在使用中可以根据需要利用等线段或者相似比灵活转化，而问题求解的余弦值实质上也是比值关系，为了简化运算假设这里条件的比值为什么是？能不能换成别的比值？

不妨设于是可得不妨设

AC

=

λ

,

AD

=1

.

设

EC

=

a

,

ED

=

b

，则

a

=

b

·(

b

+1)

.

在Rt△

ACE

中，由勾股定理得

AC

=

AE

+

EC

,即

λ

=(

b

+1)+

a

，整理可得2

b

+3

b

+1-

λ

=0，解得(负值舍去)

.

于是即

在Rt△

ABD

中，

若可知

若可知(即为本题结果)，

若可知

若可知

以上得出的值与sin∠

ABD

的一般关系，命题者命制该题时给出特殊比值使得sin∠

ABD

便于计算

.

这里在由比值推导三角函数值时，过程是可逆的，于是题目也可以改编为逆向考查：给出

sin∠

ABD

的值，求解的值

.

巧合的是，2021年四川自贡市中考数学第25题就是这样的命题思路

.

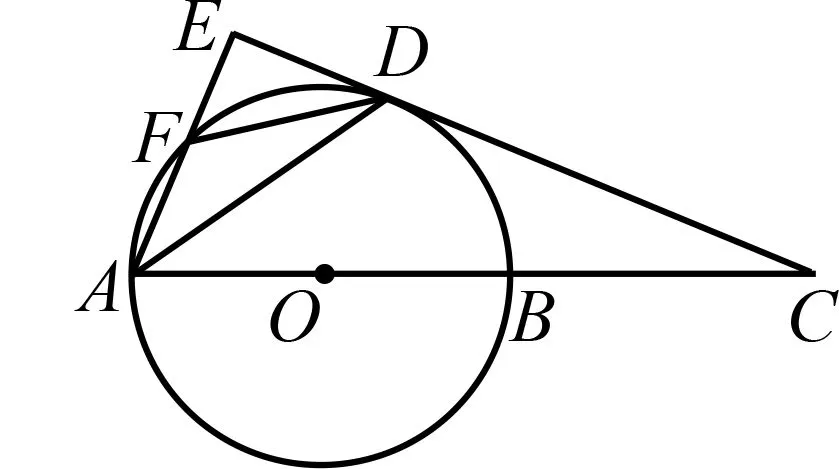
图5

(2021年四川自贡卷)如图5，点

D

在以

AB

为直径的⊙

O

上，过

D

作⊙

O

的切线交

AB

延长线于点

C

，

AE

⊥

CD

于点

E

，交⊙

O

于点

F

，连结

AD

,

FD

．(1)求证：∠

DAE

=∠

DAC

；(2)求证：

DF

·

AC

=

AD

·

DC

；(3)若求

EF

的长．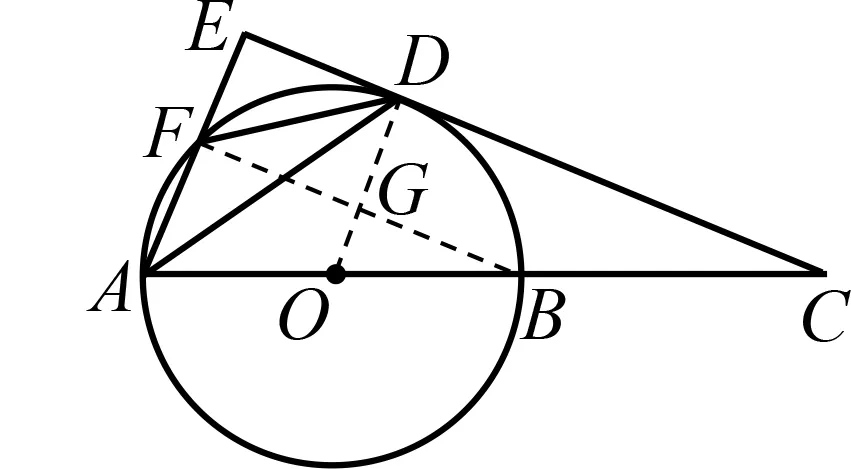

图6

简析

(3)如图6，连结

BF

，可知

BF

∥

CE

，于是∠

ABF

=∠

C

，则sin∠

ABF

由上述推广可知,于是由可知

AF

=4

.

从而可得从而

EF

=

DG

=

OD

-

OG

=6

.

具体解法留给读者探索，这里从略

.

5 教学启示

双减背景下，切实减轻学生负担要从教师“增压”开始，教材是教师教学和学生学习的“根”，教材中的习题是编写者精心设计的，值得教师深入研读、研究

.

我们注意到，很多中考题都是课本经典习题的改编和重组，也就是从课本的“根”生长出来的

.

用好教材、挖掘教材是教师专业基本功的重要体现，依托课本素材进行深入研究、变化，通过问题不同角度思考及变式训练培育学生核心素养

.

因此，要注重典型例题和习题延拓与发散，发展学生的思维、落实核心素养，积累活动经验，从而提高教学效率！