极限思想在高中数学中的运用——以圆锥曲线为例

姚 婷 吴如光

(南京师范大学附属中学秦淮科技高中 210003)

1 背景分析

极限对于学生来说并不陌生，小学阶段对于无穷大的数的感悟，初中阶段对于反比例函数图象的探究，高中阶段对于加速度概念的理解，无一不渗透着极限思想．章建跃博士在文[1]中指出：“在中学阶段,掌握一些微积分的初步知识,对发展学生的理性思维、增强数学应用能力等都是非常有用的．”极限思想是一种重要的数学思想，虽然高中数学教材中没有明确极限的概念，但极限思想却始终贯穿着高中数学的学习，以导数为典型，解析几何、立体几何、数列、三角函数等内容的学习过程中也绕不开极限．虽然高等数学中用“

ε

-

δ

”语言表述的极限定义对于中学生来讲难以接受，但是极限思想却是可以在学习中不断渗透的．利用极限思想，往往可以引导解题方向、规避复杂运算、突破解题难点．本文将结合圆锥曲线谈谈极限思想在高中数学中的运用．

2 引例分析

近日，笔者在教学中遇到这样一道解析几何综合题：已知点是椭圆上一点，

F

，

F

分别是椭圆的左、右焦点，

PF

+

PF

=4．设直线

l

不经过点

P

且与椭圆

C

相交于

A

，

B

两点．若直线

PA

与直线

PB

的斜率之和为1，问直线

l

是否过定点？证明你的结论．易得椭圆方程为可设直线

l

的方程

y

=

kx

+

m

，

A

(

x

，

y

)，

B

(

x

，

y

)，运用方程思想将直线方程与椭圆方程联立，通过韦达定理得

x

+

x

再由直线

PA

与直线

PB

的斜率之和为1得整理得化简得2

m

-3

m

+8

k

+12

k

-10

km

=0，因式分解得(

m

-4

k

)(2

m

-2

k

-3)=0，从而确定直线

l

：

y

=

k

(

x

+4)过定点(-4，0)．在高三一轮复习过程中，笔者发现，学生能熟练运用方程思想联立方程组，并通过韦达定理得

A

，

B

两点坐标之间的关系，解题的难点在于，转化条件

k

+

k

=1后得到的关于

k

，

m

的二次式该如何处置？有经验的学生知道要因式分解，但不知如何分解

.

如果能顺利分解因式，问题就迎刃而解．教学中教师如果仅仅告知学生，这一步需要因式分解，即便教会学生“双十字相乘”因式分解法，学生对于相似的题型仍然是茫然的．解题教学不应当局限于这一道题的解法，更应引导学生厘清问题的本质．笔者认为，有几个问题是必须要搞清楚的： ①为什么直线

l

过定点？②为什么需要因式分解？③因式分解后得到的因式之一恰好过点

P

，这是偶然还是必然？④最后求得的定点在

x

轴上，这又是偶然还是必然？首先关于问题①②，直线

l

的方程为

y

=

kx

+

m

，由于

k

+

k

=1，直线

l

中的参数

k

，

m

必然有着确定的关系，故直线

l

有可能过定点或定斜率；反之，若直线

l

过定点，则必存在

k

与

m

的线性关系，故得到关于

k

，

m

的二次式后需要想办法进行因式分解．其次，要解决问题③④，就需要搞清楚直线

l

是如何变化的

.

教学中可用几何画板或GGB等作图软件来动态演示直线

l

的变化规律

.

由于

k

+

k

=1，那么

k

确定，

k

随之确定，故只需通过运动点

A

来探究变化规律．当点

A

沿椭圆无限趋近于点

P

时，

k

就无限接近椭圆在点

P

处的切线的斜率，由椭圆上任一点(

x

，

y

)处的切线斜率为可知，

k

无限接近而此时，由于

k

+

k

=1，点

B

也在沿椭圆无限趋近于点

P

，故

k

也无限接近直线

l

在无限逼近点

P

处的切线

l

．另一方面，当直线

PA

的斜率无限增大，趋向于 +∞时，直线

PB

的斜率无限减小，趋向于-∞，此时，直线

l

无限逼近点处的切线

l

．

l

与

l

斜率显然不等，故直线

l

不可能定斜率，可能过定点，

l

与

l

关于

x

轴对称，则所经过的定点必在

x

轴上，即为

l

与

l

的交点(-4，0)．

3 极限思想的运用

3

.

1 寻找极限位置，确定定点

事实上，对于引例，我们可以作更深层次的思考，若改变题设条件，将“

k

+

k

=1”改为“

k

+

k

=2”，其余条件、问题不变，探究直线

l

的变化规律．不妨考虑某些特殊位置，当

k

=

k

=1时，直线

l

的极限位置是椭圆在点处的切线

l

；当直线

PA

的斜率无限增大，趋近于 +∞时，直线

PB

的斜率无限减小，趋近于-∞时，直线

l

的极限位置就是椭圆在处的切线

l

，显然，

l

与

l

斜率不等，故直线

l

过定点即为

l

与

l

的交点．更一般地，已知

P

(

x

，

y

)为曲线上一点，设直线

l

不经过点

P

且与椭圆

C

相交于

A

，

B

两点．若直线

PA

与直线

PB

的斜率之和为

λ

，则直线

l

过定点而且，由于证明过程是可逆的，反之也成立．顺势而为，教学时还可以引导学生探究：若

k

k

=1，直线

l

是否过定点？推广到一般，已知

P

(

x

，

y

)为曲线上一点，设直线

l

不经过点

P

且与椭圆

C

相交于

A

，

B

两点．若直线

PA

与直线

PB

的斜率之积为则直线

l

过定点探究动直线的变化规律，寻找极限位置，能快速确定定点位置．

3

.

2 利用极限位置，计算定值

例1

已知椭圆的离心率为椭圆

C

的下顶点和上顶点分别为

B

，

B

，且

B

B

=2,过点

P

(0，2)且斜率为

k

的直线

l

与椭圆

C

交于

M

，

N

两点．求证：直线

B

M

与直线

B

N

的交点

T

的纵坐标为定值．

解析

易得椭圆的标准方程为+

y

=1，设

M

(

x

,

y

)，

N

(

x

,

y

)，设直线

l

的方程并和椭圆进行联立，得设

T

(

m

，

n

)，再由

B

，

T

，

M

在同一条直线上，得在同一条直线上，得化简得故交点

T

的纵坐标为定值点评 换个角度来思考该问题，直线

l

在变化过程中，极限位置是与椭圆相切，此时直线

B

M

与直线

B

N

交于一点，该点即为直线

l

与椭圆相切的切点，该点的纵坐标即为所求．利用极限思想，可以快速确定定值．

3

.

3 运用极限思想，求解范围

例2

设双曲线的左、右焦点分别为

F

，

F

．若点

P

在双曲线上，且△

F

PF

为锐角三角形，则

PF

+

PF

的取值范围是

．

解析

由已知得则设

P

(

x

，

y

)是双曲线上任一点，由对称性不妨设

P

在双曲线的右支上，则1<

x

<2，

PF

=2

x

+1，

PF

=2

x

-1，∠

F

PF

为锐角，则即(2

x

+1)+(2

x

-1)>42，解得所以则点评 利用极限思想，不妨考虑极限位置(由于双曲线的对称性，可将点

P

置于第一象限来考虑)，当△

F

PF

为直角三角形时，有两种情况：若∠

F

PF

为直角，

PF

+

PF

=2；若∠

PF

F

为直角，

PF

+

PF

=8

.

由图形上点

P

的运动规律可知，△

F

PF

为锐角三角形时，对于填空题，利用极限思想解决范围问题，省时省力；对于解答题，先探究动点的运动轨迹，可以帮助确定变量

.

如该题中，

PF

+

PF

的变化源于点

P

，点

P

在第一象限的变化可由横坐标这一单一变量控制，于是只需用点

P

的横坐标来表示目标．引导学生利用极限思想来求解范围，从运动的观点来解决问题，有利于发展学生的理性思维．

4 几点教学建议

4

.

1 分析极限状态，明辨解题思路

例3

已知直线

y

=2

x

与椭圆

E

：

x

+2

y

=1交于

A

，

B

两点(点

A

在第一象限)，点

P

(-4

t

，

t

)在椭圆

E

内部，射线

AP

，

BP

与椭圆

E

的另一交点分别为

C

，

D

．求证：直线

CD

的斜率为定值．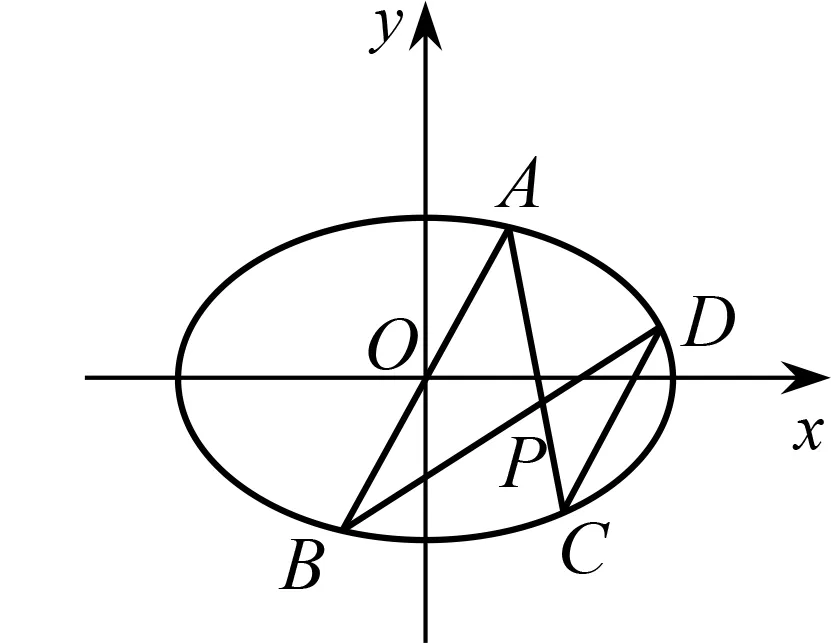

图2

解析

对于该题，易想到的思路是求出

A

，

B

两点，联立直线

AP

与椭圆方程得

C

点坐标，联立直线

BP

与椭圆方程得

D

点坐标，再求直线

CD

的斜率．但是，该思路计算量很大，求解困难．不妨利用极限思想重新审视该题，点

P

在定直线上运动，显然直线与椭圆有两个交点，当点

P

无限接近这其中一个交点时，直线

CD

的极限位置就是在该交点处的切线，那么直线

CD

的斜率即为该切线的斜率，易得斜率为2．还可以考虑另一个极限位置，当点

P

无限接近坐标原点时，直线

CD

的极限位置就是直线

AB

，故直线

CD

的斜率为2．预知直线

CD

的斜率为2，那么该题的证明思路就更加清晰了，即需证明

AB

∥

CD

，联想到向量，即证

λ

=

λ

．解析几何的解题思路非常重要，因为计算量大，往往“没有回头路”，教学中一定要引导学生先分析解题思路，理清楚解题步骤，预估计算量，计算时多想两步，才能简化计算，高效解题．利用极限思想判断出直线

CD

的斜率为2，为后续的证明打开了思路，抓住了变化中的不变量，解题方向更加清晰．

证明

设

P

(

x

，

y

)，

A

(

x

，

y

)，

B

(

x

，

y

)，

C

(

x

，

y

)，

D

(

x

，

y

)，则又设其中

λ

，

λ

∈

R

，则代入椭圆

x

+2

y

=1并整理得从而有①

同理可得，②

结合

x

=-4

t

，

y

=

t

，

A

，

B

两点均在直线

y

=2

x

上

.

由①-②，得因为所以

λ

=

λ

．从而

AB

∥

CD

，故

CD

的斜率为定值．

4

.

2 妙用极限思想，优化解题过程

例4

已知抛物线

C

：

y

=8

x

，在

x

轴的正半轴上，是否存在某个确定的点

M

，过该点的动直线

l

与抛物线

C

交于

A

，

B

两点，使得为定值？如果存在，求出点

M

的坐标；如果不存在，请说明理由．

解析

假设存在满足条件的点

M

(

m

，0)(

m

>0)，设直线

l

：

x

=

ty

+

m

，与抛物线方程联立，有设

A

(

x

，

y

)，

B

(

x

，

y

)，有

y

+

y

=8

t

，

y

y

=-8

m.

当

m

=4时，为定值，所以

M

(4，0)．点评 假设存在点

M

满足条件，因为过点

M

的任意一条弦为定值，那么对于垂直于

x

轴的弦

AB

也满足．当直线

AB

垂直于

x

轴时，设

M

(

x

，0)，

A

(

x

，

y

)，

B

(

x

，-

y

)，则对于这一特殊位置，还不能确定定点和定值，不妨考虑另一个极限位置．当点

A

无限接近原点

O

时，点

B

沿

x

轴无限延伸，横坐标趋向于趋向于趋向于令可得

x

=4，故预判出定点为(4,0)，那么后续只需证明点过的任一弦

AB

均有提前预判出定点和定值，那么解题过程中就不需要设2个参量，只需引入直线的斜率这一个参量即可，这就大大简化了计算，优化了解题过程，这对于计算能力薄弱的学生是非常必要的．

在上述例题中，动直线的极限状态往往是切线或过已知点状态，若动直线过定点，则极限状态也过定点，所以两种极限状态下同时满足的定点通常可以预判，这样也给我们后面的解答指引了目标，即便用常规方式计算也会因此由漫无目的变得有的放矢．例如双二次的因式分解因为定点已知，从而分解更加容易．

4

.

3 活用极限思想，提升核心素养

面对新高考，我们总在强调“思维能力的培养”，这不仅是一句口号，而是需要一线教师在教学过程中不断摸索的

.

过去，我们在课堂中常会帮助学生总结解决问题的一般方法并归纳分类，这对于应试是能起到一定作用的，但题目是千变万化的，如何能让学生在面对各种问题时，自我分析，自我探究，自我解决，是需要教师不断引导的

.

虽说极限思想不能直接用来求解圆锥曲线综合题，但是对于引导学生学会自我探究起到了积极的作用

.

上述例题中，利用极限思想来解决的过程，均是抓住了题目中的动点和动直线，寻找变化规律，这对于学生来说，是提升理性思维、抽象能力的绝佳时机

.

解题教学时，唯有多想一点，才能少算一点，多反思才能不断优化解题过程，多总结归纳才能以不变应万变，多复盘才能不断提升．数学教育的本质是传授数学思想，教学生学会思考

.

极限思想在高中数学中的运用，不仅能提升学生的解题能力，还能提升核心素养，让学生站在更高的角度去思考、理解问题，知其然并知其所以然，更为今后高等数学的学习奠定基础．