以小见大 聚焦变化 指向素养——以一道“函数探究题”的改编为例*

周 炼

(江苏省泰州市第二中学附属初中 225399)

2022年4月7日，江苏省泰州市教育局教学研究室举办了全市初中数学教师命题比赛

.

此次比赛以提升初三数学教师命题能力、推进初中数学命题改革、更好落实双减政策以及新高考下教学模式的转变为主要目的，同时也激发了全市初中数学教师以及教研员的命题热情

.

比赛分两种模式：改编试题与原创试题

.

笔者选择了改编试题中的一道函数题作为初始素材，借助于几何画板等工具，从结构优化、问题设计、思想升华等方面对试题展开了深入研究，并在改编过程中形成了一些主张与想法，下文作具体阐述

.

1 试题原型与改编

1

.

1 试题原型

在平面直角坐标系

xOy

中，抛物线

y

=

x

-4

x

+3与

x

轴相交于点

A

，

B

(点

A

在点

B

的左侧)，与

y

轴相交于点

C.

(1)求直线

BC

的表达式

.

(2)垂直于

y

轴的直线

l

与抛物线相交于点

P

(

x

，

y

)，

Q

(

x

，

y

)，与直线

BC

交于点

N

(

x

，

y

)

.

若

x

<

x

<

x

，结合函数图象，求

x

+

x

+

x

的取值范围

.

1

.

2 改编呈现

在平面直角坐标系中

xOy

中，抛物线

y

=

a

(

x

-

m

)(

x

-

n

)(

a

<0，

m

<

n

)与

x

轴交于点

A

，

B

(点

A

在点

B

的左侧)，与

y

轴相交于点

C.

直线

y

=

c

与抛物线相交于

P

(

x

，

y

)，

Q

(

x

，

y

)两点(

P

与

Q

不重合)，与直线

BC

交于点

N

(

x

，

y

)

.

(1)设

a

=-1，

m

=1，

n

=3

.

①求线段

AB

的长；②证明：当

c

<1时，一定存在不重合的

P

，

Q

两点且

x

+

x

的值不会随着

c

的变化而变化

.

(2)令

c

=

m

，且点

A

在直线

BC

的上方

.

①求

m

的取值范围；②一定存在一个

a

的值，对于任何符合的

m

,

n

均可以使得

x

+

x

-

x

为常数，求

a

的值以及

h

的取值范围

.

2 改编策略

2

.

1 以小见大的维度延伸

·将参数一般化，以拓宽试题的内容

一道试题的背后，往往是命题者对试题所涉及的方方面面进行透彻研究的结果，但考虑到学生的思维水平与接受程度，一般都会对结论作特殊化处理，以更加具体的问题情境作为呈现载体

.

但在改编一道试题时，若依旧停留在特殊化阶段，命题的视野与格局便无法打开，看到的也仅仅是特定条件下的固化结论，不具备迁移性与推广性，更谈不上创新与发散

.

若想要激荡出更多的灵感就要先将试题一般化，对于函数题来说主要是将参数一般化，这是一个由点到面再由面到点的过程，只有经历了这样的过程，才会形成更丰富、宽广、多元化的良好命题样态

.

本题函数原型是一个完全确定的二次函数，但若囿于某个具体的函数表达式，改编的范围便会十分狭隘，延伸面也较小

.

为了创造出更多的可能性，势必要将抛物线

y

=

x

-4

x

+3推广为更一般的形式

.

经分析，发现该函数在整个问题中与

x

轴的两个交点密切相关，所以将其一般化为交点式

y

=

a

(

x

-

m

)(

x

-

n

)是比较合理的，这样便能在紧扣原型的基础上以小见大地切入

.

至于原型中的直线，在改编时一开始给出的是一般形式

y

=

c

，但由于后续要研究更具体的存在性问题，在多次尝试后发现令

y

=

m

能与

y

=

a

(

x

-

m

)(

x

-

n

)产生更为具体的、个性化的代数关联，最终确定“

a

，

m

，

n

”为本题的参数设定

.

·将结构层次化以促进思维的递进

试题改编不同于直接命题，因为试题原型本身是有研究基础的、是原命题者思维的结晶，所以相当于站在“巨人的肩膀”上再研究、再发现

.

试题改编虽要立足并尊重原型，但更要高于并突破原型，要能在已有研究成果之上彰显创造性

.

而正是这样逐渐往高处走的趋势，反而有可能会在改编后变得“不接地气”，甚至与学生的思维水平出现断层

.

为了避免这样的状况发生，当改编后的问题比较抽象或思维过于密集时，可以为其设置有层次的递进结构，通过从特殊到一般的引导，给学生创造一个小的切口，再从这个切口出发以小见大、循序渐进地展开研究

.

本题改编共有三处在结构层次化以促进思维递进方面作了较为周密的思考

.

例如在(1)①中设计“计算线段

AB

的长”这一问题，是因为在(2)①中要求

m

的范围需要先算点

A

，

B

，

C

的坐标，而后者在引入参数后对运算的要求更高，有了①的铺垫，学生对于

A

(

m

，0)，

B

(

n

，0)，

C

(0，

amn

)，

y

=-

amx

+

amn

这样含参数的坐标与函数表达式的接受度会更高，在运算时也就有迹可循

.

同样地，还有(1)②中设计“证明当

c

<1时，一定存在不重合的

P

，

Q

两点”这一问题，是希望学生能关注到直线与二次函数图象不是一直存在交点的，会受到一些参数范围的限制，而这样的认识对于(2)②中“一定存在一个

a

的值，对于任何符合的

m

，

n

”这一条件的理解会更加深刻，从而联想到这一范围可能与

x

，

x

的存在性相关

.

最后，在(1)②中设计“证明

x

+

x

的值不会随着

c

的变化而变化”这一问题，依旧是为(2)②中探究“

x

+

x

-

x

”是否为定值埋下了伏笔，引导学生将简单情境中得出的

x

+

x

的性质自主迁移到最后一问中去

.

像这样逐层递进、从特殊到一般的良好试题结构可以引导学生进行类比，以此激发出更多的联想，能沿着一条清晰的思维链条逐渐向上攀登

.

2

.

2 聚焦变化的改编理念

变化是一切事物的本质特征，或者说这个世界上唯一不变的就是变化

.

在问题改编的过程中赋予变化视角，往往能看到事物的多面性

.

但杂乱无章的变化是没有研究价值的，一般来说，不变性与存在性是在变化情境中研究问题的两个常见维度，以此重新审视问题往往会获取不一样的探究视角

.

本题改编原型的第二问就蕴涵着丰富的变化因素，例如在动直线平移的过程中找到符合

x

<

x

<

x

的图象位置，这是一种变化中的存在性；发现

x

+

x

+

x

中的

x

+

x

不会随着直线位置的变化而变化，这又体现出了一种变化中的不变性

.

作为改编，虽然不能完全照搬原问题的设计，但其背后的思想、方法是可以延续甚至升华的

.

聚焦变化既是对原型的一种继承与发扬，同时也是以多样化视角寻求改编新意的重要契机

.

·变化中的不变性

原型中关于变化中的不变性是相对隐蔽的，再加上题目中并没有直接给出研究不变性所需的参数，对于代数意识较弱的学生可能会出现入门障碍

.

另一方面，设出参数后的推理过程相对简单，也不能充分体现学生的代数素养

.

基于此，决定在原型基础上在两处分别降低、提升一个维度对变化中的不变性进行改编

.

第一处：在(1)②中通过引入变量

c

，构建了无论

c

取何值，都不影响

x

+

x

恒为定值的结构设计

.

对比原型来看，将“垂直于

y

轴的直线

l

”具体化为函数表达式

y

=

c

，这实质上是多铺设了一层台阶，帮助学生搭建了设参数描述函数交点的脚手架，避免了在原型中由于缺乏参数意识造成一部分学生在一开始就陷入无从下手的“恐慌”局面

.

学生在得到抛物线表达式

y

=-

x

+4

x

-3后，只要令-

x

+4

x

-3=

c

，再根据

c

<1便可得

Δ

=4(1-

c

)>0，从而发现一定存在不重合的

P

与

Q

两点

.

第二处：在(2)②中将原型中垂直于

y

轴的直线

l

设定为

y

=

m

后，发现当

a

取任意值时，与之间没有必然的数量关系(如图1、图2)，但是将

a

取为-1后，无论怎样改变

m

与

n

的值，一直存在着不变的数量关系(如图3、图4)

.

利用这样的关系构造为

M

·

x

模型便可以将其设计为任意中的确定问题，其中

M

代表了题目中的所有变量，而

x

则是关于要确定位置的常量的代数式，一般来说将变量提取后，令后面含常量的代数式的值为0，即可让变量消失，从而让变量的变化不影响整体的取值，以达到变化中不变的效果

.

具体地，令

y

=

m

可得

ax

-

a

(

m

+

n

)

x

+

amn

-

m

=0，解得

x

+

x

=

m

+

n.

再令-

amx

+

amn

=

m

，又可以解得从而因为存在一个

a

的值使得

x

+

x

-

x

为常数，所以在中令即

a

=-1，此时

x

+

x

-

x

与

m

无关，为常数0

.

这与原型中的问题有所区别的是，它需要满足某个特定的前提条件，要找到某个特殊位置才能让某个量不会随着变量的变化而变化，这在原型思维层级的基础上又多了一层探究性与不确定性，对学生的能力要求自然也就更高

.

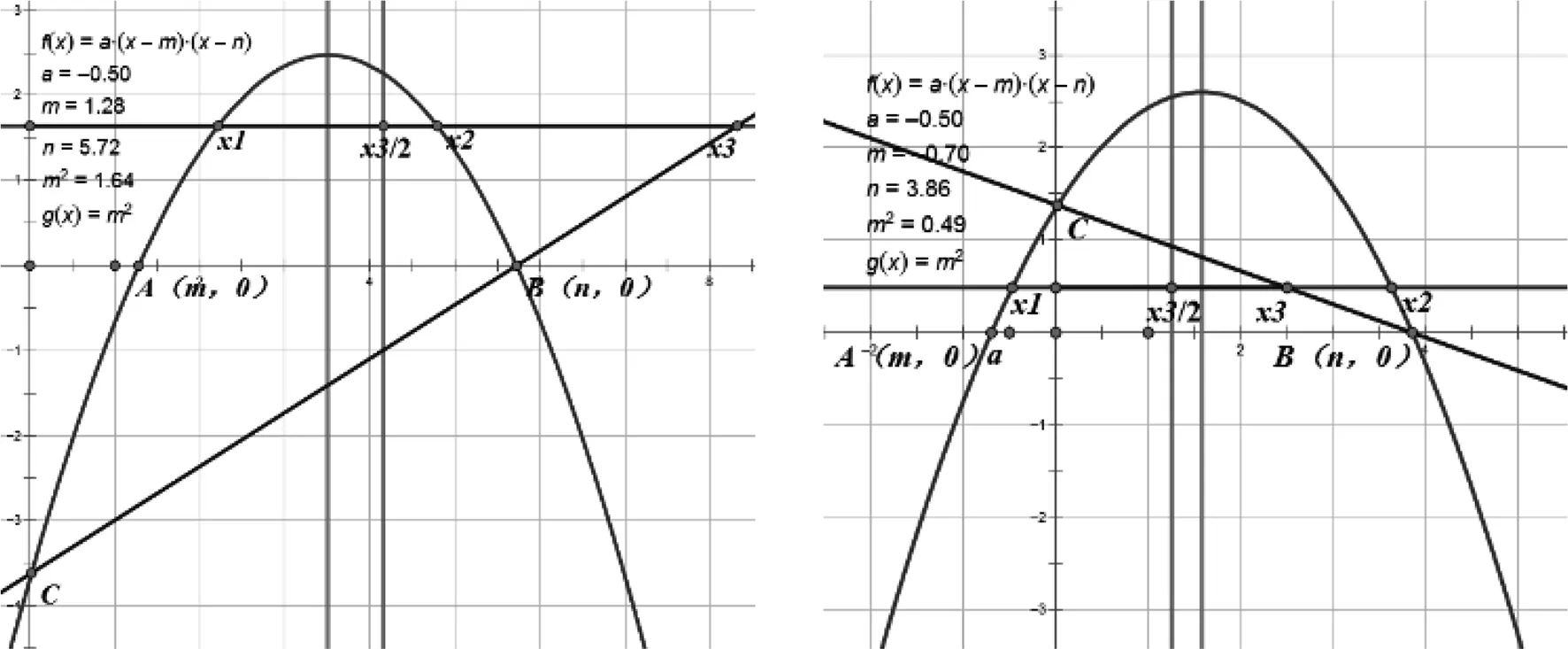
图1 图2

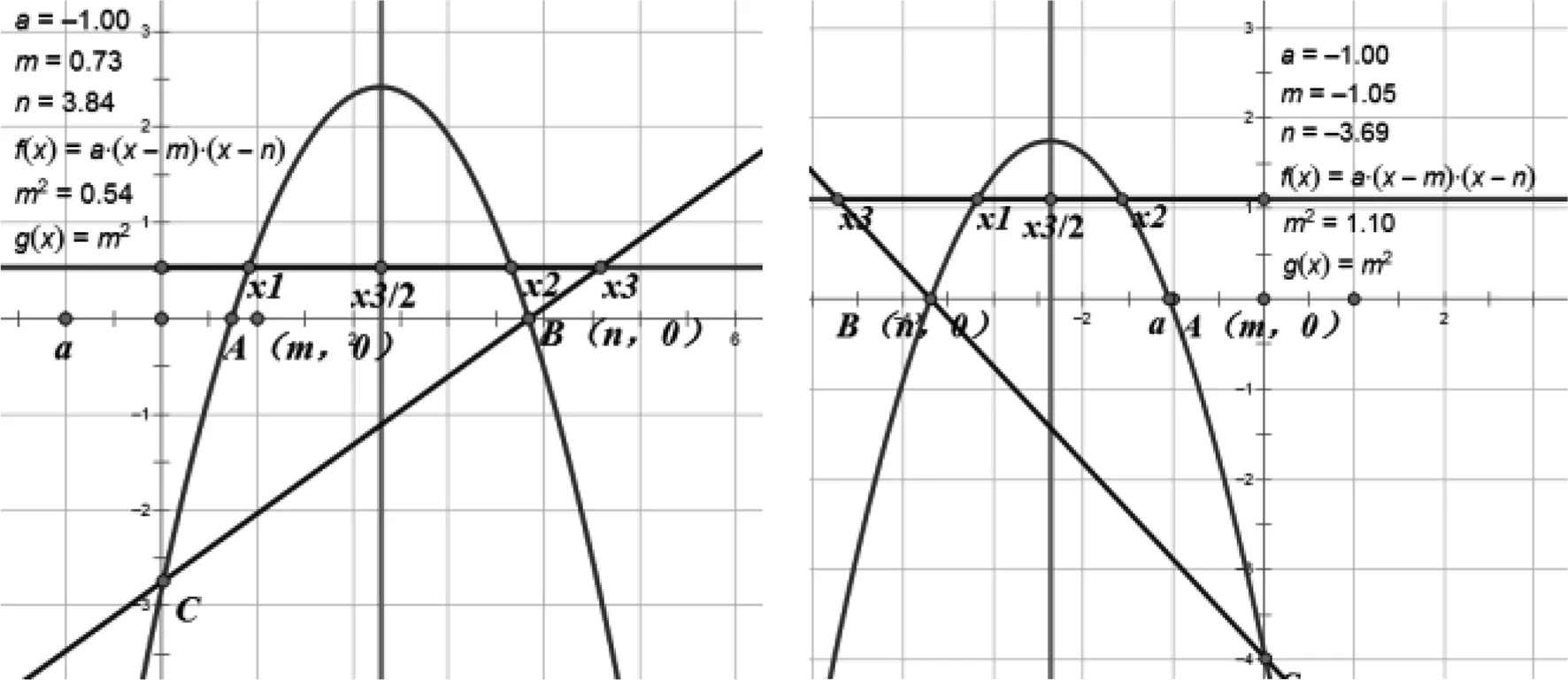
图3 图4

·变化中的存在性

由于重新设定的问题背景融入了大量参数，所以函数图象相较于原型结构固化的缺陷，有了更加自由的延伸与探索空间

.

在改编时可以对不同的参数赋值，通过观察、分析、推算、验证等方法以发现更多变化中的存在性，并将其设定为范围求值、证明等问题，从而将试题改编再推上一个新的高度

.

本题共有两处改编体现了变化中的存在性

.

图5

第一处：在(2)①中“已知点

A

在直线

BC

的上方，求

m

的取值范围”正是基于原型中“求直线

BC

的表达式”、指向存在性研究的改编

.

在改编时，借助于几何画板对不同的参数赋值使图象位置发生变化，发现在变化的过程中点

A

时而落在直线

BC

的下方(如图5、图6)，时而落在直线

BC

的上方(如图7)，并且无论怎样改变

n

值的大小，都不影响点

A

与直线

BC

的位置关系，唯独当

m

分别为正值与负值时，才会产生两种不同的位置状态

.

本题以点

A

在直线

BC

的下方作为要满足的存在性要求对原型进行了改编，发现通过代数推理可得0>-

am

+

amn

，因为

a

<0，所以

m

<

mn.

解这个不等式需要分类讨论：如果

m

<0，那么

m

>

n

，但这与条件中的

m

<

n

矛盾，不符合题意需要舍去；如果

m

>0，那么

m

<

n

，符合题意

.

图6 图7

第二处：在(2)②中“

x

+

x

-

x

为常数”讨论的前提是“对于任何符合的

m

与

n

”均成立的任意性，而原型中关于“

x

<

x

<

x

”并未提出相关参数使问题恒成立的范围要求，但

x

与

x

一定存在吗？在对原型进行改编时尤其侧重了对这一现象的研究

.

在用几何画板绘图时发现

x

必然存在，但当直线位于抛物线顶点上方时是不存在

x

与

x

的(如图8、图9)

.

此时设定条件“一定存在一个

a

的值”是为了控制直线

y

=

m

与抛物线图象必须存在交点

.

从代数角度看，也就是联列两个函数表达式后根的判别式要大于0，即在

x

-(

m

+

n

)

x

+

mn

+

m

=0中，

Δ

=(

n

-3

m

)(

m

+

n

)>0

.

对于该不等式的讨论一般要分同正或同负两种情况，略微繁琐，但若直接给出其中一项的正负性又会让题目缺乏层次感，过于浅显

.

在秉持着简约命题理念的同时又希望能蕴含较为丰富的推理内容与素养成分，最终决定给出条件其中

h

为可以任意赋值的常数；只要选择合适的

h

的范围，就可以使交点一直存在

.

具体地，因为所以

n

与

m

同号，由①可知

m

>0，那么

n

>0，

m

+

n

>0，所以

n

-3

m

>0，即要在时结论一定成立，便有

h

≥3

.

正是

h

这样一个新参数的引入让本题焕发出了新的生命力，在常数与变量、恒成立与存在性的差异与统一中使得问题的代数意蕴更加浓厚，指向了更高阶的代数素养

.

图8 图9

3 素养表现

3

.

1 扎实的运算功底

参数引入是本次改编的一大特点，除了第一问的题①是解简单的一元二次方程，后面三个问题均涉及一定量的参数，而在参数较多的情况下能根据法则和运算律进行正确运算，是代数素养达成的一种高度体现

.

相较于小学阶段更加注重式的研究，初中阶段更关注学生的抽象思维能力，在脚手架搭建合理的情况下适当设置一些参数，可以反映出学生能否选择合理的运算策略以解决结构不良的代数问题，并以此促进学生运算素养的发展，这也有助于形成规范化思考问题的品质，养成一丝不苟、严谨求实的科学态度

.

3

.

2 必要的几何直观

改编后的问题只有第一问给出的是具体函数，但随着解题的不断推进，学生会愈发感受到函数的抽象性，越来越觉得无从下手，事实上这是参数增多后所引发的必然结果

.

本题之所以没有画出函数图象，就是希望学生能尝试着自己主动画图，通过图象让抽象的代数研究更加具体，以发展运用图表描述和分析问题的意识与习惯，逐渐形成几何直观的数学素养

.

前面提到，改编时问题的结构设置是逐层递进的，学生可以先从第一问中的具体函数图象开始画起，并以此类比画出后面抽象函数的大致草图建立形与数之间的联系

.

当然，仅仅依靠图象分析并不能完全说明问题，依旧需要借助于计算与推理进行说理

.

但构建直观模型对于把握问题本质、明晰研究路径等方面的优势是不言而喻的，它能让思维看得见、摸得着，让推理有迹可循

.

3

.

3 严密的推理能力

推理能力主要是指从一些事实和命题出发，依据规则推出其他命题或结论的能力

.

本题虽然是一道代数题，但对学生的推理能力却有相当的要求，尤其是最后一问，当学生面临很多参数与不等式时，要将这些不等关系加以综合、分析以形成一条清晰的推理主线，是需要非常严密的整合能力的

.

另外，以小见大、聚焦变化的改编方式，也让题目中整体结构从特殊到一般的类比，关于存在性与不变性的分析、表述都建立在了逻辑性的基础之上

.

由此看来，改编后的试题需要学生较强的推理能力

.

相信经历了这样的过程后，可以让学生感悟到数学的严谨性，有助于培养学生重论据、合乎逻辑的思维方式，形成实事求是的科学态度与理性精神

.