锁脚锚杆对软岩隧道支护的有限元数值模拟

侯代英,李振雨,李政兴,马东东

（中交一公局集团有限公司,北京 100024）

0 引言

在实际工程中，软岩隧道支护是隧道支护的一个难题，这是由于软岩自身所具有的遇水易软化、变形大且强度低等的缺点。由于软岩的这些缺点，给设计和施工带来了一定的困难，而且会在一定程度上影响隧道的长期稳定性。

为了解决软岩问题，我国学者做了大量的研究[1-4]，这些研究对实际工程问题的解决提供了有力支持。近年来，中国学者以实际工程为背景对软岩隧道的具体问题进行了分析[5-7]，蒙浩[8]以某地特长软岩公路隧道的结构设计为例，分析和阐述了隧道主导思路设计与工程施工的技术手段，为类似的工程施工建设具有一定的指导作用和参考价值。宋洋等[9]建立了一个基于软岩的流变特性的隧道模型，在地震荷载的作用下并利用三维有限差分软件FLAC3D软件，分析了不同支护刚度条件下围岩变形和支护体应力情况。

该文以临渭高速公路某隧道为研究对象，对软岩区域工程地质资料和支护参数开展监测分析，在现有的隧道工程建设和文献资料的基础上调查、检索、学习，并应用数值模拟和现场测试手段，对软弱围岩段支护体系进行静力状态分析，对不同工况的隧道支护结构的稳定性和安全性进行评价并提出合理的支护措施。

1 有限元模拟

1.1 工程背景

该研究依托工程某软岩隧道，该隧道的建筑限界净空净宽为13.428 2 m、净高7.11 m。隧道采用单心圆（净面积A=79.02 m2），选用锚索和锚杆两种支护方法进行支护，以钢筋网、湿喷混凝土等结合锚索或者锚杆作为初期支护，形成内复合式衬砌结构；并以钢拱架、超前大管棚、钢格栅、注浆和超前锚杆等措施作为辅导设施，使围岩能够发挥自身的承载能力；接下来进行初期支护和二次模筑衬砌的施工，以便指导施工，应在施工过程中全程监控量测。通过理论计算分析并结合类似工程的经验，确定初期支护参数，隧道洞身段的进洞口采用超前管棚结构。为了更好地指导隧道施工，监测监控支护结构选择在隧道的左线，所在位置的围岩级别为Ⅴ级。

1.2 边界条件

位移边界条件为：左、右边界的水平方向位移为0，即U2=0，下边界的位移边界条件为固定边界U1=U2=0，上边界为自由边界。

应力边界条件为：由于工程的复杂性和多变性，在数值模拟过程中采用以下假定：隧道周围的土体和岩体为均质体，忽略场地内构造活动的影响。通过计算取垂直应力，水平应力为侧压系数与垂直应力乘积，即其中K0为土的侧压系数。

1.3 建立模型

模型所采用的有限元软件为Midas/GTS，取隧道埋深为：80.298 3 m的位置，在模拟区域的选择上，向左、右、下方向各取30 m，上部按工程勘察资料选取80.298 3 m。土层及其参数如表1所示，模拟过程中，岩体的本构模型采用摩尔库仑模型。在模拟复合衬砌的开挖过程中，考虑建立动态施工过程，建模过程中，使用杆单元模拟锚杆，使用壳体结构单元模拟衬砌，衬砌厚度为30 cm。二次衬砌需要控制其变形，采用弹性模型进行模拟，混凝土喷涂层厚度为45 cm。考虑隧道的结构形式，想要得到可靠的计算结果，在内部划分细密，隧道内及周围采用细密网格划分，然后向外延伸，在外围做划分网格的辅助圆，相应的网格单元如图1所示。

根据设计资料，提取出相关的材料参数如表1所示。

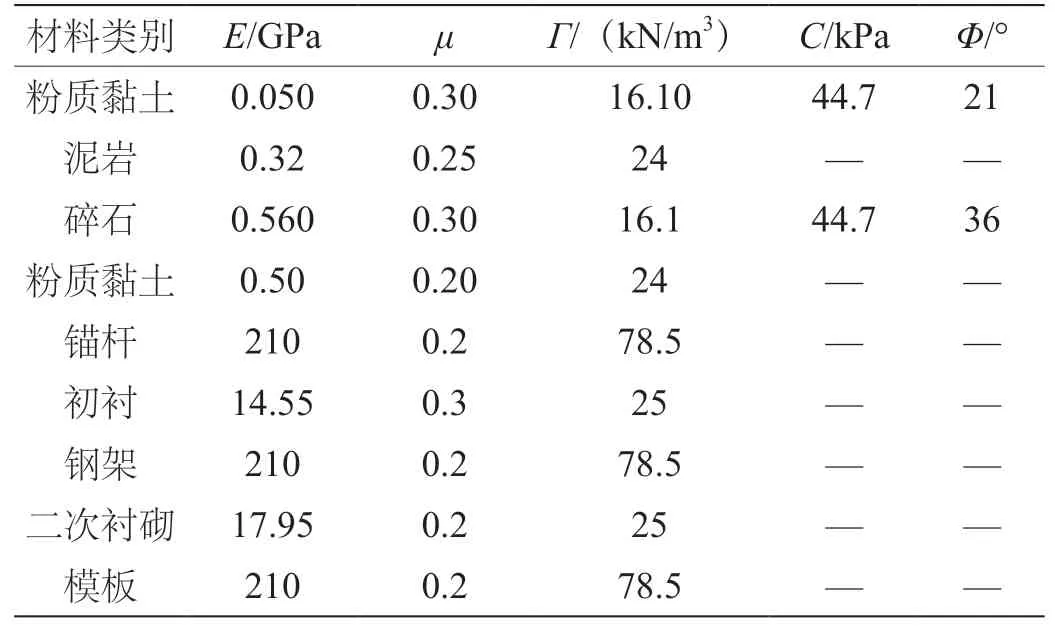
表1 计算模型参数

1.4 开挖施工阶段模拟

施工过程所选用两种支护方法，即系统锚杆支护和锁脚锚杆支护，实际施工过程中，系统锚杆每个阶段的施工步序包括开挖和施工衬砌，主要为：初始阶段→上部开挖阶段和上部初衬→中部开挖和中部衬砌→下部开挖和下部初衬→二次衬砌和下部回填。

锁脚锚杆支护的施工步序为：初始阶段→上部开挖阶段和上部初衬→中部开挖和中部衬砌→下部开挖和下部初衬→二次衬砌和下部回填。

2 数值模拟结果比分析

2.1 总位移的施工阶段数值模拟

2.1.1 加系统锚杆的施工阶段模拟

将该次模拟的系统锚杆稳定的位移结果情况作对比，如图2所示。

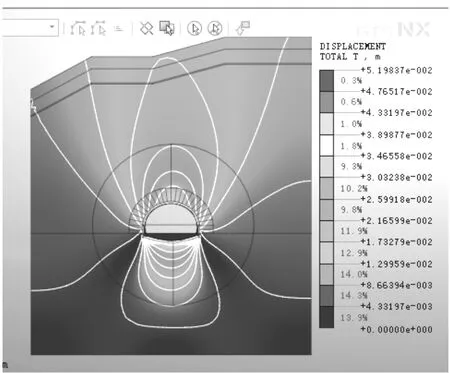
图2 系统锚杆总位移的数值模拟

从图2可以看出其最大位移发生的位置在拱顶和仰拱的位置。这样对于拱顶和仰拱位置的支护要求比较高。

2.1.2 加锁脚锚杆的施工阶段模拟

将该次模拟的锁脚锚杆稳定的位移结果情况作对比，如图3所示。

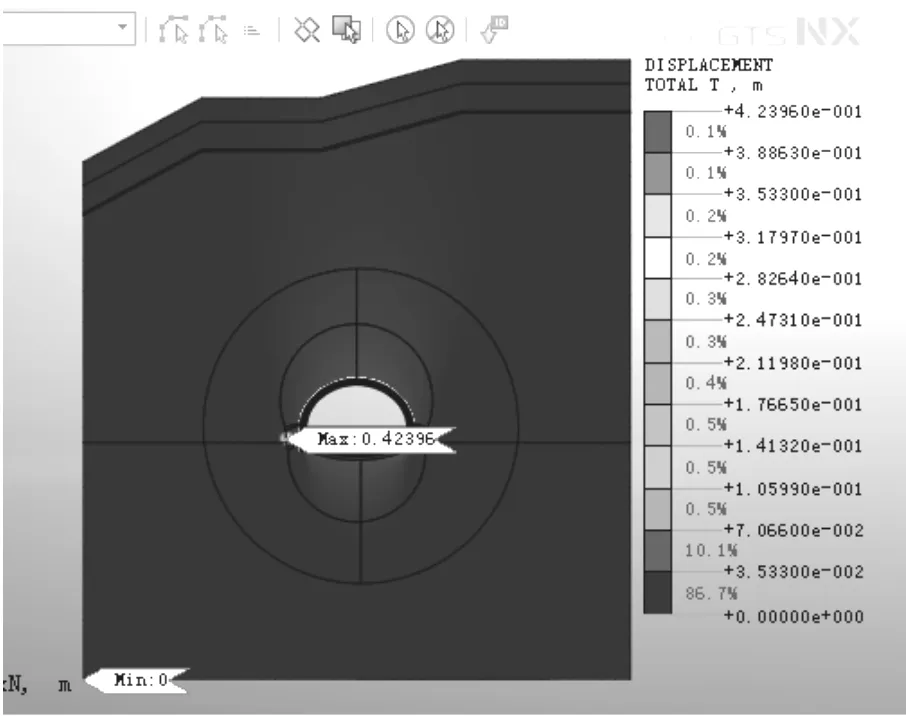
图3 锁脚锚杆总位移的数值模拟

从图3可以看出，总位移变化最大的位置在锁脚锚杆的另一端，即在加锁脚锚杆后，软岩通过钢架把力传递给锁脚锚杆，由于钢架的刚度大，导致拱顶的位移相对锁脚锚杆端部的位移较小。

通过有限元模拟对拱顶的位移标记记录其在各个施工阶段的位移变化规律，对比系统锚杆与锁脚锚杆支护下软岩隧道的拱顶总位移随开挖阶段的变化曲线，其变化如图4所示。

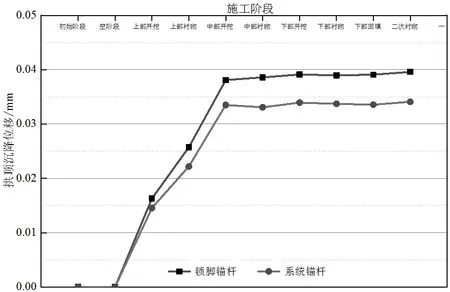
图4 锁脚锚杆和系统锚杆的各施工阶段总位移变化规律

从图4可以看出系统锚杆支护和锁脚锚杆支护的总位移的变化规律，各阶段锚索支护的位移相对于锚杆支护较大，但都满足设计要求。从前面这些图可以看出，锚杆支护的软岩隧道最大拱顶位移0.034 1 mm，锁脚锚杆支护软岩隧道最大拱顶位移为0.039 51 m，两者都满足最小变形的要求，但相对于其各自的支护方式，系统锚杆的材料用量远远比锁脚锚杆多，使用锚索比较经济，很大程度上节约了材料。

2.2 垂直位移的施工阶段数值模拟

2.2.1 加系统锚杆的总位移

将该次模拟结果中围岩稳定后的垂直位移情况作对比，如图5所示。

观察图5可以发现，在系统锚杆的支护下，软岩隧道的最大位移位置出现在拱顶，上拱顶的沉降最大，下仰拱出现的最大上凸位移。

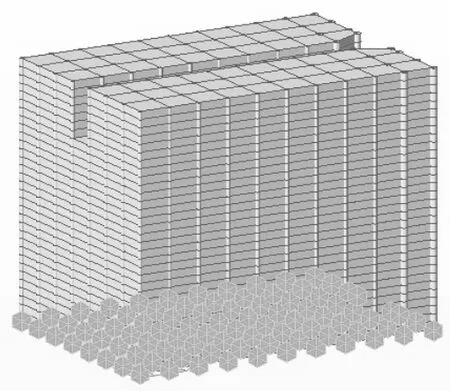
图5 千斤顶反力座模型

2.2.2 加锁脚锚杆的垂直位移

将该次模拟结果岩稳定后的垂直位移情况作对比，如图6所示。

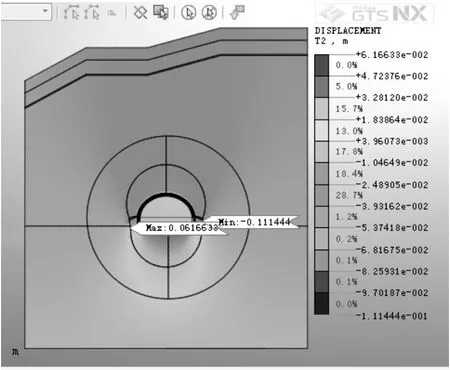
图6 锁脚锚杆垂直位移的数值模拟

从图6可以看出在锁脚锚杆支护方式下隧道开挖隧道的垂直位移的特点，最大位移发生的位置不在拱顶，而在锁脚锚杆支护的另一端。

通过有限元Midas GTS NX进行模拟，并记录了软岩隧道拱顶的竖向位移在不同施工阶段的变化规律，其变化规律如图7所示。

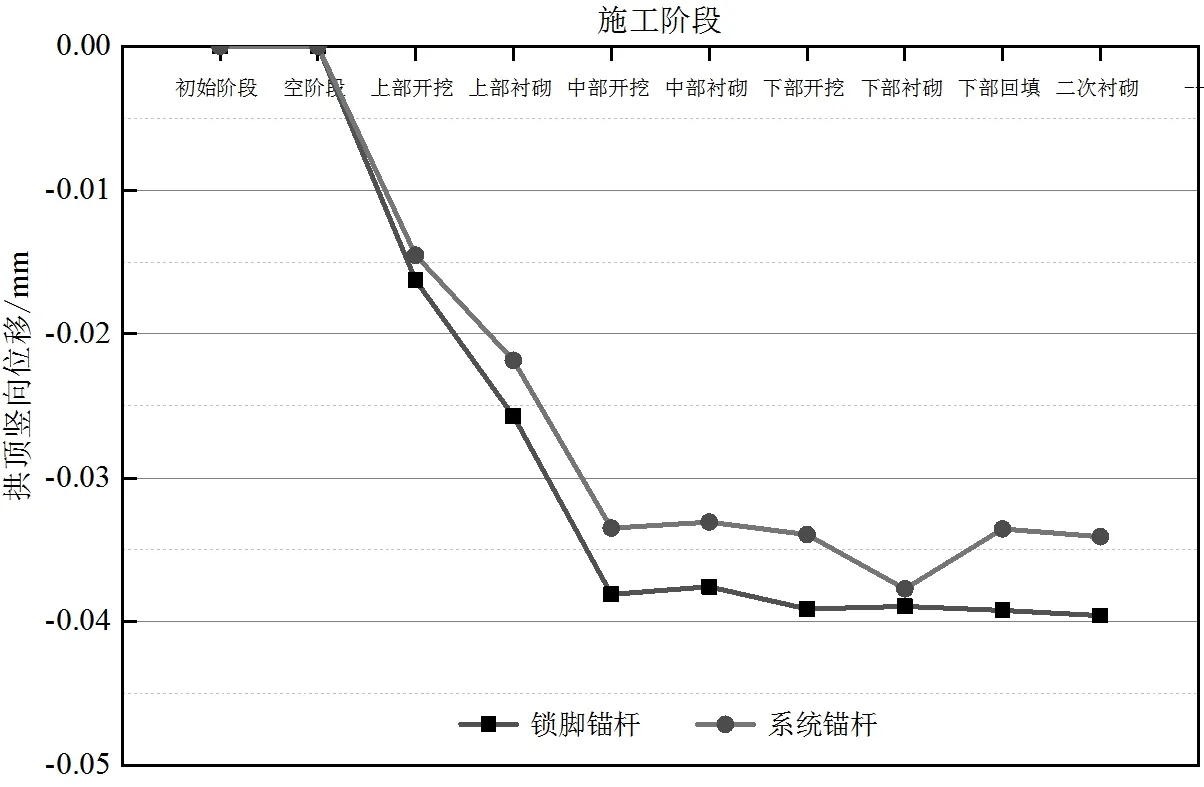
图7 锚索支护的各施工阶段垂直位移变化规律

从图7可以看出系统锚杆支护和锁脚锚杆支护的垂直位移的变化规律，各施工阶段锚杆支护的垂直位移相对于锚索支护较小，但都满足设计要求。从图7可以发现，采用锚杆支护产生最大垂直位移为−0.034 2 mm，而采用锚索支护产生的最大垂直位移为−0.039 4 mm，锁脚锚杆支护和锚杆支护都满足设计要求，从经济的角度出发，系统锚杆的数量和用材要比锁脚锚杆多；因此使用锚索更加经济适用。

3 结论

该文通过有限元软件对某高速公路隧道所采用的两种支护方式进行对比分析，研究锁脚锚杆支护和系统锚杆支护在满足承载要求和变形要求的前提下更经济适用。根据模拟结果可以得到以下结论：

（1）根据模拟结果发现，锚杆支护和锁脚锚杆支护下的拱顶最大位移和隧道断面最大垂直位移均能达到了设计要求，但锁脚锚杆的材料用量远小于系统锚杆较为经济。

（2）从发生最大的位移的位置，可以看出系统锚杆支护最大位移发生的位置在拱顶和仰拱处，而锁脚锚杆支护产生的最大位移在锁脚锚杆支护的另一端。对比产生最大位移的位置发现，锁脚锚杆支护另一端的位移相对于发生在拱顶和仰拱的位置对隧道的影响较小，而发生在锁脚支护另一端的位移对正常的施工和运行没有较大的影响，发生在拱顶和仰拱的位置会直接影响施工和隧道的正常运行。