穿孔机毛管壁厚精度优化模型开发

魏银东

（靖江特殊钢有限公司，江苏 靖江 214500）

对于热轧无缝钢管生产，已有大量研究表明：穿孔后毛管的壁厚偏差无法通过后续的轧管工序完全消除[1]。因此，钢管行业内已对毛管壁厚精度的影响因素进行大量研究[2-9]，其中与穿孔工艺密切相关的为孔型间隙均匀性。该孔型间隙由穿孔机顶头辗轧段与轧辊出口锥段构成，由于穿孔机轧辊布置有送进角，锥形辊穿孔机还有辗轧角，因此该间隙呈现出较复杂的空间几何问题。已有文献提出过该问题的解析算法或经验公式[10-11]，但由于进行了大量近似与简化，损失了计算精度。更为重要的是，这些研究主要基于纯几何的计算，在实际生产过程中，由于设备弹跳和生产调整等原因，顶头的前伸量会明显偏离设计顶头辗轧段时的数值，导致孔型间隙均匀性降低。现针对该种情况，提出送进角补偿方法，并将该功能融合在模型软件中，从而可更持续稳定地保障毛管壁厚精度。

1 孔型间隙算法与顶头辗轧段优化

（1）轧辊辊面方程。直角坐标系定义如下：原点是轧辊孔喉在轧制线上的对应点；X轴是沿轧制线方向，正方向定义为穿孔机入口指向出口的方向；Y轴为轧辊布置在Y轴方向上；Z轴为导卫布置在Z轴方向上。轧辊的辊面方程为：

式中α——送进角，是轧辊轴线在xoz面上的投影与轧制线之间的夹角，（°）；

φ——辗轧角，是轧辊轴线在xoy面上的投影与轧制线之间的夹角，（°）；

β1，β2——轧辊入口锥角和出口锥角，（°）；

D，B——轧辊直径和间距，mm。

需要特别注意的是，式中β并不等于轧辊出入口锥角，定义为：对于轧辊入口锥锥面，β=-（φ+β1）；对于轧辊出口锥锥面，β=-（φ-β2）。这样定义为了使轧辊辊面方程适应入口锥面、出口锥面、锥形辊、桶形辊等各种情况的需要。

（2）轧辊截线方程。用任意垂直于轧制线的截面x=t去截轧辊辊面，可得到形状类似于椭圆的封闭截线，如图1所示，该截线方程为：

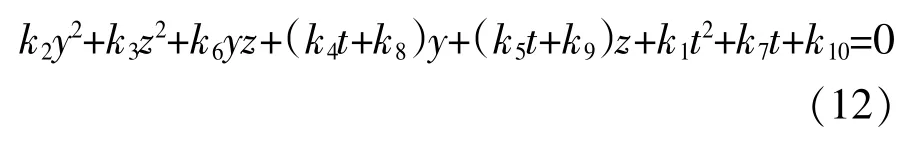
（3）轧辊开度R（t）。

如图1所示，轧辊截线上距离轧制线最近的一点定义为M（t，y，z），则对应于X=t位置，轧辊的开度R（t）可表示为：

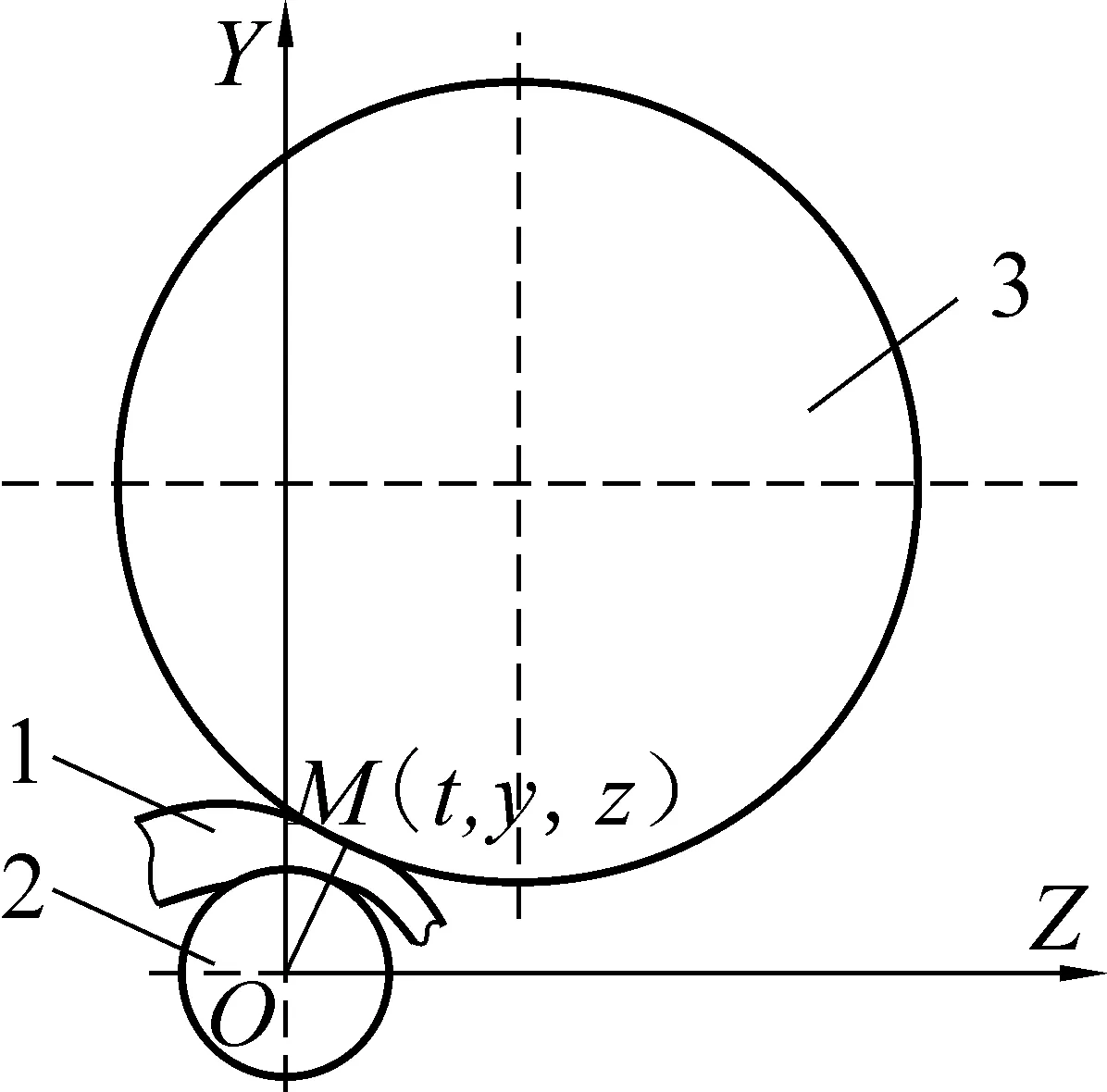
图1 截面x=t内轧辊、顶头、轧件关系示意

轧辊在X=t位置的实际锥角βt可表示为：

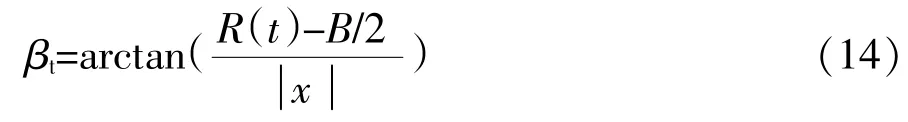
对于M（t，y，z），可以使用数值方法获得十分精确的求解，该数值方法利用计算机程序来实现，其基本逻辑如图2所示。其中，截线方程（12）代入Z值后，可整理为关于Y的二次方程（15）：

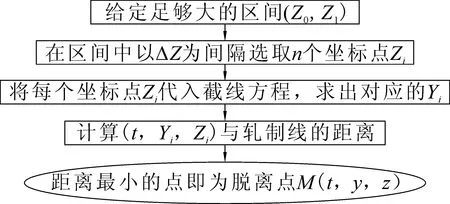
图2 数值方法基本逻辑示意

该数值方法用计算机来完成，只要选取的间隔ΔZ足够小，就能够获得十分精确的数值解。

（4）孔型间隙Δ（t）。孔型间隙沿轧制线（X轴）的变化曲线为：

其中，r（t）为X=t截面内顶头的半径，顶头是以X轴为旋转轴的回转体，顶头母线即对应曲线r（t）。在设计顶头时，可通过优化顶头辗轧段曲线r（t），控制孔型间隙均匀性。

2 送进角补偿方法

在实际穿孔过程中，顶头承受轴向力，顶杆发生弹性变形，导致顶头后移，偏离设计时所预定的位置，进而影响孔型间隙的均匀性。由于对于不同规格、钢种、温度，轴向力、顶头后移距离均不相同；因此在顶头设计阶段，无法通过预先补偿适应所有工况。在实际生产时，为适应规格和钢种的变化，操作工也会人为地前移或后移顶头，在总压下率不变的情况下以控制总压下率和顶前压下率，这同样导致孔型间隙均匀性的降低。

针对该种情况，在顶头形状已确定的情况下，通过现场调整送进角，补偿顶头移位产生的偏差，以保证在各种工况下孔型间隙最优。送进角的调整量通过寻优算法获得，其基本逻辑如图3所示。

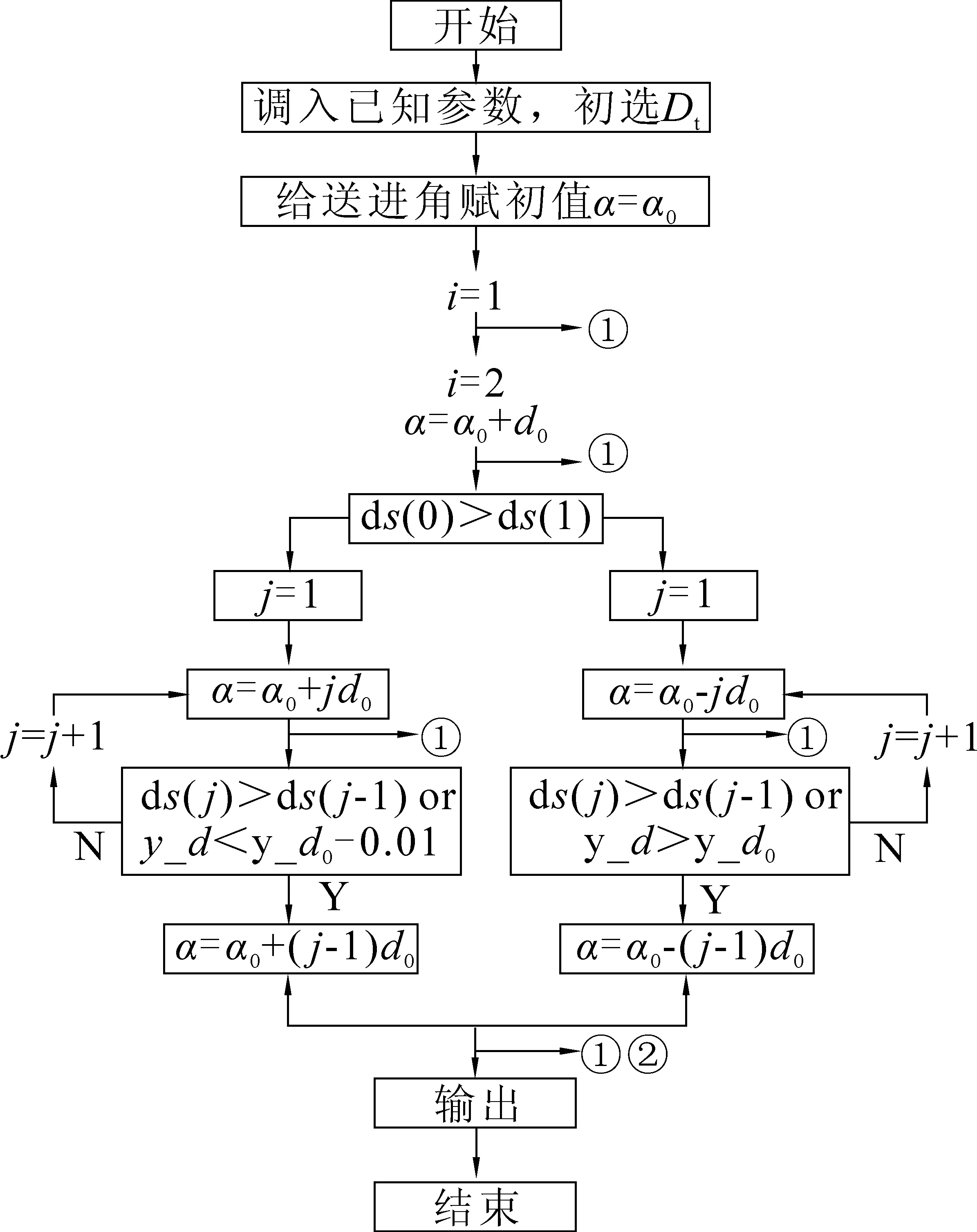
图3 送进角补偿方法基本逻辑

基于该算法，开发了穿孔机工艺调整参数计算软件，界面如图4所示，可根据不同规格、钢种的弹跳量和顶头前伸量参数，自动优化送进角，以获得尽可能均匀的孔型间隙。

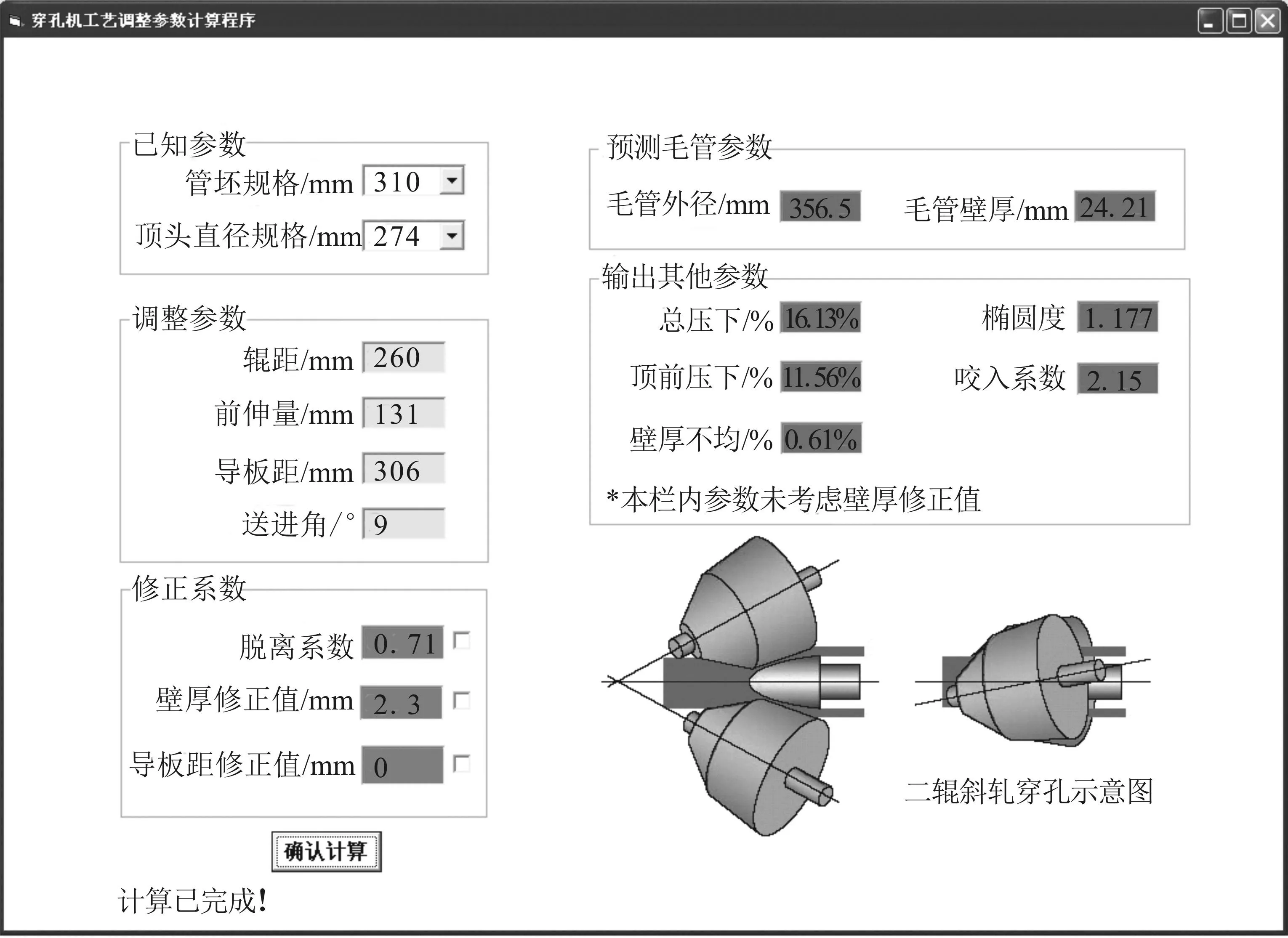
图4 穿孔机工艺调整参数计算软件界面

3 应用情况

使用本研究成果，对穿孔机顶头和送进角进行优化，并应用于现场实际生产。对其中多个规格的毛管进行抽检，壁厚测量数据见表1。分析数据后可知：优化过的顶头和设定参数，可以保证毛管壁厚公差在±4%以内（不计管端）。

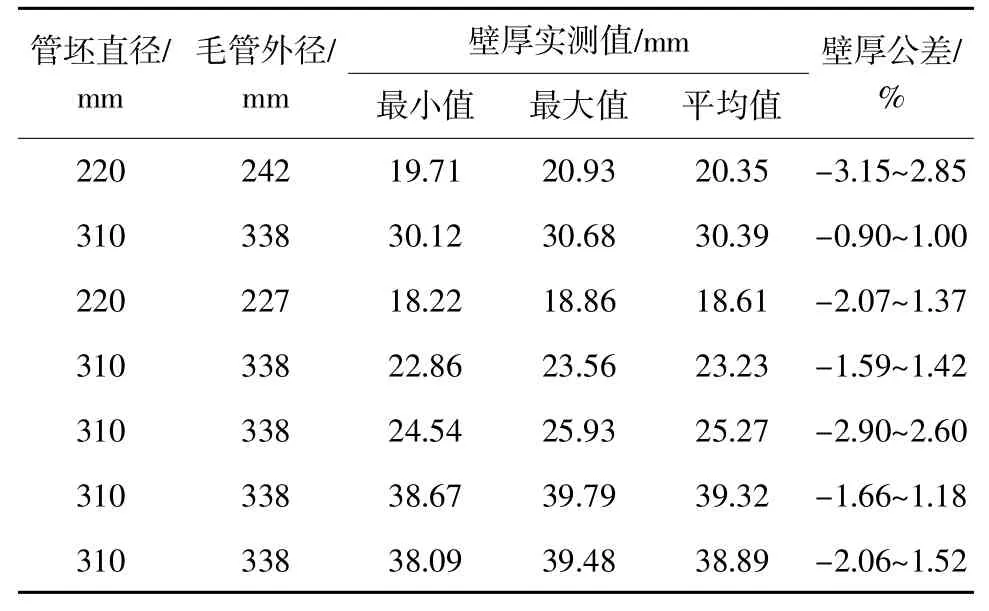
表1 不同规格毛管壁厚实测数据

4 结语

（1）以计算机数值算法为基础，提出一种精确计算穿孔机轧辊与顶头间隙的方法，可用于优化顶头辗轧段设计。

（2）针对实际生产中设备弹跳、人工调整等因素，为提高孔型间隙均匀性，提出通过调整送进角，以补偿顶头位置变动带来的影响的操作方法。

（3）应用所述的方法，可获得较高壁厚精度的毛管，毛管壁厚公差在±4%。