基于多维模糊映射AP优化的WLAN室内定位方法

杨小龙，李欣玥，周 牧，王 勇，何 维

(1.重庆邮电大学通信与信息工程学院，重庆 400065；2.重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065)

1 引言

随着物联网技术的蓬勃发展和各种移动智能设备的广泛应用，基于位置的服务（Location-Based Service，LBS）在各种日常活动中提供着越来越多的便捷，如人员导航指引、仓储位置管理和灾害应急救援等.因此，如何保证LBS 的可靠性和便捷性已成为近年来国内外相关研究人员关注的焦点.然而，在实际的室内环境中，由于存在墙体、家具等障碍物遮挡和复杂的人员干扰，室内无线信号在传播过程中一般会受到严重的信号强度衰减和多径效应影响，从而限制了室内定位技术的发展.当下，较为典型的室内位置估计技术有超宽带（Ultra Wide Band，UWB）［1］、红 外（Infrared Ray，IR）［2］、射频识别（Radio Frequency IDentification，RFID）［3］、蓝牙（Bluetooth）［4］、超声波（Ultrasonic Wave，UW）［5］、ZigBee［6］、可见光［7］和无线局域网（Wireless Local Area Network，WLAN）［8］室内位置估计技术.然而，上述技术大多需要额外的硬件设备以及较大的系统部署开销，从而导致其难以得到广泛的推广应用.相较而言，WLAN 室内定位技术因其具有易部署、成本低和通信覆盖范围广等特点［9］，已逐步成为室内位置估计技术发展的重要趋势.

在无需特殊硬件要求（如利用半波长间隔的阵列天线来实现基于信道状态信息（Channel State Information，CSI）的超分辨角度估计［10］）的条件下，WLAN 室内定位方法主要有传播模型法和位置指纹法.前者通过信号传播模型刻画接收信号强度（Received Signal Strength，RSS）与信号传播距离之间的关系，并基于目标所在场景中位置已知的WLAN 接入点（Access Point，AP）和利用如近似三角内点检验（Approximate Point-intriangulation Test，APIT）［11］等几何位置坐标估算方法来完成移动终端的位置分析，但由于在遮挡物较多的室内环境中信号传播通常存在非视距（Non-Line-Of-Sight，NLOS）的情况［12］，所以如何建立能够准确描述室内RSS信号特征的信号传播模型是一个非常复杂的问题［13］.相对而言，位置指纹法无需构造信号传播模型，其主要包含离线和在线两个过程.在离线阶段，通常需要在目标环境中提前标记多个位置已知的参考点（Reference Point，RP），并提取这些RP 处来自不同AP 的接收信号特征，进而利用这些RSS 特征及对应的RP 位置构建离线位置坐标数据库；而在在线阶段，则将目标处提取的当前测量的接收信号特征与离线位置坐标数据库进行比对，并利用如K 近邻（K-Nearest Neighbor，KNN）［14］等邻近匹配算法来估计目标位置［15］.

近年来，国内外学者关于WLAN 室内定位方法的研究有了进一步发展.如文献［16］提出了一种用于WLAN 室内定位的T检验样本容量优化方法，其利用操作特征（Operating Characteristics，OC）函数来分析定位性能与RSS 样本容量之间的关系，以降低位置指纹数据的采集开销；文献［17］利用动态区域划分机制来构建用于WLAN 室内定位的基于相对RSS 特征的快速位置指纹数据库.上述两种方法虽能有效降低位置坐标数据库的建库成本，但没有考虑来自不同AP 的RSS 特征位置分辨力的差异性，从而导致定位精度不高且定位效率较低.为此，考虑室内RSS特征的多样性和噪声的随机性问题，文献［18］利用模糊隶属函数计算RSS标准差，虽然该方法在一定程度上表征了信号分布的特点，但得到的RSS 特征难以有效反映室内环境中信号变化的复杂性和多样性.此外，文献［19］提出了Maxlifd 协作定位方法，其通过联合最大似然估计融合离线指纹和指纹间互距离先验信息，同时结合半定规划（Semi-Definite Program，SDP）方法对目标进行定位，然而，该方法仅选择单一类型的RSS 特征用于定位且在线阶段的计算开销较大，故在实际应用中受到一定限制.

对上述问题，本文提出一种基于多维模糊映射AP优化的WLAN 室内定位方法，如图1 所示.具体而言，考虑选择具有较差位置分辨力的RSS 特征和单一类型RSS特征用于定位会导致定位精度和效率的下降，本文方法在离线阶段提取多维RSS 特征以计算AP 信息增益比及相应的离线模糊隶属度，并利用模糊关系方程求解多维RSS 特征模糊权重；而在在线阶段，则通过多维模糊映射构造模糊判定矩阵并计算AP 在线模糊隶属度，同时结合KNN算法完成对目标的位置坐标估算.

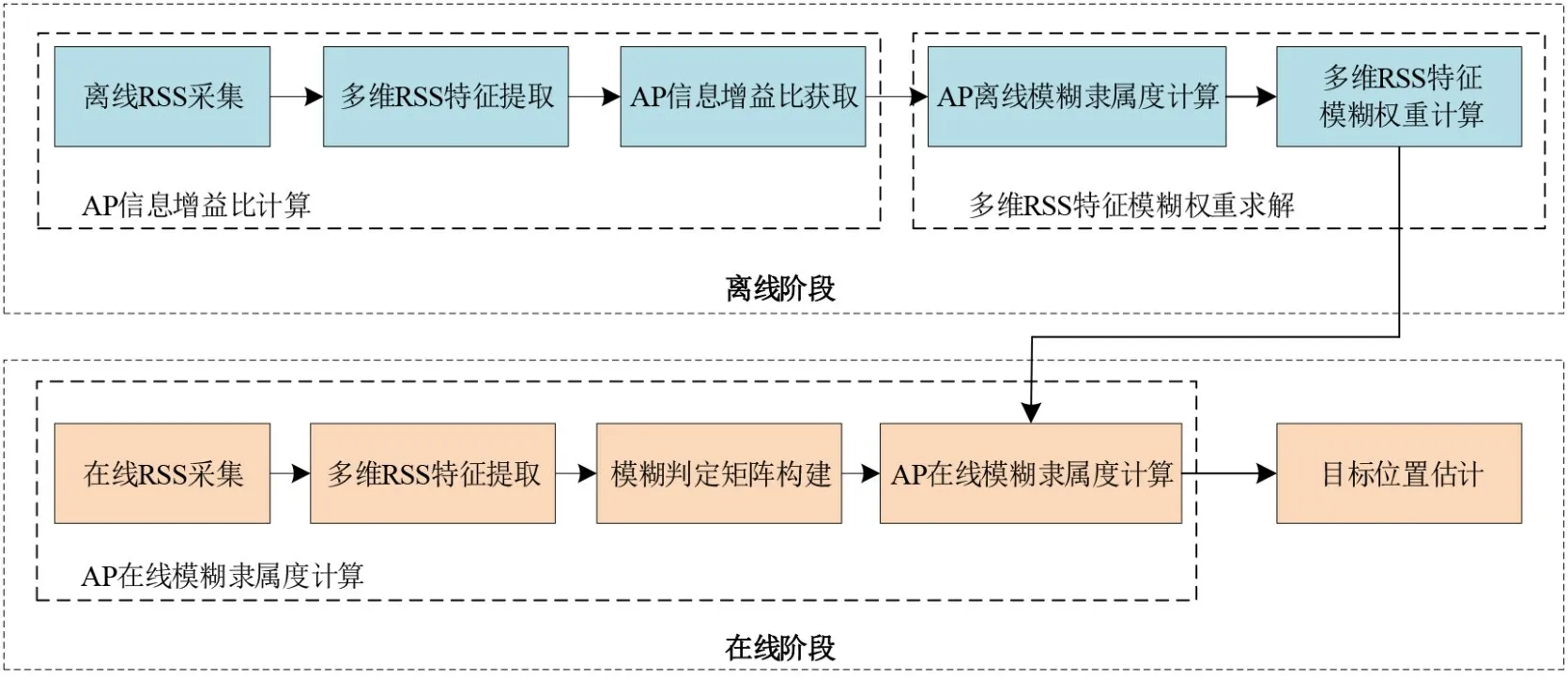
图1 系统流程图

2 离线阶段

2.1 AP信息增益比计算

首先，假设离线阶段目标环境中有n个AP和m个RP，对于n个AP 发射信号，在m个RP 处进行多次信号采集以得到RSS 强度数据集.RSS 序列表示为RS S1，…，RS Sj，…，RS Sm，其中，RS Sj表示在第j(j=1，2，…，m)个RP 处测量到的来源于n个AP 的信号数据序列，RS Sj=()rss1j，rss2j，…，rssnj，rssij表示在第j个RP 处测量的来源于i(i=1，2，…，n)个AP 的信号强度.基于此，可构造RSS集合：

再次，根据Zoff估算目标所在场景中全体参考点关于第i个AP的不确定度，如式（4）所示：

其中，ψs=(，…，)为目标所在场景中全体AP 对于第s个离线接收信号数据特征的信息增益比.此时，值越大，表明在已知第i个AP 的第s个离线接收信号数据特征时，目标所在场景中全体参考点分布的确定度提高越多.

2.2 多维RSS特征模糊权重求解

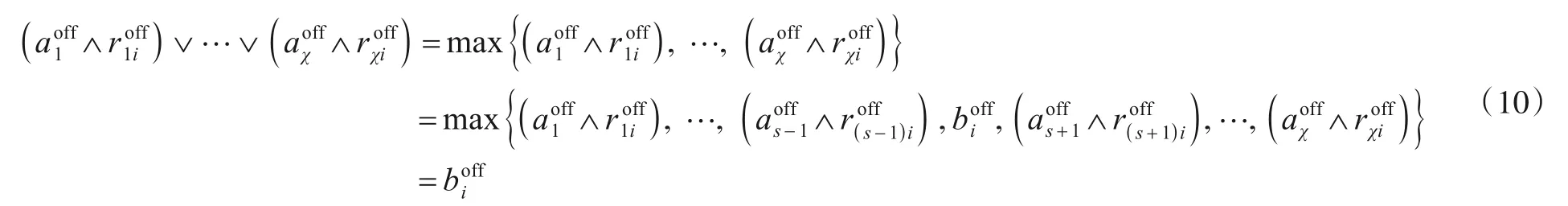
3 在线阶段

3.1 AP在线模糊隶属度计算

最后，由于离线过程得到的多维接收信号数据特征模糊权重向量Aoff能够有效刻画室内信号测量的偶然性和随机性，且离线和在线阶段均针对同一物理环境，于是可根据Aoff和Ronli，建立关于在线接收信号数据特征的模糊关系方程为

3.2 目标位置估计

根据式（18）得到的AP 在线模糊隶属度，计算测试环境中第ω(ω=1，…，w)个待定位目标位置与第j个RP的RSS特征指纹之间的距离Djω，Djω=，其中分别表示在第ω个待定位目标位置和第j个参考点处接收到的来自第i个AP 的第s个RSS 特征均值.然后，选择具有最小RSS 特征指纹距离的k个RP（即k近邻点）并结合KNN算法实现对目标的物理坐标估算.

4 实验结果

4.1 实验环境

在56.93 m×20.08 m 的室内环境中，选择2 个走廊区域和一个房间区域作为目标区域（即图2 中区域1，2和3）.在目标环境中部署8 个AP（即AP1，AP2，AP3，AP4，AP5，AP6，AP7和AP8），并均匀标记88个RP和25个待定位目标位置.离线阶段，在每个RP 处依次采集10 s的RSS样本信号，并在不同时段分别进行多次信号采集以构建离线指纹数据库.在线阶段，在待定位目标位置处采集5 s 的RSS 样本信号用于位置估计，且上述2个阶段的采集速率均为1 Hz.

图2 实验环境结构图

4.2 参数讨论

在测试实验中，为了便于区分和讨论，将所部署的AP 根据在线模糊隶属度进行降序排列，并用λ表示用于定位的AP的在线模糊隶属度之和.在此基础上，图3给出了根据AP 在线模糊隶属度从大到小依次选取单个AP 用于定位的平均定位误差.由图3 可知，随着AP在线模糊隶属度的增大，每个区域的平均定位误差均呈下降趋势，这表明具有较大在线模糊隶属度的AP 对定位精度的贡献更大.

图3 选择具有不同在线模糊隶属度的AP用于定位的平均定位误差

为了更加清晰地说明AP 在线模糊隶属度对定位精度的有益影响，图4 给出了当AP 数量分别为2，3，4和5，并随机选取不同的λ值对应的AP用于定位时的定位误差.从图4可以看出，随着λ值的增大，系统定位误差呈下降趋势，以区域1 的定位误差为例，当用于定位的AP 个数分别为2，3，4和5时，随着λ从最小值增加至最大值，定位误差分别降低了5.01 m，3.98 m，3.81 m和4.03 m.

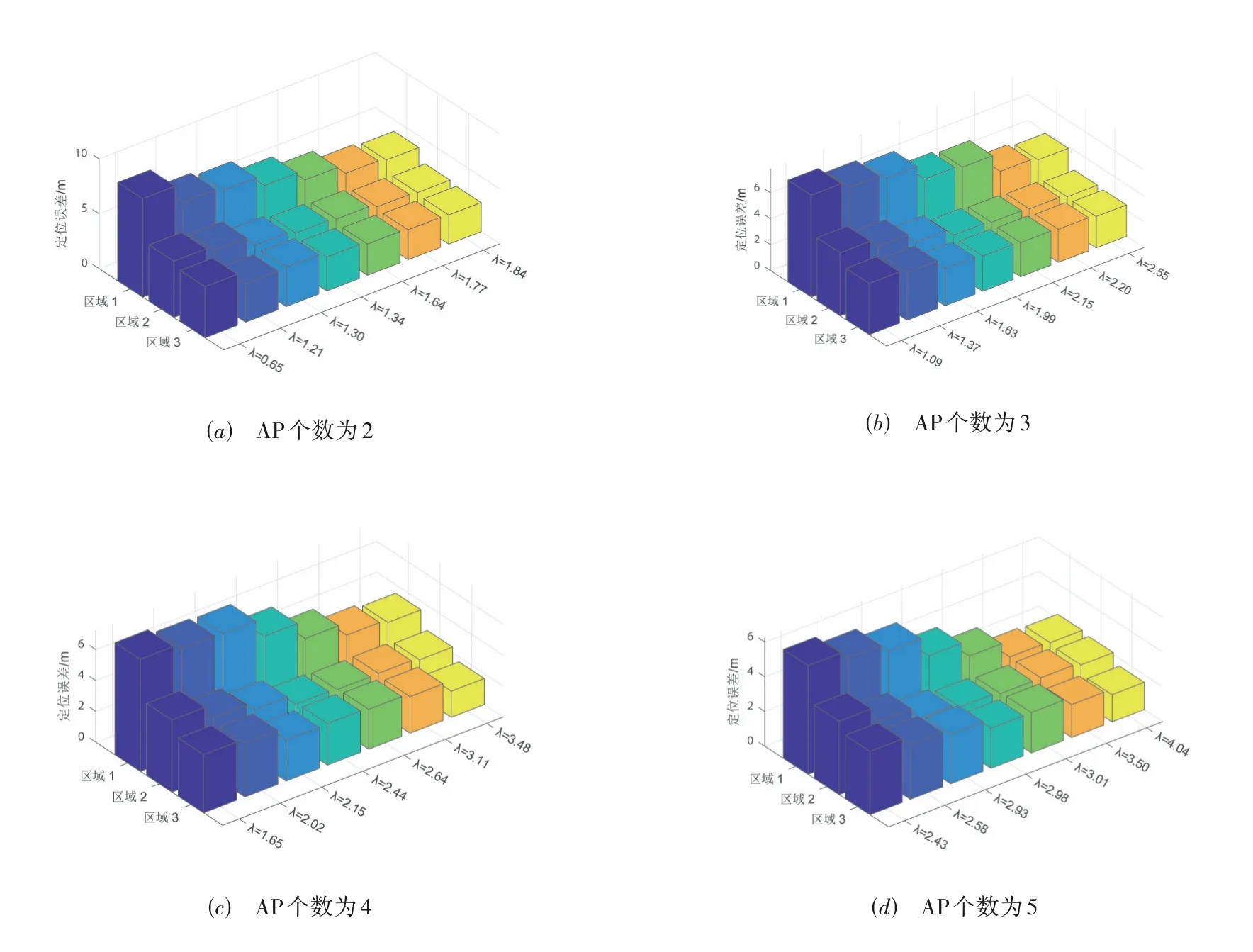
图4 不同AP个数与λ值条件下的平均定位误差

此外，为了进一步验证AP 在线模糊隶属度在AP优化方面的有效性，图5 给出了随λ值的增大平均定位误差的变化情况.由图5 可知，当选择具有最大在线模糊隶属度（即λ=0.93）的AP 用于定位时，平均定位误差为5.26 m，而当选择前2，3和4个具有较大在线模糊隶属度的AP 用于定位时，平均定位误差分别降低1.19 m、0.79 m和0.83 m，但随着AP 数逐渐增大到5，6，7和8时，平均定位误差分别降低仅0.26 m，0.14 m，0.12 m和0.02 m，即平均定位误差呈收敛趋势.因此，选择具有较大在线模糊隶属度的AP 用于定位不仅能够实现较高的定位精度，还可有效降低在线阶段的定位计算开销（即选择较少的AP用于定位）.

图5 不同λ值条件下的平均定位误差

4.3 定位计算开销讨论

图6 比较了在不同λ值条件下的定位计算开销（即对所有测试点进行位置估计所需的时间开销）.由图可知，随着λ值的增大（即用于定位的AP 数的增加），各个区域的定位计算开销均呈上升趋势，以λ值从0.93增大到5.13 为例，区域1，2和3 的定位计算开销分别增加了7.06 s，7.03 s和5.81 s.此外，相较于区域2和3，区域1 内的障碍物较少且测试点较多，故不同位置处RSS 信号差异性较小且较为复杂，从而需要较大的时间开销来计算AP 的在线模糊隶属度以选择用于定位的最优AP.

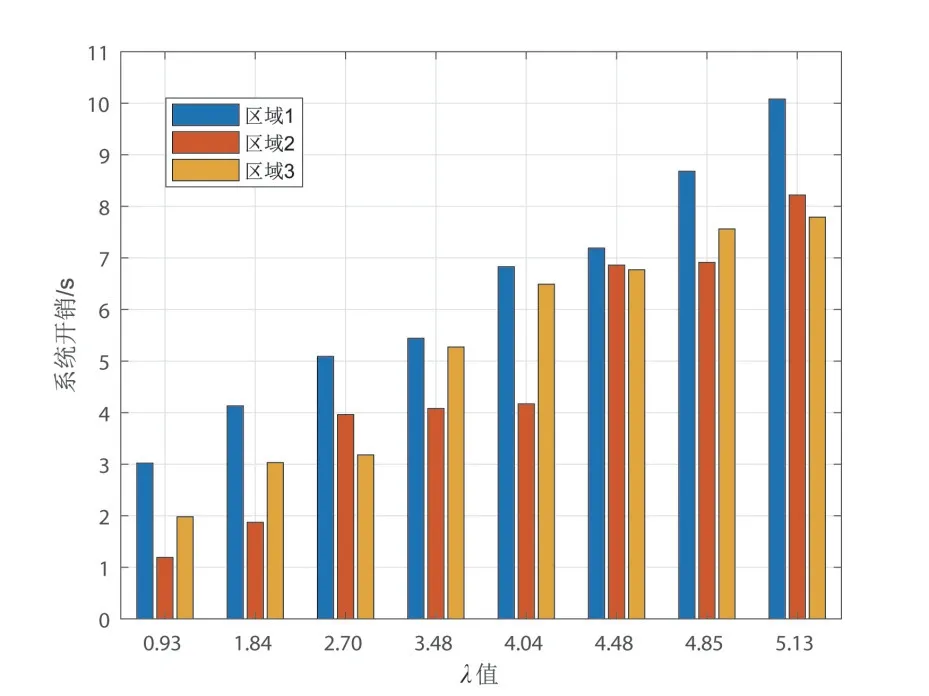
图6 不同λ值条件下的定位计算开销

图7给出了本文方法以及现有的4 种具有较低开销的定位方法，即T 检验法［16］、最大似然法［21］、信息增益法［22］和Max-Mean 法［23］的定位计算开销.由图7可知，T 检验法的定位计算开销最大，其在区域1，2和3 的开销分别为10.83 s，8.94 s和7.58 s，而本文方法相较于T 检验法开销最高减少了4.12 s.此外，Max-Mean 法的定位计算开销最小，原因在于其计算过程较为简单，即根据不同参考点处接收到来自每个AP的RSS 均值大小选择合适的AP 用于定位，但由图8可知Max-Mean 法的定位精度不高，原因在于其AP选择过程中仅考虑单一的RSS 特征（即RSS 均值）作为依据，而忽略了RSS 特征多样性对定位性能的影响.

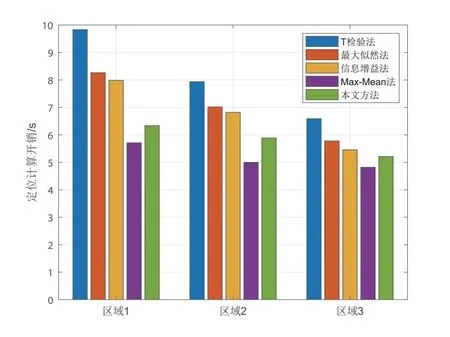
图7 不同定位方法的定位计算开销

4.4 定位结果讨论

图8给出了选择不同AP用于定位的平均定位误差分位图.由图8 可知，与信息增益法（即选择具有较大信息增益的多个AP）［22］、Max-Mean 法（即选择具有较大RSS 均值的多个AP）［23］、全AP法（即选择全体AP）［24］、最强AP 法（即选择具有最强RSS 的AP）［24］和最大方差法（即选择具有最大RSS 方差的AP）［24］相比，本文方法在空旷和复杂室内环境中均具有稳定且最小的平均定位误差，其原因在于本文方法选择全体AP 用于定位并利用在线RSS 特征的模糊关系方程计算AP 在线模糊隶属度，然后通过对具有较大在线模糊隶属度的AP 分配较大的RSS 特征指纹距离权重来提高定位精度.

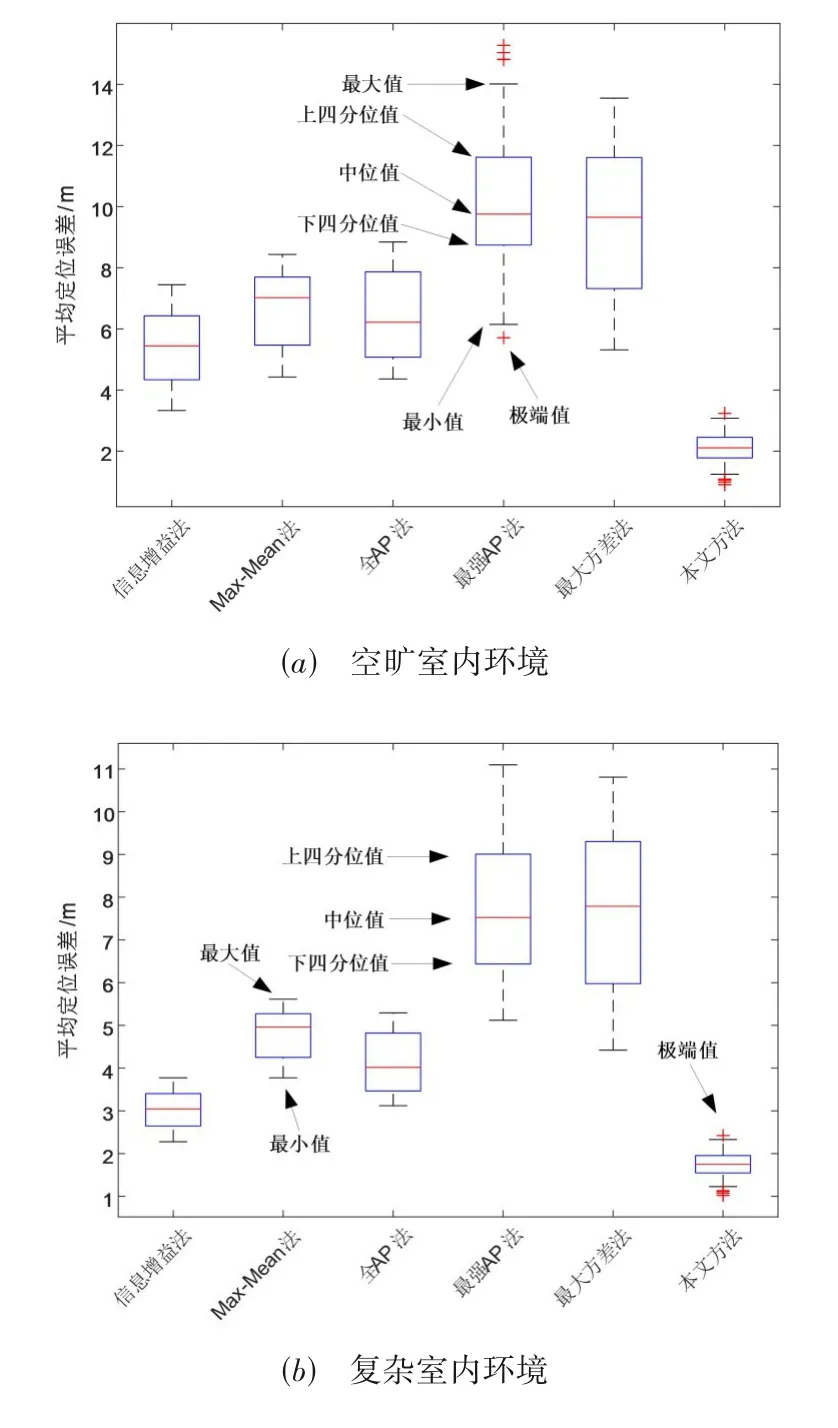
图8 选择不同AP用于定位的平均定位误差分位图

图9 给出了本文方法以及现有的4 种常用定位方法，即KNN 法［14］、T 检验法［16］、最大似然法［21］和贝叶斯法［25］的误差累积分布函数（Cumulative Distribution Function，CDF）.由图9 可知，本文所提位置估计算法定位误差小于等于4 m 的置信概率是91.91%，高于其他4 种方法的76.21%（KNN 法）、82.38%（T 检验法）、73.28%（最大似然法）和67.17%（贝叶斯法）.为了进一步验证本文所提多维模糊映射AP 优化方法对定位精度的有益影响，图10 比较了5 种基本定位方法，即均值KNN 法［12］、最大似然法［21］、贝叶斯法［25］、加权最小二乘法［26］和中值KNN 法［27］在AP 优化前后的平均定位误差.可以看出，通过对AP 进行优化能够显著提高定位精度，从而验证了本文所提AP 优化方法的有效性.

图9 不同定位方法的误差CDF

图10 AP优化前后不同定位方法的平均定位误差

5 结论

针对传统WLAN 指纹定位方法中常常忽略RSS 特征多样性以及来自不同AP 的接收信号数据特征位置分辨力的差异性问题，本文提出了一种基于多维模糊映射AP优化的WLAN 室内定位方法.该方法在离线阶段多次采集接收信号数据以得到离线多维接收信号数据特征，并由此计算AP 信息增益比及相应的离线模糊隶属度，同时通过模糊关系方程求解各个接收信号数据特征的模糊权重，然后根据在线接收信号数据特征建立模糊判定矩阵并计算AP 在线模糊隶属度，并结合KNN算法对目标进行定位.此外，本文通过实验验证了所提方法在选择较大在线模糊隶属度的AP用于定位的条件下，不仅达到了较高的定位精度，还显著减小了在线过程的目标位置估算开销.基于此，如何实现室内目标运动过程中的AP动态优化将作为下一步主要工作.