基于双观测器的多电机卷绕系统切换滑模控制

贺志浩，于海生

(青岛大学自动化学院，山东青岛 266071)

0 前言

多电机卷绕系统在纺织、造纸、机器人控制、流水线生产等领域中应用广泛，而永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)具有功率密度大、效率高、输出转矩大等优点，常作为多电机卷绕系统的驱动机构。系统在设计时要同时确保对电机转速和系统张力的精准控制。但是，PMSM是强耦合、模型不确定的非线性系统，在实际运行中，系统容易受到参数摄动和负载扰动的影响。因此，如何提高多电机卷绕系统的性能十分重要。

在多电机卷绕系统中，对单台电机的精确控制是实现系统整体性能的基础。目前，对于PMSM的控制，国内外学者做了许多研究。文献[7]中提出了一种自适应反步控制方法，采用负载转矩自适应律近似一个非线性的降阶扰动观测器，该方法提高了系统的抗干扰能力，但是系统的稳态性能还需进一步提高。文献[8]中采用了端口受控哈密顿控制方法，建立了PMSM的哈密顿模型，通过反馈镇定原理设计控制器；该方法提高了系统的稳态性能，但是响应速度较慢。文献[9]中采用了带有快速趋近律的滑模控制器，提高了系统的响应速度，但是系统抖振较大。与传统的线性滑模相比，非奇异快速终端滑模具有更高的稳态跟踪精度和更强的抗干扰能力，且抖振较小，目前应用广泛。

对于系统的张力，目前有许多控制方法，最简单的方法是采用PI控制器来实现对系统张力的控制，但是该方法的控制效果较差。为了提高张力控制精度，文献[12]设计了H张力控制器，提高了系统的抗干扰能力；文献[13]则设计了张力滑模控制器和滑模观测器，实现了张力系统的无传感器控制。与PI控制相比，以上控制方法提高了张力的控制精度。但是，以上方法没有实现张力和速度的完全解耦，系统受到的耦合影响较大。为了解决这一问题，文献[14]利用反馈线性化控制系统实现了系统解耦，降低了子系统间的耦合干扰；文献[15-16]采用了离散控制方法，设计了一种对子系统的耦合干扰具有较强抑制作用的协调控制策略；文献[17]则是对系统的张力环和速度环分别设计了自抗扰控制器，实现了张力和速度的完全解耦。然而，以上控制方法都没有针对参数摄动问题提出一个较好的解决方案。近年来，国内外学者对非线性扰动观测器做了大量研究，结果表明：可以通过设计非线性扰动观测器来得到参数摄动的估计值，并将其用于前馈补偿控制，该方法对参数摄动具有较好的抑制效果。

针对以上研究中存在的问题，本文作者研究了强耦合、易受参数摄动和负载扰动影响的多电机卷绕系统。为了实现张力和速度的完全解耦，对系统张力环和PMSM分别设计控制器。其中，为张力环设计了自适应切换滑模控制器，切换函数可以使系统状态更快到达滑模面，提高了系统的响应速度和跟踪精度，并设计张力观测器来精确观测系统中张力的大小；PMSM采用非奇异快速终端滑模和非线性扰动观测器的复合控制方法，提高了系统的鲁棒性和抗干扰能力。最后通过仿真实验验证了所提控制策略的有效性。

1 多电机卷绕系统的数学模型

本文作者研究了由3台PMSM构成的多电机卷绕系统，其结构如图1所示。3台电机分别与3个滚筒相连，中间通过15∶1的减速器减速后驱动滚筒运转；3个滚筒通过一条皮带进行连接，相邻滚筒之间的浮动滚筒用于产生皮带张力。

图1 3电机卷绕系统模型

根据虎克定律，电机1与电机2之间的张力为

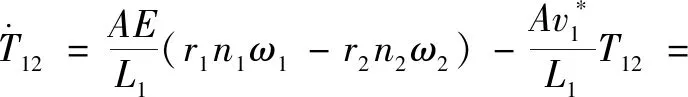
(1)

电机2与电机3之间的张力为

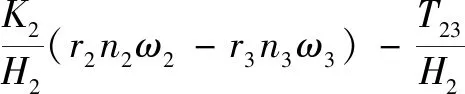
(2)

对于PMSM,在d-q轴旋转坐标系下的数学模型为

(3)

=15[(-)+]

(4)

式中:、分别为d、q轴定子电感；、分别为d、q轴定子电流；、分别为d、q轴定子电压；为定子电阻；为机械角速度；为电机的极对数；为永磁体产生的磁链；为转动惯量；为摩擦因数；为电机的电磁转矩；、为由于参数摄动所引起的扰动；为张力力矩。其中，、可表示为

(5)

式中：Δ=-；Δ=-；Δ=-;Δ=-。其中:、、、代表参数的实时值。

在系统中，3台PMSM的是不相同的，可分别表示为

(6)

2 多电机卷绕系统的控制框图

由3台PMSM组成的多电机卷绕系统控制框图如图2所示。

图2 3台PMSM卷绕系统控制框图

3 第i台PMSM的控制策略

图3 第i台PMSM矢量控制系统框图

3.1 非奇异快速终端滑模控制器的设计

对于第台PMSM，定义

(7)

对式(7)求导，根据d=q=，将式(4)代入得

(8)

分别选取非奇异快速终端滑模面和趋近律为

(9)

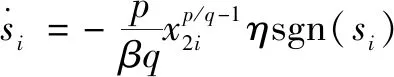
(10)

式中：1<<2且、均为正奇数，>0，>0，>0，>1。

对式(9)求导，并将式(8)和式(10)代入可得速度环非奇异快速终端滑模控制律为

(11)

定义d轴和q轴的电流误差为

(12)

为了得到稳定的反馈，令

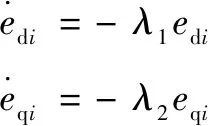
(13)

式中：>0，>0。

将式(3)和式(12)代入式(13)可得电流环控制器为

(14)

定义Lyapunov函数为

(15)

对上式求导，并将式(10)和式(13)代入可得

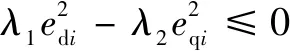
(16)

由Lyapunov稳定性定理可知，非奇异快速终端滑模控制器是渐近稳定的。

3.2 非线性扰动观测器的设计

为了降低参数摄动对系统的影响，设计非线性扰动观测器，对于如下非线性系统

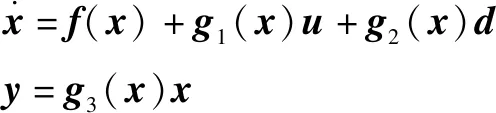
(17)

其中：为系统存在的扰动。该系统的非线性扰动观测器可设计为

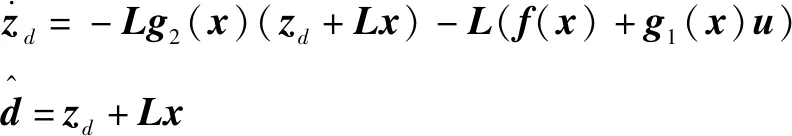
(18)

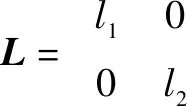
(19)

对于第台PMSM，根据式(3)和式(17)可得：

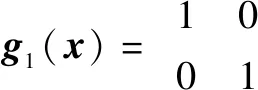
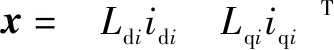
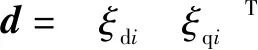
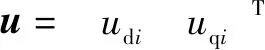
扰动的估计误差为

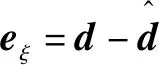
(20)

选取Lyapunov函数为

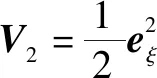
(21)

对上式求导，并将式(17)和式(18)代入可得

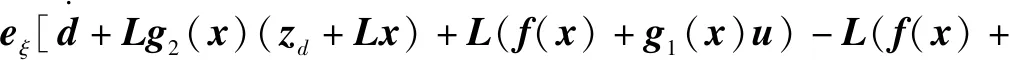
(22)

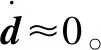
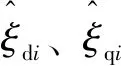
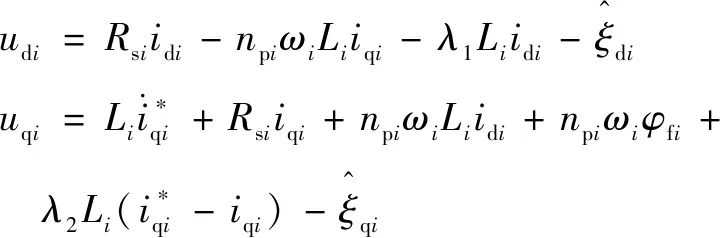
(23)

4 系统张力的控制策略

4.1 自适应切换滑模控制器的设计

传统的自适应趋近律为

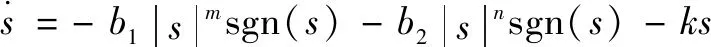
(24)

式中：>1，0<<1，>0，>0，>0。

(25)

切换函数定义为

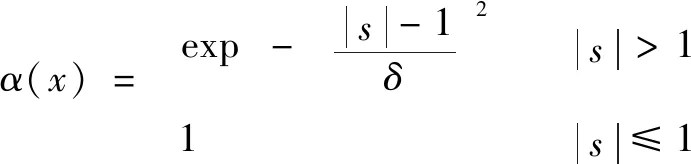
(26)

式中：为尺度参数。

以电机1和电机2之间的张力为例，阐述张力环滑模控制器的设计过程。定义张力误差为

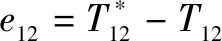
(27)

选取滑模面为

(28)

式中:为常数。

对式(28)求导，并将式(1)代入可得

(29)

采用式(25)的趋近律，可得自适应切换滑模控制器为

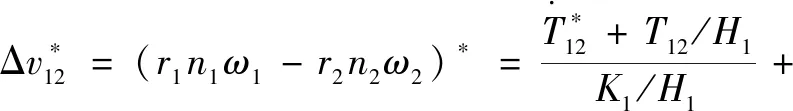
(30)

取Lyapunov函数为

(31)

对式(31)求导，并将式(25)代入可得

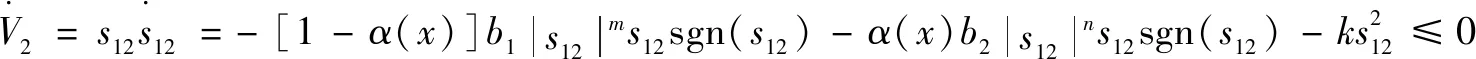
(32)

由Lyapunov稳定性定理可知，自适应切换滑模控制器是渐近稳定的。

4.2 张力观测器的设计

当张力恒定已知时，有

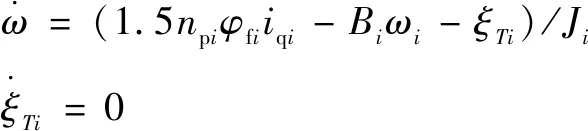
(33)

为了得到张力力矩的估计值，设计张力观测器为

(34)

(35)

加入张力观测器后，式(11)变为

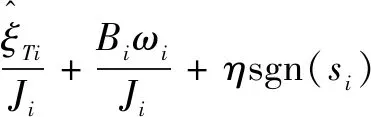
(36)

5 仿真实验分析

为了验证所设计的多电机卷绕系统的性能，采用MATLAB/Simulink对其进行仿真验证。自适应切换滑模控制器参数：==5，=1.3，=0.1，=25，=0.01；非奇异快速终端滑模控制器参数：=200，=11，=9，=7，=2，=3；非线性扰动观测器参数：==10 000；张力观测器参数：=-1 250；电机之间的距离：==1 m；滚筒半径：===0.2 m；横截面积：=5×10m；弹性模量：=3.2×10N/m。表1给出了PMSM的具体参数。

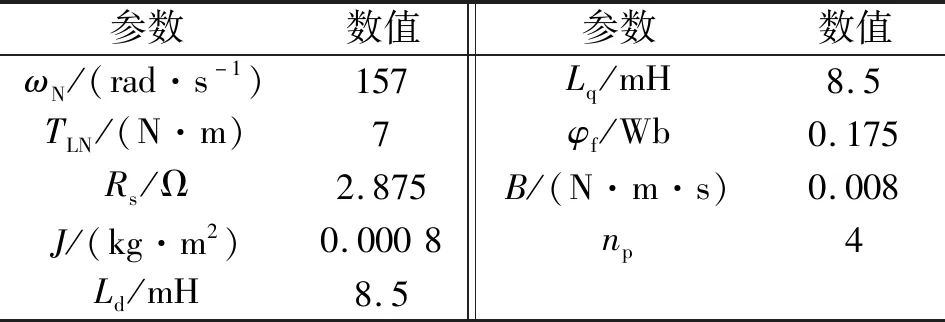
表1 PMSM参数

本文作者设置了3组仿真实验，仿真时间均为=10 s。

从图4和图5可以看出:与自适应滑模和传统线性滑模相比，张力环采用自适应切换滑模控制提高了系统的响应速度和跟踪精度，且系统没有超调；当电机转速变化或者受到负载扰动时，自适应切换滑模的误差更小，恢复时间更快，系统的抗干扰能力得到提高。从图6可以看出张力观测器可以准确观测张力大小，并快速跟踪给定值。

图4 张力环在不同控制策略下的张力响应曲线

图5 张力环在不同控制策略下的误差响应曲线

图6 张力观测器的观测曲线

图7 参数摄动时的张力响应曲线

从图7可以看出:电阻的变化对系统张力的影响较小；在未添加非线性扰动观测器的情况下，系统张力的抖动较大，跟踪精度较低，且当磁链和电感发生摄动时，系统张力的跟踪误差会逐渐变大；添加非线性扰动观测器减小了系统张力的抖动，提高了跟踪精度，且极大降低了磁链和电感摄动的影响。因此，非线性扰动观测器提高了系统的鲁棒性和跟踪精度，并减小了抖动。

图8 4种控制策略下的张力响应曲线

表2 不同控制策略下系统的性能表现

从图8和表2可以看出：与张力环和PMSM均采用PI控制的策略相比，张力环采用自适应切换滑模控制策略提高了系统的跟踪精度；PMSM采用非奇异快速终端滑模和非线性扰动观测器的复合控制策略提高了系统的抗干扰能力，并减小了抖动。

6 结论

提出一种基于双观测器的多电机卷绕系统的切换滑模控制方法。为了实现张力和速度的解耦控制，提高系统的响应速度和跟踪精度，对张力环设计了自适应切换滑模控制器，速度环采用非奇异快速终端滑模控制器。为了减小参数摄动对系统的影响，采用非线性扰动观测器来估计参数摄动，并将估计值用于前馈补偿控制。最后设计张力观测器来观测张力的大小。仿真结果表明，该控制策略具有良好的动态性能和稳态性能，提高了系统的抗干扰能力，且对参数摄动具有较强的鲁棒性。