均匀带电球体激发电场分布解的修正分析
叶 荣,吴显云,曾婷婷
(成都师范学院 物理与工程技术学院,四川 成都 611130)
0 引言
静电场中,均匀带电球体激发电场是最简单的物理模型之一,求解空间各点的电场强度或电场分布是十分重要的问题。常用的方法有利用球面坐标取电荷微元产生的电场的叠加法[1-2],由场强与电势的微分关系计算、由场的微分方程求解[3],和利用高斯定理计算等。其中高斯定理是静电场问题中常用的普遍规律,对于求解具有对称性的电场极为适用。但已有的文献中,均匀带电球体内激发电场的电荷的组成未加以区分,其内外电场强度的连续性问题,也没有比较完善和准确的研究。本文首先从真空中的高斯定理求出的均匀带电球体的电场分布与球面界面两侧法向电场的矛盾出发,理论分析了均匀带电球体激发的静电场的修正表达,最后明确了均匀带电球体激发电场的基本物理模型,并对模型进行了物理解释。
一个均匀带电量为Q 的半径为a 的球体,已有常见解法中是选用最简单的高斯定理求其内外电场分布,即分别在均匀带电球体内和球体外,取一个球面高斯面,如图1 所示[[4-5]。

图1 真空中的高斯定理求出的均匀带电球体的电场
由高斯定理有:
可得到,在r >a 的球体外和r <a 的球体内各点空间,其电场强度E外和E内分别为:

电场强度的方向均沿径向方向。由以上两式可知,在r >a 的球外与r <a 的球内空间的交界面处,也即球表面处的电场强度,无论是由球外的电场表达式(2a)在r 从无穷远趋于r=a,还是由球内的电场表达式(2b)在r 从球心趋于r=a,均可得到相同的结果:

由于内外电场强度的方向均沿径向方向,则在自然坐标系下,交界面两侧的电场强度只有法向分量,而没有切向分量。这表示均匀带电球体内外交界面处的电场强度的法向分量是连续的。这与电磁场的边值关系,界面两侧电场的法向分量是不连续的存在着矛盾[6]。
1 均匀带电球体激发电场的优化修正
均匀带电球体所带电量为Q,即表明电荷是均匀分布在球体内呈体分布的,也即该球体所带净余电荷的净余电量为Q。由此可知,该球体不可能是导体,只能是介质。因为根据静电场中的导体的特征,若导体带有一定电量的电荷,其电荷全部分布在表面上,不可能均匀分布在球体内,其内部也不可能有电场。既然该均匀带电球体为电介质,且可以假定其为各向同性线性均匀介质,则它必定有一个常数电容率ε,且通常大于真空中电容率ε0。其次,未带电荷前,电介质整体是呈电中性的,则所带的净余电荷Q 只能是外来的自由电荷Qf,相应的自由电荷体密度为:

鉴于球体为电介质,在静电场作用下,介质会被极化,因此介质球内和介质球表面会分别存在着呈体分布的极化电荷体密度ρp和呈面分布的极化电荷面密度σp。但球体内总的体极化电荷电量Qp体与球表面总的面极化电荷电量Qp面相等,且电性相反,即Qp体=-Qp面。由于自由电荷激发电位移矢量场,采用介质中的高斯定理,

根据各向同性介质中介质的电磁性质方程,即电位移矢量与电场强度的关系D=εE,可得球外真空中和球内介质中任意一点的电场强度为
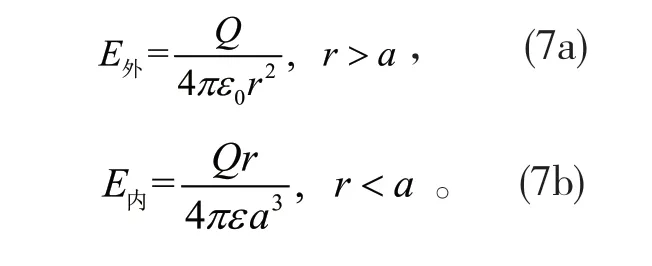
电场强度的方向仍然沿径向方向,也即只有法向分量。可以看出,由此方式求出的电场强度,在以球面为界面的两侧,电场强度的法向分量是不连续的,如图2 所示。

图2 介质中的高斯定理求出的均匀带电球体的电场
由麦克斯韦方程组中法拉第电磁感应定律的积分形式,可得法向电场的边值关系为:
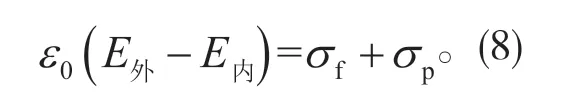
该式表示,交界面上的自由电荷面密度和极化电荷面密度是界面两侧法向电场不连续的原因。对于均匀带电球体,其自由电荷是呈体分布的,因此自由电荷面密度σf=0。
对于(8)式左边,将(7a)和(7b)式代入,可得
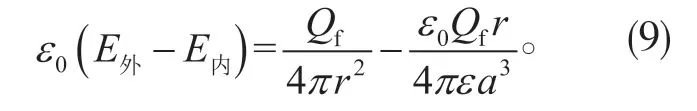
对于(8)式右边,此时只有极化电荷面密度σp。由极化电荷面密度跟界面两侧极化强度的关系,可表示为:

由于球外空间为真空,则(10)式中球外的极化强度P外=0,也即极化电荷面密度在数值上就等于介质球内的极化强度P内。进一步根据极化强度与电场强度的关系,则可得(8)式右边

与(9)式相等。这表明,采用介质中的高斯定理求得的球内外电场强度是正确的,其结果也符合电磁场的边值关系。
2 均匀带电球体激发电场的基本物理模型
从以上的分析可知,由介质中的高斯定理可以先得到辅助量电位移矢量,再由电位移矢量可得均匀带电球体内外任意一点的电场强度。事实上,直接由真空中的高斯定理也可以得到不矛盾的结果,但需要将高斯面内的电荷加以区别,如图3 所示。

图3 均匀带电球体电荷组成及电场分布物理模型
在r >a 的球外真空中,高斯定理等式右边的电荷量应为高斯面内包围的全部电荷,即:

其中,Q总=Qf+Qp体+Qp面,式中Q总表示高斯面内所包围的总电荷量,Qf表示均匀带电球上带的总自由电荷量,Qp体为球内总的体极化电荷量,Qp面则是分布在球面上的总面极化电荷量。由于Qp体=-Qp面,则Q总=Qf,这个Qf即常被描述成均匀带电球体所带电荷量Q。于是,球外的电场强度为:
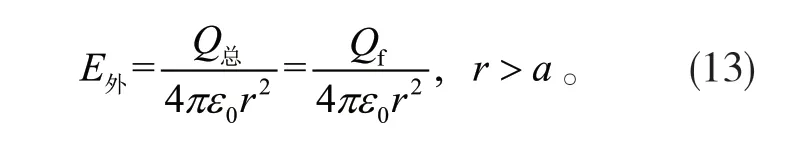
与(2a)式及(7a)式相同。
在r <a 的介质球内,高斯面内所包围的电荷为部分自由电荷和部分体极化电荷。根据极化电荷体密度ρp和自由电荷体密度ρf的关系:

可知,高斯面内包围的极化电荷比自由电荷少,但两者之比是不变的。直接运用高斯定理

将(16)式代入(15)式即可得到球内的电场强度为

此结果与(7b)式同,但与(2b)式不同,其差别在(17)式里分母中的电容率为介质的电容率ε,而(2b)式里分母中的电容率为真空电容率ε0。
由以上讨论可知,介质球所带的自由电荷Qf、球体内的极化电荷Qp体和球面极化电荷Qp面都对电场强度有贡献,在运用由电场强度表示的积分形式高斯定理时,三种电荷都是激发电场强度的源。
以一种薄膜材料二氧化铪(HfO2)为例,其相对电容率εr=ε/ε0=12.49[7]。假设该薄膜介质球半径为5cm,所带自由电荷电量为Qf=Q=1.6×10-6C,通过数值计算的仿真分析,可得不同区域的电场强度变化规律,如图4 所示。

图4 均匀带电球体内外场强分布曲线
3 结语
精确描述均匀带电球体的电场分布是静电学中既基础又重要的问题。本文对均匀带电球体内外的静电场表达式进行了严格推导与理论分析,给出了均匀带电球体激发电场的基本物理模型。得到当r >a 时,Qp体和Qp面都可以等价成一个电量相等的在球心的点电荷,但由于电性相反,两者激发的电场在球外互相抵消,其结果是球外的电场只与介质球所带的自由电荷Qf有关,该Qf即为通常描述的均匀带电球体所带的电量Q;当r <a 时,Qp面对球内电场没有贡献,或激发的电场在球内为0,同样,任意r <a 的高斯面至球面之间的球壳部分内的自由电荷和体极化电荷在r <a 的区域激发的电场也为0,但任意r <a的高斯面内的部分自由电荷和部分极化电荷激发的电场均不为0,此时运用由电场强度表示的积分形式高斯定理时,则需要把这两种电荷都考虑进来,才能得到满足电场强度边值关系的球面两侧的电场强度是不连续的结果。该研究进一步明晰了均匀带电球体激发电场的物理模型,得到了与电场法向分量连续性理论吻合的修正表达,可对大学物理、电磁学、电动力学等基础问题提供参考,也可对相关电磁软件的开发提供借鉴与佐证,后续将进一步对非均匀、各向异性等带电体激发的电场进行深入研究。

