斜槽式单激励纵扭超声变幅杆设计*

吴豪琼 高志强

(河南工学院机械工程学院 新乡 453000)

0 引言

近年来，纵扭超声加工技术在复合材料、结构陶瓷及高温合金等材料加工领域逐步得到了应用[1-3]。实现纵扭超声振动的方法按照原理可分为两类[4-8]：通过转换器类和换能器类实现。但因转换器类功率容量有限、旋转实现困难和换能器的功率有限、纵扭两向不易同频谐振等原因实现困难。

针对以上情况，本文设计了圆截面阶梯型变幅杆小端增加开斜槽圆环传振杆的变幅杆，圆截面阶梯型变幅杆有加速和聚能的作用，可增强振幅输出，同时圆环传振杆上开斜槽可获得纵扭复合振动输出，结合两者的特点并经过特殊结构改造，可实现纵扭振动输出且振幅增强。其设计过程如下：首先基于传统理论计算变幅杆尺寸，再通过单因素法仿真分析变幅杆结构尺寸对谐振频率和振型的影响规律并确定最优结构参数，最后加工出变幅杆并检测其振动参数。

1 纵扭复合变幅杆理论设计

1.1 半波长阶梯型变幅杆设计

根据一维波动理论，忽略横向振动，在简谐振动情况下，变截面变幅杆纵向振动的波动方程为[9]

式(1)中：ε为变截面杆质点位移函数，ε=ε(x)；A为杆的横截面积函数，A=A(x)；k为圆波数，k=ω/c；ω为圆频率；c为纵波在细棒中的传播速度，c=(E/ρ)1/2；E为弹性模量；ρ为变截面杆材料的密度。

图1 为阶梯型变幅杆尺寸，设大端直径为D，长度为L1，截面积为S1，小端直径d，长度L2，截面积为S2，变幅杆总长L=L1+L2，根据式(1)可确定阶梯型变幅杆纵向振动时的频率方程、放大系数Mp和位移节点x0[9-10]：

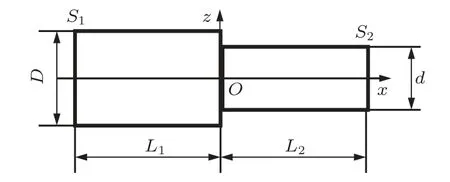
图1 阶梯型变幅杆Fig.1 Stepped horn

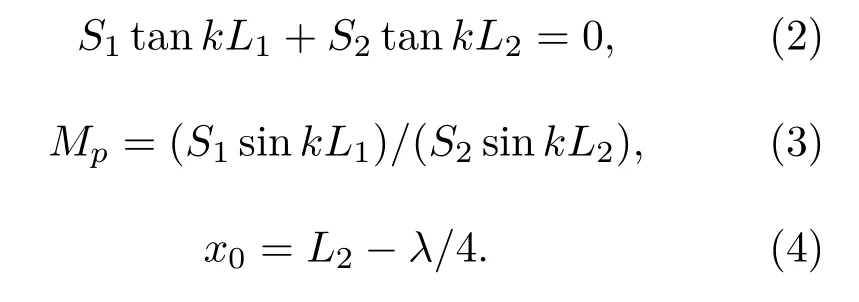
假设L1=L2=λ/4(λ为波长)，则可以推出tankL= 0，Mp=(D/d)2，x0= 0。根据一维纵向振动理论设计半波长圆截面阶梯型变幅杆[11]，材料选择45#钢，密度ρ= 7.7×103kg/m3，杨氏模量E=2.06×1011N/m2，泊松比σ=0.28，由大端D=45 mm、小端d=18 mm均匀杆组成，设定工作频率f=20 kHz可以计算得到L1=L2=65 mm。

1.2 圆环带斜槽传振杆设计

横波的质点振动方向与横波传播的方向垂直且易引起剪切变形，固体介质能承受剪切应力而液体和气体却不能，因此横波只能在固体介质中传播，却不能在液体和气体中传播[12]。所以如图2 所示，在圆环传振杆中纵波σ1以入射角β射入，以反射角β射出，反射横波τ2以反射角θ射出。反射纵波σ2和反射横波τ2都与杆的轴线成一定角度，在杆的轴向与周向上可分解出两个分量，在周向上的分量之和就能实现扭转振动。据此在阶梯变幅杆小端增加一段传振杆就能实现纵扭谐振，其结构如图3 所示：传振杆直径等于变幅杆小端直径d= 18 mm，壁厚选定h= 4；斜槽个数选定n= 6(l= 10 mm、b= 2 mm)、夹角α= 45°[6-7,12]；L3与L4可调，暂定L3=39 mm，L4=22 mm。

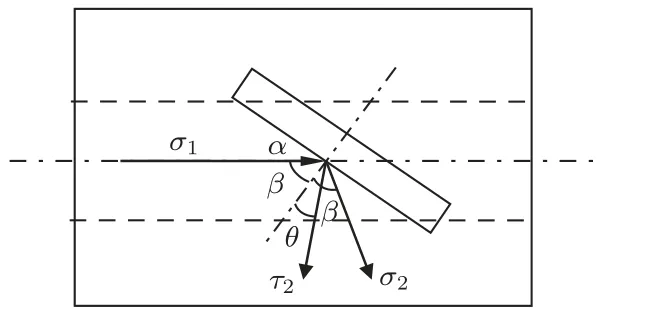
图2 传振杆扭振原理图Fig.2 The effect of the slitted configuration

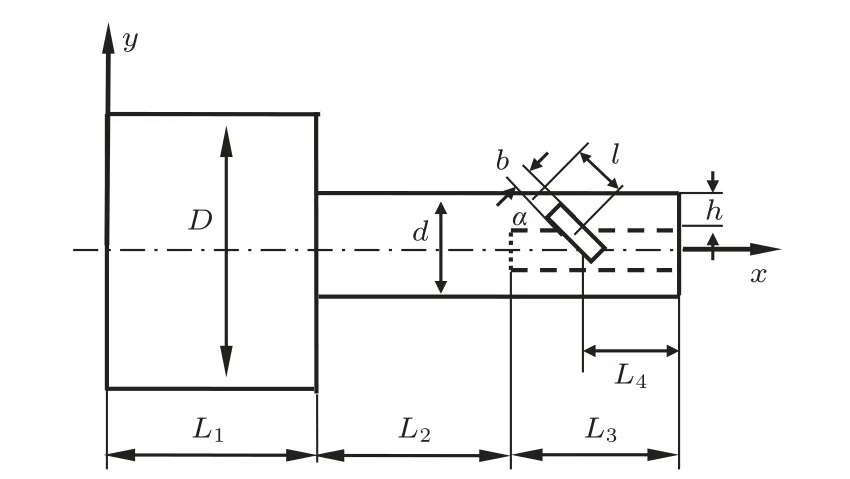
图3 斜槽圆环传振杆的阶梯型变幅杆结构Fig.3 Structural representation of stepped horn

2 纵扭复合变幅杆有限元分析优化

2.1 模态分析

为便于变幅杆装夹，在其大小端变截面处增加直径为52 mm、厚度为4 mm的法兰盘，法兰增加会导致变幅杆谐振频率和节点位置变化，变幅杆最终结构如图4 所示，其中z坐标轴轴线过两个对称方形斜槽的中心连线。使用有限元仿真软件对变幅杆进行模态分析，保持变幅杆以上的结构尺寸不变，采用单因素法分别改变L1、L2、L3和L4的尺寸，找到变幅杆20 kHz附近的纵扭谐振频率，并保证法兰盘处于变幅杆的节点位置。尺寸改变对纵扭谐振频率的变化规律如图5所示。

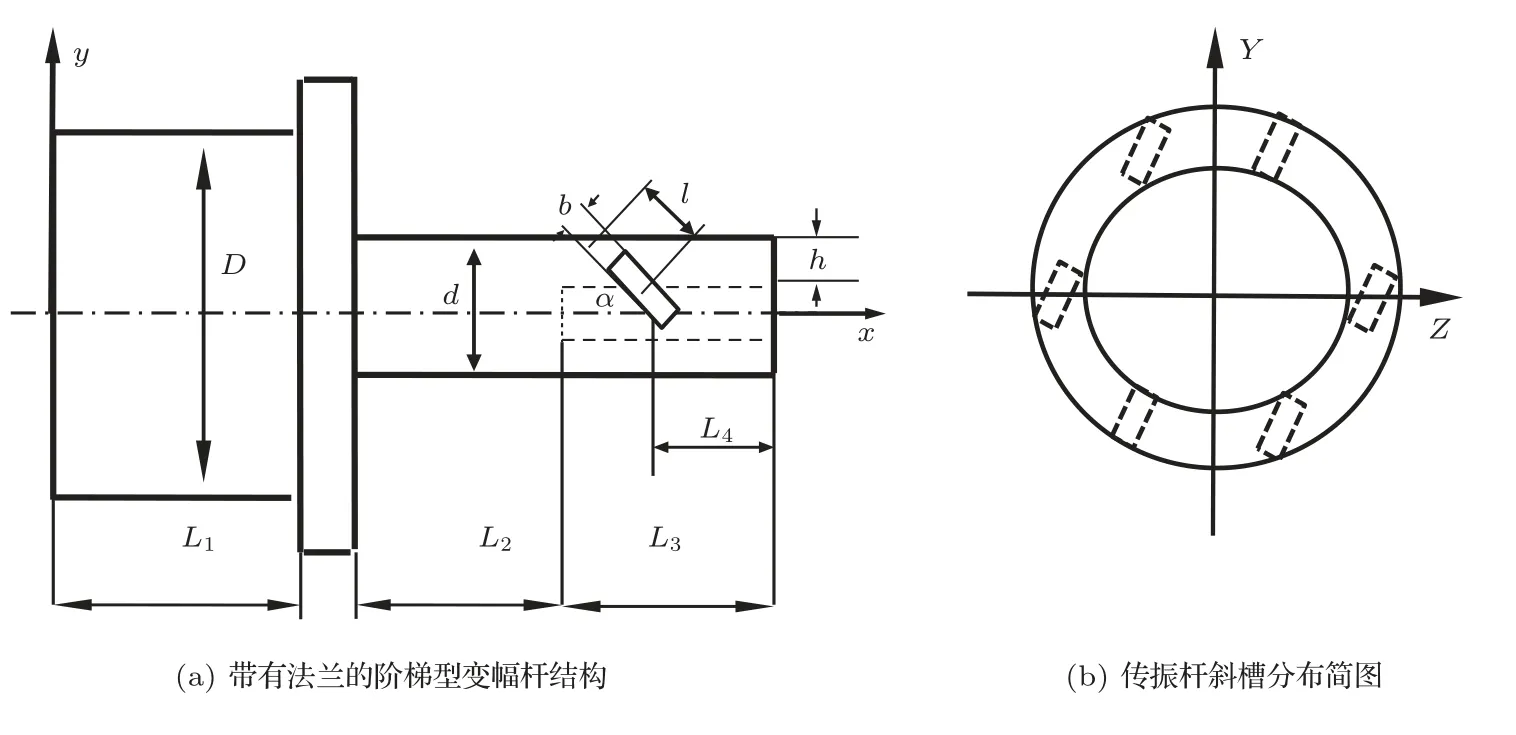
图4 阶梯型变幅杆最终结构Fig.4 Structural representation of the finally stepped horn

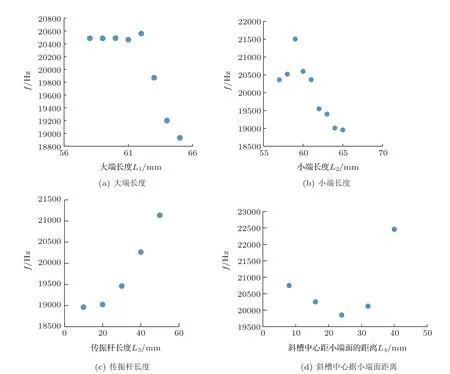
图5 单因素变幅杆结构参数对纵扭振动频率的影响Fig.5 Influence of structure size on frequency of stepped horn

由图5 谐振频率变化规律和模态仿真振型确定变幅杆最终尺寸为：变幅杆大端D= 45 mm，L1=62.75 mm；小端d=18 mm，L2=56.75 mm；传振杆L3= 30 mm，壁厚h= 4 mm；斜槽数目n= 6，倾角α= 45°，斜槽长l= 10 mm，宽b= 2 mm；斜槽中心距小端L4= 22 mm。最终尺寸模态仿真的阵型如图6 所示，在f= 19457 Hz 时纵向和扭向同时发生谐振且振型较好。

图6 变幅杆纵扭复合振动振型图Fig.6 The simulation result of stepped horn

2.2 谐响应分析

设变幅杆沿轴向接受换能器传递的纵波激励为u(x)=Asin(2πft)mm(频率f=19457 Hz，周期T0= 1/19457 s，振幅A= 5 μm)，对变幅杆进行谐响应分析，结果如图7 所示。在谐振频率f= 19457 Hz 附近输出端节点各方向振幅位移达到最大值，说明在单激励纵振条件下变幅杆可实现纵扭谐振输出。

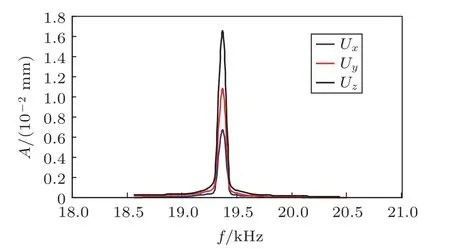
图7 变幅杆谐响应分析结果Fig.7 Harmonic response analysis

2.3 瞬态动力学分析

在变幅杆输出端端面上任选一质点，研究其运动轨迹，则可厘清端面振动特性。设定换能器纵波激励为u(x)=Asin(2πft)mm(频率f= 19457 Hz，周期T0= 1/19457 s，振幅A= 5 μm)，逐步增加瞬态分析时长(5T0、10T0、20T0)，采集输出端端面任意质点(153.5,6.8559,-2.4503)的输出振幅响应。当分析时长为20T0时，变幅杆在纵波单激励下3 个方向均有响应振幅输出：Ux和Uy方向振幅显现出周期性分布如图8(a)、图8(b)所示，从图中可以看出，输出端Ux和Uy方向振幅波动周期约为T ≈10T0重复出现，但图8(c)Uz方向振幅并未显示出T ≈10T0周期性，且与Ux和Uy方向幅值大小关系发生变化。这可能是因为瞬态动力学仿真分析时增加了外界干扰因素，受周向均匀分布斜槽的环型结构影响，或是数据采集位置不同，其原理有待进一步探讨。

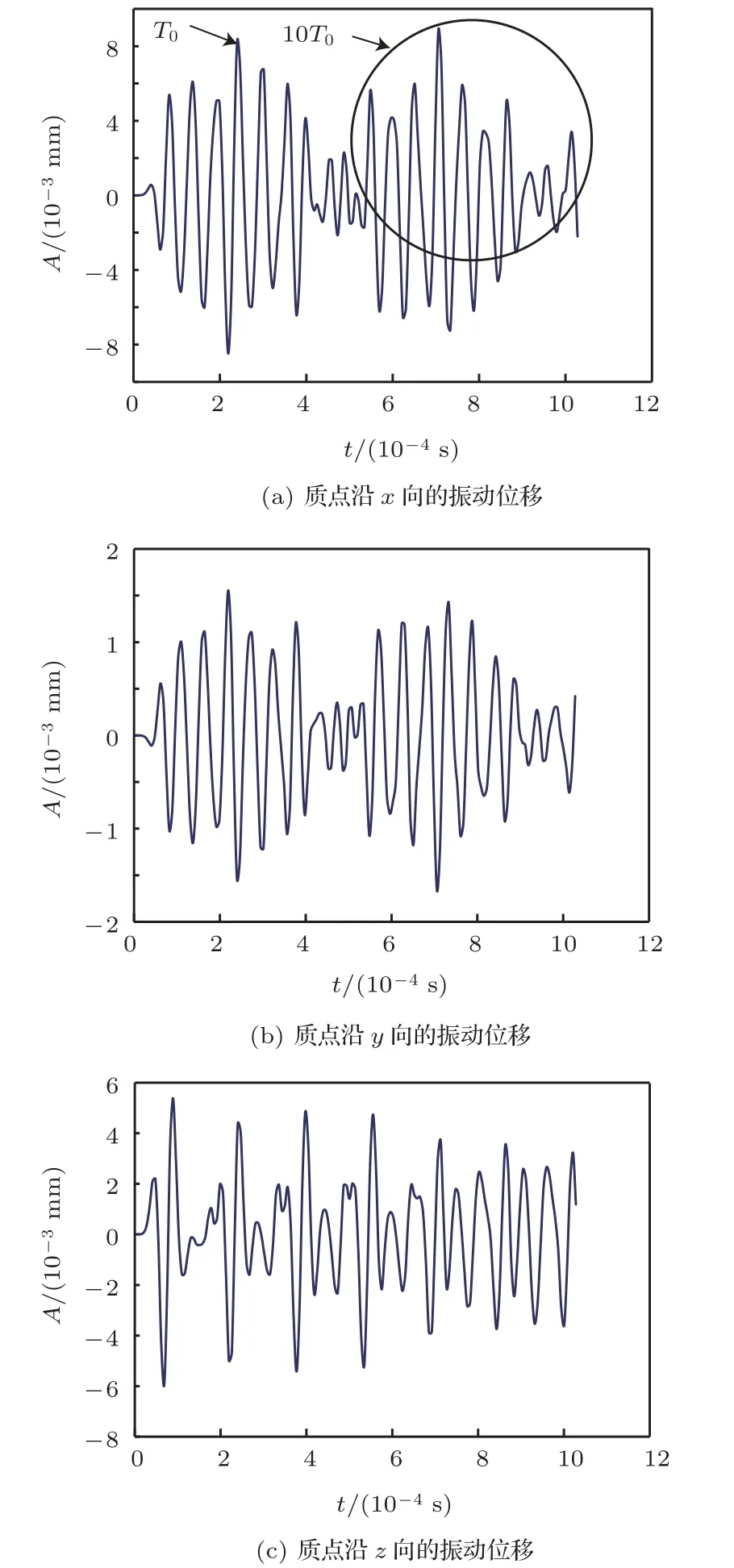
图8 变幅杆瞬态动力学分析结果Fig.8 Transient dynamic analysis

使用绘图软件对质点(153.5,9.8559,-2.4503)运动轨迹进行拟合，提取1 个周期内(特取T= 0～1/19457 s)和10 个周期内(取T= 0～10/19457 s)的所有位移数据，可获得该质点的运动轨迹曲线，如图9 所示，可知小端输出的振动轨迹为空间二维曲线。

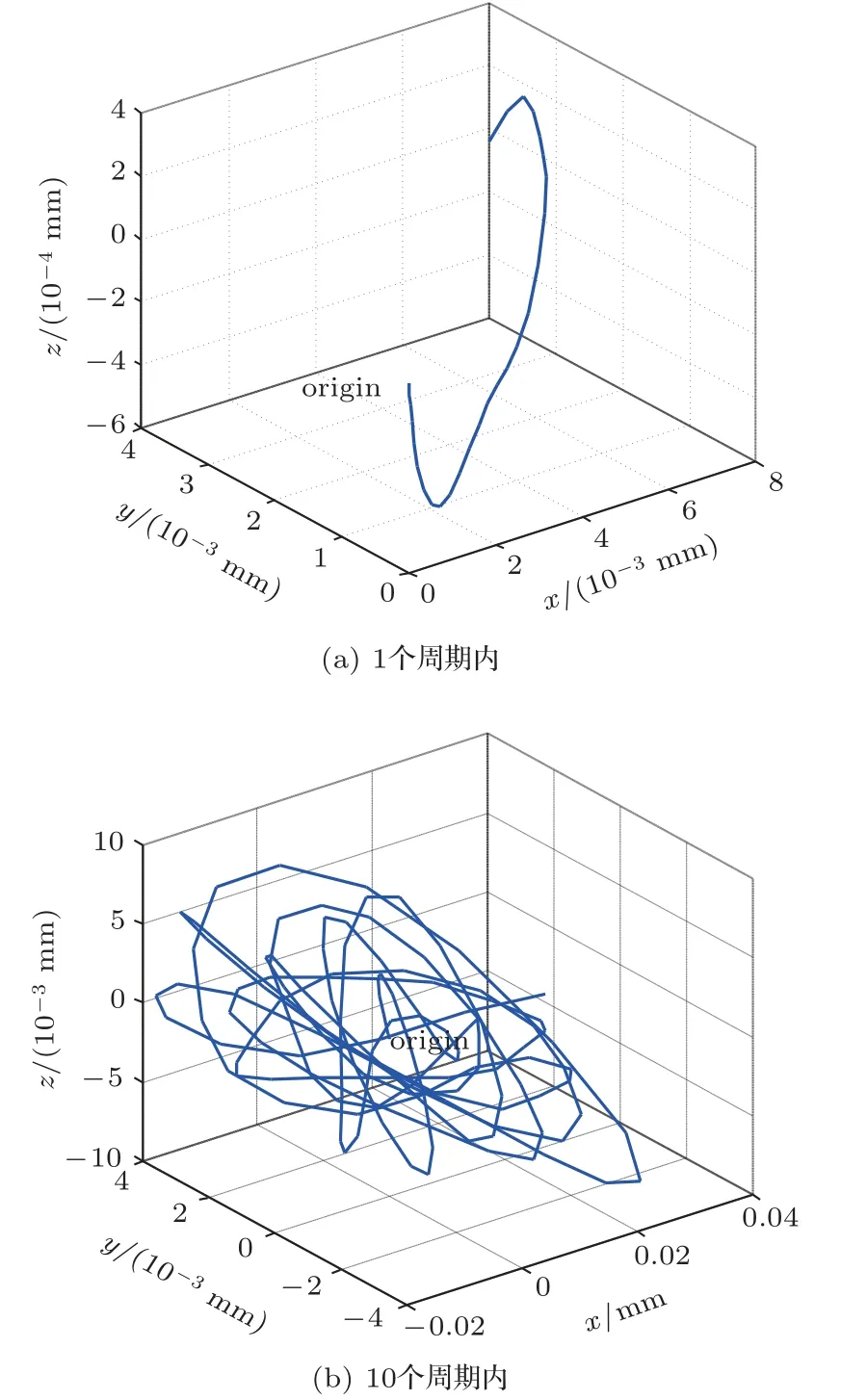
图9 输出端端面质点运动轨迹Fig.9 The displacement response curve of the point

3 复合变幅杆阻抗实验分析

根据有限元优化结果，按最终优化设计尺寸加工出变幅杆(如图10(a)所示)，使用Impedance Analyzer PV70A阻抗分析仪对其进行阻抗分析，结果如图10(b)所示。变幅杆与20 kHz 换能器的谐振频率为19884 Hz，与有限元仿真频率19457 Hz较为接近且导纳圆完整，变幅杆阻抗特性稳定。

图10 变幅杆阻抗测试Fig.10 Impedance test site

给换能器加载5 μm 的纵向20 kHz 的超声振动，使用KEYENCE 传感器、电荷放大器、数据采集卡、计算机组成的超声振动振幅测试系统对变幅杆小端圆周方向和轴向分别进行多点输出振幅测量。将KEYENCE 传感器对准变幅杆小端端面圆周上，每隔45°采集1 个点进行切向振幅测试，结果如图11(b)所示，可知切向振幅为12.7 μm；将传感器对准变幅杆小端截面进行纵向振幅测试，结果如图11(c)所示，可知纵向振幅为8.5 μm。

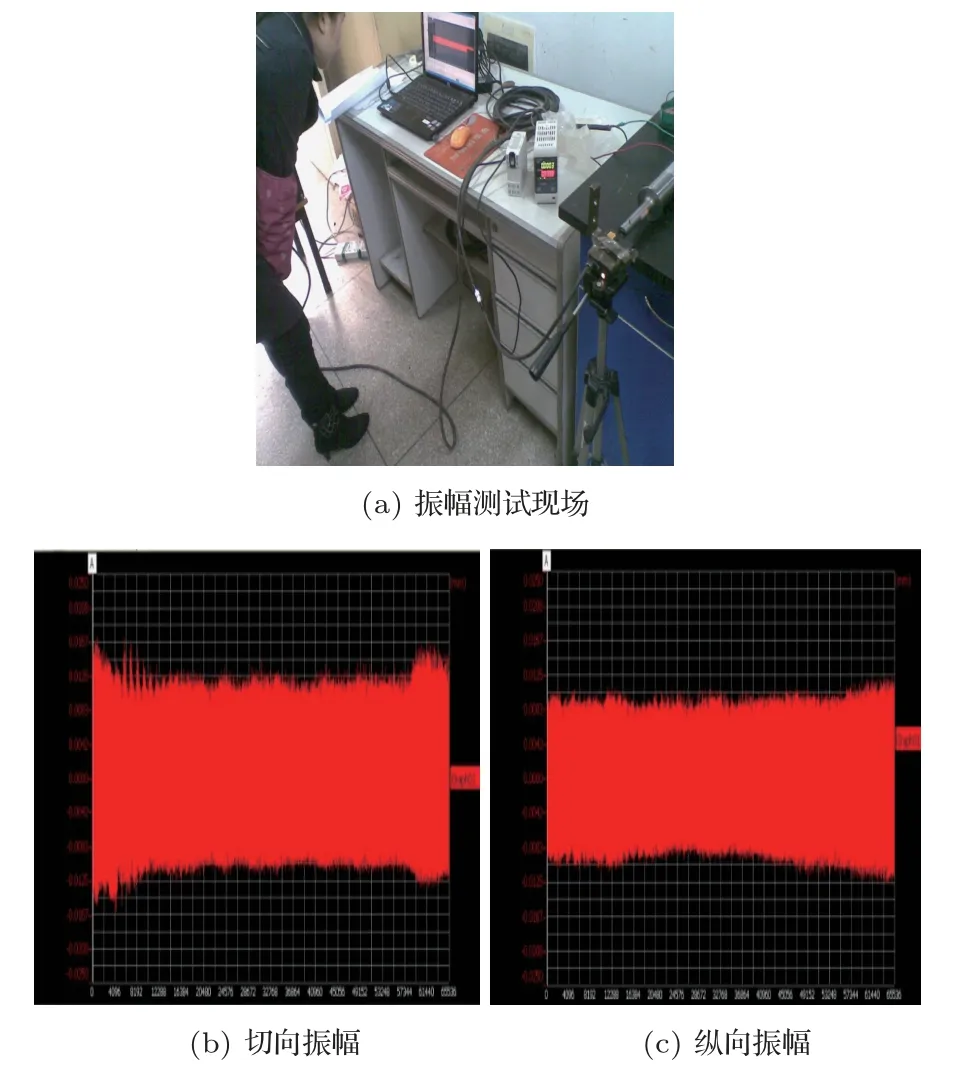
图11 变幅杆振幅测试Fig.11 Amplitude test site

4 结论

(1)本文首先通过理论计算设计，然后使用有限元分析法进行分析修正，最终得到变幅杆尺寸。该方法可作为设计纵扭声学系统的一种参考方法。仿真结果证明：变幅杆在纵波单激励振动下响应输出的振幅呈周期性，Ux和Uy方向振动周期约为激励信号周期的10倍，且输出端端面质点的运动轨迹为空间二维曲线。

(2)根据数值计算和仿真修正得到的尺寸制作变幅杆，其阻抗测试结果表明其谐振频率为19884 Hz，与仿真设计谐振频率19457 Hz 误差率仅为2.1%；输入5 μm 的纵向20 kHz 的超声振动，测试变幅杆切向振幅和纵向振幅分别为12.7 μm 和8.5 μm，证明变幅杆实现了纵扭谐振且振幅增强、振型较好。

(3)圆截面阶梯型变幅杆增加开斜槽传振杆可实现纵扭谐振，其尺寸为：大端直径D= 45 mm，长度L1= 62.75 mm；小端直径d= 18 mm，长度L2= 56.75 mm；法兰直径52 mm 厚4 mm；传振杆长L2= 30 mm，壁厚h= 4 mm；斜槽数目n= 6，斜槽与变幅杆轴线夹角α= 45°，斜槽长l×宽b为10 mm×2 mm，斜槽中心距小端面距离L4=22 mm。

本文在仿真设计过程中考虑影响变幅杆谐振频率的几何结构参数较少，而且没有总结出开斜槽传振杆阶梯型变幅杆理论设计公式，有待进一步探索研究。